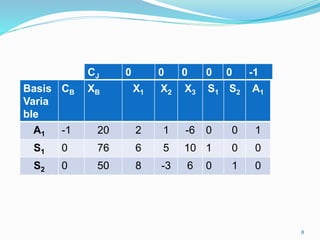
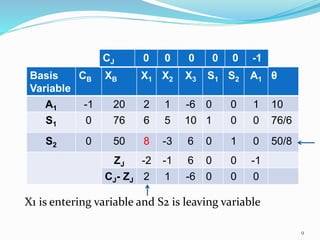
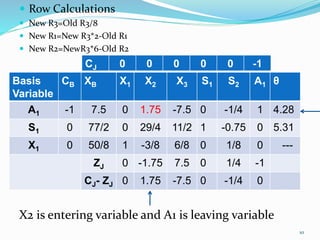
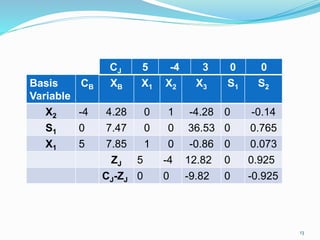
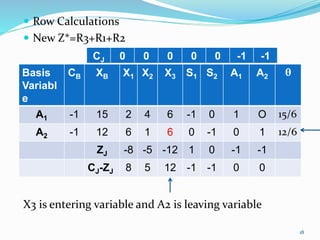
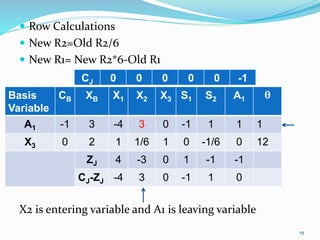
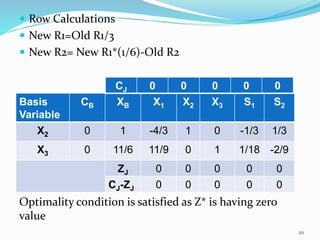
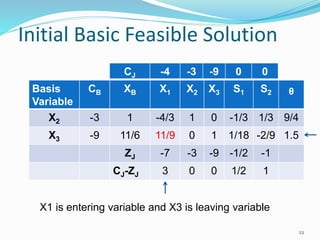
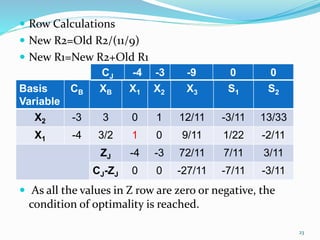
The document describes the two-phase method of linear programming, which is used to find an initial basic feasible solution (IBFS) when dealing with constraints that include slack and artificial variables. It outlines the steps involved in both phases, including the creation of an auxiliary objective function and conducting simplex method calculations. Two examples are provided to illustrate the implementation of the two-phase method in solving linear programming problems.