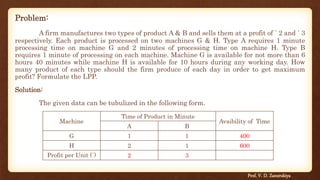
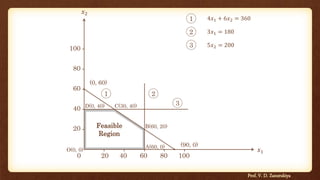
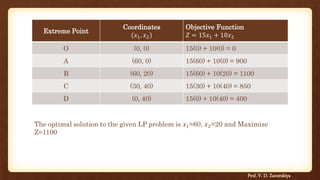
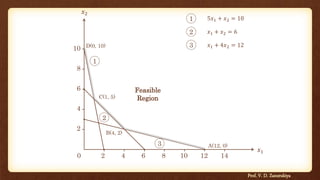
This document provides information about operation research and the graphical method for solving linear programming problems. It defines operation research and describes the general structure of a linear programming model, which includes decision variables, the objective function, and constraints. The document then formulates a sample linear programming problem and provides the step-by-step graphical solution, identifying the feasible region and finding the optimal solution that maximizes the objective function.

1. Operation Research
Graphical Method
Prof. V. D. Zanzrukiya
Department of Computer Science
Smt. C. K. Patel M.Sc.(CA & IT) College
Kadi(Gujarat) - INDIA
v.d.zanzrukiya@gmail.com

2. Definition of Operation Research
• Operation research is the application of the methods of science to
complex problems in the direction and management of large
systems of men, machines, materials and money in industry,
business, government and defence. The distinctive approach is to
develop a scientific model of the system incorporating
measurements of factors such as chance and risk, with which to
predict and compare the outcomes of alternative decisions
strategies or controls. The purpose is to help management in
determining its policy and actions scientifically.
- Operation Research Society, UK
Prof. V. D. Zanzrukiya

3. General Structure of Linear Programming Model
• The general structure of L.P. Model consists of three basis elements or
components
1. Decision variables ( Activities)
2. The objective function (OR Goal Function)
3. The Constraints
In our day to day life or in an industrial company there are certain
problems in which objectives like profit, cost, revenue, distance, time, etc. are
either to be maximized or minimized subject to certain conditions over certain
factors (variables). If such an objective as well as conditions can be written as
Linear function in terms of certain variables then such a problem is called
Linear Programming Problem.
Prof. V. D. Zanzrukiya

4. • General L.P. Model can be described as follows:
Find the values of x1, x2, …, xn so as to optimize (maximize or minimize)
Z = c1x1 + c2x2 + … + cnxn
Subject to the constraints
a11x1 + a12x2 + … + a1nxn (≤, =, ≥) b1
a21x1 + a22x2 + … + a2nxn (≤, =, ≥) b2
⋮ ⋮ ⋮ ⋮ ⋮
am1x1 + am2x2 + … + amnxn (≤, =, ≥) bm
Such that x1, x2, …, xn ≥ 0
(1) is called the objective (goal) function
(2) Represents set of constraints
(3) Represents the non-negative constraints
--- --- (1)
--- --- (2)
--- --- (3)
Prof. V. D. Zanzrukiya

5. Remarks
i. x1, x2, …, xn are called decision variables.
ii. The constants c1, c2, …, cn in the objective functions are called cost
coefficients.
iii. Constants b1, b2, …, bm in the set of constraints are called the right hand
side constants.
iv. In each and every constrains of set (2) one and only one of the relation ≤, =
or ≥ holds true. Different relations may occur in different constraints.
v. Constants ai’s in set of constraints (2) are called input-output coefficients
or technological coefficients.
Prof. V. D. Zanzrukiya

6. Formulation of LPP
Prof. V. D. Zanzrukiya

7. Problem:
A firm manufactures two types of product A & B and sells them at a profit of ` 2 and ` 3
respectively. Each product is processed on two machines G & H. Type A requires 1 minute
processing time on machine G and 2 minutes of processing time on machine H. Type B
requires 1 minute of processing on each machine. Machine G is available for not more than 6
hours 40 minutes while machine H is available for 10 hours during any working day. How
many product of each type should the firm produce of each day in order to get maximum
profit? Formulate the LPP.
Solution:
The given data can be tubulized in the following form.
Machine
Time of Product in Minute
Avaibility of Time
A B
G 1 1 400
H 2 1 600
Profit per Unit (`) 2 3
Prof. V. D. Zanzrukiya

8. Continue…
Let the firm manufacture x1 units of the product of type A and x2 units of the product
of type B.
Find x1 and x2 in order to
maximize Z = 2x1 + 3x2
Subject to the constraints
x1 + x2 ≤ 400
2x1 + x2 ≤ 600
and x1, x2 ≥ 0
Prof. V. D. Zanzrukiya

9. Linear Programming
The Graphical Method
Prof. V. D. Zanzrukiya

10. Introduction
An optimal as well as a feasible solution to an LP problem is obtained by
choosing a value from several possible values of decision variables x1, x2, …, xn ,
the one set of values that satisfies the given set of constrains simultaneously and
also provides the optimal (maximum or minimum) value of the given objective
function.
For LP problems that have only two variables, it is possible that the
entire set of feasible solutions can be displayed graphically by plotting linear
constraints on a graph paper in order to locate the best (optimal) solution. The
Technique used to identify the optimal solution is called the graphical solution
approach or technique for an LP problem with two variables.
Prof. V. D. Zanzrukiya

11. Important Definition
 Slack Variable
A non-negative variable which converts ≤ type constraint of a LPP into the equation is
called a slack variable such a variable is added to the LHS of ≤ type constraints.
Example:
2x1 + x2 ≤ 600
2x1 + x2 + S = 600
Surplus Variable
A non-negative variable which converts ≥ type constraint of a LPP into the equation is
called a surplus variable such a variable is subtracted from the LHS of ≥ type constraints.
Example:
2x1 + 3x2 ≥ 900
2x1 + 3x2 – S = 900
Slack Variable
Surplus Variable
Prof. V. D. Zanzrukiya

12.  Solution
The set of values of decision variables xj ( j = 1, 2, …, n) that satisfy the constraints of an
LP problem is said to constitute the solution to that LP problem
 Feasible Solution
The set of values of decision variables xj ( j = 1, 2, …, n) that satisfy all the constraints and
non-negativity conditions of an LP problem simultaneously is said to constitute the feasible
solution to that LP problem
 Infeasible Solution
The set of values of decision variables xj ( j = 1, 2, …, n) that do not satisfy all the
constraints and non-negativity conditions of an LP problem simultaneously is said to constitute
the infeasible solution to that LP problem
 Basic Solution
For a set of m simultaneous equations in n variables ( n > m), a solution obtained by
setting ( n – m) variables equal to zero and solving for remaining m equations in m variables is
called a basic solution.
The ( n – m) variables whose value did not appear in this solution are called non-basic
variables and the remaining m variables are called basic variables.
Prof. V. D. Zanzrukiya

13.  Basic Feasible Solution
A feasible solution to an LP problem which is also the basic solution is called the basic
feasible solution.. That is, all basic variables assume non-negative values.
Basic feasible solutions are of two types:
(a) Degenerate: A basic feasible solution is called degenerate if the value of at least
one basic variable is zero.
(b) Non-degenerate: A basic feasible solution is called non-degenerate if values of all m
basic variables are non-zero and positive.
Optimum Basic Feasible Solution
A basic feasible solution that optimizes (maximizes or minimizes) the objective
function value of the given LP problem is called an optimum basic feasible solution.
Unbounded Solution
A solution that can indefinitely increase or decrease the value of the objective function
of the LP problem is called an unbounded solution.
Prof. V. D. Zanzrukiya

14. GRAPHICAL SOLUTION METHODS OF LP PROBLEM
• Extreme Point Solution Method
In this method, the coordinates of all corner (or extreme) points of the feasible region (space or
area) are determined and then values of the objective function at these points are computed
and compared because the mathematical theory of LP states that an optimal solution to any
LP problem always lie at one of the corner (extreme) points of the feasible solution space.
The steps of the method are summarized as follows:
Step-1: Develop an LP model
Generate the mathematical model of the given LP problem.
Step-2: Plot constraints on graph paper and decide the feasible region
(a) Replace ≤ and ≥ sign to = in each constraint (inequality to equality).
(b) Find the two points of each line and draw it on graph.
Prof. V. D. Zanzrukiya

15. Continue…
(c) For inequality sign of each constraint, decide the area of feasible solution.
(For ≤ constraint it is left side of the line and for ≥ constraint it is right side of the line.
So for easy understanding, take any point of left side of line and if it satisfies the
constraint then mark the left side area otherwise mark the right side area)
(d) Shade the common portion of the graph.
Step-3: Examine extreme points of the feasible solution space to find an optimal
solution
(a) Decide the extreme points (corner points) of the feasible region.
(b) Calculate the objective function value at each extreme points.
(c) Find out min or max value (optimal value) of the objective function.
Prof. V. D. Zanzrukiya

16. Examples on Maximization LP Problem
Example: Use the graphical method to solve
the following LP problem
Maximize 𝑍 = 15𝑥1 + 10𝑥2
Subject to the constraints
4𝑥1 + 6𝑥2 ≤ 360
3𝑥1 ≤ 180
5𝑥2 ≤ 200
and 𝑥1, 𝑥2 ≥ 0
Solution:
Here Given LP problem is
Maximize 𝑍 = 15𝑥1 + 10𝑥2
Subject to the constraints
4𝑥1 + 6𝑥2 ≤ 360
3𝑥1 ≤ 180
5𝑥2 ≤ 200
and 𝑥1, 𝑥2 ≥ 0
Prof. V. D. Zanzrukiya

17. To draw a constraint
4𝑥1 + 6𝑥2 ≤ 360 --- ---(1)
Treat it as 4𝑥1 + 6𝑥2 = 360
When 𝑥1 = 0 then 𝑥2 =?
⇒ 4 0 + 6𝑥2 = 360
⇒ 6𝑥2 = 360
⇒ 𝑥2=
360
6
= 60
∴ 𝑥1, 𝑥2 = (0, 60)
When 𝑥2 = 0 then 𝑥1 =?
⇒ 4𝑥1 + 6 0 = 360
⇒ 4𝑥1 = 360
⇒ 𝑥1 =
360
4
= 90
∴ 𝑥1, 𝑥2 = (90, 0)
To draw a constraint
3𝑥1 ≤ 180 --- ---(2)
Treat it as 3𝑥1 = 180
⇒ 3𝑥1 = 180
⇒ 𝑥1 =
180
3
= 60
Here Line is parallel to Y-axis
To draw a constraint
5𝑥2 ≤ 200 --- ---(3)
Treat it as 5𝑥2 = 200
⇒ 5𝑥2 = 200
⇒ 𝑥2 =
200
5
= 40
Here Line is parallel to X-axis
Prof. V. D. Zanzrukiya

18. Prof. V. D. Zanzrukiya
𝑥1
𝑥2
0 20 40 60 80 100
100
80
60
40
20
(0, 60)
(90, 0)
1
1 4𝑥1 + 6𝑥2 = 360
2
2 3𝑥1 = 180
3
3
5𝑥2 = 200
Feasible
Region
O(0, 0)
A(60, 0)
B(60, 20)
C(30, 40)D(0, 40)

19. Extreme Point
Coordinates
𝑥1, 𝑥2
Objective Function
𝑍 = 15𝑥1 + 10𝑥2
O (0, 0) 15(0) + 10(0) = 0
A (60, 0) 15(60) + 10(0) = 900
B (60, 20) 15(60) + 10(20) = 1100
C (30, 40) 15(30) + 10(40) = 850
D (0, 40) 15(0) + 10(40) = 400
Prof. V. D. Zanzrukiya
The optimal solution to the given LP problem is 𝑥1=60, 𝑥2=20 and Maximize
Z=1100

20. Examples on Minimization LP Problem
Example: Use the graphical method to solve
the following LP problem
Minimize 𝑍 = 3𝑥1 + 2𝑥2
Subject to the constraints
5𝑥1 + 𝑥2 ≥ 10
𝑥1 + 𝑥2 ≥ 6
𝑥1 + 4𝑥2 ≥ 12
and 𝑥1, 𝑥2 ≥ 0
Solution:
Here Given LP problem is
Minimize 𝑍 = 3𝑥1 + 2𝑥2
Subject to the constraints
5𝑥1 + 𝑥2 ≥ 10
𝑥1 + 𝑥2 ≥ 6
𝑥1 + 4𝑥2 ≥ 12
and 𝑥1, 𝑥2 ≥ 0
Prof. V. D. Zanzrukiya

21. To draw a constraint
5𝑥1 + 𝑥2 ≥ 10 --- ---(1)
Treat it as 5𝑥1 + 𝑥2 = 10
When 𝑥1 = 0 then 𝑥2 =?
⇒ 5 0 + 𝑥2 = 10
⇒ 0 + 𝑥2 = 10
⇒ 𝑥2 = 10
∴ 𝑥1, 𝑥2 = (0, 10)
When 𝑥2 = 0 then 𝑥1 =?
⇒ 5𝑥1 + 0 = 10
⇒ 𝑥1 =
10
5
= 2
∴ 𝑥1, 𝑥2 = (2, 0)
To draw a constraint
𝑥1 + 4𝑥2 ≥ 12 --- ---(3)
Treat it as 𝑥1 + 4𝑥2 = 12
When 𝑥1 = 0 then 𝑥2 =?
⇒ 0 + 4𝑥2 = 12
⇒ 4𝑥2 = 12
⇒ 𝑥2 =
12
4
= 3
∴ 𝑥1, 𝑥2 = (0, 3)
When 𝑥2 = 0 then 𝑥1 =?
⇒ 𝑥1 + 4(0) = 12
⇒ 𝑥1 + 0 = 12
⇒ 𝑥1 = 12
∴ 𝑥1, 𝑥2 = (12, 0)
Prof. V. D. Zanzrukiya
To draw a constraint
𝑥1 + 𝑥2 ≥ 6 --- ---(2)
Treat it as 𝑥1 + 𝑥2 = 6
When 𝑥1 = 0 then 𝑥2 =?
⇒ 0 + 𝑥2 = 6
⇒ 𝑥2 = 6
∴ 𝑥1, 𝑥2 = (0, 6)
When 𝑥2 = 0 then 𝑥1 =?
⇒ 𝑥1 + 0 = 6
⇒ 𝑥1 = 6
∴ 𝑥1, 𝑥2 = (6, 0)

22. Prof. V. D. Zanzrukiya
𝑥1
𝑥2
0 2 4 6 8 10 12 14
10
8
6
4
2
1
1 5𝑥1 + 𝑥2 = 10
2
2 𝑥1 + 𝑥2 = 6
3
3
𝑥1 + 4𝑥2 = 12
A(12, 0)
B(4, 2)
C(1, 5)
D(0, 10)
Feasible
Region

23. Extreme Point
Coordinates
𝑥1, 𝑥2
Objective Function
𝑍 = 𝟑𝑥1 + 𝟐𝑥2
A (12, 0) 3(12) + 2(0) = 36
B (4, 2) 3(4) + 2(2) = 16
C (1, 5) 3(1) + 2(5) = 13
D (0, 10) 3(0) + 2(10) = 20
Prof. V. D. Zanzrukiya
The optimal solution to the given LP problem is 𝑥1=1, 𝑥2=5 and Minimize Z = 13

24. Examples on Mixed Constraints LP Problem
Example: Use the graphical method to solve
the following LP problem
Maximize 𝑍 = 2𝑥1 + 3𝑥2
Subject to the constraints
𝑥1 + 𝑥2 ≤ 30
𝑥2 ≥3
0 ≤ 𝑥2 ≤ 12
0 ≤ 𝑥1 ≤ 20
𝑥1 − 𝑥2 ≥ 0
and 𝑥1, 𝑥2 ≥ 0
Solution:
Here Given LP problem is
Maximize 𝑍 = 2𝑥1 + 3𝑥2
Subject to the constraints
𝑥1 + 𝑥2 ≤ 30
𝑥2 ≥3
0 ≤ 𝑥2 ≤ 12
0 ≤ 𝑥1 ≤ 20
𝑥1 − 𝑥2 ≥ 0
and 𝑥1, 𝑥2 ≥ 0
Prof. V. D. Zanzrukiya

25. To draw a constraint
𝑥1 + 𝑥2 ≤ 30 --- ---(1)
Treat it as 𝑥1 + 𝑥2 = 30
When 𝑥1 = 0 then 𝑥2 =?
⇒ 0 + 𝑥2 = 30
⇒ 𝑥2 = 30
∴ 𝑥1, 𝑥2 = (0, 30)
When 𝑥2 = 0 then 𝑥1 =?
⇒ 𝑥1 + 0 = 30
⇒ 𝑥1 = 30
∴ 𝑥1, 𝑥2 = (30, 0)
To draw a constraint
𝑥1 − 𝑥2 ≥0 --- ---(5)
Treat it as 𝑥1 − 𝑥2 = 0
⇒ 𝑥1 = 𝑥2
When 𝑥1 = 0 then 𝑥2 =?
⇒ 𝑥2 = 0
∴ 𝑥1, 𝑥2 = (0, 0)
When 𝑥2 = 25 then 𝑥1 =?
⇒ 𝑥1 = 25
∴ 𝑥1, 𝑥2 = (25, 25)
Prof. V. D. Zanzrukiya
To draw a constraint
𝑥2 ≥ 3 --- ---(2)
Treat it as 𝑥2 = 3
Here Line is parallel to X-axis
To draw a constraint
0 ≤ 𝑥2 ≤ 12 --- ---(3)
Treat it as 𝑥2 = 12
Here Line is parallel to X-axis
To draw a constraint
0 ≤ 𝑥1 ≤ 20 --- ---(4)
Treat it as 𝑥1 = 20
Here Line is parallel to Y-axis

26. Prof. V. D. Zanzrukiya
𝑥1
𝑥2
0 5 10 15 20 25 30 35
30
25
20
15
10
5
1
1 𝑥1 + 𝑥2 = 30
2
2 𝑥2 = 3
3
3 𝑥2 = 12
4
4 𝑥1 = 20
5
5 𝑥1 − 𝑥2 = 0
Feasible
Region
A(3, 3) B(20, 3)
C(20, 10)
D(18, 12)E(12, 12)

27. Extreme Point
Coordinates
𝑥1, 𝑥2
Objective Function
𝑍 = 𝟐𝑥1 + 𝟑𝑥2
A (3, 3) 2(3) + 3(3) = 15
B (20, 3) 2(20) + 3(3) = 49
C (20, 10) 2(20) + 3(10) = 70
D (18, 12) 2(18) + 3(12) = 72
E (12, 12) 2(12) + 3(12) = 60
Prof. V. D. Zanzrukiya
The optimal solution to the given LP problem is 𝑥1=18, 𝑥2=12 and Maximize Z = 72