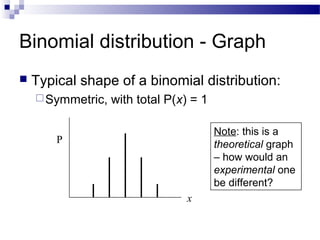
The document discusses binomial and hypergeometric distributions. It defines binomial distributions as involving independent Bernoulli trials where the probability of success is the same for each trial. The binomial probability mass function is provided. An example calculates the probability of various outcomes of coin flips. Hypergeometric distributions differ in that trials are not independent since sampling is without replacement from a finite population. The hypergeometric probability mass function is also provided.

1. Discrete Random Variables:
The Binomial Distribution

2. Bernoulli’s trials
 J. Bernoulli (1654-1705) analyzed the idea
of repeated independent trials for discrete
random variables that had two possible
outcomes: success or failure
 In his notation he wrote that the probability
of success is denoted by p and the
probability of failure is denoted by q or 1-p

3. Binomial distribution
 The binomial distribution is just n
independent individual (Bernoulli) trials
added up.
 It is the number of “successes” in n trials.
 The sum of the probabilities of all the
independent trials totals 1.
 We can define a ‘success’ as a ‘1’, and a
failure as a ‘0’.

4. Binomial distribution
 “x” is a binomial distribution if its probability function is:
 Examples (note – success/failure could be switched!):



−
=
p
p
x
10
1 probability
of success
probability
of failure
Situation x=1
(success)
x=0
(failure)
Coin toss to get
heads
Turns up heads Turns up tails
Rolling dice to get 1 Lands on 1 Lands on anything
but 1
While testing a
product, how many
are found defective
Product is defective Product is not
defective

5. Binomial distribution
 The binomial distribution is just n
independent ‘Bernoulli trials’ added up
It requires that the trials be done “with
replacement” ex. testing bulbs for defects:
•Let’s say you make many light bulbs
•Pick one at random, test for defect, put it back
•Repeat several times
•If there are many light bulbs, you do not have to
replace (it won’t make a significant difference)
•The result will be the binomial probability of a
defective bulb (#defective total sample).÷

6. Binomial distribution - formula
 Let’s figure out a binomial random
variable’s probability function or formula
 Suppose we are looking at a binomial with
n=3 (ex. 3 coin flips; ‘heads’ is a ‘success’)
 We will start with ‘all tails’ P(x=0):
Can happen only one way: 000
Which is: (1-p)(1-p)(1-p)
Simplified: (1-p)3

7. Binomial distribution - formula
 Let’s figure out a binomial probability
function (for n = 3)
 This time we want 1 success plus 2
failures (ex. 1 heads + 2 tails, or P(x=1)):
 This can happen three ways: 100, 010, 001
 Which is: p(1-p)(1-p)+(1-p)p(1-p)+(1-p)(1-p)p
 Simplified: 3p(1-p)2

8. Binomial distribution - formula
 Let’s figure out a binomial probability
function (for n = 3)
 We want 2 ‘successes’ P(x=2):
 Can happen three ways: 110, 011, 101, or…
 pp(1-p)+(1-p)pp+p(1-p)p, which simplifies to..
 3p2
(1-p)

9. Binomial distribution - formula
 Let’s figure out a binomial probability
function (n = 3)
 We want all 3 ‘successes’ P(x=3):
 This can happen only one way: 111
 Which we represent as: ppp
 Which simplifies to: p3

10. Binomial distribution - formula
 Let’s figure out a binomial probability
function – in summary, for n = 3, we have:
P(x)
(Where x is the number of successes; ex. # of heads)
( )
( )
( )







−
−
−
=
3
2
2
3
3
132
131
10
p
pp
pp
p
x
The sum of these
expressions is the
binomial distribution
for n=3. The resulting
equation is an
example of the
Binomial Theorem.

11. Binomial distribution - formula
 A quick review of the Binomial Theorem:
 If we use q for (1 – p), then…
 p3
+ 3p2
q +3pq2
+ q3
= (p + q)3
 which is an example of the formula:
(a + b)n
= ____________________
(if you forget it, check it in your text)

12. Binomial distribution - formula
 Let’s figure out a binomial r.v.’s probability
function (the quick way to compute the
sum of the terms on the previous slide) -
now here’s the formula…
In general, for a binomial:
( ) ( ) ( ) xnx
ppxP
−
−= 1nscombinatioof#
(the # of x successes with probability p in n trials)

13. Binomial distribution - formula
 Which can be written as:
( )
( )
( ) xnx
pp
xnx
n
xP
−
−
−
= 1
!!
!
or P(x) = nCx px
(1 – p)n-x
 This formula is often called the general
term of the binomial distribution.

14. Expected Value
 The expected value of a binomial distribu-
tion equals the probability of success (p)
for n trials:
( ) npXE =
 E(X) also equals the sum of the
probabilities in the binomial distribution.

15. Binomial distribution - Graph
 Typical shape of a binomial distribution:
Symmetric, with total P(x) = 1
x
P
Note: this is a
theoretical graph
– how would an
experimental one
be different?

16. Binomial distribution - example
 A realtor claims that he ‘closes the deal’
on a house sale 40% of the time.
 This month, he closed 1 out of 10 deals.
 How likely is his claim of 40% if he only
completed 1/10 of his deals this month?

17. Binomial distribution - example
 By using the binomial distribution function,
it’s possible to check if his assessment of
his abilities (i.e. 40% ‘closes’) is likely:
( )
( )
( ) ( ) ( )( )
( )
( )
( )( ) ( )( )
( )
( )
( ) ( ) ( )( )( )
( )( )
( )( ) 251.00467.00256.0
234
78910
6.04.0
!6!4
!10
4
040.0010.04.0106.04.0
!9!1
!10
1
006.0006.0116.04.0
!10!0
!10
0
64
9
100
===
===
===
P
P
PP(0 deals)=

18. Binomial distribution - example
 So it seems pretty unlikely that his assess-
ment of his abilities is right:
The probability of closing 1 or fewer
deals out of 10 if (as he claims) he
closes deals 40% of the time is less
than 5% or less than 1/20.
 What % of ‘closes’ do you think would
have the highest probability in this
distribution, if his claim was right?

19. Binomial distribution - example
 Now see if you can determine the
expected number of closings if he had 12
deals this month, assuming 40% success.
 We need the values of n (= ___) and
of p (= ____).
 E(X) = np = ______ - this means that we
would expect him to close about _____
deals, if his claim is correct. [End of first example.]

20. Binomial Distribution – ex. 2
 Alex Rios has a batting average of 0.310
for the season. In last night’s game, he
had 4 at bats. What are the chances he
had 2 hits?
 You try this one! First ask 3 questions…

21. Binomial Distribution – ex. 2
 Is each time at bat an independent event?
 Is ‘getting a hit’ a discrete random variable?
 Is this a Bernoulli trial? How would you
define a “success” and a “failure”?
 If you can answer ‘yes’ to the three
questions above, then you can use the
binomial distribution formula to answer
the problem.

22. Binomial Distribution – ex. 2
 First determine the following values:
The number of trials (Alex is at bat __ times) –
this is the value of n
The probability of success (Alex’s average is
___) – this is p
The probability of ‘failure’: 1 – p = ___
The # of successes asked for (his chances of
getting ___ hits) – this is x
 Now you can use the formula:

23. Binomial Distribution – ex. 2
( )
( )
( ) xnx
pp
xnx
n
xP
−
−
−
= 1
!!
!
 Put in the values from the previous
screen, and discuss your answers. [pause here]
 Did you get P(2) = 0.275?
 Is 2 the most likely number of hits
for Alex last night? How about 1 or 3?
 P(0 or 1 or 2 or 3 or 4 hits) = _____?

24. Hypergeometric distribution
 What happens if you have a situation in
which the trials are not independent (this
most often happens due to not replacing a
selected item).
 Each trial must result in success or failure,
but the probability of success changes
with each trial.

25. Hypergeometric distribution
 Consider taking a sample from a
population, and testing each member of
the sample for defects.
 Do this sampling without replacement.
 As long as the sample is small compared
to the population, this is close to binomial.
 But if the sample is large compared to the
population, this is a hypergeometric dist.

26. Hypergeometric dist. - formula
 A hypergeometric distribution differs from
binomial ones since it has dependent
trials.
 Probability of x successes in r dependent
trials, with number of successes a out of
a total of n possible outcomes:
rn
xranx
C
CC
xP
−−×
=
a
)(

27. Hypergeometric dist. - formula
 Expected Value – the average probability of a
success is the ratio of success overall (a/n)
times r trials:
( )
n
ra
XE =
( )
( )
( )
( ) ( )
( ) 





−






+−−−
−






−
=
!!
!
!!
!
!!
!
rnr
n
xranxn
an
xax
a
xP
 The full version of this formula is: