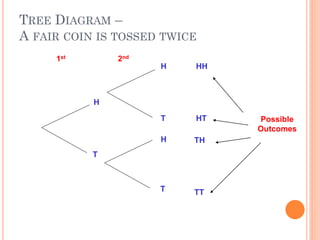
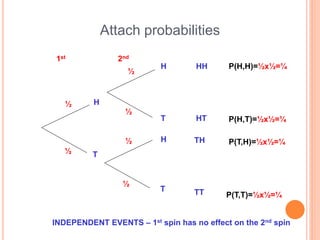
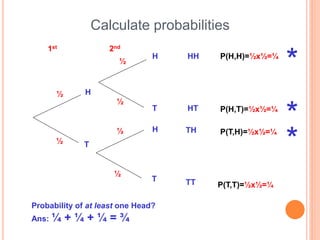
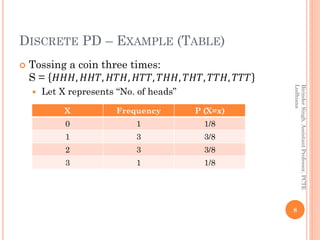
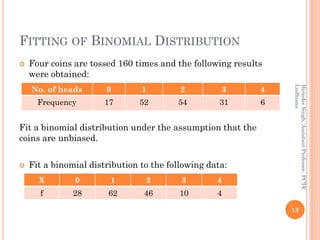
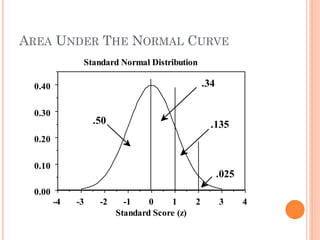
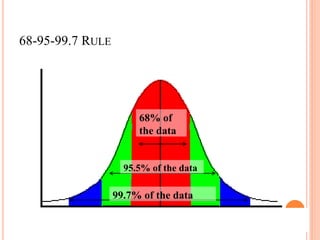
This document discusses different probability distributions including binomial, Poisson, and normal distributions. It provides examples and formulas for each distribution. The binomial distribution describes phenomena with two possible outcomes, like coin tosses. The Poisson distribution applies when there are many trials with low probability of success. The normal distribution is a continuous distribution that is symmetric and bell-shaped, commonly used to model natural phenomena.