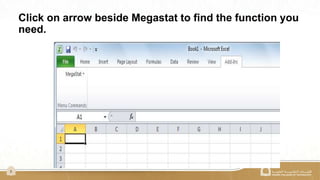
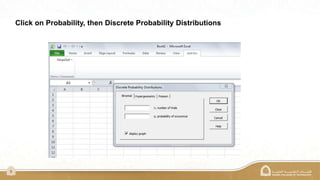
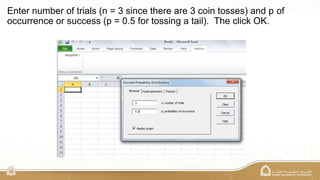
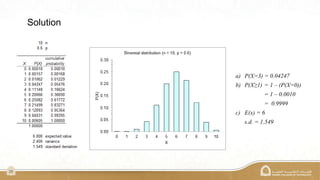
The document explains the binomial distribution, a discrete probability distribution resulting from experiments with a finite number of trials, each having two possible outcomes. It details the necessary parameters for calculating probabilities, including the number of trials and the probabilities of success and failure, as well as using Excel's MegaStat for computations. Several examples illustrate how to calculate probabilities and expected values in different scenarios involving binomial experiments.

1. Binomial Distribution
CIS 2003

2. 2
The Binomial Distribution
The Binomial distribution is a special type of discrete probability distribution
that results from a probability experiment with a limited number of "trials", in
which any trial has only two possible outcomes.
For example,
• The probability of getting a “head” when tossing a coin is 0.5. If you toss 8
coins, what is the probability that you get 3 heads or less?
Trials = 8 Outcomes = Head (0.5), Tail (0.5)
• The probability that a light bulb is “satisfactory” is 0.8. If you select 20 light
bulbs, what is the probability that at least 15 of them are satisfactory?
Trials = 20 Outcomes = Satisfactory (0.8), Not Satisfactory (0.2)

3. 3
In a Binomial distribution, we need to know the following:
n the number of trials
p the probability of “success” of one trial
q the probability of “failure” of one trial (1-p)
x the number of successes in the n trials
nCx the number of ways that x successes can occur in n trials
)!
(
!
!
x
n
x
n
Cx
n


(most scientific
calculators include a
function called nCx)
The Binomial Distribution

4. 4
Then, the probability of x successes in n trials is given by the formula
x
n
x
x
n q
p
C
x
P 



)
(
A binomial distribution can then be created using the list of all P(x) values,
from x = 0 to x = n. (Here p is the probability of success and q is the
probability of failure.)
The mean (expected value) of a binomial distribution is
calculated by: 𝜇 = 𝑛. 𝑝
The standard deviation of a binomial distribution is
calculated by: 𝜎 = 𝑛. 𝑝. 𝑞
The Binomial Distribution

5. 5
For example, an experiment is conducted in which 8 coins are tossed, and
the number of heads that appear is recorded.
In this case,
n = 8
p = 0.5
q = 0.5
We can use Megastat- Excel to give us the probability distribution with the
individual probabilities for each outcome (x = 0, x = 1, … x = 8)
The Binomial Distribution

6. 6
Using Megastat for Binomial Distribution problems
Instead of using the formula, one can use the Megastat Addin on Excel
to analyse the data.
All we need is the number of trials (n) and the probability (p) of the
successful event.
This also calculates the mean (µ), variance (σ2)
and standard deviation (σ) of the distribution.

7. 7
Using Megastat for Binomial Distribution
A coin is tossed 3 times.
What is the binomial distribution for number of tails that will result?
For Megastat, we must know the number of trials (n) and the probability of success (p).
3 coins are tossed so n = 3.
P(tossing a tail) = 0.5
To start Megastat:
1) Open a new excel file.
2) Open Megastat and click Enable Macros.
3) Then click Add-ins to access Megastat on your excel sheet.

8. 8
Click on arrow beside Megastat to find the function you
need.

9. 9
Click on Probability, then Discrete Probability Distributions to get the box below.

10. 10
Enter number of trials (n = 3 since there are 3 coin tosses) and p of
occurrence or success (p = 0.5 for tossing a tail). The click OK.

11. 11
The output produced from Excel is
shown here.
The values of X, P(X) mean, variance
and standard deviation for the
distribution are thus obtained. Note
that
µ = 1.50 (expected value)
σ2 = 0.75
σ = 0.866
Look at the table to find the
probability of tossing two tails.
P(2 tails) = 0.375

12. 12
What is the probability
of tossing at most 1 tail?
P(1) + P (0) = 0.37500 +
0.12500 = 0.50000
Or
Cumulative probability
from the table.
P(1 or less) = 0.50000

13. 13
What is the probability
of tossing at least 1 tail?
Either:
P(1) + P(2) + P(3)
= 0.87500
Or 1 – P(0)
= 1 – 0.12500
= 0.87500

14. 14
Another Example
During a study by Health officials, it was found that 4 out of 25
restaurants in a city have unsatisfactory sanitary conditions.
If a customer eats 6 times from restaurants in the city this month, how
likely the customer will experience unsatisfactory conditions?
Is this a binomial experiment?
If it is binomial, create the binomial distribution.

15. 15
Is it a binomial experiment?
1) Fixed number of trials?
2) Two outcomes only?
3) Outcomes are
independent?
4) Probability is constant for
each trial?
Yes. You will go out 6 times.
Yes. Sanitary or unsanitary.
Yes. The sanitary conditions at one
restaurant do not affect those at
another restaurant.
The probability is always 4/25.
It is a binomial experiment.

16. 16
We need to know n and p.
The number of trials (n) = 6.
P(unsanitary conditions) = 4/25 = 0.16

17. 17
1) What is the probability of eating at 2 restaurants that have unsanitary
conditions?
P = 0.19118
2) What is the probability of eating at more than 4 restaurants that have
unsanitary conditions?
p(5) + p(6) = 0.00053 + 0.00002 = 0.00055

18. 18
1) What is the probability of eating in at least 1 restaurant that has unsanitary
conditions?
You can add up all of the probabilities of P(1) to P(6).
0.40148 + 0.19118 + 0.04855 + 0.00694 + 0.00053 + 0.00002
Or Take 1 – P(0) = 1 – 0.35130
= 0.6487

19. 19
1) What is the probability of eating in at most 2 restaurants that have unsanitary
conditions?
P(2) + P(1) + P(0) = 0.019118 + 0.40148 + 0.35130
= 0.94396
or use cumulative probability from the chart.
= p(2 or less) = 0.94396

20. 20
1) What is the most likely number of times you will experience unsanitary conditions in
the month?
expected value or µ = 0.960 times
2) How variable will the data be around that number?
sd = 0.898

21. 21
Example 3
The probability that a person shopping in Al Jimi mall will take
advantage of a special promotion on ice cream is 0.30.
Suppose 6 shoppers are selected at random.
a) What is the probability that exactly 4 of these shoppers will
take advantage of this promotion?
n = 6
x = 4 Using formula
p = 0.3
q = 0.7
0595
.
0
7
.
0
3
.
0
)
4
(
)
(
2
4
4
6 






 
C
x
P
q
p
C
x
P x
n
x
x
n

22. 22
b) What is the probability that at least 5 shoppers will take
advantage of this promotion?
n = 6
x = 0, 1, 2, 3, 4, 5
p = 0.3
f = 0.7
c) What is the expected value (mean) and standard deviation?
8
.
1
)
3
.
0
)(
6
( 

 np

12
.
1
)
7
.
0
)(
3
.
0
)(
6
( 

 npq


23. 23
Using Megastat,
You can then use basic Excel functions
to calculate probability questions …
For example, to calculate P(X ≥ 6), use
=sum(C15:C19) = 0.96721

24. 24
Example 4
The phone lines to the AAWC computer help desk are free only
60% of the time. Suppose that you plan to call the help desk 10
times today.
Use Megastat to answer the following questions:
a) What is the probability that the line will be free for exactly 3 of
your calls?
b) What is the probability that the line will be free for at least 1 of
your calls?
c) What is the mean and standard deviation for the number of
times you can “expect” to get a free line?

25. 25
Solution
a) P(X=3) = 0.04247
b) P(X≥1) = 1 – (P(X=0))
= 1 – 0.0010
= 0.9999
c) E(x) = 6
s.d. = 1.549