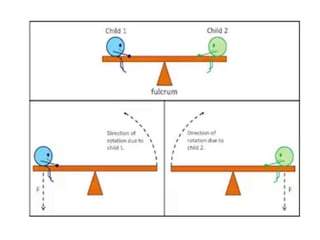
Torque is a vector quantity that measures the force causing an object to rotate around an axis, with applications in everyday life such as turning a doorknob or using a wrench. It can be classified as static, which does not produce angular acceleration, or dynamic, which does, and is mathematically expressed as τ = r x f = r . f sinθ. The net torque acting on an object is crucial for understanding rotational equilibrium, where individual torques cancel each other out.

1. Torque

2. ->Just as a linear force causes an object
to accelerate in linear kinematics
,torque causes an object to acquire
angular acceleration
->Torque is a measure of the force that
can cause an object to rotate about an
axis.

3. Torque is a vector quantity. The
direction of the torque vector
depends on the direction of the
force on the axis.

4. Torque in Everyday life
Since in simple terms torque is defined as the
twisting force that tends to cause rotation.
It is a general physics term which has many day-
to-day applications:-
-> Turning the Key ;
-> Turning the doorknob ;
-> While opening the Bottle Cap ;
-> While using a wrench to turn a lug nut

6. On the bases of application torques can either be
a Static or a Dynamic ;
-> A static torque is one which does not
produce an angular acceleration.
For instance; Someone pedalling a bicycle at
constant speed is told to a static torque as they
are not accelerating..
or
When some pushes an closed door as the door
is not rotating about its hinges , despite of force
applied.

7. -> A Dynamic torque is one which does produces
an angular acceleration.
For instance; The drive shaft in a racing car
accelerating from the start line is carrying a
dynamic torque because it must be producing
an angular acceleration of the wheels given that
the car is accelerating along the track.

8. Torque is a measure of how much a force is acting on an object
that cause that object to rotate,
it is defined as τ = r x F = r . F sinθ
where, τ = torque
F = linear force
r = distance measured from the axis of
rotation to where the linear force is applied.
θ = angle between F and r

9. The direction of the torque can be found by
using a conventional method that is RIGHT HAND
THUMB RULE .
That is if a hand is curled around the axis of
rotation with the fingers pointing in the direction
of the force , then the torque vector points is in
the direction of the thumb.

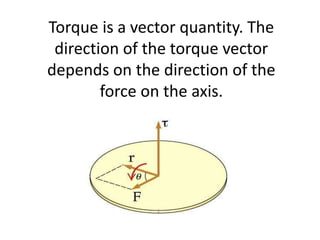
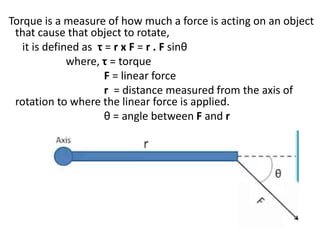
10. -> In the formula of the torque τ = r . F sinθ
In the equation , sinθ has no units , r has unit of
meters (m) and F has units of Newton(N) .
Combining these together the unit of torque is a
Newton-meter ( Nm).
-> The Dimensional formula for τ = [ M L2 T-2 ]
-> If the force vector θ = 0° or 180° the force will
not cause any rotation on the axis . The value of
torque for both this cases is zero.
-> The most effective force vectors to produce
torque are θ = 90° or -90°, which are
perpendicular to the position vector.

11. -> In Rotational Kinematics , torque takes the place
of the force in linear kinematics . There is direct
equivalent to Newton’s second law of motion (F=ma)
τ = Iα
Where , α = angular acceleration
I = rotational inertia, a property of a
rotating system Which depends on the mass
distribution of the system.
-> The larger the I , the harder is for an object to
acquire angular acceleration.

12. In the real-world , we often come across examples in
which more than one force is acting on a object .
The net torque is the sum of the individual torques.
In rotational equilibrium, there is no net torque on the
object . There may be individual torques, but they add
up to zero and cancels each other out.
For instance; In every car there is more than one
piston applying torque to the crankshaft. The total
torque is the sum of each individual torques
Total ( τ ) = τ(1) + τ(2) + ……..+ τ(n)
where n is the total number of torques being
applied to the object.

13. In case , of the rotational equilibrium this is when
the addition of all the torques is acting on a object
equals to zero, this means that there is no torque
acting on the object or all the torques acting on the
object are cancelling each other out.
For instance; a See-Saw..

15. -> The First image shows that the two children are
sitting on a see-saw that isn`t moving .
They are balanced at the axes of rotation .
-> In second image, both the children are exerting a
force down, with their weight , or known as the
force due gravity.
Child-1 is trying to rotate the see-saw counter
clockwise or anticlockwise and Child-2 is trying to
rotate it clockwise.
As long as the magnitudes of the two torques are
the same , they cancels each other out since they
are trying to move the see-saw in opposite direction.

16. THANK
YOU