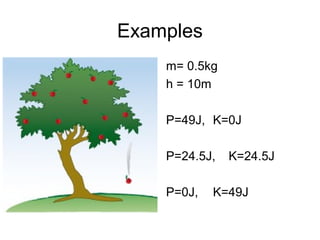
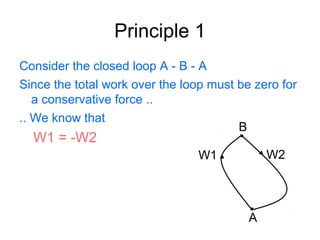
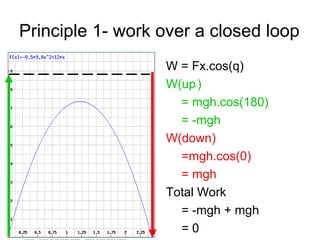
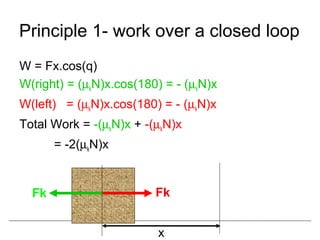
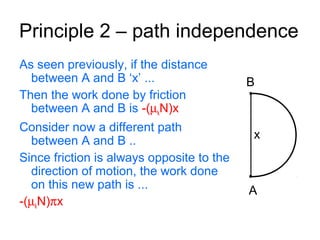
This document discusses conservative and non-conservative forces, and the principles of conservation of energy and mechanical energy. It states that for conservative forces, the total energy within a closed system remains the same, though it can transform between potential and kinetic forms. For conservative forces, the net work over a closed loop is zero, and the work is path independent. Friction is a non-conservative force where net work is done over a closed loop and more work is done over longer distances. Potential energy is the other form of energy involved in conservative systems, where the sum of potential and kinetic energy equals the total energy and changes in one form equal negative changes in the other.

1. Conservative and Non
Conservative Forces

2. Conservation of Energy
Energy in a closed system is always conserved
A closed system means that neither mass nor
energy can be transferred to or from outside this
system
It means that the total energy within the system
must remain the same.
However, energy can transform from one form to
another

3. Heat energy is
taken from the
drink to break the
bonds in the ice

4. Kinetic energy
of the stone is
transformed
into heat by the
friction

5. Conservation of mechanical energy
Consider a body in a CLOSED LOOP
A closed loop is a system where the body
returns again and again to the same
position
-eg: a mass on a spring
a bouncing ball
uniform circular motion

6. Conservative Forces
If the body is under the influence of a
CONSERVATIVE FORCE
.. The body will have the same KINETIC
ENERGY, (and velocity) at the beginning
and at the end of the loop.
Since WORK is the CHANGE in KINETIC
ENERGY, the net work in a closed loop
is..
.. Zero
No net work is done in a closed loop

7. Principle 1
Consider the closed loop A - B - A
Since the total work over the loop must be zero for
a conservative force ..
.. We know that
W1 = -W2
A
B
W1 W2

8. Now consider that W1 and W2 both have the same
starting and finish points.
Since in the previous situation, W1=-W2, then in
this situation, W1=W2
Principle 2
A
B
W1 W2
The work done is the
same irrespective of which
path is taken.
This is called:
PATH INDEPENDENCE

9. Conservative Forces
Gravity is the best example of a conservative force
Consider a ball that it is thrown directly upwards
and allowed to fall back to the ground

10. Principle 1- work over a closed loop
W = Fx.cos(q)
W(up)
= mgh.cos(180)
= -mgh
W(down)
=mgh.cos(0)
= mgh
Total Work
= -mgh + mgh
= 0

11. Principle 2 – path independence
Recall that it required the same amount of
work for gravity to bring the leaf down to
the ground, irrespective of its path.
q
h
h(cosq)

12. Non - conservative Forces
Friction is the best example of a non conservative
force
Consider a crate that is pushed a distance ‘x’ over
a ‘rough’ floor
And then pushed back to it’s original position

13. Principle 1- work over a closed loop
W = Fx.cos(q)
W(right) = (µkN)x.cos(180) = - (µkN)x
W(left) = (µkN)x.cos(180) = - (µkN)x
Total Work = -(µkN)x + -(µkN)x
= -2(µkN)x
Fk Fk
x

14. Principle 2 – path independence
B
A
x
As seen previously, if the distance
between A and B ‘x’ ...
Then the work done by friction
between A and B is -(µkN)x
Consider now a different path
between A and B ..
Since friction is always opposite to the
direction of motion, the work done
on this new path is ...
-(µkN)πx

15. Summary
CONSERVATIVE FORCES
Do no net work over a closed loop
(kinetic energy is conserved on returning to the
same position each time)
Do equal work between two points, irrespective of
its path
NON CONSERVATIVE FORCES
Do net work over a closed loop
(kinetic energy is lost on returning to the same
position each time)
Do more work over longer distances

16. Problem Sheet 4:

17. Solutions
1 A small disk of mass 4 kg moves in a circle of radius 1 m on a horizontal surface, with coefficient of kinetic
friction of .25. How much work is done by friction during the completion of one revolution?
• A disc moving with friction in a circle
• As we know with frictional force, the force exerted on the disc is constant throughout the journey, and has a
value of F k = μ k F n = (.25)(4kg)(9.8m/s 2) = 9.8N . At every point on the circle, this force points in the
opposite direction of the velocity of the disk. Also the total distance traveled by the disc is x = 2Πr = 2Π
meters. Thus the total work done is: W = Fx cosθ = (9.8N)(2Π)(cos180 o ) = - 61.6 Joules. Note that over this
closed loop the total work done by friction is nonzero, proving again that friction is a nonconservative force.
2 Consider the last problem, a small disk traveling in circle. In this case, however, there is no friction and the
centripetal force is provided by a string tied to the center of the circle, and the disk. Is the force provided by
the string conservative?
• To decide whether or not the force is conservative, we must prove one of our two principles to be true. We
know that, in the absence of other forces, the tension in the rope will remain constant, causing uniform
circular motion. Thus, in one complete revolution (a closed loop) the final velocity will be the same as the
initial velocity. Thus, by the Work-Energy Theorem, since there is no change in velocity, there is no net work
done over the closed loop. This statement proves that the tension is, in this case, indeed a conservative
force.
3 Calculus Based Problem Given that the force of a mass on a spring is given by F s = - kx , calculate the net
work done by the spring over one complete oscillation: from an initial displacement of d, to -d, then back to
its original displacement of d. In this way confirm the fact that the spring force is conservative.
• a) initial position of mass. b) position of mass halfway through oscillation. c) final position of mass
• To calculate the total work done during the trip, we must evaluate the integral W = F(x)dx . To since the
mass changes directions, we must actually evaluate two integrals: one from d to –d, and one from –d to d:
• W = -kxdx + -kxdx = [- kx 2]d -d + [- kx 2]-d d = 0 + 0 = 0
• Thus the total work done over a complete oscillation (a closed loop) is zero, confirming that the spring force
is indeed conservative.

18. Potential Energy
If
And
Then
Mechanical energy is conserved under
conservative forces
Kinetic energy varies under work
There must be at least another form of
energy involved in the system
This energy is called POTENTIAL ENERGY
It is usually represented by the letter ‘U’
This energy increases as kinetic energy decreases,
and vice versa

19. This implies…
U + K = E
Potential Energy + Kinetic Energy = Total Energy
dU = -dK
The change in Potential Energy is equal to the
negative change in Kinetic Energy
Ui + Ki = Uf + Kf = E
The sum of Potential and Kinetic Energies is
constant

20. Also …
Since
And
Then
Since
Then
W = δK
W = F(x).dx
δK = F(x).dx
δU = -δK
δU = - F(x).dx
= - W

21. m= 0.5kg
h = 10m
P=49J, K=0J
P=24.5J, K=24.5J
P=0J, K=49J
Examples