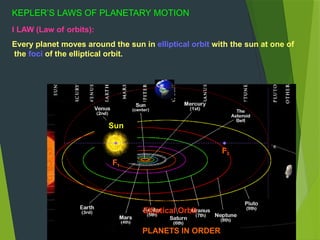
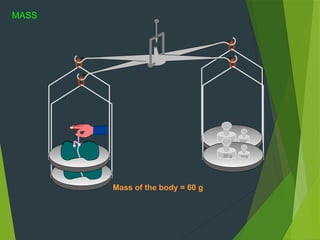
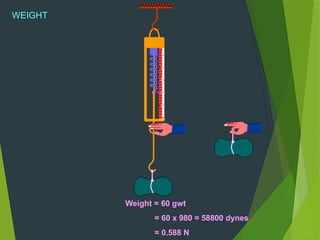
Sir Isaac Newton and Johannes Kepler contributed to our understanding of gravitation, explaining how the Earth attracts objects with a gravitational force that governs motion. Newton's universal law of gravitation establishes that every body attracts every other body with a force proportional to their masses and inversely proportional to the square of the distance between them. Gravitational force has unique properties, including being the weakest force in nature, acting as an attractive force, and influencing the orbits of celestial bodies, demonstrating foundational principles that govern the universe.

1. GRAVITATION
Sir Issac Newton
(1643 -1727)
Johannes Kepler
(1571-1630)

2. Gravitational force of the earth or Gravity
A force is necessary to produce motion in a body.
A body dropped from a height falls towards the earth. It indicates that the
earth exerts a force of attraction (called gravity) on the body.
In fact, the earth attracts all the objects towards its centre.
The force with which the earth pulls the objects towards it is called the
gravitational force of the earth or gravity.
The gravitational force between the sun and the earth keeps the earth in
uniform circular motion around the sun.
The gravitational force of the earth (or gravity) is responsible –
for holding the atmosphere above the earth
for the rain falling to the earth
for flow of water in the rivers
for keeping us firmly on the earth,
for the revolution of moon around the
earth, etc.

3. NEWTON’S UNIVERSAL LAW OF GRAVITATION
Every body in the universe attracts every other body with a force which is
directly proportional to the product of their masses and is inversely
proportional to the square of the distance between them.
The direction of force is along the line joining the centres of the two
bodies.
r
m1
m2
i.e. F α
1
r2
Let two bodies A and B of masses m1 and m2 are placed at a distance of ‘r’
from each other. Let ‘F’ be the force of attraction between the bodies.
Then,
(i) the force of attraction is directly proportional the product of their
masses
i.e. F α m1 x m2
(ii) the force of attraction is inversely proportional the square of the distance
between them

4. or
F α
m1 x m2
r2
where G is a constant called as
“universal gravitational constant”
m1 x m2
F = G
r2
Properties of gravitational force
1. Gravitational force is the weakest force in nature.
2. It is an attractive force. (Unlike electrostatic and magnetic force;
they
are both attractive and repulsive)
3. It is a mutual force. (First body attracts the second body and the
second body attracts the first body with equal force)
4. It is a central force. (Acts along the line joining the centres of the
bodies)
5. It is mass and distance dependent.
6. It obeys inverse square law.
7. It is a long range force. (It decreases with distance as per inverse square
law and becomes zero only at infinite distance – like electrostatic and
magnetic force)
8. It does not depend on the medium between the interacting bodies.

5. • The value of Universal Gravitational Constant G is 6.67 x 10-11
N m2
Kg-2
.
• The value of G does not depend on the medium between two bodies.
• The value of G is same throughout the Universe and hence the name.
•Universal Gravitational Constant G is different from acceleration due to
gravity g. Therefore correct symbol must be used accordingly.
• SI unit of G is N m2
Kg-2
.
• If two bodies of mass 1 kg each are separated by 1 m from each other,
then, G = F.
* Therefore, Universal gravitational constant G is numerically equal to the
force of gravitation which exists between two bodies of unit masses kept at
a unit distance from each other.
G = F
r2
m1 x m2
Universal Gravitational Constant (G)

6. Gravitational force is the weakest force of all.
If two bodies of mass 1 kg each are separated by 1 m from each other,
then, F = G = 6.67 x 10-11
N
Though the various objects on this earth attract one another constantly, they
do not cause any visible motion because the gravitational force of attraction
between them is very, very small.
Imagine a situation on the earth if the objects continuously move towards
each other due to gravitational force between them !
When both the objects are very big, having very large masses, then the
gravitational force of attraction between them becomes extremely large.
The gravitational force due to earth on an object of mass 1 kg placed on the
ground is 9.8 N.
The gravitational force between the earth and the moon even at a large
distance is very large and is 2 x 1020
N.

7. KEPLER’S LAWS OF PLANETARY MOTION
I LAW (Law of orbits):
Every planet moves around the sun in elliptical orbit with the sun at one of
the foci of the elliptical orbit.
F1
F2
Sun
Elliptical Orbit
PLANETS IN ORDER

8. F1
F2
Sun
S
II LAW (Law of areas):
The line joining the planet to the sun sweeps over equal areas in equal
intervals of time.
C
Elliptical Orbit
B
Apogee
A
Perigee
D
Area of SAB = Area of SCD (For the
given time)
II law tells us that a planet does not move with constant speed around the
sun. It speeds up while approaching the nearest point called ‘perigee’ and
slows down while approaching the farthest point called ‘apogee’.
Therefore, distance covered on the orbit with in the given interval of time at
perigee is greater than that at apogee such that areas swept are equal.

9. Though Kepler gave the laws of planetary motion, he could not give a theory
to explain the motion of planets.
Only Newton explained that the cause of the motion of the planets is the
gravitational force which the sun exerts on them.
Newton used Kepler’s III law to develop the law of universal gravitation.
= constant
r3
III LAW (Law of periods):
The square of the time period of revolution of a planet around the sun is
directly proportional to the cube of the mean distance of a planet from the
sun.
The law is mathematically expressed as
T2
α r3
T2
or

10. FREE FALL
When a body falls from a height towards the
earth only under the influence of the
gravitational force (with no other forces acting
on it), the body is said to have a free fall.
The body having a free fall is called a ‘freely
falling body’.
Galileo proved that the acceleration of an object
falling freely towards the earth does not
depend on the mass of the object.
Imagine that vacuum is created by evacuating
the air from the glass jar.
The feather and the coin fall with same
acceleration and reach the ground at the same
time.

11. Acceleration due to gravity (g)
Acceleration due to gravity is defined as the uniform acceleration produced
in a freely falling body due to the gravitational force of the earth.
Acceleration due to gravity (g) = 9.8 m/s2
= 980 cm/s2
.
Calculation of acceleration due to gravity (g)
Suppose a body of mass ‘m’ is placed on the earth of mass ‘M’ and radius
‘R’.
According to Newton’s universal law of gravitation,
Force exerted by the earth on the body is given by
R
m
M
F = G
M x m
R2
This force exerted by the earth produces an acceleration on the body.
Therefore, F = mg (g - acceleration due to gravity)
From the two equations, we have
mg = G
M x m
R2
or
G M
g =
R2

12. Acceleration due to gravity on the earth is calculated as follows:
Mass of the earth
Radius of the earth
= 6 x 1024
kg
= 6.4 x 106
m
g =
Gravitational constant = 6.67 x 10-11
N m2
kg-2
G M
R2
Substituting the values, we get 9 = 9.8 m/s2
For simplified calculations we can take g as 10 m/s2
Variation of acceleration due to gravity (g)
1. Acceleration due to gravity decrease with altitude.
h
M
m
R
g =
R2
g’ =
G M G M
(R+h)2

16. The Variation of g with respect to Depth and Height
(graph).
The Variation of g with respect to height will never be
zero. It will increase after certain height.
The Variation of g with respect to depth will be zero
when the body is placed at the center of earth.

18. EQUATIONS OF VERTICAL MOTION (Under the influence of g)
Let a body be thrown vertically downward with initial velocity ‘u’. Let the
final velocity of the body after time ‘t’ be ‘v’. Let ‘h’ be the height (vertical
distance) covered by the body and ‘g’ be the acceleration due to gravity.
Then the equations of motion are:
v = u + gt
h = ut + ½ gt2
v2 = u2
+ 2gh
When a body is dropped freely, the equations of motion are:
v = gt
h = ½ gt2
v2 = 2gh
When a body is thrown vertically upwards, the equations of motion are:
v = u - gt
h = ut - ½ gt2
2 = u2
- 2gh
-u, -v -g, -h
u = 0, -v -g, -h
+u, +v -g, +h

19. Cartesian Sign Conventions for Vertical Motion
1. The physical quantities having vertically upward motion are assigned
positive values.
2. On the other hand, the physical quantities having vertically downward
motion are assigned negative values.
3. Acceleration due to gravity (g) always acts in the downward direction and
hence taken negative.
TIPS TO SOLVE THE NUMERICAL PROBLEMS
4. g is always taken negative.
5. When a body is dropped freely its initial velocity u = 0.
6. When a body is thrown vertically upwards, its final velocity becomes zero
at the maximum height.
7. The time taken by a body to rise to the highest point is equal to the time it
takes to fall from the same height.

20. 50 g 10 g
50 g 10 g
Mass of the body = 60 g
MASS

21. The mass of a body is the quantity of matter contained in it.
Mass of a body is a measure of inertia of the body and hence called
inertial mass.
Mass is a scalar quantity.
SI unit of mass is kilogramme or kg.
CGS unit of mass is gramme or g.
Mass of a body is constant and does not change from place to place.
Mass is measured by a beam or common balance.
Mass of a body can not be zero.

22. Weight = 60 gwt
= 60 x 980 = 58800 dynes
= 0.588 N
0
20
40
60
80
100
WEIGHT

23. The weight of a body on the earth is the force with which it is attracted
towards the centre of the earth.
Weight = mass x acceleration due to gravity
W = m x g
SI unit of weight is ‘newton’ or N
Weight of 1 kg mass is 9.8 newton.
Weight is a vector quantity since it has both magnitude and direction.
Weight changes from place to place.
Weight is measured by a spring balance.
Weight of a body can be zero. When a body is taken to the centre
of the earth, acceleration due to gravity at the centre is zero and
hence weight is zero.
On the moon, acceleration due to gravity is nearly 1/6th of that on the
earth and hence the weight of a body on the moon is 1/6th of its weight
on the earth.

24. GARVITATIONAL FIELD
The space around a material body in which its gravitational pull can be experienced is
called its gravitational field.
INTENSITY OF GRAVITATIONAL FIELD
The intensity of the gravitational field is defined as the force experienced by a body of
unit mass placed at that point provided the presence of unit mass does not disturb the
original gravitational field.
It is always towards the centre of gravity of the body whose gravitational field is
considered.
Let M be the mass of a body with centre of gravity at O. Let F be the gravitational force
of attraction experienced by a test mass mo when placed at P in the gravitational field,
where OP=x .
According to Newton’s law of gravitation F= GM mo/x2
Intensity of gravitational field at P will be
I= F/mo
= GMmo/x2
mo
= GM
x2

25. GRAVITATIONAL POTENTIAL
Gravitational potential at a point in a gravitational field of a body is defined as the
amount of work done in bringing a body of unit mass from infinity to that point without
acceleration.
If W is the amount of work done in bringing a body of mass mo from infinity to a point P in
the gravitational field without acceleration, then gravitational potential at P= W/mo.
Gravitational potential is a scalar quantity. It is represented by Vp.
Vp= -GM/r
The gravitational potential at a point is always negative.
GRAVITATIONAL POTENTIAL ENERGY
The potential energy of a body at a given position is defined as the energy stored in the
body while bringing it form the position of zero potential energy to that position.
Gravitational potential energy of a body at a point in a gravitational field of another body is
defined as the amount of work done in bringing the given body from infinity to that point
without acceleration.
U = -GMm/r
U = Vp m
Gravitational potential energy = gravitational potential mass of the body

26. CENTRE OF GRAVITY
Centre of gravity of a body placed in the gravitational field is that point where
the net gravitational field is that point where the net gravitational force of the
field acts.
SATELLITE
A satellite is a body which is revolving continuously in an orbit around a
comparatively much larger body. In our solar planet each planet is a satellite of
sun. Moon is natural satellite of our planet earth.

27. ORBITAL SPEED, TIME PERIOD & HEIGHT OF
SATELLITE
(1) Orbital speed: Orbital speed of a satellite is the minimum speed required to
put the satellite into a given orbit around earth.
The value of orbital speed is different for different orbits around earth & is
independent of the mass of satellite. Let
M= mass of earth, R= radius of earth
m= mass of the satellite , v= orbital speed of satellite
h= height of satellite above the surface of earth
r= radius of orbit of satellite= R+h
The centripetal force required to the satellite in its orbit,
F=mv2
/r

28. According to Newton’s law of gravitation, gravitational pull acting on satellite
= GMm/r2
In equilibrium, the gravitational pull provides the required centripetal force to satellite.
mv2
/r= GMm /r2
or v=
v = = R
When a satellite is orbiting very close to the surface of earth h<<R, then
r=R+hR & v=vo(say)
vo=R =
Substituting ,
g=9.8 m/s2
& R= 6.4 10
6
m
vo= = 7.92 km s-1

29. (2) Time period of satellite: It is the time taken by satellite to complete one
revolution around the earth & is denoted by T.
T= distance travelled in 1 revolution = 2
orbital velocity v
T= 2 = 2 …(1)
R R
If the earth is supposed to be a sphere of mean density
Then mass of earth is M= 4R3
/3 g=GM/R2
=4GR/3
Substituting this value of g in (1), we get
T= ...(2)
For a satellite orbiting close to the surface of earth, h<<R h+RR
From (2), T= From (1), T= 2 …(3)
By substituting g=9.8 m/s2
& R= 6.4 10
6
m in (3), we get
T=84.6 minutes

30. ENERGY OF AN ORBITIN G SATELLITE
The total mechanical energy (E) of a satellite revolving around the earth is the sum
of its potential energy(U) & kinetic energy(K)
U= -GMm/r
K= mv2
/2= GMm/2r [v2
=GM/r]
E= U+K= -GMm/2r
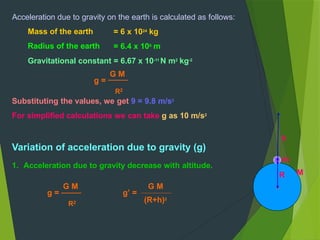
E= -GMm = -GMm
2r 2(R+h)
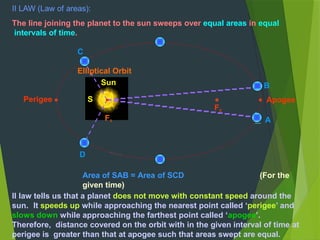
Since, a satellite is always at finite distance from earth, its total energy is negative
& can never be positive or zero.
BINDING ENERGY OF A SATELLITE
The energy required to remove the satellite from its orbit around the earth to infinity
is called Binding energy of the satellite. Binding energy is equal to negative value of
total mechanical energy of a satellite in its orbit.
Thus, binding energy = -E = GMm = GMm
2r 2(R+h)

31. GEOSTATIONARY OR GEOSYNCHRONOUS SATELLITES
A satellite which appears to be at fixed position at a definite height to an
observer on earth is called geostationary satellite. This satellite is also called as
geosynchronous satellite as its angular speed is synchronized with the angular
speed of the earth about its axis, i.e., this satellite revolves around the earth
with the same angular speed in the same direction as is done by earth around its
axis.
Height of geostationary satellite
h= T
2
R
2
g
2 1/3
– R
4
Geostationary satellites are used for the purposes of communication as they act
as reflectors of suitable waves carrying messages. Therefore, they are also called
communication satellites. Telstar was the first communication satellite
launched by U.S.A. in 1962.
INSAT 2B & INSAT 2C are the communication satellites of India.

32. IMPORTANT USES OF SATELLITES
1. In communicating radio, T.V. & telephone signals across the oceans.
2. In forecasting weather.
3. In studying the upper region of atmosphere.
4. To determine the exact shape & dimensions of earth.
5. In the study of cosmic rays & solar radiations.
INDIA LEAD INTO SPACE
 In 1975, India launched its first low orbit satellite Arya bhatt.
 The first Indian experimental satellite, i.e., Apple was launched on
June 19 , 1981
 In 1984, Rakesh Sharma become the first Indian to go into space.

33. ESCAPE SPEED
Escape speed on earth is defined as the minimum speed with which a body has
to be projected vertically upwards from the surface of earth so that it just
crosses the gravitational field of earth & never returns on its own.
It is denoted by ve.
ve= = For earth, ve= 11.2 km s-1
WEIGHTLESSNESS
It is a situation in which the observed weight of the body becomes zero.
Problems of weightlessness
 If an astronaut is walking in space craft, he may be pushed away from the
floor & may crash against the ceiling of the space craft.
 The space-flight for a long time, adversely affects the human organism.
 The experiment of simple pendulum can not be performed in the
weightlessness state because
T=2 = as g=0