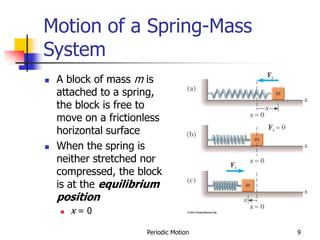
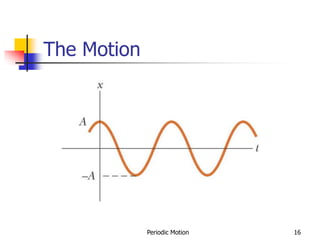
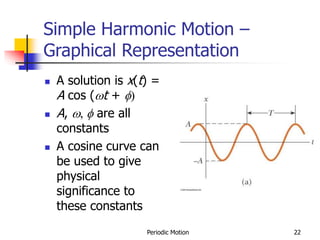
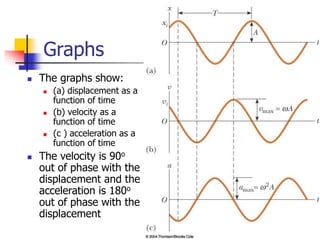
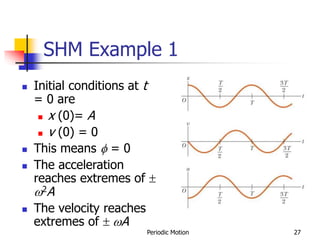
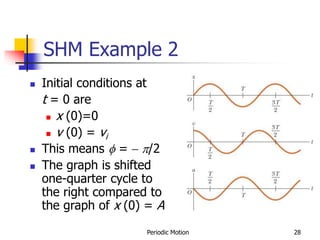
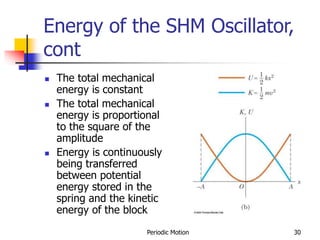
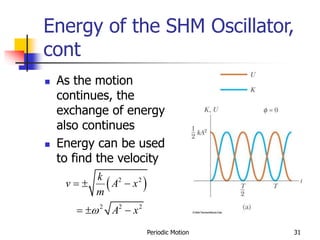
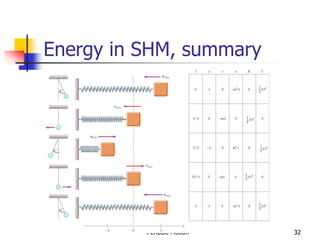
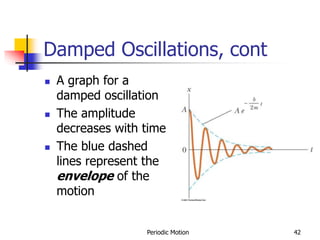
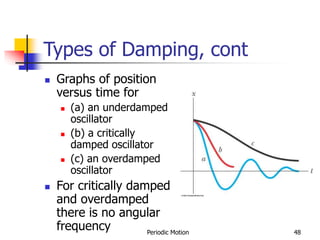
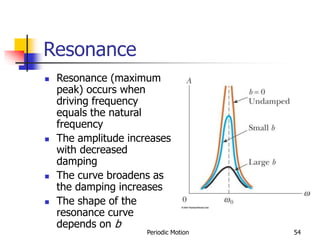
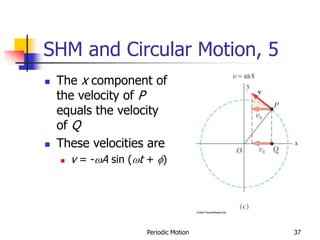
1) The document discusses periodic motion and simple harmonic motion. It provides equations and graphs describing the displacement, velocity, and acceleration of objects undergoing SHM. 2) Damped oscillations are discussed where a damping force like friction causes the amplitude of the oscillations to decrease over time as the mechanical energy is dissipated. 3) The relationship between SHM and circular motion is explained where the x-component of uniform circular motion traces out a simple harmonic pattern.

1. Periodic Motion 1
Chapter 15
Oscillatory Motion
April 17th, 2006

2. Periodic Motion 2
The last steps …
 If you need to, file your taxes TODAY!
– Due at midnight.
 This week
– Monday & Wednesday – Oscillations
– Friday – Review problems from earlier in the
semester
 Next Week
– Monday – Complete review.

3. Periodic Motion 3
The FINAL EXAM
 Will contain 8-10 problems. One will
probably be a collection of multiple choice
questions.
 Problems will be similar to WebAssign
problems but only some of the actual
WebAssign problems will be on the exam.
 You have 3 hours for the examination.
 SCHEDULE: MONDAY, MAY 1 @ 10:00 AM

4. Periodic Motion 4
Things that Bounce
Around

5. Periodic Motion 5
The Simple Pendulum
0
1
)
sin(
2
2
2
2
2













L
g
dt
d
dt
d
mL
L
mg
I

6. Periodic Motion 6
The Spring
0
2
2
2
2











x
m
k
dt
x
d
dt
x
d
m
kx
ma
F

7. Periodic Motion 7
Periodic Motion
 From our observations, the motion of these
objects regularly repeats
 The objects seem t0 return to a given position
after a fixed time interval
 A special kind of periodic motion occurs in
mechanical systems when the force acting on
the object is proportional to the position of
the object relative to some equilibrium
position
 If the force is always directed toward the
equilibrium position, the motion is called simple
harmonic motion

8. Periodic Motion 8
The Spring … for a moment
 Let’s consider its motion at each point.
 What is it doing?
 Position
 Velocity
 Acceleration

9. Periodic Motion 9
Motion of a Spring-Mass
System
 A block of mass m is
attached to a spring,
the block is free to
move on a frictionless
horizontal surface
 When the spring is
neither stretched nor
compressed, the block
is at the equilibrium
position
 x = 0

10. Periodic Motion 10
More About Restoring Force
 The block is
displaced to the
right of x = 0
 The position is
positive
 The restoring force
is directed to the left

11. Periodic Motion 11
More About Restoring Force, 2
 The block is at the
equilibrium position
 x = 0
 The spring is neither
stretched nor
compressed
 The force is 0

12. Periodic Motion 12
More About Restoring Force, 3
 The block is
displaced to the left
of x = 0
 The position is
negative
 The restoring force
is directed to the
right

13. Periodic Motion 13
Acceleration, cont.
 The acceleration is proportional to the
displacement of the block
 The direction of the acceleration is opposite
the direction of the displacement from
equilibrium
 An object moves with simple harmonic
motion whenever its acceleration is
proportional to its position and is oppositely
directed to the displacement from equilibrium

14. Periodic Motion 14
Acceleration, final
 The acceleration is not constant
 Therefore, the kinematic equations cannot
be applied
 If the block is released from some position
x = A, then the initial acceleration is –kA/m
 When the block passes through the
equilibrium position, a = 0
 The block continues to x = -A where its
acceleration is +kA/m

15. Periodic Motion 15
Motion of the Block
 The block continues to oscillate
between –A and +A
 These are turning points of the motion
 The force is conservative
 In the absence of friction, the motion
will continue forever
 Real systems are generally subject to
friction, so they do not actually oscillate
forever

16. Periodic Motion 16
The Motion

17. Periodic Motion 17
Vertical Spring
Equilibrium Point

18. Periodic Motion 18
Ye Olde Math
0
2
2







 x
m
k
dt
x
d
0
2
2

 

L
g
dt
d
0
2
2
2

 q
dt
q
d


19. Periodic Motion 19
0
2
2
2

 q
dt
q
d

)
cos(
:
0 t
q
q
Solution


 q is either the displacement of the spring (x)
or the angle from equilibrium ().
 q is MAXIMUM at t=0
 q is PERIODIC, always returning to its
starting position after some time T called the
PERIOD.

20. Periodic Motion 20
Example – the Spring
m
k
f
k
m
T
t
m
k
T
t
m
k
m
k
t
m
k
x
x
x
m
k
dt
x
d




2
1
2
2
)
(
)
(
so
same,
the
stays
function
T,
t
When t
sin
0
2
0
2
2












21. Periodic Motion 21
Example – the Spring
L
g
f
g
L
T
t
L
g
T
t
L
g
L
g
t
L
g
L
g
dt
d








2
1
2
2
)
(
)
(
so
same,
the
stays
function
T,
t
When t
sin
0
2
0
2
2












22. Periodic Motion 22
Simple Harmonic Motion –
Graphical Representation
 A solution is x(t) =
A cos (t + f)
 A, , f are all
constants
 A cosine curve can
be used to give
physical
significance to
these constants

23. Periodic Motion 23
Simple Harmonic Motion –
Definitions
 A is the amplitude of the motion
 This is the maximum position of the
particle in either the positive or negative
direction
  is called the angular frequency
 Units are rad/s
 f is the phase constant or the initial
phase angle

24. Periodic Motion 24
Motion Equations for Simple
Harmonic Motion
 Remember, simple harmonic motion is
not uniformly accelerated motion
2
2
2
( ) cos ( )
sin( t )
cos( t )
x t A t
dx
v A
dt
d x
a A
dt
 f
  f
  f
 
   
   

25. Periodic Motion 25
Maximum Values of v and a
 Because the sine and cosine functions
oscillate between 1, we can easily find
the maximum values of velocity and
acceleration for an object in SHM
max
2
max
k
v A A
m
k
a A A
m


 
 

26. Periodic Motion 26
Graphs
 The graphs show:
 (a) displacement as a
function of time
 (b) velocity as a
function of time
 (c ) acceleration as a
function of time
 The velocity is 90o
out of phase with the
displacement and the
acceleration is 180o
out of phase with the
displacement

27. Periodic Motion 27
SHM Example 1
 Initial conditions at t
= 0 are
 x (0)= A
 v (0) = 0
 This means f = 0
 The acceleration
reaches extremes of 
2A
 The velocity reaches
extremes of  A

28. Periodic Motion 28
SHM Example 2
 Initial conditions at
t = 0 are
 x (0)=0
 v (0) = vi
 This means f =  /2
 The graph is shifted
one-quarter cycle to
the right compared to
the graph of x (0) = A

29. Periodic Motion 29
Energy of the SHM Oscillator
 Assume a spring-mass system is moving on a
frictionless surface
 This tells us the total energy is constant
 The kinetic energy can be found by
 K = ½ mv 2 = ½ m2 A2 sin2 (t + f)
 The elastic potential energy can be found by
 U = ½ kx 2 = ½ kA2 cos2 (t + f)
 The total energy is K + U = ½ kA 2

30. Periodic Motion 30
Energy of the SHM Oscillator,
cont
 The total mechanical
energy is constant
 The total mechanical
energy is proportional
to the square of the
amplitude
 Energy is continuously
being transferred
between potential
energy stored in the
spring and the kinetic
energy of the block

31. Periodic Motion 31
 As the motion
continues, the
exchange of energy
also continues
 Energy can be used
to find the velocity
Energy of the SHM Oscillator,
cont
 )
2 2
2 2 2
k
v A x
m
A x

  
  

32. Periodic Motion 32
Energy in SHM, summary

33. Periodic Motion 33
SHM and Circular Motion
 This is an overhead
view of a device that
shows the relationship
between SHM and
circular motion
 As the ball rotates with
constant angular
velocity, its shadow
moves back and forth in
simple harmonic motion

34. Periodic Motion 34
SHM and Circular Motion, 2
 The circle is called a
reference circle
 Line OP makes an
angle f with the x
axis at t = 0
 Take P at t = 0 as
the reference
position

35. Periodic Motion 35
SHM and Circular Motion, 3
 The particle moves
along the circle with
constant angular
velocity 
 OP makes an angle
 with the x axis
 At some time, the
angle between OP
and the x axis will
be   t + f

36. Periodic Motion 36
SHM and Circular Motion, 4
 The points P and Q always have the
same x coordinate
 x (t) = A cos (t + f)
 This shows that point Q moves with
simple harmonic motion along the x
axis
 Point Q moves between the limits A

37. Periodic Motion 37
SHM and Circular Motion, 5
 The x component of
the velocity of P
equals the velocity
of Q
 These velocities are
 v = -A sin (t + f)

38. Periodic Motion 38
SHM and Circular Motion, 6
 The acceleration of
point P on the reference
circle is directed radially
inward
 P ’s acceleration is a =
2A
 The x component is
–2 A cos (t + f)
 This is also the
acceleration of point Q
along the x axis

39. Periodic Motion 39
SHM and Circular Motion,
Summary
 Simple Harmonic Motion along a straight line
can be represented by the projection of
uniform circular motion along the diameter of
a reference circle
 Uniform circular motion can be considered a
combination of two simple harmonic motions
 One along the x-axis
 The other along the y-axis
 The two differ in phase by 90o

40. Periodic Motion 40
Simple Pendulum, Summary
 The period and frequency of a simple
pendulum depend only on the length of
the string and the acceleration due to
gravity
 The period is independent of the mass
 All simple pendula that are of equal
length and are at the same location
oscillate with the same period

41. Periodic Motion 41
Damped Oscillations
 In many real systems, nonconservative
forces are present
 This is no longer an ideal system (the type
we have dealt with so far)
 Friction is a common nonconservative force
 In this case, the mechanical energy of
the system diminishes in time, the
motion is said to be damped

42. Periodic Motion 42
Damped Oscillations, cont
 A graph for a
damped oscillation
 The amplitude
decreases with time
 The blue dashed
lines represent the
envelope of the
motion

43. Periodic Motion 43
Damped Oscillation, Example
 One example of damped
motion occurs when an
object is attached to a
spring and submerged in a
viscous liquid
 The retarding force can be
expressed as R = - b v
where b is a constant
 b is called the damping
coefficient

44. Periodic Motion 44
Damping Oscillation, Example
Part 2
 The restoring force is – kx
 From Newton’s Second Law
SFx = -k x – bvx = max
 When the retarding force is small
compared to the maximum restoring
force we can determine the expression
for x
 This occurs when b is small

45. Periodic Motion 45
Damping Oscillation, Example,
Part 3
 The position can be described by
 The angular frequency will be
2
cos( )
b
t
m
x Ae t
 f

 
2
2
k b
m m

 
   
 

46. Periodic Motion 46
Damping Oscillation, Example
Summary
 When the retarding force is small, the
oscillatory character of the motion is
preserved, but the amplitude decreases
exponentially with time
 The motion ultimately ceases
 Another form for the angular frequency
where 0 is the angular
frequency in the
absence of the retarding
force
2
2
0
2
b
m
 
 
   
 

47. Periodic Motion 47
Types of Damping
 is also called the natural
frequency of the system
 If Rmax = bvmax < kA, the system is said to be
underdamped
 When b reaches a critical value bc such that
bc / 2 m = 0 , the system will not oscillate
 The system is said to be critically damped
 If Rmax = bvmax > kA and b/2m > 0, the
system is said to be overdamped
0
k
m
 

48. Periodic Motion 48
Types of Damping, cont
 Graphs of position
versus time for
 (a) an underdamped
oscillator
 (b) a critically
damped oscillator
 (c) an overdamped
oscillator
 For critically damped
and overdamped
there is no angular
frequency

49. Periodic Motion 49
Forced Oscillations
 It is possible to compensate for the loss
of energy in a damped system by
applying an external force
 The amplitude of the motion remains
constant if the energy input per cycle
exactly equals the decrease in
mechanical energy in each cycle that
results from resistive forces

50. Periodic Motion 50
Forced Oscillations, 2
 After a driving force on an initially
stationary object begins to act, the
amplitude of the oscillation will increase
 After a sufficiently long period of time,
Edriving = Elost to internal
 Then a steady-state condition is reached
 The oscillations will proceed with constant
amplitude

51. Periodic Motion 51
Forced Oscillations, 3
 The amplitude of a driven oscillation is
 0 is the natural frequency of the
undamped oscillator
 )
0
2
2
2 2
0
F
m
A
b
m

 

 
   
 

52. Periodic Motion 52
Resonance
 When the frequency of the driving force
is near the natural frequency (  0)
an increase in amplitude occurs
 This dramatic increase in the amplitude
is called resonance
 The natural frequency 0 is also called
the resonance frequency of the system

53. Periodic Motion 53
Resonance
 At resonance, the applied force is in
phase with the velocity and the power
transferred to the oscillator is a
maximum
 The applied force and v are both
proportional to sin (t + f)
 The power delivered is F . v
 This is a maximum when F and v are in phase

54. Periodic Motion 54
Resonance
 Resonance (maximum
peak) occurs when
driving frequency
equals the natural
frequency
 The amplitude increases
with decreased
damping
 The curve broadens as
the damping increases
 The shape of the
resonance curve
depends on b

55. Periodic Motion 55
WE ARE DONE!!!