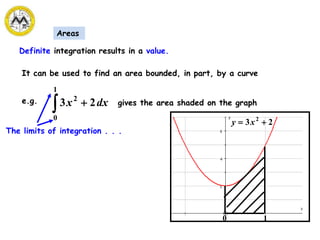
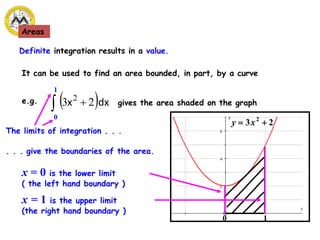
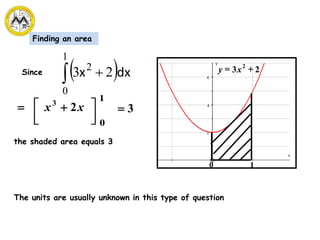
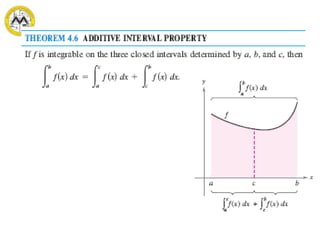
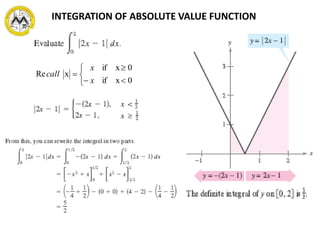
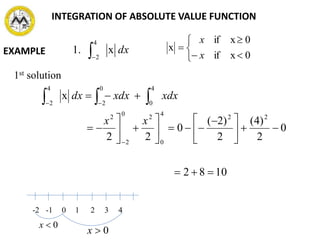
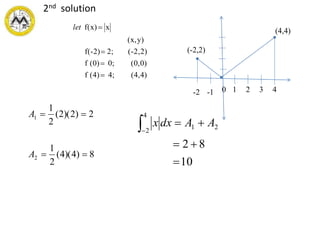
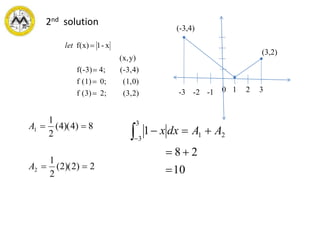
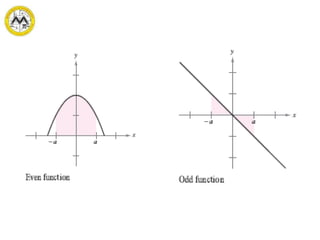
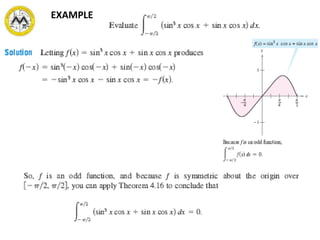
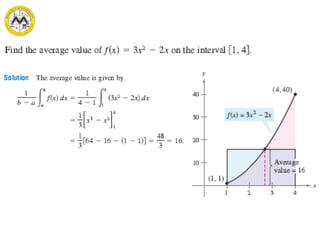
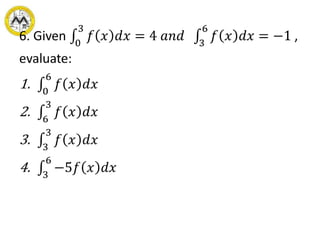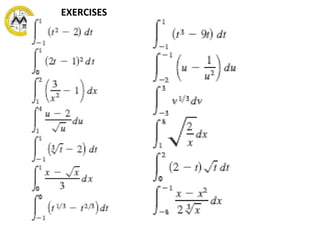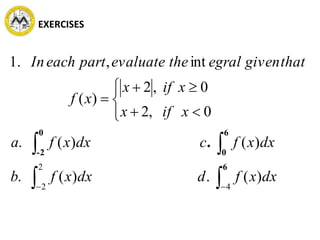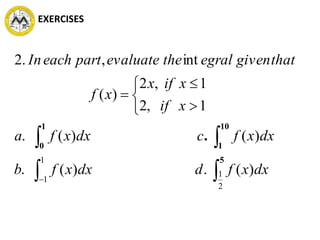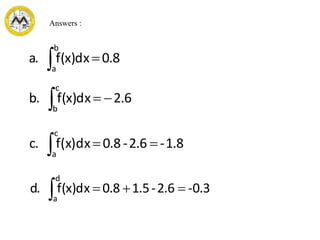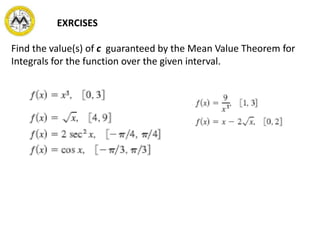The document defines definite integrals and discusses their properties. It states that a definite integral evaluates to a single number by integrating a function over a closed interval from a lower limit to an upper limit. It gives examples of using definite integrals to find areas bounded by curves. The mean value theorem for integrals is also introduced, which states that there is a rectangle between the inscribed and circumscribed rectangles with an area equal to the region under the curve. Exercises are provided on evaluating definite integrals and applying the mean value theorem.

1. DEFINITE INTEGRALS

2. OBJECTIVES
At the end of the lesson, the students are expected to:
• define and interpret definite integral.
• identify and distinguish the different properties of the definite
integrals.
• evaluate definite integrals.
• understand and use the mean Value Theorem for Integrals.
• find the average value of a function over a closed interval.

3. If F(x) is the integral of f(x)dx, that is, F’(x) = f(x)dx and if a and b are
constants, then the definite integral is:
 
)a(F)b(F
xFdx)x(f
b
a
b
a


where a and b are called lower and upper limits of
integration, respectively.
The definite integral link the concept of area to other important
concepts such as length, volume, density, probability, and other
work.
THE DEFINITE INTEGRAL

4. 0 1
23 2
 xy
It can be used to find an area bounded, in part, by a curve
e.g.
 
1
0
2
23 dxx gives the area shaded on the graph
The limits of integration . . .
Definite integration results in a value.
Areas

5. . . . give the boundaries of the area.
The limits of integration . . .
0 1
23 2
 xy
It can be used to find an area bounded, in part, by a curve
Definite integration results in a value.
Areas
x = 0 is the lower limit
( the left hand boundary )
x = 1 is the upper limit
(the right hand boundary )
   dxx 23 2
0
1
e.g. gives the area shaded on the graph

6. 0 1
23 2
 xy
Finding an area
the shaded area equals 3
The units are usually unknown in this type of question
  
1
0
2
23 dxxSince
3
1
0



 xx 23


7. xxy 22
xxy 22

Finding an area
 


0
1
2
2 dxxxAarea
A B
  
1
0
2
2 dxxxBarea
For parts of the curve below the x-
axis, the definite integral is negative,
so

12. EXAMPLE

14. EXERCISES

15. INTEGRATION OF ABSOLUTE VALUE FUNCTION
0xif
0xif
xRe






x
x
call

16. INTEGRATION OF ABSOLUTE VALUE FUNCTION
EXAMPLE dxx.1
4
2
1082
0
2
)4(
2
)2(
0
22
x
224
0
20
2
2
4
0
0
2
4
2






 









 
xx
xdxxdxdx
1st solution
0xif
0xif
x






x
x
0 1-2 32 4-1
0x
0x

17. 2nd solution
(4,4)4;(4)f
(0,0)0;(0)f
,2)(-22;f(-2)
y)(x,
xf(x)



let
-1 1-2 432
(4,4)
(-2,2)
0
8)4)(4(
2
1
2)2)(2(
2
1
2
1


A
A
10
82
21
4
2



AAdxx

18. 

3
3
1.2 dxx
1st solution
 





1x0,x-1if1
1x0,x-1if1
1
x
x
x
   
10
2
20
2
1
2
3
2
15
2
1
22
x
-x
111
3
1
21
3
2
3
1
1
3
3
3










 
x
x
dxxdxxdxx

19. 2nd solution
(3,2)2;(3)f
(1,0)0;(1)f
,4)(-34;f(-3)
y)(x,
x-1f(x)



let
-1 1-2-3 32
(3,2)
(-3,4)
0
2)2)(2(
2
1
8)4)(4(
2
1
2
1


A
A
10
28
1 21
3
3



AAdxx

20. EXERCISES

21. INTEGRATION OF ODD AND EVEN FUNCTIONS
 
 x-integers,oddFor
;x-integers,evenFor
:Re
nn
nn
x
x
call


fofdomainxallforf(x)f(-x)ifevenbetosaidis Function
fofdomainxallforf(x)f(-x)ifoddbetosaidis Function
The graph of an even function is symmetric about the y-axis.
The graph of an odd function is symmetric about the origin.

23. oddisfunctionthebecausedt
t
t
0
1
3
3 2
3



24. EXAMPLE

25. INTEGRATION OF PIECEWISE FUNCTION
EXAMPLE








4x0,2
2
1
0x2-,2
f(x);)(.1
2
4
2
x
x
dxxf
solution
 
3
56
x2
4
x
3
x
x2
dx2x
2
1
dxx2dx)x(f
4
0
20
2
3
0
2
4
0
2
4
2















  

26. 








6
6
0
0
2-
.
4
2
2
)(.)(.
)()(.
0,2
0,2
)(
int,.1
dxxfddxxfb
dxxfcdxxfa
xifx
xifx
xf
thatgivenegraltheevaluateparteachIn
EXERCISES

27. 








5
10
1
1
0
.
2
1
1
1
)(.)(.
)()(.
1,2
1,2
)(
int,.2
dxxfddxxfb
dxxfcdxxfa
xif
xifx
xf
thatgivenegraltheevaluateparteachIn
EXERCISES

28. b c
Area =0.8
Area =2.6
Area =1.5


d
a
c
b
c
a
b
a
dx)x(f.ddx)x(f.b
f(x)dx.cdx)x(f.a
findtofiguretheinshownareastheUse
d
a

29. Answers :
0.8dx)x(f.a
b
a

2.6dx)x(f.b
c
b

-0.32.6-1.50.8dx)x(f.d
d
a

1.8-2.6-0.8f(x)dx.c
c
a


30. OTHER EXAMPLE
Find the definite integral of the following

31. The mean value theorem for integrals state that somewhere
“between” the inscribed and the circumscribed rectangles there is a
rectangle whose area is precisely equal to the area of the region
under the curve.

32. EXRCISES
Find the value(s) of c guaranteed by the Mean Value Theorem for
Integrals for the function over the given interval.

35. Find the average value of the function over the given interval.
EXRCISES