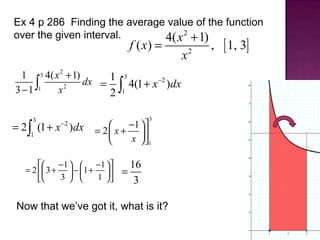
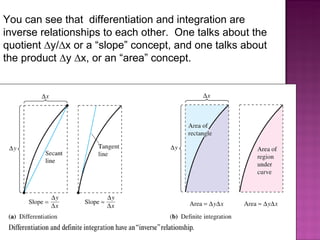
The document discusses several topics related to calculus including: 1) Evaluating definite integrals using the fundamental theorem of calculus. 2) Finding the average value of a function over a closed interval using the mean value theorem. 3) Understanding that differentiation and integration are inverse processes where one deals with slopes and the other with areas.

2. You can see that differentiation and integration are inverse relationships to each other. One talks about the quotient ∆y/∆x or a “slope” concept, and one talks about the product ∆y ∆x, or an “area” concept.

3. Early mathematicians didn’t know that indefinite integration and definite integration were related. But we get to understand the relationship today. Drum roll, please!

4. Guideline #1 is a biggie. Integration requires a rule to apply, and even simple functions sometimes can’t be integrated

5. Ex 1 p 284 Evaluating a definite Integral

6. Ex 2 p284 A definite integral involving absolute value The vertex is (1/2, 0) so split up integral

7. I know it is easy to make little mistakes on this evaluation process. You need to show the integration step , but the evaluation step you can do by calculator unless exact answers are required. Two ways: On main calculator screen: MATH fnInt ( expression, variable, lower limit, upper limit ) On graph screen: Graph function as usual, then select 2 ND CALC, ∫f(x)dx, select lower limit, upper limit, and enter. Both of these can give rounding errors, so know what kind of answers you expect and think accordingly.

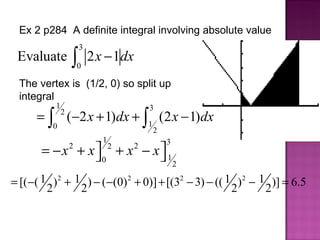
8. Ex 3 p284 Using the Fundamental Theorem for Area Notice that the function lies above the x-axis for interval [0, 1] so result can be thought of as area. Find the area bounded by graph of f(x) = 2x 2 - 3x + 2, y=0, x=0, and x = 1

9. = height x base I imagine the area above f(c) in pink pouring into the blue area to level things out.

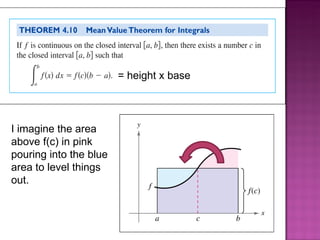
10. The value of f(c) from the Mean Value Theorem ends up being called the Average value of f on the interval [a, b].

11. Ex 4 p 286 Finding the average value of the function over the given interval. Now that we’ve got it, what is it?

12. 4.4a p. 291/ 1-45 every other odd, 47, 49, 55-60