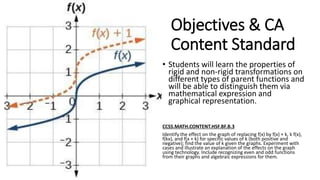
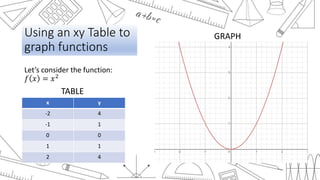
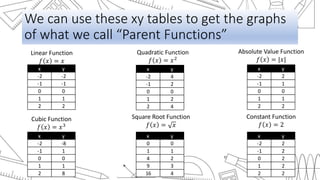
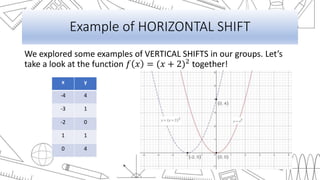
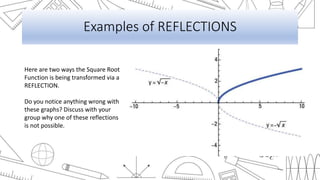
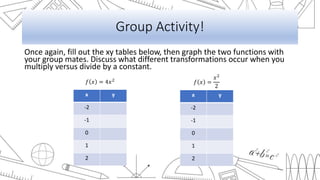
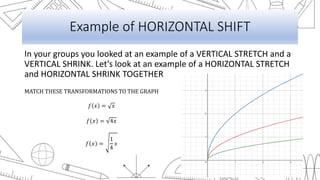
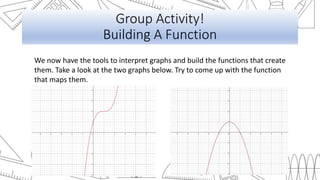
This document discusses transformations of functions, including rigid and non-rigid transformations. Rigid transformations include vertical and horizontal shifts as well as reflections, which change the position of the graph but not its shape. Non-rigid transformations include vertical and horizontal stretches and shrinks, which alter the shape of the graph. Examples of each type of transformation are presented and discussed.

1. Transformations
of Functions
Mr. Johnson
Algebra 1
California Content Standard – Building Functions

2. Objectives & CA
Content Standard
• Students will learn the properties of
rigid and non-rigid transformations on
different types of parent functions and
will be able to distinguish them via
mathematical expression and
graphical representation.
CCSS.MATH.CONTENT.HSF.BF.B.3
Identify the effect on the graph of replacing f(x) by f(x) + k, k f(x),
f(kx), and f(x + k) for specific values of k (both positive and
negative); find the value of k given the graphs. Experiment with
cases and illustrate an explanation of the effects on the graph
using technology. Include recognizing even and odd functions
from their graphs and algebraic expressions for them.

3. Before We Begin, Let’s Recap
What do we know about
functions?
Spend 2-3 minutes
discussing with your
classmates in groups of 4
EVERYTHING you can think
about regarding functions.
We will then write down
one thing from each group
together as a class.

4. Using an xy Table to
graph functions
Let’s consider the function:
𝑓 𝑥 = 𝑥2
TABLE
x y
-2 4
-1 1
0 0
1 1
2 4
GRAPH

5. We can use these xy tables to get the graphs
of what we call “Parent Functions”
x y
-2 -2
-1 -1
0 0
1 1
2 2
x y
-2 4
-1 2
0 0
1 2
2 4
x y
-2 2
-1 1
0 0
1 1
2 2
x y
-2 -8
-1 1
0 0
1 1
2 8
x y
0 0
1 1
4 2
9 3
16 4
x y
-2 2
-1 2
0 2
1 2
2 2
Linear Function
𝑓 𝑥 = 𝑥
Quadratic Function
𝑓 𝑥 = 𝑥2
Absolute Value Function
𝑓 𝑥 = |𝑥|
Cubic Function
𝑓 𝑥 = 𝑥3
Square Root Function
𝑓 𝑥 = 𝑥
Constant Function
𝑓 𝑥 = 2

6. We can use these xy tables to get the graphs
of what we call “Parent Functions”
Linear Function
𝑓 𝑥 = 𝑥
Quadratic Function
𝑓 𝑥 = 𝑥2
Absolute Value Function
𝑓 𝑥 = |𝑥|
Cubic Function
𝑓 𝑥 = 𝑥3
Square Root Function
𝑓 𝑥 = 𝑥
Constant Function
𝑓 𝑥 = 2

7. What happens if we add a one to the function? 𝑓 𝑥 = 𝑥2 + 1
What if we add 5? 𝑓 𝑥 = 𝑥2 + 5
How about if we subtract 2? 𝑓 𝑥 = 𝑥2
− 2
Revisiting the function
𝑓 𝑥 = 𝑥2

8. GROUP ACTIVITY!
• Fill the following xy tables with your group mates and make a
corresponding graph. Discuss with each other any similarities you
have found between these three new quadratic functions and the
parent function.
x y
-2
-1
0
1
2
x y
-2
-1
0
1
2
x y
-2
-1
0
1
2
𝑓 𝑥 = 𝑥2 + 1 𝑓 𝑥 = 𝑥2 + 5 𝑓 𝑥 = 𝑥2 − 2

9. What did you notice?
• This is an example of a RIGID TRANSFORMATION
• A RIGID TRANSFORMATION is a transformation in which the basic shape of
the graph is unchanged
• RIGID TRANSFORMATIONS change only the position of the graph in the
coordinate plane

10. Types of RIGID TRANSFORMATIONS
• There are 3 types of RIGID TRANSFORMATIONS
1. VERTICAL SHIFTS
2. HORIZONTAL SHIFTS
3. REFLECTIONS

11. VERTICAL & HORIZONTAL SHIFTS
Let 𝑐 be some positive real number. We can determine VERTICAL &
HORIZONTAL SHIFTS with the following formulas:
VERTICAL SHIFT 𝑐 units upward:
𝑔 𝑥 = 𝑓 𝑥 + 𝑐
VERTICAL SHIFT 𝑐 units downward:
𝑔 𝑥 = 𝑓 𝑥 − 𝑐
HORIZONTAL SHIFT 𝑐 units to the right:
𝑔 𝑥 = 𝑓(𝑥 − 𝑐)
HORIZONTAL SHIFT 𝑐 units to the left:
𝑔 𝑥 = 𝑓(𝑥 + 𝑐)

12. Example of HORIZONTAL SHIFT
We explored some examples of VERTICAL SHIFTS in our groups. Let’s
take a look at the function 𝑓 𝑥 = (𝑥 + 2)2 together!
x y
-4 4
-3 1
-2 0
1 1
0 4

13. REFLECTIONS
A reflection will reflect your function, like a mirror, over the x or y axis.
We can determine what type of reflection with the following formulas:
Reflection over the x-axis:
𝑔 𝑥 = −𝑓(𝑥)
Reflection over the y-axis:
𝑔 𝑥 = 𝑓(−𝑥)

14. Examples of REFLECTIONS
Here are two ways the Square Root
Function is being transformed via a
REFLECTION.
Do you notice anything wrong with
these graphs? Discuss with your
group why one of these reflections
is not possible.

15. Now let’s look at what happens to the Quadratic Function if we multiply or divide
by some constant 𝑐.
What happens if we multiply by 4? 𝑓 𝑥 = 4𝑥2
What happens if we divide by 2? 𝑓 𝑥 =
𝑥2
2
Revisiting the function
𝑓 𝑥 = 𝑥2

16. Group Activity!
Once again, fill out the xy tables below, then graph the two functions with
your group mates. Discuss what different transformations occur when you
multiply versus divide by a constant.
x y
-2
-1
0
1
2
x y
-2
-1
0
1
2
𝑓 𝑥 = 4𝑥2
𝑓 𝑥 =
𝑥2
2

17. What did you notice?
These types of transformations are called NON-RIGID TRANSFORMATIONS
• A NON-RIGID TRANSFORMATION is a transformation of a graph that
causes a change in the shape of the graph.

18. Types of NON-RIGID TRANSFORMATIONS
• There are 4 types of NON-RIGID TRANSFORMATIONS
1. VERTICAL STRETCH
2. VERTICAL SHRINK
3. HORIZONTAL STRETCH
4. HORIZONTAL SHRINK

19. Stretches and Shrinks
Let 𝑐 be some real number. We can determine VERTICAL &
HORIZONTAL STRETCHES & SHRINKS with the following formulas:
VERTICAL STRETCH:
𝑔 𝑥 = 𝑐𝑓 𝑥 , where 𝑐 > 1
VERTICAL SHRINK:
𝑔 𝑥 = 𝑐𝑓 𝑥 , where 0 < 𝑐 < 1
HORIZONTAL STRETCH:
𝑔 𝑥 = 𝑓(𝑐𝑥), where 𝑐 > 1
HORIZONTAL SHRINK:
𝑔 𝑥 = 𝑓(𝑐𝑥), where 0 < 𝑐 < 1

20. A Useful Tip!
Stretches and Shrinks can be easily confused with one another. Here is
a useful trick to help you remember which is which.
• VERTICAL STRETCH: y-values increased to corresponding x-values
• VERTICAL SHRINK: y-values decreased to corresponding x-values
• HORIZONTAL STRETCH: x-values increased to corresponding y-values
• HORIZONTAL SHRINK: x-values decreased to corresponding y-values

21. Example of HORIZONTAL SHIFT
In your groups you looked at an example of a VERTICAL STRETCH and a
VERTICAL SHRINK. Let’s look at an example of a HORIZONTAL STRETCH
and HORIZONTAL SHRINK TOGETHER
MATCH THESE TRANSFORMATIONS TO THE GRAPH
𝑓 𝑥 = 𝑥
𝑓 𝑥 = 4𝑥
𝑓 𝑥 =
1
4
𝑥

22. Group Activity!
Putting It All Together
It’s possible for a function to undertake more than one
transformation at once. With your group mates, try graphing the
following functions:
𝑓 𝑥 = −2𝑥2+3 𝑓 𝑥 =
1
2
𝑥 + 3 − 2 𝑓 𝑥 = 𝑥 − 2 + 1

23. Group Activity!
Building A Function
We now have the tools to interpret graphs and build the functions that create
them. Take a look at the two graphs below. Try to come up with the function
that maps them.

24. Summary
• We just learned how introducing constants in various ways
can transform a variety of different functions. As you continue
your math career, you will learn about many more parent
functions and these types of transformations will hold for all
of them. This is a key concept that will be important as we
continue to analyze different function topics.