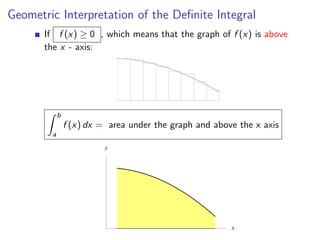
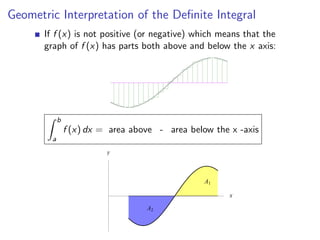
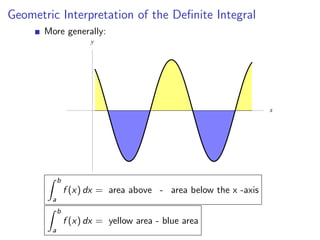
The document defines Riemann sums and definite integrals. Riemann sums approximate the area under a function curve between two points by dividing the interval into subintervals and evaluating the function at sample points in each. The definite integral is defined as the limit of Riemann sums as the number of subintervals approaches infinity. Geometrically, the definite integral represents the net area between the function curve and x-axis over the interval.

1. Riemann Sums
Consider any function f (x) where a ≤ x ≤ b.
b−a
Partition [a, b] into n subintervals of equal length ∆x =
n
Evaluate the function f (x) at sample points c1 , c2 , ... cn
chosen inside each subinterval.
Y
Positive values
a x0 x1 x2 x3 x4 x5 b x6
c1 c2 c3 c4 c5 c6
X
Negative values
Form the Riemann sum:
f (c1 ) · ∆x + f (c2 ) · ∆x + ... + f (cn ) · ∆x

2. Riemann Sum: [f (c1 ) + f (c2 ) + ... + f (cn )] · ∆x
Y
Positive values
a x0 x1 x2 x3 x4 x5 b x6
c1 c3 c4 c5 c6
O c2 X
Negative values

3. The Definite Integral
Notation:
n
f (c1 ) · ∆x + f (c2 ) · ∆x + ... + f (cn ) · ∆x = f (ci ) · ∆x
i=1
Consider more and more subintervals. In other words, let the
number n be larger and larger:
Y
X
Then the limit of the Riemann sums, as the number of
intervals becomes larger and larger is called The Definite
Integral or The Riemann Integral of f (x) from a to b:
b n
f (x) dx = lim f (ci ) ∆x
a n→∞
i=1

4. Geometric Interpretation of the Definite Integral
If f (x) ≥ 0 , which means that the graph of f (x) is above
the x - axis:
b
f (x) dx = area under the graph and above the x axis
a
y
x

5. Geometric Interpretation of the Definite Integral
If f (x) is not positive (or negative) which means that the
graph of f (x) has parts both above and below the x axis:
b
f (x) dx = area above - area below the x -axis
a
y
A1
x
A2

6. Geometric Interpretation of the Definite Integral
More generally:
y
x
b
f (x) dx = area above - area below the x -axis
a
b
f (x) dx = yellow area - blue area
a