The document discusses definite integration and its properties. It defines definite integration as the integration of a continuous function between two fixed limits. Some key properties discussed include:
1) A definite integral is independent of the variable of integration and depends only on the limits.
2) Flipping the limits of integration changes the sign of the integral.
3) Splitting the limits of integration allows breaking the integral into multiple parts summed together.


![1.1. DEFINITE INTEGRATION 3
1Definite Integration
In this chapter, the integration of infinite continuous function is bounded
between two limits.
1.1 Definite Integration
When integration of a function is limited between two fixed points where
function is continuous and limit exists everywhere between these two limits,
then The integral is called definite integration. If f(x) is a continuous func-
tion in [a, b] and limit exists everywhere in [a, b] then definite integration of
the function is given by
I =
b
Z
a
f(x) dx (1.1)
Definite integral depends on lower limit and upper limit only. It is indepen-
dent of any intermediate values between [a, b]. If F(x) is integral of f(x) and
there are intermediate points j, k and l such that [a, j], [j, k], [k, l], [l, b] then
I =
j
Z
a
f(x) dx +
k
Z
j
f(x) dx +
l
Z
k
f(x) dx +
b
Z
l
f(x) dx
and
I = F(j) − F(a) + F(k) − F(j) + F(l) − F(k) + F(b) − F(l) = F(b) − F(a)
It shows that only limits a and b are useful. Rest intermediate points are
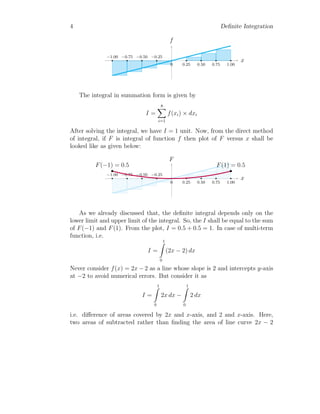
cancelled by each other. Consider a function f(x) = x that is undergoing
integration (bar summation) in [−1, 1]. Take the width dx = 0.25, and
corresponding integral steps n = 8. The bar diagram for integral of f(x) is
given below:](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-3-320.jpg)

![1.2. PROPERTIES 7
Solution Substitute x = s. It gives dx = ds. It converts the integral as
Z
sin x
x
dx =
Z
sin s
s
ds
1.2.2 Flipping of Limits
If a and b > a are lower limit and upper limit respectively for a function f(x),
where it is being integrated then function integration takes place from a to
b. If the direction of integration is change then the integration of function
becomes negative, i.e.
b
Z
a
f(x) dx = −
a
Z
b
f(t) dt
Proof Definite integration of
b
R
a
f(x) dx is
b
Z
a
f(x) dx = F(b) − F(a)
The right hand side of above relation shows that the value of integrated func-
tion F(x) at lower limit a, i.e. F(a) is subtracted in the value of integrated
function F(x) at upper limit b, i.e. F(b). Now take common in right hand
side of above relation
b
Z
a
f(x) dx = −[−F(b) + F(a)]
and it shows that from above description stated, upper limit is a and lower
limit is b. Hence
b
Z
a
f(x) dx = −
a
Z
b
f(x) dx (1.3)](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-7-320.jpg)
![8 Definite Integration
1.2.3 Splitting of Limits
Take, a and b as lower and upper limits for the integral of a function f(x).
If F(x) is integral of f(x) as
Z
f(x) dx = F(x)
and function f(x) is continuous through the region between [a, b]. We can
add a third limit point between boundary limits, a → b, such as a → c → b,
where a < c < b. In this case, integral of the function becomes
b
Z
a
f(x) dx =
c
Z
a
f(x) dx +
b
Z
c
f(x) dx (1.4)
Proof Definite integration of
b
R
a
f(x) dx is
b
Z
a
f(x) dx = F(b) − F(a)
Adding and subtracting function value, F(c), at a point c in above relation
at right side.
b
Z
a
f(x) dx = F(b) − F(a) + F(c) − F(c)
1
1 2
x
y
a b
1
1 2
x
y
a b
c
Figure 1.1: This function is integrated in the closed limit of [a, b]. It rep-
resents area of region enclosed between function and x-axis. Function is
partitioned by splitting limit [a, b] in [a, c] and [c, b]. Area of the region in
limit [a, b] is sum of area of these two regions.](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-8-320.jpg)
![1.2. PROPERTIES 9
Rearranging right hand side of above relation
b
Z
a
f(x) dx = [F(b) − F(c)] + [F(c) − F(a)]
Rewriting right side in integral form:
b
Z
a
f(x) dx =
b
Z
c
f(x) dx +
c
Z
a
f(x) dx
b
Z
a
f(x) dx =
c
Z
a
f(x) dx +
b
Z
c
f(x) dx (1.5)
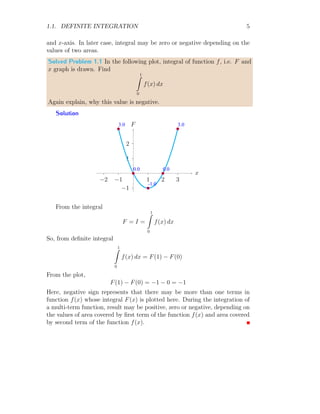
Solved Problem 1.4 Find definite integral of each function as plotted in
following figure.
Solution
1
1 2
t
y
1
1 2 3
t
y
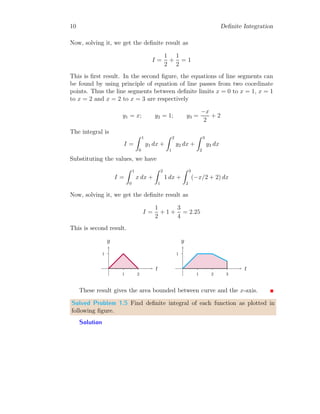
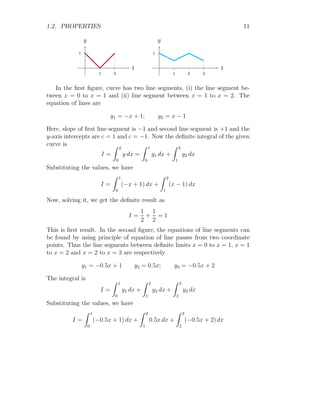
In the first figure, curve has two line segments, (i) the line segment be-
tween x = 0 to x = 1 and (ii) line segment between x = 1 to x = 2. The
equation of lines are
y1 = x; y2 = −x + 2
Here, slope of first line segment is +1 and second line segment is −1 and the
y-axis intercepts are c = 0 and c = 2. Now the definite integral of the given
curve is
I =
Z 2
0
y dx =
Z 1
0
y1 dx +
Z 2
1
y2 dx
Substituting the values, we have
I =
Z 1
0
x dx +
Z 2
1
(−x + 2) dx](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-9-320.jpg)
![12 Definite Integration
Now, solving it, we get the definite result as
I =
3
4
+
3
4
+
3
4
=
9
4
= 2.25
This is second result.
1
1 2
t
y
1
1 2 3
t
y
These result gives the area bounded between curve and the x-axis.
1.2.4 Shifting of Variable
If f(x) is a continuous function in [a, b] and limit exists everywhere in [a, b]
then definite integration of the function is given by
I =
b
Z
a
f(x) dx
Now shift the function by sum of limits, i.e.
x = a + b − t; dx = −dt
The corresponding limits becomes, when x = a, t = b and when x = b, t = a.
So,
I =
a
Z
b
f(a + b − t) × −dt
From the property of flipping of limits, we have
I =
b
Z
a
f(a + b − t) dt](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-12-320.jpg)


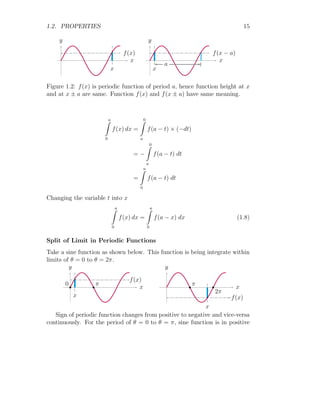
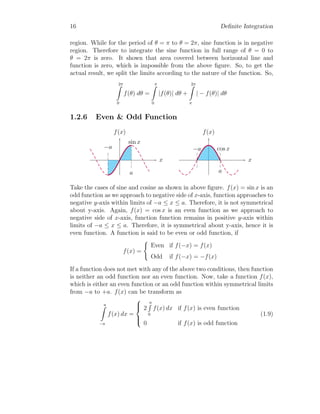


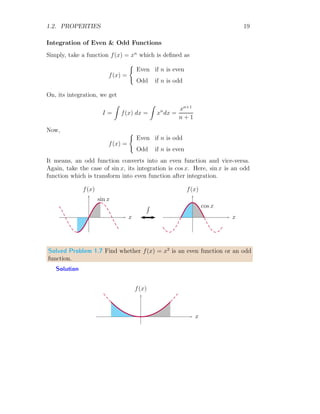






![26 Definite Integration
And its periodic derivation is
I =
π/2
Z
0
p
sin(π/2 − x)
p
sin(π/2 − x) +
p
cos(π/2 − x)
dx
I =
π/2
Z
0
√
cos x
√
cos x +
√
sin x
dx (1.26)
Now adding above two equations
2I =
π/2
Z
0
√
cos x +
√
sin x
√
cos x +
√
sin x
dx
=
π/2
Z
0
1dx
Taking integration and substituting the limits of integration
2I = [x]π/2
0 = π/2
Now solving it we will get the result as
I =
π
4
(1.27)
Solved Problem 1.18 Solve
π/2
R
0
sin2 x
sin x+cos x
dx = 1
√
2
loge(
√
2 + 1).
Solution
Solved Problem 1.19 Solve
π
R
0
x tan x
sec x+tan x
dx = π(π
2
− 1).
Solution The integral is
π
R
0
x tan x
sec x+tan x
dx which is a periodic function in the
interval of θ = 0 to θ = π. Now
I =
π
Z
0
x tan x
sec x + tan x
dx (1.28)](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-26-320.jpg)
![1.2. PROPERTIES 27
And its periodic derivation is
I =
π
Z
0
(π − x) tan(π − x)
sec(π − x) + tan(π − x)
dx
I =
π
Z
0
(π − x) (− tan x)
− sec x − tan x
dx (1.29)
Now adding above two equations
2I =
π
Z
0
π tan x
sec x + tan x
dx
Rationalizing right hand side by multiplying and diving it by sec x − tan x.
2I =
π
Z
0
π tan x(sec x − tan x)
sec2 x − tan2
x
dx
=
π
Z
0
π tan x(sec x − tan x)
1
dx
Opening the bracket to make two parts in right hand side.
2I =
π
Z
0
π tan x · sec x dx −
π
Z
0
tan2
x dx
=
π
Z
0
π tan x · sec x dx −
π
Z
0
(sec2
x − 1) dx
Taking integration and substituting the limits of integration
2I = π [sec x]π
0 − π [tan x − x]π
0
= π [sec π − sec 0] − π [tan π − π − tan 0 + 0]
= π [−1 − 1 − 0 + π + 0 + 0]
= π [π − 2]
Now solving it, we will get the result as
I = π
π
2
− 1
(1.30)](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-27-320.jpg)




![32 Definite Integration
Solved Problem 1.23 A resonance term f(t) = sin(ωt) is derivated twice
with respect to t and then integrated with respect to ω. Find the result.
Solution The given function is
f(t) = sin(ωt)
Its twice derivative about t is given by
f
′′
(t) = −ω2
sin(ωt)
Now, integral is
I =
Z
−ω2
sin(ωt) dω
On integration it with respect to ω, we have
I = −
2tω sin(ωt) + (2 − t2
w2
) cos(ωt)
t3
This is desired result.
1.2.9 Definite Integration Limits
A definite integration of a function f(x) withing bounded region [a, b] is given
by
I =
b
Z
a
f(x) dx
Here, a is lower bound of the function and b is upper bound of the function.
If function f(x) is integrated within symmetric boundaries as
I =
a
Z
−a
f(x) dx
then it can be represented at with limits as
I = lim
ε→a
ε
Z
−ε
f(x) dx](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-32-320.jpg)



![34 Definite Integration
This is desired answer.
1.3 Average Value
We know that
R
f(x) dx represents the Area between function f(x) and two
points of width dx in base line. If
b
Z
a
f(x) dx
is area between f(x) and x-limits (x = a and x = b). The average value for
this limit is given by
Iavg =
b
R
a
f(x) dx
b
R
a
dx
(1.31)
Above relation is similar to the mathematical average, i.e. average area is
the ratio of total area to the difference of limit.
Solved Problem 1.25 Find the average value of constant ‘c’ for the limits
ranges from t = a to t = b.
Solution The average value of function f(t) is given by
Iavg =
b
R
a
c dt
b
R
a
dt
t
c b b
c c
b b
a b
Now
Iavg = c
[t]b
a
[t]b
a](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-36-320.jpg)
![1.3. AVERAGE VALUE 35
Solving the relation
Iavg = c
This shows that the average value of constant remains constant.
Solved Problem 1.26 Find the average value of f(t) = t2
for the t-limits
ranges from t = a to t = b.
Solution The average value of function f(t) is given by
Iavg =
b
R
a
t dt
b
R
a
dt
t
f(t)
b
b
f(a)
f(b)
b b
a b
t line
Now
Iavg =
h
t2
2
ib
a
[t]b
a
Solving the relation
Iavg =
1
2
(a + b)
This shows that the average values of a line is average of sum of two ends of
the line.
Solved Problem 1.27 Find the average value of f(x) = x2
for the x-limits
ranges from x = 2 to x = 3.
Solution From the average relation
Iavg =
b
R
a
f(x) dx
b
R
a
dx](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-37-320.jpg)
![36 Definite Integration
x
f(x)
b
b
f(a)
f(b)
b b
a b
f(x) = x2
Substituting the values and integrating for the limits
Iavg =
3
R
2
x2
dx
3
R
2
dx
Or
Iavg =
h
x3
3
i3
2
[x]3
2
Or
Iavg =
19
3
This is the required average value.
Solved Problem 1.28 Find the average value of f(x) = sin(x) within the
angle limits in radian values from x = π/3 to 2π/3.
Solution The average of function within the limits is
Iavg =
2π
3
R
π
6
sin(x)dx
2π
3
R
π
6
dx
On integration and solving it
Iavg =
[− cos(x)]
2π
3
π
6
[x]
2π
3
π
6](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-38-320.jpg)

![38 Definite Integration
Solution Integration of given function is
I =
2
Z
−4
f(x) dx
Replacing the function f(x) for its domain of ‘x’
I =
0
Z
−4
2 dx +
2
Z
0
x dx
On solving it
I = [2x]0
−4 +
x2
2
2
0
Or
I = 10
Solved Problem 1.30 Find the integral of the given function in −∞ x
∞.
f(x) =
(
x − 1 if − 1 ≤ x ≤ 0
0 otherwise
Solution
1
−1
−2
1
−1
−2
x
f(x)
1
−1
−2
1
−1
−2
x
F(x)](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-40-320.jpg)
![40 Definite Integration
On solving it
I = 0 + [x]∞
2
Or
I = ∞
Ans-1.
2. Integration of e−at
u(t − 2) is
I =
∞
Z
0
e−at
u(t − 2) dt
Replacing the unit step function u(t − 2) for its domain of ‘t’
I =
2
Z
0
e−at
× 0 dt +
∞
Z
2
e−at
× 1 dt
On solving it
I = 0 +
e−at
−a
∞
2
Or
I =
e−2a
a
Ans-2.
By this way, we can obtain the Laplace Transformations of unit step
function also. Second derivative is very important in engineering.
Solved Problem 1.32 Check whether the given piece-wise function exists or
not.
f(t) =
(
2t if 0 ≤ t ≤ 1
t + 1 if 1 ≤ t ≤ 2
Also find the
∞
R
−∞
f(t) dt.
Solution Function is critical for both piece-wise parts at t = 1. Therefore,
at this point, function should be continuous for its existence. So
f(t)−
= 2 × 1 = 2](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-42-320.jpg)
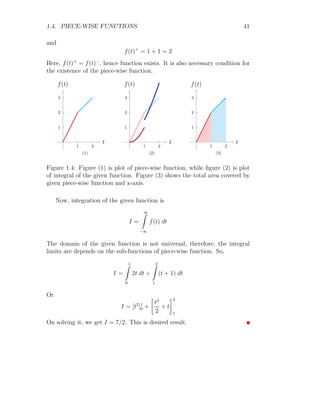
![1.4. PIECE-WISE FUNCTIONS 41
and
f(t)+
= 1 + 1 = 2
Here, f(t)+
= f(t)−
, hence function exists. It is also necessary condition for
the existence of the piece-wise function.
1
2
3
1 2
t
f(t)
(1)
1
2
3
1 2
t
f(t)
(2)
1
2
3
1 2
t
f(t)
(3)
Figure 1.4: Figure (1) is plot of piece-wise function, while figure (2) is plot
of integral of the given function. Figure (3) shows the total area covered by
given piece-wise function and x-axis.
Now, integration of the given function is
I =
∞
Z
−∞
f(t) dt
The domain of the given function is not universal, therefore, the integral
limits are depends on the sub-functions of piece-wise function. So,
I =
1
Z
0
2t dt +
2
Z
1
(t + 1) dt
Or
I = [t2
]1
0 +
t2
2
+ t
2
1
On solving it, we get I = 7/2. This is desired result.](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-43-320.jpg)













![1.6. SPECIAL INTEGRAL 51
f(t) is a positive function of t and s is a constant variable, then integral of
type
Ilapace = L[f(t)] =
∞
Z
0
f(t)e−st
dt (1.34)
is known as Laplace integral and method is called Laplace Transformation.
Transformation word is used as old variable t is transformed into new vari-
able s, i.e. the function is transform from time domain (say t domain) into
frequency domain (say s domain). Here e−st
is Laplace operator, i.e. inte-
gral kernel and f(t) is operand. Old and new variable may be denoted by
other alphabetic letters and it does not matter in our solutions. In Laplace
transform, eat
is known as shift operator. If a is positive then s is shifted
leftward, i.e. s + a. Similarly, if a is negative then s is shifted rightward, i.e.
s + a.
Solved Problem 1.42 Find the integral of e−at
with respect to t within limits
from t = 0 to t = ∞. Also find the integral value when a → ∞.
Solution From the given problem
I =
∞
Z
0
e−at
dt =
e−at
−a](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-57-320.jpg)








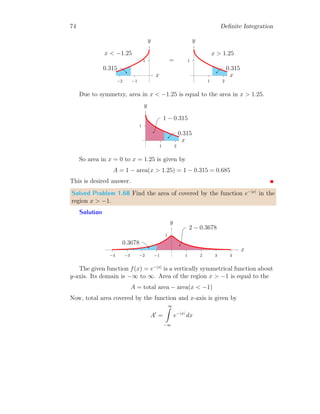
![1.6. SPECIAL INTEGRAL 53
I2 =
∞
Z
0
te−at
dt =
−
(at + 1)e−at
a2
∞
0
=
1
a2
I3 =
∞
Z
0
t2
e−at
dt =
−
(a2
t2
+ 2at + 2)e−at
a3
∞
0
=
2
a3
From these three results, we find that the integral values are in order of
In =
n!
an+1
Where, n is power of t and is an integer. So, the
∞
Z
0
tn
e−at
dt =
n!
an+1
This is desire result.
Solved Problem 1.45 Let κ is an operator which means
κ[f(x)] =
t
Z
0
f(x) dx
Now, find the value of κ sin x and κ2
sin x.
Solution The given relation is
κ[f(x)] =
t
Z
0
f(x) dx
Now, substituting the value of f(x) = sin x, we have
κ[sin x] =
t
Z
0
sin x dx = [− cos x]t
0
It gives κ[sin x] = 1 − cos t. Now, κ2
[sin x] can be written as κ [κ[sin x]].
Therefore, f(x) becomes κ[sin x] and its value is 1 − cos x, (t is replaced by](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-67-320.jpg)
![54 Definite Integration
x). Now
κ2
[sin x] =
t
Z
0
(1 − cos x) dx = [x − sin x]t
0
It gives κ2
[sin x] = t − sin t.
Solved Problem 1.46 Find the value of
R ∞
0
e−x2
dx.
Solution To find the integral of this problem, substitute x2
= t. The
corresponding 2x dx = dt. Now, when x = 0, t = 0 and when x = ∞, t = ∞.
The integral becomes
I =
Z ∞
0
t−1/2
e−t
dt
2
Or
I =
1
2
Z ∞
0
t
1
2
−1
e−t
dt =
1
2
× Γ
1
2
This gives I =
√
π/2.
1.6.2 Definite Integral of Fourier Type
We know that Laplace type integral of a function is given by
IL =
∞
Z
0
f(x)e−sx
dx
in s-domain or time domain. If s is replaced iω or jω (where i2
= −1 or
j2
= −1) then integral becomes Fourier type.
IF =
∞
Z
0
f(x)e−iωx
dx (1.35)
Where ω = 2πf in frequency domain. Laplace type integral is related with
Fourier type integral by s ←→ iω. For complete Fourier transform
IF =
∞
Z
−∞
f(x)e−iωx
dx (1.36)](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-68-320.jpg)

![56 Definite Integration
Solved Problem 1.48 Find the constant value of Fourier series integration of
the given function f(x) = sin x within limits from 0 to π.
Solution Constant term a0 in the Fourier series integration is given by
a0 =
1
b − a
b
Z
a
f(x) dx
Taking limits from 0 to π and function f(x) = sin x, the Fourier series con-
stant integral term becomes to
a0 =
1
π − 0
π
Z
0
sin x dx
Or
a0 =
1
π
[− cos x]π
0
It gives a0 = 2/π.
Solved Problem 1.49 Find the constant value of Fourier series integration of
the given function f(x) = x sin x within limits from 0 to π.
Solution Constant term a0 in the Fourier series integration is given by
a0 =
1
b − a
b
Z
a
f(x) dx
Taking limits from 0 to π and function f(x) = x sin x, the Fourier series
constant integral term becomes to
a0 =
1
π − 0
π
Z
0
x sin x dx
Or
a0 =
1
π
[sin x − x cos x]π
0
It gives a0 = 1.](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-70-320.jpg)
![1.6. SPECIAL INTEGRAL 57
Solved Problem 1.50 Find the constant value of Fourier series integration of
the given function f(x) = x2
within limits from 0 to π.
Solution Constant term a0 in the Fourier series integration is given by
a0 =
1
b − a
b
Z
a
f(x) dx
Taking limits from 0 to π and function f(x) = x2
, the Fourier series constant
integral term becomes to
a0 =
1
π − 0
π
Z
0
x2
dx
Or
a0 =
1
π
x3
3
π
0
It gives a0 = π2
/3.
1.6.3 Specific Workout
In the following section, we do and find the definite integral by applying
conditions and will analysis our answers.
Solved Problem 1.51 Find the definite integration of f(x) = sin x within
limits from 0 to π/2. What would the answer if function is multiplied by x?
Solution The definite integral as per given problem is
I =
π/2
Z
0
sin x dx = [− cos x]π/2
0 = [− cos(π/2)] − [− cos 0]
This gives I = 1. Now, function is multiplied by x. So, new integral be
I′
=
π/2
Z
0
x × sin x dx = [x × − cos x]π/2
0 −
π/2
Z
0
d
dx
x
Z
sin x dx
dx](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-71-320.jpg)
![58 Definite Integration
On simplification
I′
=
hπ
2
× − cos(π/2)
i
− [0 × − cos 0] −
π/2
Z
0
[− cos x] dx
Or
I′
= [sin x]π/2
0
It gives, I′
= 1. Thus both results are same.
Solved Problem 1.52 Find the definite integration of f(x) = cos x within
limits from 0 to π/2. What would the answer if function is multiplied by x?
Solution The definite integral as per given problem is
I =
π/2
Z
0
cos x dx = [sin x]π/2
0 = [sin(π/2)] − [sin 0]
This gives I = 1. Now, function is multiplied by x. So, new integral be
I′
=
π/2
Z
0
x × cos x dx = [x × sin x]π/2
0 −
π/2
Z
0
d
dx
x
Z
cos x dx
dx
On simplification
I′
=
hπ
2
× sin(π/2)
i
− [0 × sin 0] −
π/2
Z
0
[sin x] dx
Or
I′
=
π
2
− 0 − [− cos x]π/2
0 =
π
2
+ cos(π/2) − cos 0
It gives, I′
= π
2
− 1. Thus both results are not same.
Solved Problem 1.53 Find the definite integration of f(x) = 1
1+x2 within
limits from 0 to ∞. What would the answer if function is multiplied by x?
Solution The definite integral as per given problem is
I =
∞
Z
0
1
1 + x2
dx =
tan−1
x
∞
0
=
tan−1
∞
−
tan−1
0](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-72-320.jpg)
![1.6. SPECIAL INTEGRAL 59
This gives I = π/2. Now, function is multiplied by x. So, new integral be
I′
=
∞
Z
0
x
1 + x2
dx
Put 1 + x2
= t. On differentiation, it gives, 2x dx = dt. Or it gives x dx =
dt/2. The corresponding limits are t = 1 to t = ∞ respectively when x = 0
and x = ∞. On simplification
I′
=
1
2
×
∞
Z
1
1
t
dt
Or
I′
=
1
2
× [ln t]∞
1
It gives that I′
is divergent in the given region of x. So, indefinite integral will
be found by substituting the value of t and neglecting the limits of integration
and adding a constant.
I′
=
ln(1 + x2
)
2
+ C
Solved Problem 1.54 Find the definite integration of f(k) = e−sk
within
limits from 0 to ∞. Here s is a constant. What would the answer if function
is multiplied by k?
Solution The definite integral as per given problem is
I =
∞
Z
0
e−sk
dk =
1
−s
×
e−sk
x
∞
0
=
1
−s
×
e−s×∞
− e−s×0
If s 0 then e−s×∞
will be equal to zero. If s 0 say s = −ǫ then e−s×∞
will be equal to eǫ×∞
and it will be equal to ∞. Second case is not acceptable
as integral in divergent, so taking first case (s 0) only, we have I = 1/s.
Now, function is multiplied by k. So, new integral be
I′
=
∞
Z
0
ke−sk
dk](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-73-320.jpg)
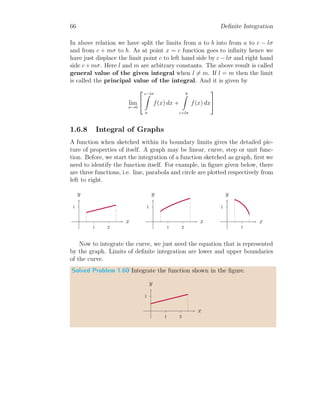
![1.6. SPECIAL INTEGRAL 61
Again integrating second part of above relation
I = f(x) G(x)±
f
′
(x)
Z
G(x) dx ±
Z
d
dx
f
′
(x) ×
Z
G(x) dx
dx
(1.44)
on solving
I = f(x) G(x) ±
f
′
(x) g(x) ±
Z
f(x) × g(x) dx
(1.45)
R
f(x) × g(x) dx is equal to I, hence above equation can be written as
I = f(x) G(x) ± f
′
(x) g(x) ± I (1.46)
Here, sign of I in right hand side is determinant. It may cancel to I in left
side or may added to it. Let the coefficient of I is k. So,
kI = f(x) G(x) ± f
′
(x) g(x) (1.47)
Here k is constant and integral solution I can be obtained by dividing right
hand side by k. ± is used to describe method of finding integral step by step.
Next is the solved problem that explains this method step by step.
Solved Problem 1.55 Find the integral of ex
sin(x).
Solution Let
I =
Z
ex
sin(x) dx
Using product rule, we have
I = ex
Z
sin(x) dx −
Z
d
dx
ex
×
Z
sin(x) dx
dx
On simplification, we have
I = ex
× − cos(x) −
Z
[ex
× − cos(x)] dx
Again solving the second part of right hand side:
I = −ex
cos(x) +
ex
Z
cos(x) dx −
Z
d
dx
ex
Z
cos x dx
dx](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-75-320.jpg)
![62 Definite Integration
On simplification
I = −ex
cos(x) + ex
sin(x) −
Z
ex
sin x dx
Or
2I = ex
(sin x − cos x)
Or
I =
ex
2
(sin x − cos x)
This is required result.
1.6.5 Derivative of Integrals
Let a continuous and differentiable function f(x) whose anti-derivative is
F(x) and derivative of F(x) is f(x) within the definite limits from a to b.
Here a b are the function of t. Now the integral is
b
Z
a
f(x) dx = F(a) − F(b)
Now derivative of the given function with respect to t is
d
dt
b
Z
a
f(x) dx =
d
dt
[F(b) − F(a)]
= f(b) ·
d
dt
b − f(a) ·
d
dt
a
Or
d
dt
b
Z
a
f(x) dx
= f(b) ·
db
dt
− f(a) ·
da
dt
(1.48)
This is the derivative of a function under the sign of definite integral.
Solved Problem 1.56 Evaluate the relation
d
dx
x2
Z
0
sin(t) dt](https://image.slidesharecdn.com/definiteintegral-211202172103/85/Definite-Integral-76-320.jpg)
