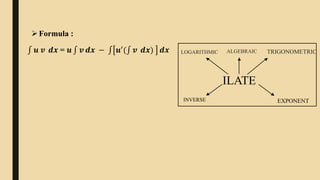
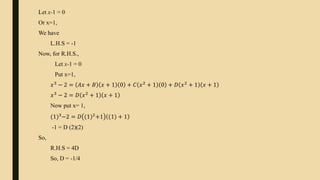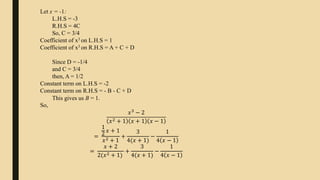The document provides an overview of calculus and analytical geometry presented by Group D. It discusses various topics related to integration including the history and development of integration, the definition and purpose of integration, common integration rules and formulas like integration by parts and integration by partial fractions, and real-life applications of integration in fields like engineering, medicine, and physics. Examples are provided to demonstrate how to use integration techniques like integration by parts and integration by partial fractions to evaluate definite integrals.

1. CALCULUS AND ANALYTICAL GEOMETRY
Presented by:
Group D

2. Muhammad Ali Siddique 20021519-073
Mahnoor Nasir 20021519-106
Rafia Rasool 20021519-064
Rimsha Nisar 20021519-027
Jahanzaib Nasir 20021519-118

3. • Integration by Parts
• Integration by Partial Fractions
Topics:

4. What is
Integration?
The integration is the process of finding the
antiderivative of a function. The integration is the inverse
process of differentiation. Basically, the process of
finding integrals is called integration.

5. ■ The path to the development of the integral is a branching
one, where similar discoveries were made simultaneously
by different people. The history of the technique that is
currently known as integration began with attempts to
find the area underneath curves. The foundations for the
discovery of the integral were first laid by Cavalieri, an
Italian Mathematician, in around 1635.
History of Integration:

6. Along with differentiation, integration is a fundamental
operation of calculus, and serves as a tool to solve problems in
mathematics and physics involving the area of an arbitrary shape,
the length of a curve, and the volume of a solid, among others.
Why we need Integration?

7. Rules
Function Integral
Multiplication by constant ∫cf(x) dx c∫f(x) dx
Power Rule (n≠-1) ∫xn dx
xn+1
n+1
+ C
Sum Rule ∫(f + g) dx ∫f dx + ∫g dx
Difference Rule ∫(f - g) dx ∫f dx - ∫g dx
Rules:

8. Applications of Integration in Real life:
 Application in Engineering:
In Electrical Engineering, Calculus (Integration) is used to determine the exact length of
power cable needed to connect two substations, which are miles away from each other.
 Application in Medical Science:
Biologists use differential calculus to determine the exact rate of growth in a bacterial
culture when different variables such as temperature and food source are changed.
 Application in Physics:
1. In Physics, Integration is very much needed. For example, to calculate the Centre
of Mass, Centre of Gravity and Mass Moment of Inertia of a sports utility vehicle.
2. To calculate the velocity and trajectory of an object, predict the position of planets,
and understand electromagnetism.

9. • Integration by Parts
• Integration by Partial Fraction
• Trigonometric Substitution
• U-substitution
• Integration Using Trigonometric Identities
• Reverse Chain Rule
Types of Integration

10.  Integration by Parts
 Integration by part is a method for evaluating the
different integral when the integral is a product of
functions, the integration by parts formula moves the
product out of the equals so the integrals can also be
solved more easily.
 Invented by:
Mathematician Brook Taylor discovered integration by parts, first publishing the idea
in 1715. More general formulations of integration by parts exist for the Riemann–
Stieltjes and Lebesgue–Stieltjes integrals.
Integration by parts is often used in harmonic analysis, particularly Fourier analysis,
to show that quickly oscillating integrals with sufficiently smooth integrands decay
quickly. The most common example of this is its use in showing that the decay of
function's Fourier transform depends on the smoothness of that function.
 Uses:

11. Formula :
𝒖 𝒗 ⅆ𝒙 = 𝒖 𝒗 ⅆ𝒙 − 𝒖′
( 𝒗 ⅆ𝒙) ⅆ𝒙
ILATE
INVERSE
LOGARITHMIC ALGEBRAIC TRIGONOMETRIC
EXPONENT

12.  ∫x cos x dx.
Example 1
By using formula,
𝒖 𝒗 ⅆ𝒙 = 𝒖 𝒗 ⅆ𝒙 − 𝒖′
( 𝒗 ⅆ𝒙) ⅆ𝒙
∫ x cos x dx = x sin x - ∫ 1.sin x dx
= x sin x – (-cos x)
= x sin x + cos x + C
Example 2
 ∫ln x dx.
Let
∫ln x dx = ∫ln x.1 dx.
By using formula,
𝒖 𝒗 ⅆ𝒙 = 𝒖 𝒗 ⅆ𝒙 − 𝒖′
( 𝒗 ⅆ𝒙) ⅆ𝒙
∫ln x.1 dx= ln x(x) -∫
1
𝑥
. x dx
= x ln x - ∫ 1 dx
= x ln x – x + C

13.  𝑥2𝑒𝑥𝑑𝑥.
Example 3
By using formula,
𝒖 𝒗 ⅆ𝒙 = 𝒖 𝒗 ⅆ𝒙 − 𝒖′( 𝒗 ⅆ𝒙) ⅆ𝒙
∫ x2 ex dx= x2 ex - ∫ 2x. ex dx
= x2 ex - 2∫ x. ex dx
Again integrating by parts, we get
∫ x. ex dx = x. ex - ∫ 1. ex dx
=x. ex - ex
So, now we have
= x2 ex – 2 (x. ex – ex) +C
= x2 ex – 2 x ex + 2ex +C

14.  Integration by Partial Fractions
 This process of taking a rational expression and decomposing it into simpler rational
expressions that we can add or subtract to get the original rational expression is
called partial fraction decomposition. Many integrals involving rational expressions
can be done if we first do partial fractions on the integrand.
The concept was discovered independently in 1702 by both Johann Bernoulli and
Gottfried Leibniz.
 Invented By:
 Factors:
Partial fractions can only be done if the degree of the numerator is strictly less than the
degree of the denominator. That is important to remember.

15. Factors:
Denominator containing… Expression Form of Partial Fractions
a. Linear factor
𝑓 𝑥
(𝑥 + 𝑎)(𝑥 + 𝑏)
𝐴
𝑥 + 𝑎
+
𝐵
𝑥 + 𝑏
a. Repeated Linear factors
𝑓 𝑥
(𝑥 + 𝑎)3
𝐴
𝑥 + 𝑎
+
𝐵
(𝑥 + 𝑎)2
+
𝐶
(𝑥 + 𝑎)3
a. Quadratic term
(which cannot be factored)
𝑓 𝑥
(𝑎𝑥2 + 𝑏𝑥 + 𝑐)(𝑔𝑥 + ℎ)
𝐴𝑥 + 𝐵
𝑎𝑥2 + 𝑏𝑥 + 𝑐
+
𝐶
(𝑔𝑥 + ℎ)

16. Express the following in partial fractions.
𝟑𝒙
(𝟐𝒙+𝟏) 𝒙+𝟒
We set,
3𝑥
(2𝑥 + 1) 𝑥 + 4
=
𝐴
2𝑥 + 1
+
𝐵
𝑥 + 4
We find the values of A and B by multiplying both sides by (2x + 1)(x + 4)
3𝑥 = 𝐴 𝑥 + 4 + 𝐵(2𝑥 + 1)
Then we expand and collect like terms:
3𝑥 = (𝐴 + 2𝐵)𝑥 + (4𝐴 + 𝐵)
Next, we equate x and constant terms:
The x terms gives: 3= A + 2B (i)
The constant terms give: 0 = 4A + B (ii)
Linear Factors Example:

17. Solving this set of simultaneous equations gives:
From eq (ii),
𝐴 = −
𝐵
4
Now put the value of A in (i),
3= −
𝐵
4
+ 2B
Or 3 =
−𝐵+8𝐵
4
7𝐵
4
= 3
𝐵 =
12
7
Similarly, put value of B in (ii), we get
0 = 4A +
12
7
−
12
7
= 4A
−
12
28
= A
𝐴 = −
3
7
So,
3𝑥
(2𝑥 + 1) 𝑥 + 4
=
−3
7 2x + 1
+
12
7(x + 4)

18. Repeated Linear Factors Example:
Express the following as a sum of partial fractions.
𝒙+𝟓
𝒙+𝟑 𝟐
𝑥 + 5
𝑥 + 3 2
=
𝐴
𝑥 + 3
+
𝐵
𝑥 + 3 2
Multiply both sides by (x + 3)2
𝑥 + 5 = 𝐴 𝑥 + 3 + 𝐵
𝑥 + 5 = 𝐴𝑥 + 3𝐴 + 𝐵
By comparing value of x,
1 = 𝐴
Now by comparing values of constants,
5 = 3𝐴 + 𝐵
5 = 3(1) + 𝐵 ∴By putting A=1
So, B = 2.
So,
𝑥 + 5
𝑥 + 3 3
=
1
𝑥 + 3
+
2
𝑥 + 3 2

19. Denominator Containing a Quadratic Factor Example:
Express the following as a sum of partial fractions.
𝒙𝟑−𝟐
𝒙𝟒−𝟏
Firstly, we need to factor the denominator. We just use difference of 2 squares, twice:
𝑥4
− 1 = 𝑥2
+ 1 𝑥2
− 1 = 𝑥2
+ 1 𝑥 + 1 𝑥 − 1
So,
𝑥3 − 2
𝑥4 − 1
=
𝑥3 − 2
𝑥2 + 1 𝑥 + 1 𝑥 − 1
The partial fraction decomposition will be of the form:
𝑥3
− 2
𝑥2 + 1 𝑥 + 1 𝑥 − 1
=
𝐴𝑥 + 𝐵
𝑥2 + 1
+
𝐶
𝑥 + 1
+
𝐷
𝑥 − 1
We multiply throughout by 𝑥2
+ 1 𝑥 + 1 𝑥 − 1
𝑥3
− 2 = 𝐴𝑥 + 𝐵 𝑥 + 1 𝑥 − 1 + 𝐶 𝑥2
+ 1 𝑥 − 1 + 𝐷 𝑥2
+ 1 𝑥 + 1 …. (i)

20. Let x-1 = 0
Or x=1,
We have
L.H.S = -1
Now, for R.H.S.,
Let x-1 = 0
Put x=1,
𝑥3
− 2 = 𝐴𝑥 + 𝐵 𝑥 + 1 0 + 𝐶 𝑥2
+ 1 0 + 𝐷 𝑥2
+ 1 𝑥 + 1
𝑥3
− 2 = 𝐷 𝑥2
+ 1 𝑥 + 1
Now put x= 1,
(1)3
−2 = 𝐷 (1)2
+1 (1) + 1
-1 = D (2)(2)
So,
R.H.S = 4D
So, D = -1/4

21. Let x = -1:
L.H.S = -3
R.H.S = 4C
So, C = 3/4
Coefficient of x3 on L.H.S = 1
Coefficient of x3 on R.H.S = A + C + D
Since D = -1/4
and C = 3/4
then, A = 1/2
Constant term on L.H.S = -2
Constant term on R.H.S = - B - C + D
This gives us B = 1.
So,
𝑥3
− 2
𝑥2 + 1 𝑥 + 1 𝑥 − 1
=
1
2
𝑥 + 1
𝑥2 + 1
+
3
4(𝑥 + 1)
−
1
4 𝑥 − 1
=
𝑥 + 2
2(𝑥2 + 1)
+
3
4(𝑥 + 1)
−
1
4 𝑥 − 1

22.  Thomas calculus 13th edition.
References:
 https://en.wikipedia.org/wiki/Integral