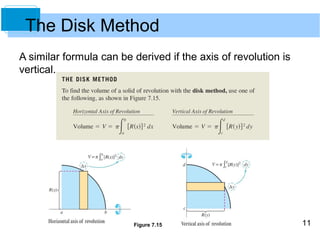
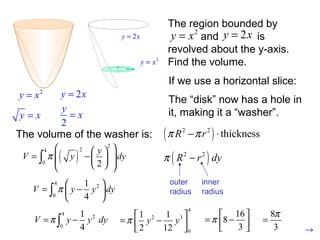
1) The document provides instructions for calculating the volume of a cylinder given its height and total volume. It defines a cylinder as a solid of revolution formed by rotating a rectangle about an axis. 2) The volume of a cylinder (solid of revolution formed by a disk) is calculated using the formula: Volume = πR2w, where R is the radius and w is the width (height) of the disk. 3) Examples are provided to demonstrate calculating the volume of solids of revolution using the disk method, which treats the solid as a series of thin circular disks and sums their individual volumes.

1. AP Calculus Warm up
A cylinder has a height of 9 feet and a volume of 706.5 cubic
feet.
Find the radius of the cylinder. Use 3.14 for π .

2. The Disk Method
If a region in the plane is revolved about a line, the resulting
solid is a solid of revolution, and the line is called the axis
of revolution.
The simplest such solid is a right
circular cylinder or disk, which is
formed by revolving a rectangle
about an axis adjacent to one
side of the rectangle,
as shown in Figure 7.13.
Figure 7.13
2

3. The Disk Method
The volume of such a disk is
Volume of disk = (area of disk)(width of disk)
= πR2w
where R is the radius of the disk and w is the width.
3

4. 7.3 day 2
Disk and Washer Methods
Limerick Nuclear Generating Station, Pottstown, Pennsylvania
Photo by Vickie Kelly, 2003
Greg Kelly, Hanford High School, Richland, Washington

5. y= x
Suppose I start with this curve.
My boss at the ACME Rocket
Company has assigned me to
build a nose cone in this shape.
So I put a piece of wood in a
lathe and turn it to a shape to
match the curve.
→

6. Lathe

7. y= x
How could we find the volume
of the cone?
One way would be to cut it into a
series of thin slices (flat cylinders)
and add their volumes.
The volume of each flat
cylinder (disk) is:
π r 2 ⋅ the thickness
π
( x)
2
dx
In this case:
r= the y value of the function
thickness = a small change
in x = dx
→

8. y= x
The volume of each flat
cylinder (disk) is:
π r 2 ⋅ the thickness
π
( x)
2
dx
If we add the volumes, we get:
∫ π(
4
x
0
)
2
dx
4
= ∫ π x dx
0
4
π 2
= x
2 0
= 8π
→

9. This application of the method of slicing is called the
disk method. The shape of the slice is a disk, so we
use the formula for the area of a circle to find the
volume of the disk.

10. The Disk Method
This approximation appears to become better and better
as
So, you can define the volume of the
solid as
Volume of solid =
Schematically, the disk method looks like this.
10

11. The Disk Method
A similar formula can be derived if the axis of revolution is
vertical.
Figure 7.15
11

12. Example 1 – Using the Disk Method
Find the volume of the solid formed by revolving the region
bounded by the graph of
and the x-axis
(0 ≤ x ≤ π) about the x-axis.
Solution:
From the representative
rectangle in the upper graph
in Figure 7.16, you can see that
the radius of this solid is
R(x) = f(x)
12
Figure 7.16

13. Example 1 – Solution
cont’d
So, the volume of the solid of revolution is
13

14. Example 2 –
Revolving about a line that is not the coordinate axis.
 Find the volume of the solid formed by revolving the
f ( x) = 2 − x 2 and g ( x) = 1 about the
region bounded by:
line: y = 1
14

15. Example 1: (Use Graphing Calculator)
Find the volume of the solid formed by revolving the region
bounded by the graph of f ( x) = .5 x 2 + 4 and the x-axis,
between x = 0 and x = 3, about the x-axis.
Example 2: (No calculator) Rotate the region below
About the y- axis.
Example 3: (Use technology) rotate the region Bounded by the
x2
Graphs of y = 2 , and f ( x) = 4 −
about the line y = 2
4
15

16. 1
The region between the curve x = y , 1 ≤ y ≤ 4 and the
y-axis is revolved about the y-axis. Find the volume.
y
1
We use a horizontal disk.
x
1
3
1
= .707
2
1
= .577
3
4
1
2
2
The thickness is dy.
dy
The radius is the x value of the
1
function =
.
y
2
 1 
V =∫ π
dy
 y

1


4
=∫ π
4
1
1
dy
y
volume of disk
0
= π ln y 1 = π ( ln 4 − ln1)
4
= π ln 22 = 2π ln 2
→

17. y
The natural draft cooling tower
shown at left is about 500 feet
high and its shape can be
approximated by the graph of
this equation revolved about
the y-axis:
500 ft
x
x = .000574 y 2 − .439 y + 185
The volume can be calculated using the disk method with
a horizontal disk.
π∫
500
0
( .000574 y
2
− .439 y + 185 ) dy ≈ 24, 700, 000 ft 3
2
→

18. y = 2x
y = x2
The region bounded by
y = x 2 and y = 2 x is
revolved about the y-axis.
Find the volume.
If we use a horizontal slice:
y = 2x
y
=x
2
y = x2
y=x
The “disk” now has a hole in
it, making it a “washer”.
The volume of the washer is:

V =∫ π
0


4
( y)
2
 y
− 
2
2

 dy


1 2

V = ∫ π  y − y  dy
0
4 

4
V =π∫
4
0
1 2
y − y dy
4
( π R − π r ) ⋅ thickness
π ( R − r ) dy
2
2
2
2
outer
radius
4
1 
1
= π  y2 − y3 
12  0
2
inner
radius
 16 
= π 8 − 
3

8π
=
3
→

19. This application of the method of slicing is called the
washer method. The shape of the slice is a circle
with a hole in it, so we subtract the area of the inner
circle from the area of the outer circle.
The washer method formula is:
b
V = π ∫ R 2 − r 2 dx
a
Like the disk method, this formula will not be on the
formula quizzes. I want you to understand the formula.
→

20. y = x2
y = 2x
r
y = 2x
y
=x
2
y = x2
y=x
r = 2− y
y2
= π ∫ 4 − 2 y + − 4 + 4 y − y dy
0
4
1
4
1 2
= π ∫ −3 y + y + 4 y 2 dy
0
4
4
V = π ∫ R 2 − r 2 dy
0
2
(
y

=π ∫ 2−  − 2− y
0
2

)
2
dy
(
)
4
 3 2 1 3 8 
= π ⋅ − y + y + y 
12
3 0
 2
16 64 
8π

= π ⋅  −24 + +  =
3 3
3

3
2

y2 
= π ∫  4 − 2 y +  − 4 − 4 y + y dy
0
4 

4
The outer radius is:
y
R = 2−
2
The inner radius is:
R
4
4
If the same region is
rotated about the line x=2:
π