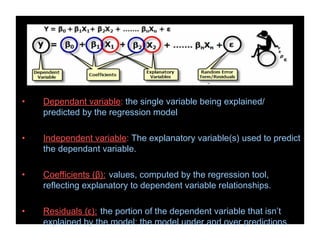
- Regression analysis is a statistical tool used to examine relationships between variables and can help predict future outcomes. It allows one to assess how the value of a dependent variable changes as the value of an independent variable is varied.
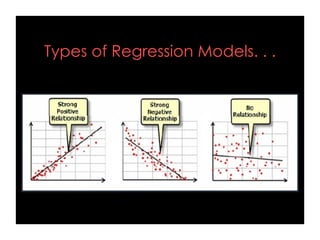
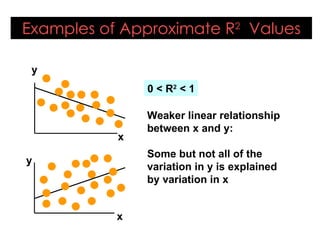
- Simple linear regression involves one independent variable, while multiple regression can include any number of independent variables. Regression analysis outputs include coefficients, residuals, and measures of fit like the R-squared value.
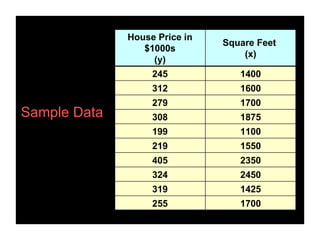
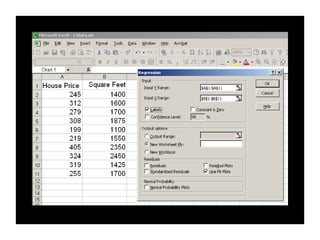
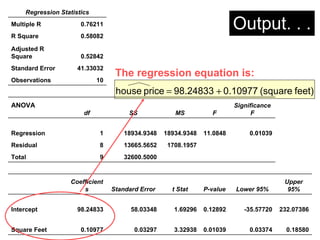
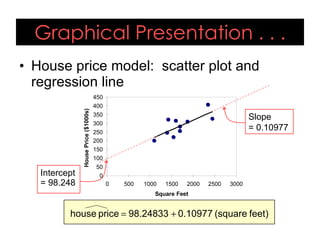
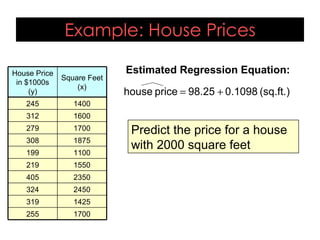
- An example uses home size and price data from 10 houses to generate a linear regression equation predicting that price increases by around $110 for each additional square foot. This model explains 58% of the variation in home prices.
![REGRESSION ANALYSIS M.Ravishankar [ And it’s application in Business ]](https://image.slidesharecdn.com/regressionanalysis-110723130213-phpapp02/75/Regression-analysis-1-2048.jpg)


















![M.RAVISHANKAR MBA(AB) 2008-2010 Batch NIFTTEA KNITWEAR FASHION INSTITUTE TIRUPUR [email_address]](https://image.slidesharecdn.com/regressionanalysis-110723130213-phpapp02/85/Regression-analysis-29-320.jpg)

