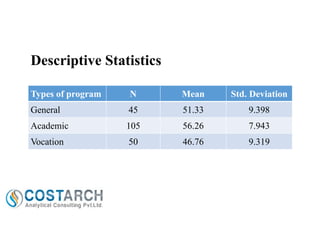
Logistic regression is a statistical method used to predict a binary or categorical dependent variable from continuous or categorical independent variables. It generates coefficients to predict the log odds of an outcome being present or absent. The method assumes a linear relationship between the log odds and independent variables. Multinomial logistic regression extends this to dependent variables with more than two categories. An example analyzes high school student program choices using writing scores and socioeconomic status as predictors. The model fits significantly better than an intercept-only model. Increases in writing score decrease the log odds of general versus academic programs.

1. Logistic Regression
Analysis
-By
PIE TUTORS
…your statistical partner…
www.pietutors.com

2. OUTLINE
• Introduction
• Assumptions
• Model development
• Example
• References

3. Introduction
• Logistic Regression is a statistical method for analyzing a dataset
in which there are one or more independent variables that
determine an outcome. The outcome is measured with a
dichotomous variable, where there are only two possible outcomes.
• The goal of logistic regression is to find the best fitting model to
describe the relationship between the dichotomous characteristic of
interest, and a set of independent variables.
• Logistic Regression generates the coefficients of a formula to
predict a Logit Transformation of the probability of presence of the
characteristic of interest.

4. Assumptions
• Assumes a linear relationship between the logit of the IVs and
DVs.
• Absence of multi-collinearity.
• Normal distribution is not assumed for the dependent variable as
well as for errors.
• Larger samples are needed than for linear regression.
• The dependent variable must be a dichotomy (2 categories).
• The independent variables need not be interval, nor normally
distributed, nor of equal variance within each group.

5. Model Development
1. Binary Logistic Regression
As Logistic Regression gives the formula to predict a logit
transformation of probability of presence of character of interest, so,
the model is,
+…….+
In logistic regression, the dependent variable is in fact a logit, which
is a log of odds,
1

6. So, the required probability is-

7. 2. Multinomial Logistic Regression
Multinomial logit regression is used when the dependent variable in
question is nominal and for which there are more than two
categories.
Two additional assumptions:1. The multinomial logit model assumes that data are case
specific, that is, each independent variable has a single value for
each case.
2. There is no need for the independent variables to be
statistically independent from each other.

8. Model:In multinomial logistic regression there are more than two
categories for dependent variable, so the probability of belonging to
category ‘j’ is given by-
=j)=
∑

9. Example
Description:- Entering high school students make program choices
among general program, vocational program and academic
program. Their choice might be modeled using their writing score
and their social economic status.
Description of the data:- The data set contains variables on 200
students. The outcome variable is prog, program type. The predictor
variables are social economic status, ses, a three-level categorical
variable and writing score, write, a continuous variable.

10. Descriptive Statistics
Types of program
N
Mean
Std. Deviation
General
45
51.33
9.398
Academic
105
56.26
7.943
Vocation
50
46.76
9.319

11. Now, by using multinomial logit modelFitting-criteria
Likelihood ratio test
model
-2 log likelihood Chi-square
Intercept only
206.756
Sig.
6
.000
254.986
Final
df
48.230

12. Results
• The Pseudo R- square value for the model is 0.21.
• The likelihood ratio chi-square of 48.23 with a p-value < 0.0001
tells us that our model as a whole fits significantly better than an
empty model. And the parameters are corresponding to two
equations:=
+
1 +
2 +
=
+
1 +
2 +

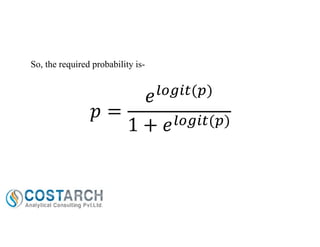
13. Parameters
Prog. type
Wald
df
Sig.
Intercept
1.689
1.896
1
.169
Write
‐.058
7.320
1
.007
.944
[ses=1]
1.163
5.114
1
.024
3.199
[ses=2]
.630
1.833
1
.176
1.877
[ses=3]
General
B
Exp(B)
0
0
Intercept
12.361
1
.000
Write
‐.114
26.139
1
.000
.893
[ses=1]
Vocation
4.236
.983
2.722
1
.099
2.672
[ses=2]
1.274
6.214
1
.013
3.575
[ses=3]
0
0

14. Interpretation
• A one-unit increase in the variable write is associated with a .058
decrease in the relative log odds of being in general program versus
academic program .
• A one-unit increase in the variable write is associated with a .1136
decrease in the relative log odds of being in vocation program
versus academic program.
• The relative log odds of being in general program versus in
academic program will increase by 1.163 if moving from the
highest level of ses (ses = 3) to the lowest level of ses (ses = 1).

15. References
1. http://www.schatz.sju.edu/multivar/guide/Logistic.pdf
2. http://www.ats.ucla.edu/stat/spss/dae/mlogit.htm