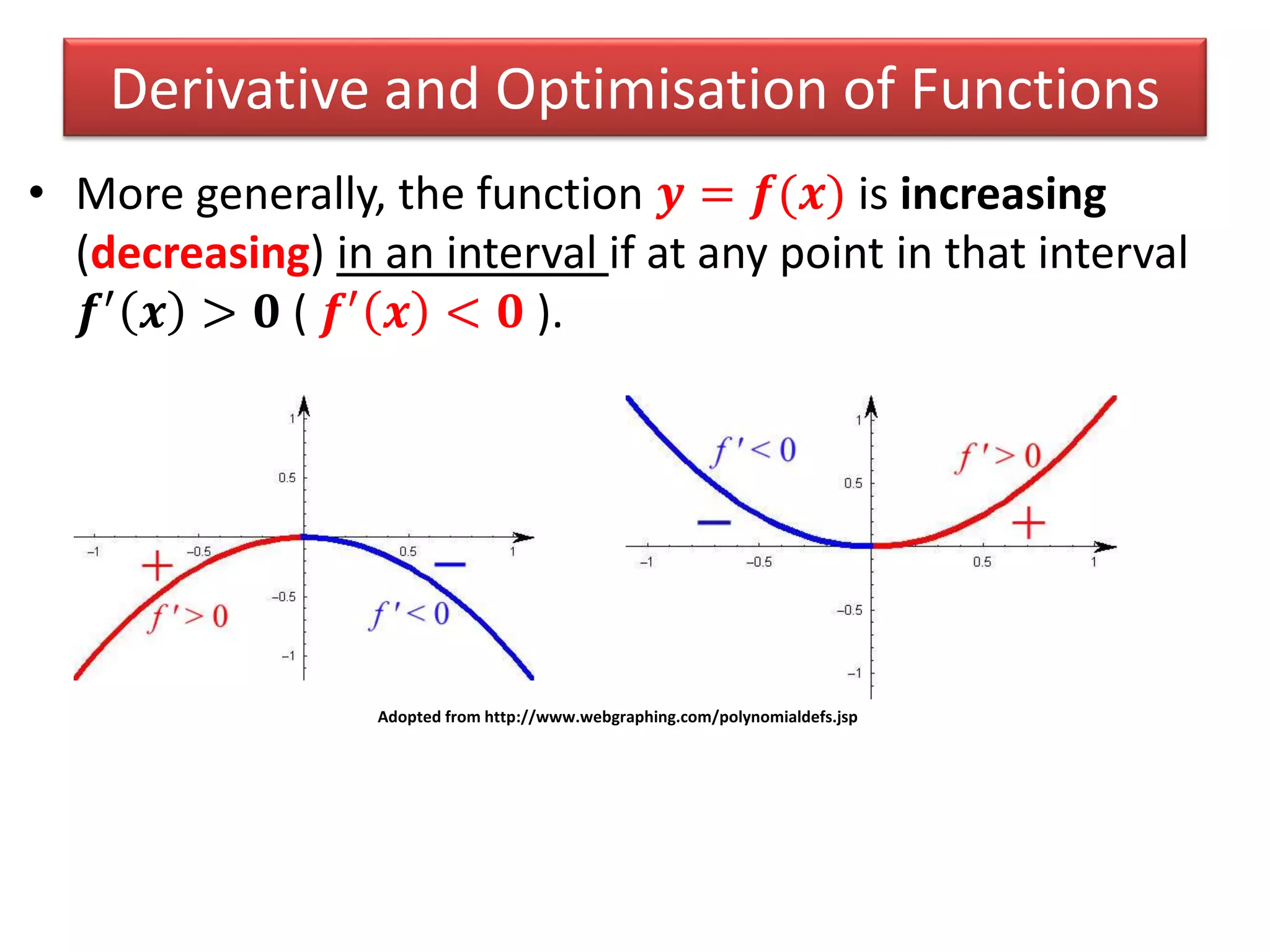
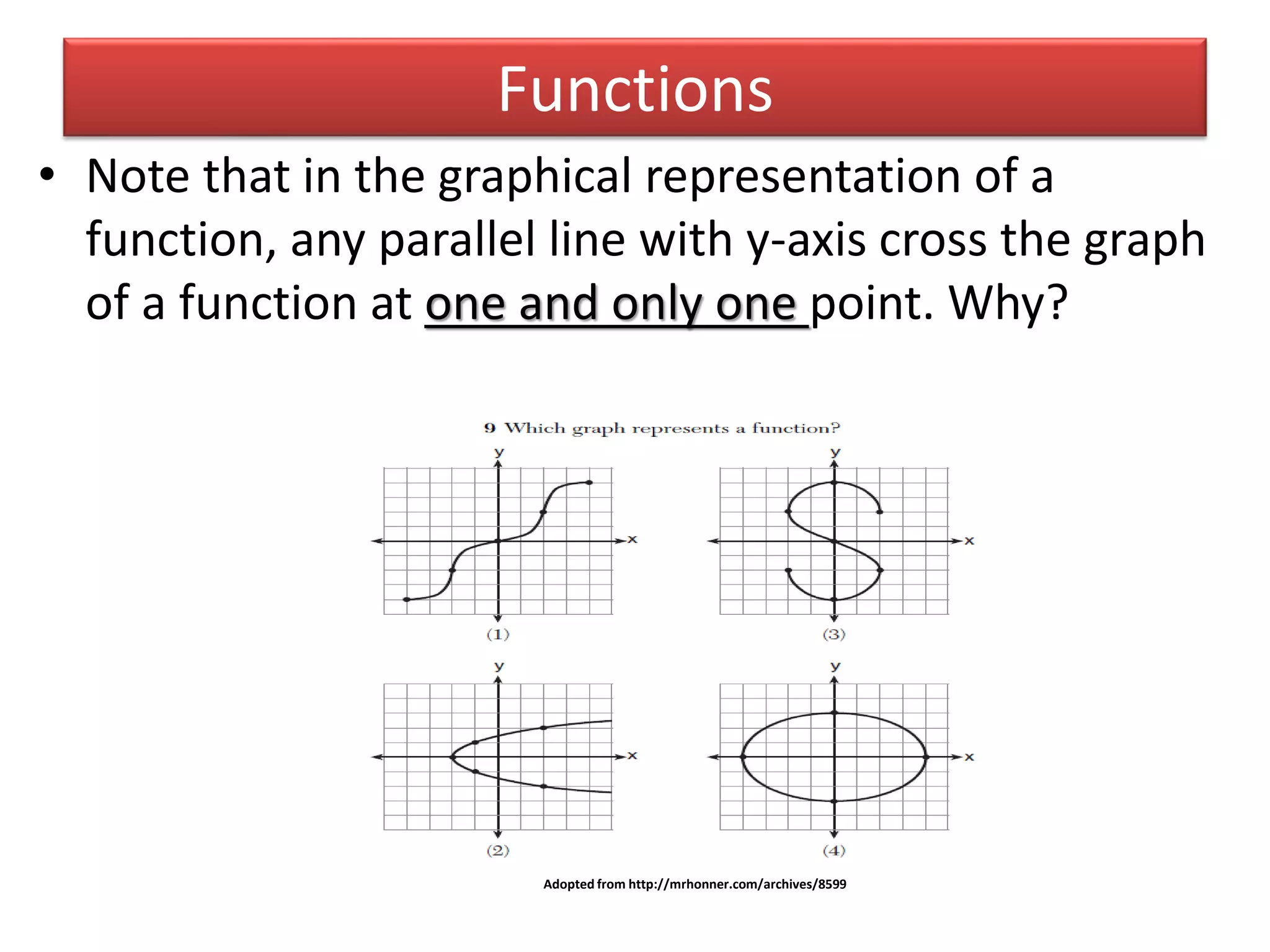
The document provides an overview of basic calculus concepts including: - Exponents and exponent rules for multiplying, dividing, and raising to powers. - Algebraic expressions including monomials, binomials, polynomials, and equations. - Common identities for exponents, polynomials, trigonometric functions. - The definition of a function as a correspondence between variables where each input has a single output. 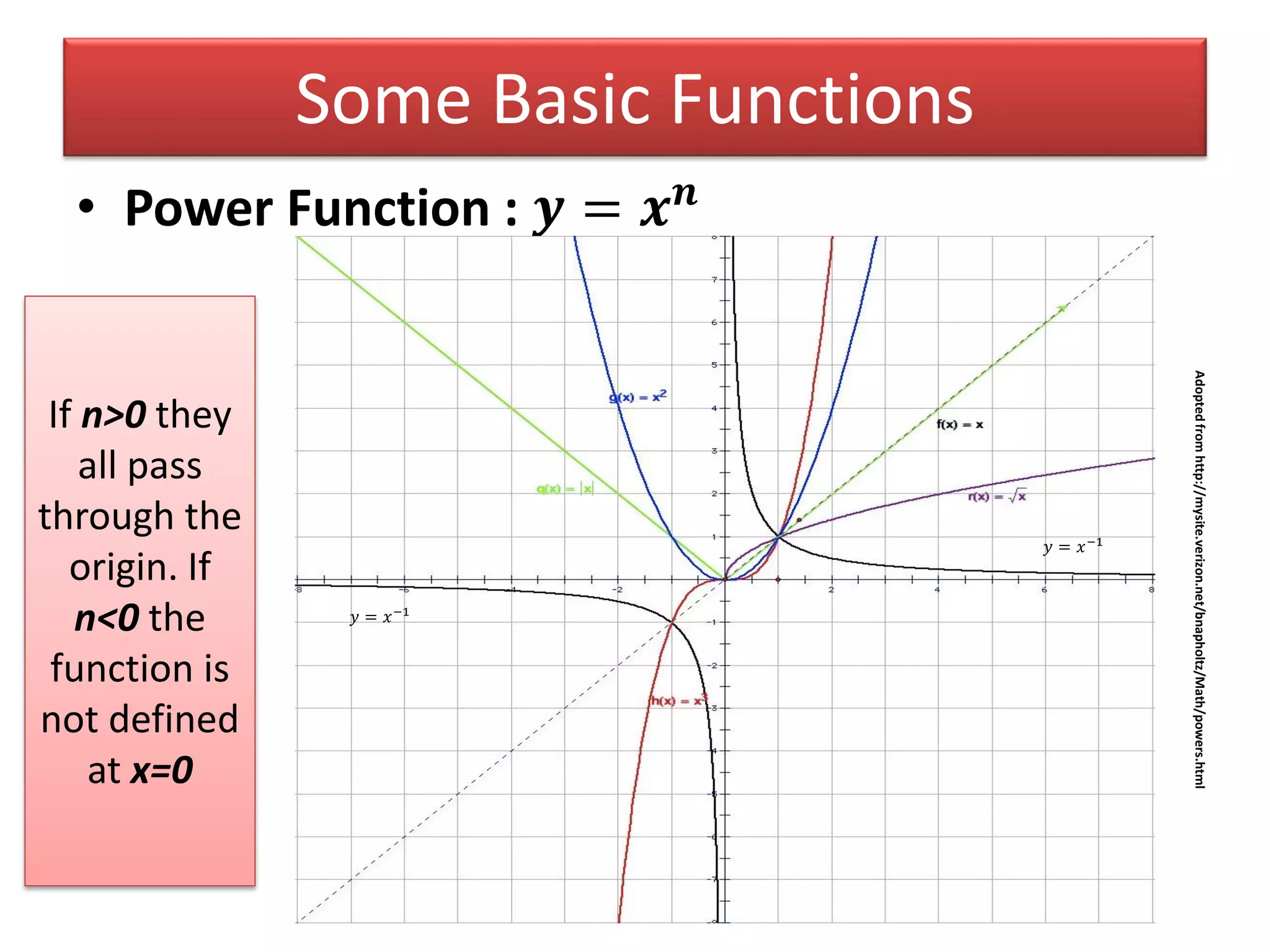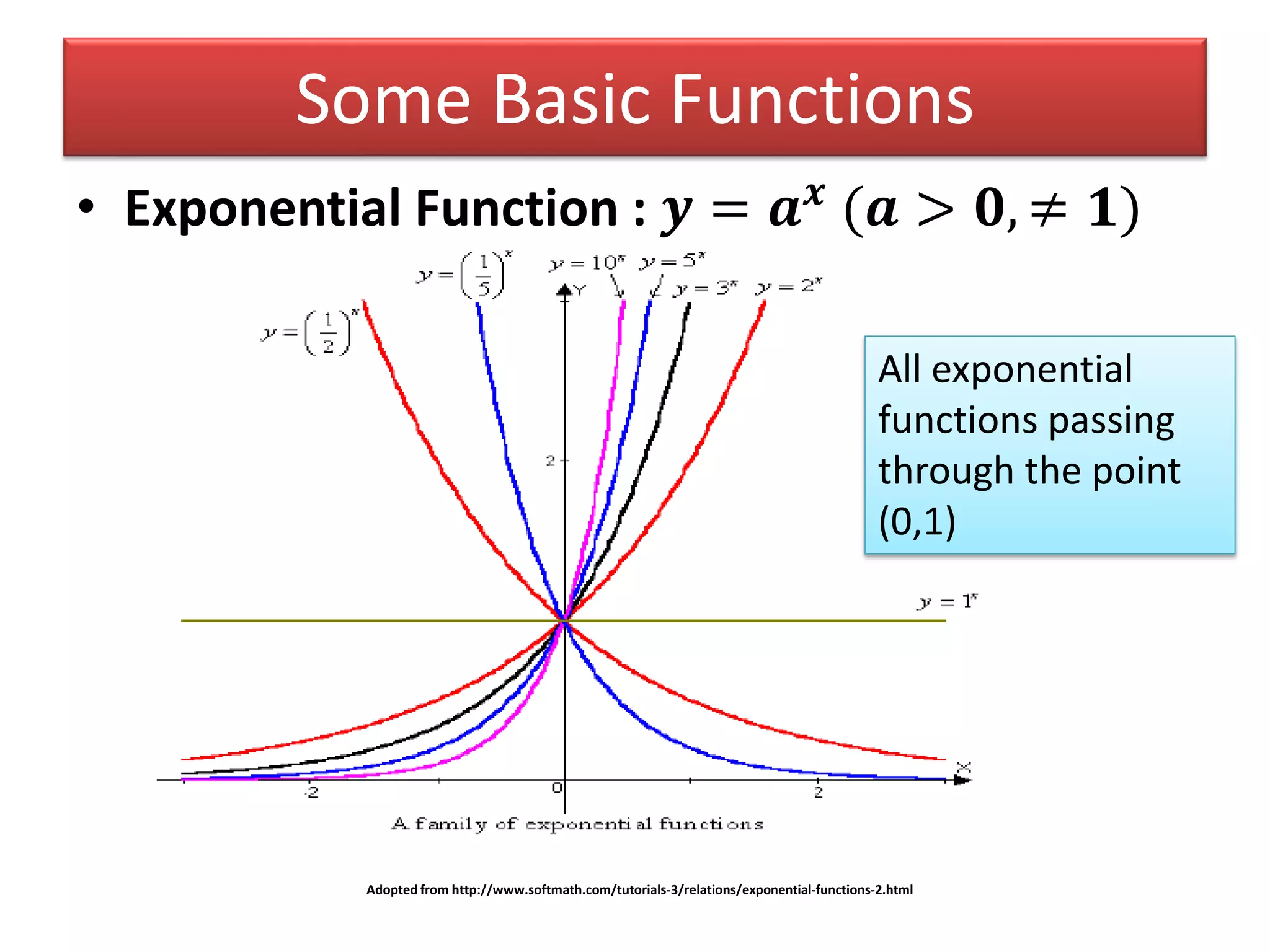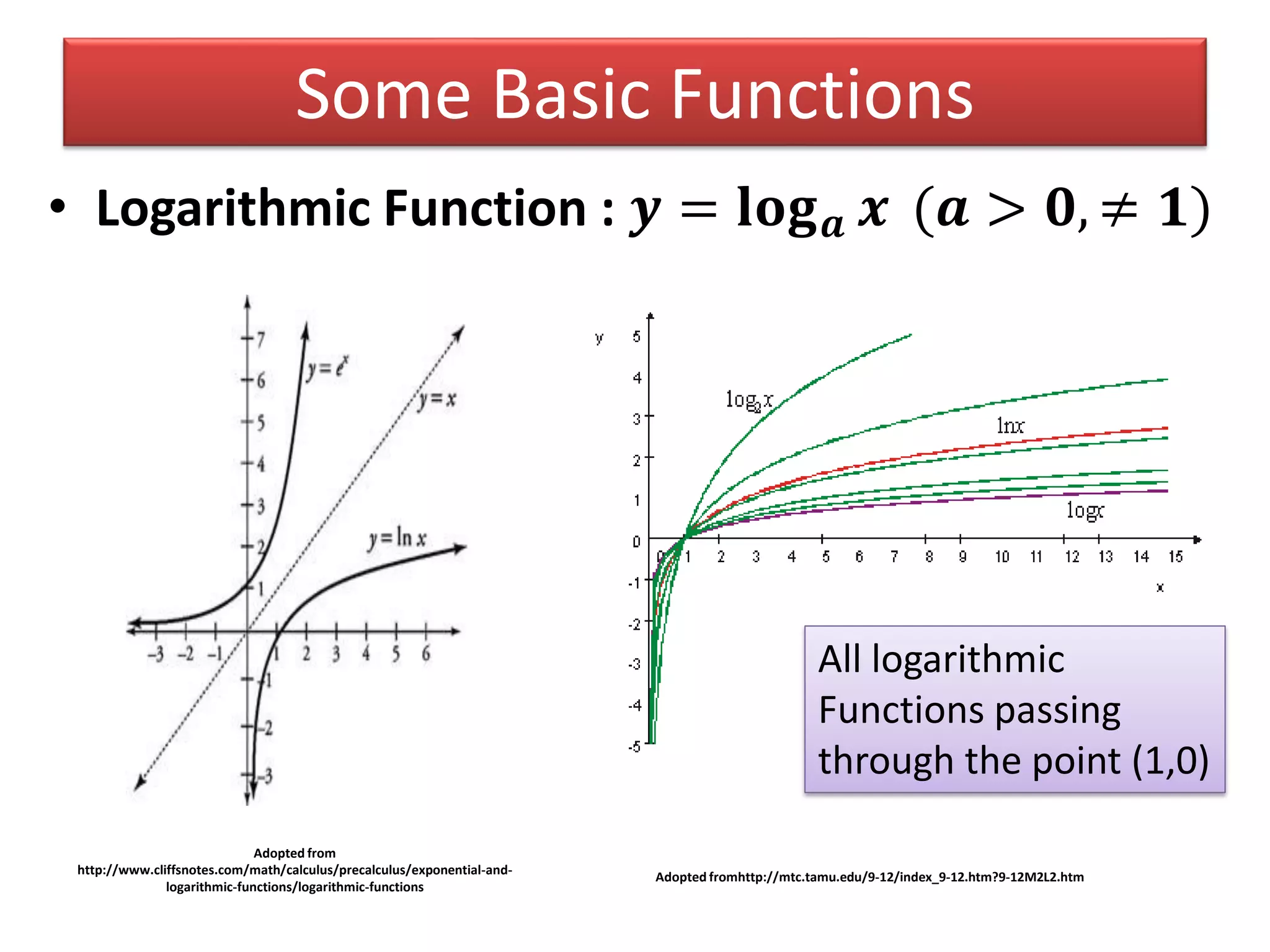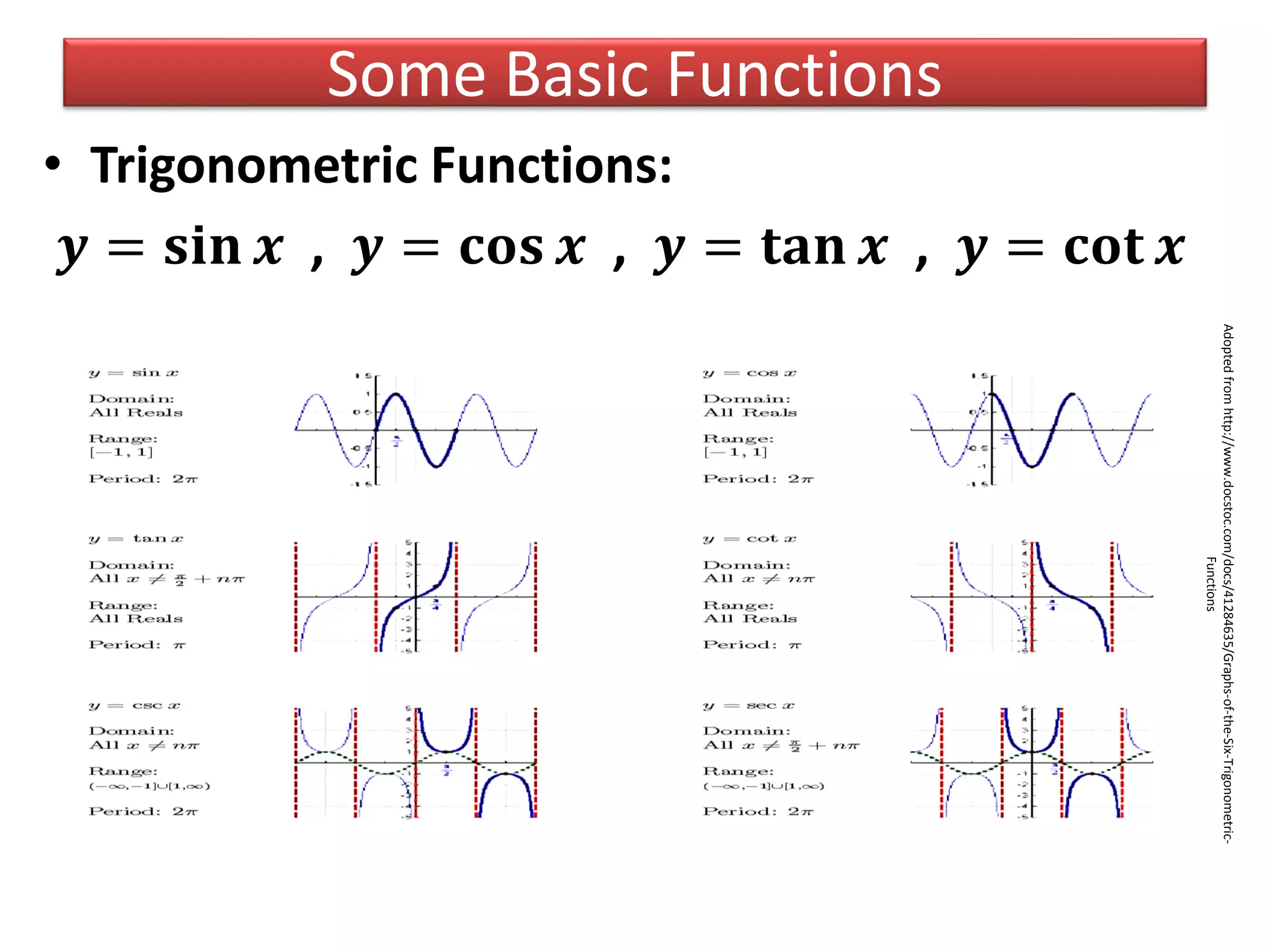- Examples of basic functions including power, exponential, logarithmic, and trigonometric functions.

1. Basic Calculus (I) Recap
(for MSc & PhD Business, Management & Finance Students)
First Draft: Autumn 2013
Revised: Autumn 2014
Lecturer: Farzad Javidanrad
One-Variable
Functions

2. Exponents (Powers)
• Given 𝒏 a positive integer and 𝒂 a real number,
𝒂 𝒏
indicates that 𝒂 is multiplied by itself 𝒏 times:
𝒂 𝒏
= 𝒂 × 𝒂 × ⋯ × 𝒂
𝒏 𝒕𝒊𝒎𝒆𝒔
• According to definition:
𝒂 𝟎
= 𝟏 and 𝒂 𝟏
= 𝒂

3. Exponents Rules
 If 𝒎 and 𝒏 are positive integers and 𝒂 is a real
number, then:
𝒂 𝒎
× 𝒂 𝒏
= 𝒂 𝒎+𝒏
With this rule we can define the concept of negative
exponent (power):
𝑎0
= 1
𝑎 𝑚−𝑚
= 1
𝑎 𝑚+(−𝑚)
= 1
𝑎 𝑚
× 𝑎−𝑚
= 1
𝒂−𝒎
=
𝟏
𝒂 𝒎

4. Exponents Rules
• We can also define rational power as:
𝒂
𝒎
𝒏 =
𝒏
𝒂 𝒎
Some other rules are: (𝒂 and 𝒃 are real numbers)

𝒂 𝒎
𝒂 𝒏 = 𝒂 𝒎−𝒏
e.g.(
311
38 = 311−8
= 33
= 27)
 𝒂 𝒎 𝒏
= 𝒂 𝒏 𝒎
= 𝒂 𝒎.𝒏
( 23 2 = 22 3 = 26 = 64)
 𝒂. 𝒃 𝒎
= 𝒂 𝒎
. 𝒃 𝒎
( 3. 𝑥 2 = 32. 𝑥2 = 9𝑥2)

𝒂
𝒃
𝒎
=
𝒂 𝒎
𝒃 𝒎 (
3
5
3
=
33
53 =
27
125
)
 𝒂
−𝒎
𝒏 =
𝟏
𝒂
𝒎
𝒏
=
𝟏
𝒏
𝒂 𝒎
=
𝟏
𝒏
𝒂
𝒎 (𝑥
−2
3 =
1
𝑥
2
3
=
1
3
𝑥2
)

5. Algebraic Expressions, Equations and Identities
• An algebraic expression is a combination of real numbers
and variables, such as:
Monomials :
5𝑥3
, −1.75
𝑦 ,
3𝑥
4𝑧2
=
3
4
𝑥𝑧−2
Binomials:
4𝑥3
+ 3𝑥2
,
3𝑥 + 1
4𝑧2
=
3
4
𝑥𝑧−2
+
1
4
𝑧−2
Polynomials:
𝑥2 − 3𝑥 − 6 , 𝑥3 + 𝑥𝑦2 + 6𝑥𝑦𝑧

6. Algebraic Expressions, Equations and Identities
• Equations can be made when two expressions are equal to
one another or an expression is equal to a number:
3𝑥 − 1 = 𝑥
4𝑥 + 3𝑦 = 2
5𝑥2 − 2𝑥𝑦 = 𝑥 − 6𝑦2
𝑥2 − 3𝑥 − 6 = 0
The first and second equations are linear with one and two
variables respectively and the third equation is a quadratic in
terms of 𝒙 and 𝒚 and the forth equation is a quadratic
equation in terms of 𝒙 .
Note: Not all equations are solvable and many of them have
no unique solutions.

7. Algebraic Expressions, Equations and Identities
• If two expressions are equal for all values of their
variable(s), the equation is called an identity.
• For example;
𝑥 + 3 2 = 𝑥2 + 6𝑥 + 9
 Some important identities are:
• 𝒂 ± 𝒃 𝟐 = 𝒂 𝟐 ± 𝟐𝒂𝒃 + 𝒃 𝟐
• 𝒂 ± 𝒃 𝟑
= 𝒂 𝟑
± 𝟑𝒂 𝟐
𝒃 + 𝟑𝒂𝒃 𝟐
± 𝒃 𝟑
• 𝒂 − 𝒃 𝒂 + 𝒃 = 𝒂 𝟐 − 𝒃 𝟐
• 𝒂 ± 𝒃 𝒂 𝟐
∓ 𝒂𝒃 + 𝒃 𝟐
= 𝒂 𝟑
± 𝒃 𝟑
• 𝒙 ± 𝒂 𝒙 ± 𝒃 = 𝒙 𝟐 ± 𝒂 + 𝒃 𝒙 + 𝒂𝒃

8. Some Other Identities
• 𝒙 − 𝒚 = 𝒙 − 𝒚 𝒙 + 𝒚
= 𝟑
𝒙 − 𝟑
𝒚
𝟑
𝒙 𝟐 + 𝟑
𝒙𝒚 +
𝟑
𝒚 𝟐
⋮
= 𝒏
𝒙 − 𝒏
𝒚
𝒏
𝒙 𝒏−𝟏 +
𝒏
𝒙 𝒏−𝟐 𝒚 +
𝒏
𝒙 𝒏−𝟑 𝒚 𝟐 + ⋯ +
𝒏
𝒚 𝒏−𝟏
• 𝒙 + 𝒚 + 𝒛 𝟐 = 𝒙 𝟐 + 𝒚 𝟐 + 𝒛 𝟐 + 𝟐𝒙𝒚 + 𝟐𝒙𝒛 + 𝟐𝒚𝒛
• 𝑠𝑖𝑛2
𝑥 + 𝑐𝑜𝑠2
𝑥 = 1
• 𝑠𝑖𝑛 𝑥 ± 𝑦 = 𝑠𝑖𝑛𝑥. 𝑐𝑜𝑠𝑦 ± 𝑐𝑜𝑠𝑥. 𝑠𝑖𝑛𝑦
• 𝑐𝑜𝑠 𝑥 ± 𝑦 = 𝑐𝑜𝑠𝑥. 𝑐𝑜𝑠𝑦 ∓ 𝑠𝑖𝑛𝑥. 𝑠𝑖𝑛𝑦
• 𝑡𝑎𝑛 𝑥 ± 𝑦 =
𝑡𝑎𝑛𝑥±𝑡𝑎𝑛𝑦
1∓𝑡𝑎𝑛𝑥.𝑡𝑎𝑛𝑦

9. • 𝒙 + 𝒚 𝒏 =
𝟎
𝒏
𝒙 𝒏 +
𝟏
𝒏
𝒙 𝒏−𝟏 𝒚 + ⋯ +
𝒓
𝒏
𝒙 𝒏−𝒓 𝒚 𝒓 + ⋯ +
𝒏
𝒏
𝒚 𝒏
Where
𝒓
𝒏
= 𝑪
𝒓
𝒏
= 𝒓𝑪 𝒏 =
𝒏!
𝒓! 𝒏 − 𝒓 !
And
𝒏! = 𝒏 × 𝒏 − 𝟏 × 𝒏 − 𝟐 × ⋯ × 𝟑 × 𝟐 × 𝟏
𝟎! = 𝟏! = 𝟏
So,
𝟎
𝒏
= 𝐶
0
𝑛
= 0𝐶 𝑛 =
𝑛!
0! 𝑛 − 0 !
=
𝑛!
𝑛!
= 𝟏
𝟏
𝒏
= 𝐶
1
𝑛
= 1𝐶 𝑛 =
𝑛!
1! 𝑛 − 1 !
=
𝑛!
𝑛 − 1 !
=
𝑛 × 𝑛 − 1 !
𝑛 − 1 !
= 𝒏
𝟐
𝒏
= 𝐶
2
𝑛
= 2𝐶 𝑛 =
𝑛!
2! 𝑛 − 2 !
=
𝑛!
𝑛 − 2 !
=
𝑛 × 𝑛 − 1 × 𝑛 − 2 !
2! 𝑛 − 2 !
=
𝒏(𝒏 − 𝟏)
𝟐
Some Other Identities

10. Functions
• All equations represent a relationship between two or
more variables, e.g.:
𝑥𝑦 = 1 ,
𝑥
2𝑦
+ 𝑧 = 0
• Given two variables in relation, there is a functional
relationship between them if for each value of one of
them there is one and only one value of another.
• If the relationship between 𝒚 and 𝒙 can be shown by 𝒚 =
𝒇 𝒙 and for each value of 𝒙 there is one and only one
value of 𝒚 , then there is a functional relationship
between them or alternatively it can be said that 𝒚 is a
function of 𝒙 , which means 𝒚 as a dependent variable
follows 𝒙 as an independent variable.

11. Functions
• The idea of function is close to a processing (matching)
machine. It receives inputs (which are the values of 𝒙 and is
called domain of the function, 𝑫 𝒇) and after the processing
them the output will be values of 𝒚 in correspondence with
𝒙′
𝒔 (which is called range of the function, 𝑹 𝒇).
• There should be no element from 𝑫 𝒇 without a match from
𝑹 𝒇, but it might be found some free elements in 𝑹 𝒇.
𝒇 = 𝒙 𝟏, 𝒚 𝟏 , 𝒙 𝟐, 𝒚 𝟐 , … , 𝒙 𝒏, 𝒚 𝒏
𝒇
𝒙 𝟏, 𝒙 𝟐, … , 𝒙 𝒏 𝒚 𝟏, 𝒚 𝟐, … , 𝒚 𝒏

12. Functions
• Functions can be considered as correspondence
(matching) rules, which corresponds all elements of
𝒙 to some elements of 𝒚.*
• For example, the correspondence rule (f), which
corresponds 𝒙 to each value of 𝒙, can be written
as:
Or 𝑦 = 𝑥
xxf : 1
2
4
15
1
𝟐
2
𝟏𝟓
20
x y

13. Functions
• The correspondence rule, which corresponds
𝒙 𝟐
− 𝟏𝟎 to each value of 𝒙 can be shown as:
Or 𝒚 = 𝒙 𝟐
− 𝟏𝟎
10: 2
xxg 
-3
-2
0
2
3
-1
-6
-10
x y

14. Functions
• Some correspondence rules indicate there is a relationship
between 𝒙 and 𝒚 but not a functional relationship, i.e.
the relationship cannot be considered as a function.
• For example, 𝒚 = ± 𝒙 (𝒚 𝟐 = 𝒙) is
not a function (according to the
definition of function) because
for each value of 𝒙 there are
two symmetrical values of 𝒚 .
Adopted from http://www.education.com/study-help/article/trigonometry-help-inverses-circular/

15. Functions
• Note that in the graphical representation of a
function, any parallel line with y-axis cross the graph
of a function at one and only one point. Why?
Adopted from http://mrhonner.com/archives/8599

16. Some Basic Functions
• Power Function : 𝒚 = 𝒙 𝒏
Adoptedfromhttp://mysite.verizon.net/bnapholtz/Math/powers.html
If n>0 they
all pass
through the
origin. If
n<0 the
function is
not defined
at x=0
𝑦 = 𝑥−1
𝑦 = 𝑥−1

17. Some Basic Functions
• Exponential Function : 𝒚 = 𝒂 𝒙
(𝒂 > 𝟎, ≠ 𝟏)
Adopted from http://www.softmath.com/tutorials-3/relations/exponential-functions-2.html
All exponential
functions passing
through the point
(0,1)

18. Some Basic Functions
• Logarithmic Function : 𝒚 = 𝐥𝐨𝐠 𝒂 𝒙 (𝒂 > 𝟎, ≠ 𝟏)
Adopted fromhttp://mtc.tamu.edu/9-12/index_9-12.htm?9-12M2L2.htm
Adopted from
http://www.cliffsnotes.com/math/calculus/precalculus/exponential-and-
logarithmic-functions/logarithmic-functions
All logarithmic
Functions passing
through the point (1,0)

19. Some Basic Functions
• Trigonometric Functions:
𝒚 = 𝐬𝐢𝐧 𝒙 , 𝒚 = 𝐜𝐨𝐬 𝒙 , 𝒚 = 𝐭𝐚𝐧 𝒙 , 𝒚 = 𝐜𝐨𝐭 𝒙
Adoptedfromhttp://www.docstoc.com/docs/41284635/Graphs-of-the-Six-Trigonometric-
Functions

20. • All trigonometric functions are periodic, i.e. after adding or
subtracting a constant, which is called principal periodic constant,
they repeat themselves. This periodic constant is 𝟐𝝅 for 𝒔𝒊𝒏𝒙
and 𝒄𝒐𝒔𝒙 but it is 𝝅 for 𝒕𝒂𝒏𝒙 and 𝒄𝒐𝒕𝒙 , i.e. :
(k is a positive integer)
𝑠𝑖𝑛𝑥 = sin 𝑥 ± 𝟐𝝅 = sin 𝑥 ± 4𝜋 = ⋯ = sin 𝑥 ± 2𝑘𝜋
𝑐𝑜𝑠𝑥 = cos 𝑥 ± 𝟐𝝅 = cos 𝑥 ± 4𝜋 = ⋯ = cos 𝑥 ± 2𝑘𝜋
𝑡𝑎𝑛𝑥 = tan 𝑥 ± 𝝅 = tan 𝑥 ± 2𝜋 = ⋯ = tan(𝑥 ± 𝑘𝜋)
𝑐𝑜𝑡𝑥 = cot 𝑥 ± 𝝅 = cot 𝑥 ± 2𝜋 = ⋯ = cot(𝑥 ± 𝑘𝜋)
Some Basic Functions

21. Elementary Functions
• Elementary functions can be made by combining
basic functions through adding, subtracting,
multiplying, dividing and also composing these
basic functions.
• For example:
𝑦 = 𝑥2
+ 4𝑥 − 1
𝑦 = 𝑥. 𝑒−𝑥
=
𝑥
𝑒 𝑥
𝑦 = 𝑒 𝑠𝑖𝑛𝑥
𝑦 = ln 𝑥2 + 4
𝑦 = 𝑒 𝑥
(𝑠𝑖𝑛3𝑥 − 𝑐𝑜𝑠3𝑥)

22. Behaviour of a Function
• After finding the relationship between two variables 𝒙
and 𝒚 in the functional form 𝒚 = 𝒇(𝒙) the first question is
how this function behaves.
• Here we are interested in knowing about the magnitude
and the direction of the change of 𝒚 (𝑖. 𝑒. ∆𝒚) when the
change of 𝒙 (𝑖. 𝑒. ∆𝒙) is getting smaller and smaller around
a point in its domain. The technical term for this locality
around a point is neighbourhood. So, we are trying to find
the magnitude and the direction of the change of 𝒚 in the
neighbourhood of 𝒙.
• Slope of a function is the concept which helps us to have
this information. The value of the slope shows the
magnitude of the change and the sign of slope shows the
direction of the change.

23. Slope of a Linear Function
• Let’s start with one of the most used functions in
science , which is the linear function:
𝒚 = 𝒎𝒙 + 𝒉
Where 𝒎 shows the slope of the line (the average change
of 𝒚 in terms of a change in 𝒙). That is; 𝒎 =
𝚫𝒚
𝚫𝒙
= 𝐭𝐚𝐧 𝜶 .
The value of intercept is 𝒉 which is the distance between the
intersection point of the graph and y-axis from the Origin.
The slope of a liner
function is constant in its
whole domain.
y
x
h
𝒚 = 𝒎𝒙 + 𝒉
∆𝒙
∆𝒚
𝜶
𝜶

24. Slope of a Function in its General Form
• Imagine we want to find the slope of the function 𝒚 = 𝒇(𝒙)
at a specific point (for e.g. at 𝒙 𝟎) in its domain.
• Given a change of
𝒙 from 𝒙 𝟎 to 𝒙 𝟎 + ∆𝒙
the change of 𝒚
Would be from 𝒇 𝒙 𝟎
to 𝒇(𝒙 𝟎 + ∆𝒙) .
• This means a
movement along the
curve from A to B. Adopted from http://www.bymath.com/studyguide/ana/sec/ana3.htm

25. Slope of a Function in its General Form
• The average change of 𝒚 in terms of a change in 𝒙
can be calculated by
𝚫𝒚
𝚫𝒙
= 𝐭𝐚𝐧 𝜶 , which is the
slope of the line AB.
• If the change in 𝒙 gradually disappear (∆𝒙 → 𝟎)*,
point B moves toward point A and the slope line
(secant line) AB reaches to a limiting (marginal)
situation AC, which is a tangent line on the curve
of 𝒚 = 𝒇(𝒙) at point 𝑨(𝒙 𝟎, 𝒇(𝒙 𝟎)).

26. Slope of a Function in its General Form
• The slope of this tangent line AC is what is called derivative
of 𝒚 in terms of 𝒙 at point 𝑥0 and it is shown by different
symbols such as
𝑑𝑦
𝑑𝑥 𝑥=𝑥0
, 𝑓′
𝑥0 ,
𝑑𝑓
𝑑𝑥 𝑥=𝑥0
, 𝑦′
(𝑥0) , .
• The slope of the tangent line at any point of the domain of
the function is denoted by:
𝑑𝑦
𝑑𝑥
, 𝑓′ 𝑥 ,
𝑑𝑓
𝑑𝑥
, 𝑦′, 𝑓𝑥
′
• Definition: The process of finding a derivative of a function
is called differentiation .
'
0xf

27. Slope of a Function in its General Form
• Therefore, the derivative of 𝒚 = 𝒇(𝒙)at any point in its
domain is:
𝒚′ =
𝒅𝒚
𝒅𝒙
= 𝒍𝒊𝒎
∆𝒙→𝟎
∆𝒚
∆𝒙
= 𝒍𝒊𝒎
∆𝒙→𝟎
𝒇 𝒙+∆𝒙 −𝒇(𝒙)
∆𝒙
And the derivative of 𝒚 = 𝒇(𝒙) at the specific point 𝒙 = 𝒙 𝟎
is:
𝒇′ 𝒙 𝟎 = 𝐥𝐢𝐦
∆𝒙→𝟎
𝒇 𝒙 𝟎 + ∆𝒙 − 𝒇(𝒙 𝟎)
∆𝒙
Where 𝐥𝐢𝐦 stands for “limit”, showing limiting (marginal)
situation of the ratio
𝚫𝒚
𝚫𝒙
.

28. Slope of a Function in its General Form
• Note: For non-linear functions, slope of the function at
any point depends on the value of that point and it is not
constant in the whole domain of the function. This
means that the derivative of a function is a function of
the same variable itself.
Adopted from http://www.columbia.edu/itc/sipa/math/slope_nonlinear.html
http://www.pleacher.com/mp/mlessons/calc2006/day21.html

29. Derivative of Fundamental Basic Functions
• Find the derivative of 𝑦 = 2𝑥 − 1 at any point in
its domain.
𝑓 𝑥 = 2𝑥 − 1
𝑓 𝑥 + ∆𝑥 = 2 𝑥 + ∆𝑥 − 1 = 2𝑥 + 2∆𝑥 − 1
∆𝒚 = 𝒇 𝒙 + ∆𝒙 − 𝒇 𝒙 = 𝟐∆𝒙
According to definition:
𝑦′ =
𝑑𝑦
𝑑𝑥
= lim
∆𝑥→0
𝑓 𝑥 + ∆𝑥 − 𝑓(𝑥)
∆𝑥
= lim
∆𝑥→0
2∆𝑥
∆𝑥
= 2

30. Derivative of the Fundamental Basic Functions
• Applying the same method, the derivative of the
fundamental basic functions can be obtained as
following:
 𝒚 = 𝒙 𝒏
→ 𝒚′
= 𝒏𝒙 𝒏−𝟏
e.g. :
𝑦 = 3 → 𝑦′ = 0
𝑦 = 𝑥3 → 𝑦′ = 3𝑥2
𝑦 = 𝑥−1 → 𝑦′ = −𝑥−2
𝑦 = 5
𝑥 → 𝑦′
=
1
5
𝑥
1
5
−1
=
1
5
5
𝑥4

31. Derivative of the Fundamental Basic Functions
 𝒚 = 𝒂 𝒙 → 𝒚′ = 𝒂 𝒙. 𝒍𝒏𝒂 𝑎 > 0, ≠ 1
e.g. :
𝑦 = 2 𝑥 → 𝑦′ = 2 𝑥. 𝑙𝑛2
𝑦 = 𝑒 𝑥 → 𝑦′ = 𝑒 𝑥
 𝒚 = 𝐥𝐨𝐠 𝒂 𝒙 → 𝒚′
=
𝟏
𝒙.𝒍𝒏𝒂
e.g. :
𝑦 = log 𝑥 → 𝑦′ =
1
𝑥. 𝑙𝑛10
𝑦 = ln 𝑥 → 𝑦′ =
1
𝑥

32. Derivative of the Fundamental Basic Functions
 𝒚 = 𝐬𝐢𝐧 𝒙 → 𝒚′
= 𝐜𝐨𝐬 𝒙
 𝒚 = 𝐜𝐨𝐬 𝒙 → 𝒚′
= − 𝐬𝐢𝐧 𝒙
 𝒚 = 𝐭𝐚𝐧 𝒙 → 𝒚′
= 𝟏 + 𝐭𝐚𝐧 𝟐
𝐱 =
𝟏
𝐜𝐨𝐬 𝟐 𝐱
 𝒚 = 𝐜𝐨𝐭 𝒙 → 𝒚′
= − 𝟏 + 𝐜𝐨𝐭 𝟐
𝐱 =
−𝟏
𝐬𝐢𝐧 𝟐 𝐱

33. Differentiability of a Function
A function is differentiable at a point if despite any
side approach to the point in its domain (from left or
right) the derivative is the same and a finite number.
Sharp corner points and points of discontinuity* are
not differentiable.
Adopted from Ahttp://www-math.mit.edu/~djk/calculus_beginners/chapter09/section02.html

34. Rules of Differentiation
• If 𝒇(𝒙) and 𝒈 𝒙 are two differentiable functions in their
common domain, then:
 𝒇(𝒙) ± 𝒈(𝒙) ′ = 𝒇′(𝒙) ± 𝒈′(𝒙)
 𝒇 𝒙 . 𝒈(𝒙) ′ = 𝒇′ 𝒙 . 𝒈 𝒙 + 𝒈′ 𝒙 . 𝒇(𝒙)

𝒇(𝒙)
𝒈(𝒙)
′
=
𝒇′ 𝒙 .𝒈 𝒙 −𝒈′ 𝒙 .𝒇(𝒙)
𝒈(𝒙) 𝟐 (Quotient Rule)
 𝒇(𝒈 𝒙 ) ′ = 𝒈′ 𝒙 . 𝒇′(𝒈 𝒙 ) (Chain Rule)
(Summation & Sub. Rules. They
can be extended to n functions)
(Multiplication Rule
and can be extended
to n functions)

35.  Find the derivative of the following functions:
o 𝑦 = 𝑥 + 𝑙𝑛𝑥 ∶ 𝒚′ = 𝟏 +
𝟏
𝒙
o 𝑦 = 𝑒 𝑥. 𝑠𝑖𝑛𝑥 ∶ 𝒚′ = 𝒆 𝒙. 𝒔𝒊𝒏𝒙 + 𝒆 𝒙. 𝒄𝒐𝒔𝒙
= 𝒆 𝒙 𝒔𝒊𝒏𝒙 + 𝒄𝒐𝒔𝒙
o 𝑦 =
2𝑥
𝑥2+1
∶ 𝒚′ =
𝟐 𝒙 𝟐+𝟏 −𝟐𝒙.𝟐𝒙
𝒙 𝟐+𝟏
𝟐 =
𝟏−𝟐𝒙 𝟐
𝒙 𝟐+𝟏
𝟐
o 𝑦 =
3
𝑥2 + 1 ∶ 𝒚′ = 𝟐𝒙.
𝟏
𝟑
. 𝒙 𝟐 + 𝟏
𝟏
𝟑
−𝟏
=
𝟐𝒙
𝟑
𝟑
𝒙 𝟐+𝟏
𝟐
Rules of Differentiation

36. o 𝑦 = 𝑙𝑛2 𝑥 ∶ 𝒚′ =
𝟏
𝒙
. 𝟐. 𝒍𝒏𝒙 =
𝟐𝒍𝒏𝒙
𝒙
o 𝑦 = 5 𝑥2
+ tan 3𝑥 ∶ 𝒚′ = 𝟓 𝒙 𝟐
. 𝐥𝐧𝟓. (𝟐𝒙) + 𝟑(𝟏 + 𝒕𝒂𝒏 𝟐 𝟑𝒙)
• The last rule(page 32) is called the chain rule which should
be applied for composite functions such as the above
functions, but it can be extended to include more
functions.
• If 𝒚 = 𝒇 𝒖 and 𝒖 = 𝒈 𝒛 and 𝒛 = 𝒉 𝒍 and 𝒍 = 𝒌(𝒙)
then 𝒚 depends on 𝒙 but through some other variables
𝒚 = 𝒇 𝒈 𝒉 𝒌 𝒙
Rules of Differentiation

37. • Under such circumstances we can extend the chain rule
to cover all these functions, i.e.
𝒅𝒚
𝒅𝒙
=
𝒅𝒚
𝒅𝒖
.
𝒅𝒖
𝒅𝒛
.
𝒅𝒛
𝒅𝒍
.
𝒅𝒍
𝒅𝒙
o 𝑦 = 𝑐𝑜𝑠3
2𝑥 + 1 ∶
𝑦 = 𝑢3
𝑢 = 𝑐𝑜𝑠𝑧
𝑧 = 2𝑥 + 1
𝒚′ =
𝒅𝒚
𝒅𝒙
=
𝒅𝒚
𝒅𝒖
.
𝒅𝒖
𝒅𝒛
.
𝒅𝒛
𝒅𝒙
= 𝟑𝒖 𝟐. −𝒔𝒊𝒏𝒛 . 𝟐
= −𝟔𝒄𝒐𝒔 𝟐 𝟐𝒙 + 𝟏 . 𝐬𝐢𝐧(𝟐𝒙 + 𝟏)
Rules of Differentiation

38. Implicit Differentiation
• 𝒚 = 𝒇 𝒙 is an explicit function because the dependent
variable 𝒚 is at one side and explicitly expressed by
independent variable 𝒙. Implicit form of this function can
be shown by 𝑭 𝒙, 𝒚 = 𝟎 where both variables are in one
side:
o Explicit Functions: 𝑦 = 𝑥2 − 3𝑥 , 𝑦 = 𝑒 𝑥. 𝑙𝑛𝑥 , 𝑦 =
𝑠𝑖𝑛𝑥
𝑥
o Implicit Functions: 2𝑥 − 7𝑦 + 3 = 0 , 2 𝑥𝑦 − 𝑦2 = 0
• Many implicit functions can be easily transformed to an
explicit function but it cannot be done for all. In this case,
differentiation with respect to 𝒙 can be done part by part
and 𝒚 should be treated as a function of 𝒙.

39. o Find the derivative of 𝟐𝒙 − 𝟕𝒚 + 𝟑 = 𝟎.
Differentiating both sides with respect to 𝒙, we have:
𝑑
𝑑𝑥
2𝑥 − 7𝑦 + 3 =
𝑑
𝑑𝑥
0
2 − 7𝑦′ + 0 = 0 → 𝒚′ =
𝟐
𝟕
o Find the derivative of 𝒙 𝟐 − 𝟐𝒙𝒚 + 𝒚 𝟑 = 𝟎.
Using the same method, we have:
2𝑥 − 2𝑦 − 2𝑥𝑦′ + 3𝑦2 𝑦′ = 0 → 𝒚′ =
𝟐𝒚 − 𝟐𝒙
𝟑𝒚 𝟐 − 𝟐𝒙
Implicit Differentiation

40. o Find the derivative of 𝟐 𝒙𝒚 − 𝒚 𝟐 = 𝟎
𝑦 + 𝑥𝑦′ 2 𝑥𝑦 − 2𝑦𝑦′ = 0 → 𝒚′ =
𝒚. 𝟐 𝒙𝒚
𝟐𝒚 − 𝒙. 𝟐 𝒙𝒚
o Find the derivative of 𝒔𝒊𝒏
𝒙
𝒚
− 𝐥𝐧 𝒙𝒚 = 𝟎
𝑦 − 𝑥𝑦′
𝑦2
. 𝑐𝑜𝑠
𝑥
𝑦
−
𝑦 + 𝑥𝑦′
𝑥𝑦
= 0
Then
𝒚′
=
𝟏
𝒚
. 𝒄𝒐𝒔
𝒙
𝒚
−
𝟏
𝒙
𝒙
𝒚 𝟐 . 𝒄𝒐𝒔
𝒙
𝒚
+
𝟏
𝒚
Implicit Differentiation

41. Higher Orders Derivatives
• As 𝒚′ = 𝒇′(𝒙) is itself a function of 𝒙 , in case it is differentiable,
we can think of second, third or even n-th derivatives:
• Second Derivative:
𝒚′′
,
𝒅 𝟐 𝒚
𝒅𝒙 𝟐
,
𝒅(
𝒅𝒚
𝒅𝒙
)
𝒅𝒙
,
𝒅
𝒅𝒙
𝒇′
, 𝒇′′
𝒙
• Third Derivative:
𝒚′′′ ,
𝒅 𝟑
𝒚
𝒅𝒙 𝟑
,
𝒅(
𝒅 𝟐 𝒚
𝒅𝒙 𝟐)
𝒅𝒙
,
𝒅
𝒅𝒙
𝒇′′ , 𝒇′′′ 𝒙
• N-th Derivative:
𝒚(𝒏) ,
𝒅 𝒏 𝒚
𝒅𝒙 𝒏
,
𝒅(
𝒅(𝒏−𝟏)
𝒚
𝒅𝒙(𝒏−𝟏))
𝒅𝒙
,
𝒅
𝒅𝒙
𝒇(𝒏−𝟏) , 𝒇(𝒏) 𝒙

42. o Find the second and third derivatives of 𝒚 = 𝒆−𝒙.
𝑦′ = −𝑒−𝑥
𝑦′′ = 𝑒−𝑥
𝑦′′′ = −𝑒−𝑥
o If 𝒚 = 𝒆 𝜽𝒙
show that the equation 𝒚′′′
− 𝒚′′
= 𝟎 has
two roots.
𝑦′ = 𝜃𝑒 𝜃𝑥
𝑦′′
= 𝜃2
𝑒 𝜃𝑥
𝑦′′′
= 𝜃3
𝑒 𝜃𝑥
𝑦′′′ − 𝑦′′ = 𝜃3 𝑒 𝜃𝑥 − 𝜃2 𝑒 𝜃𝑥 = 0
𝜃2
𝑒 𝜃𝑥
𝜃 − 1 = 0
𝑒 𝜃𝑥
≠ 0 → 𝜃 = 0, 𝜃 = 1
Higher Orders Derivatives

43. First & Second Order Differentials
• If 𝒚 = 𝒇(𝒙) is differentiable on an interval then at any point of that
interval the derivative of 𝒇 can be defined as:
𝒚′
= 𝒇′
𝒙 =
𝒅𝒚
𝒅𝒙
= 𝐥𝐢𝐦
∆𝒙→𝟎
𝚫𝒚
𝚫𝒙
• This means when 𝚫𝒙 becomes “infinitesimal” (getting smaller
infinitely; ∆𝒙 → 𝟎), the ratio
𝚫𝒚
𝚫𝒙
approaches to the derivative of the
function, i.e. the difference between
𝚫𝒚
𝚫𝒙
and 𝒇′ 𝒙 is infinitesimal
itself and ignorable:
𝚫𝒚
𝚫𝒙
≈ 𝒇′
𝒙 𝒐𝒓 ∆𝒚 ≈ 𝒇′
𝒙 . ∆𝒙
• 𝒇′ 𝒙 . ∆𝒙 is called “ differential of 𝒚 ” and is shown by 𝒅𝒚, so:
∆𝒚 ≈ 𝒇′ 𝒙 . ∆𝒙 = 𝒅𝒚
As ∆𝒙 is an independent increment of 𝒙 we can always assume that
𝒅𝒙 = ∆𝒙; so we can re-write the above as ∆𝒚 ≈ 𝒇′
𝒙 . 𝒅𝒙 = 𝒅𝒚

44. • The geometric interpretation of 𝒅𝒚 and ∆𝒚 :
∆𝒚 represents the change in height of the curve and 𝒅𝒚 represents the
change in height of the tangent line when ∆𝒙 changes (see the graph)
Adopted fromhttp://www.cliffsnotes.com/math/calculus/calculus/applications-of-the-
derivative/differentials
So: 𝒅𝒚 = 𝒚′. 𝒅𝒙
Some rules:
If 𝒖 and 𝒗 are differentiable functions, then:
i. 𝒅 𝒄𝒖 = 𝒄. 𝒅𝒖 (c is constant)
ii. 𝒅 𝒖 ± 𝒗 = 𝒅𝒖 ± 𝒅𝒗 (can be extended
to more than two functions)
iii. 𝒅 𝒖. 𝒗 = 𝒗. 𝒅𝒖 + 𝒖. 𝒅𝒗 (extendable)
iv. 𝒅
𝒖
𝒗
=
𝒗.𝒅𝒖−𝒖.𝒅𝒗
𝒗 𝟐
First & Second Order Differentials

45. • Using the third rule of differentials, the second order differential of
𝒚 can be calculated, i.e. :
𝒅 𝟐
𝒚 = 𝒅 𝒅𝒚 = 𝒅 𝒚′
. 𝒅𝒙
= 𝒅𝒚′. 𝒅𝒙 + 𝒚′. 𝒅 𝒅𝒙
= 𝒚′′. 𝒅𝒙. 𝒅𝒙 + 𝒚′. 𝒅 𝟐 𝒙
= 𝒚′′. 𝒅𝒙 𝟐 + 𝒚′. 𝒅 𝟐 𝒙
As 𝒙 is not dependent on another variable and 𝒅𝒙 is a constant :
𝒅 𝟐 𝒙 = 𝒅 𝒅𝒙 = 𝟎
So, 𝒅 𝟐 𝒚 = 𝒚′′. 𝒅𝒙 𝟐 = 𝒚′′. 𝒅𝒙 𝟐 (or in the familiar form 𝒚′′ =
𝒅 𝟐 𝒚
𝒅𝒙 𝟐 )
Where 𝒅𝒙 𝟐 = 𝒅𝒙 𝟐 is always positive and the sign of 𝒅 𝟐 𝒚 depends
on the sign of 𝒚′′.
• Applying the same method we have 𝒅 𝒏 𝒚 = 𝒚(𝒏). 𝒅𝒙 𝒏 .
First & Second Order Differentials

46. Derivative and Optimisation of Functions
• Function 𝒚 = 𝒇 𝒙 is said to be an increasing function at
𝒙 = 𝒂 if at any small neighbourhood (∆𝒙) of that point:
𝑎 + ∆𝑥 > 𝑎 ↔ 𝑓 𝑎 + ∆𝑥 > 𝑓 𝑎
From the above inequality we can conclude that:
𝑓 𝑎+∆𝑥 −𝑓(𝑎)
∆𝑥
≈ 𝑓′(𝑎) > 0
So, the function is increasing
at 𝒙=𝒂 if 𝒇′(𝒂)>𝟎 , and
decreasing if 𝒇′(𝒂)<𝟎 .
Adopted from http://portal.tpu.ru/SHARED/k/KONVAL/Sites/English_sites/calculus/3_Geometric_f.htm
a a

47. • More generally, the function 𝒚 = 𝒇(𝒙) is increasing
(decreasing) in an interval if at any point in that interval
𝒇′ 𝒙 > 𝟎 ( 𝒇′ 𝒙 < 𝟎 ).
Derivative and Optimisation of Functions
Adopted from http://www.webgraphing.com/polynomialdefs.jsp

48. Derivative and Optimisation of Functions
• If the sign of 𝒇′
(𝒙) is changing when passing a point such as 𝒙 =
𝒂 (from negative to positive or vice versa) and 𝒚 = 𝒇(𝒙) is
differentiable at that point, It is very logical to think that 𝒇′
(𝒙)
at that point should be zero, i.e. : 𝒇′ 𝒂 = 𝟎. (in this case the
tangent line is horizontal)
• This point is called local (relative) maximum or local (relative)
minimum. In some books it is called critical point or extremum point.
http://www-rohan.sdsu.edu/~jmahaffy/courses/s00a/math121/lectures/graph_deriv/diffgraph.html
Not an extremum or critical point

49. • If 𝒇′ 𝒂 = 𝟎 but the sign of 𝒇′(𝒙) does not change when passing
the point 𝒙 = 𝒂, the point (𝒂, 𝒇 𝒂 ) is not a extremum or critical
point (point C in the previous slide).
• For a function which is differentiable in its domain(or part of that),
a sign change of 𝒇′
when passing a point is a sufficient evidence of
the point being a extremum point. Therefore, at that point 𝒇′(𝒙)
will be necessarily zero.
Necessary and Sufficient Conditions
𝒇′
𝒙 > 𝟎
𝒇′
𝒙 < 𝟎
𝑓′
𝑎 = 0
Adopted and altered from http://homepage.tinet.ie/~phabfys/maxim.htm/
𝒇′
(𝒙) > 𝟎
𝑓′
𝑏 = 0
𝒇′
𝒙 < 𝟎
a
b

50. • If a function is not differentiable at a point (see the graph, point
x=c) but the sign of 𝒇′ changes, it is sufficient to say the point is a
extremum point despite non-existence of 𝒇′(𝒙) .
Necessary and Sufficient Conditions
Adopted from http://www.nabla.hr/Z_IntermediateAlgebraIntroductionToFunctCont_3.htm
𝒇′
(𝒄) is not defined as it goes to infinity
These types of critical
points cannot be
obtained through
solving the equation
𝒇′ 𝒙 = 𝟎 as they are
not differentiable at
these points.

51. Second Derivative Test
• Apart from the sign change of 𝒇′
(𝒙) there is another test to
distinguish between extremums. This test is suitable for those
functions which are differentiable at least twice at the critical points.
• Assume that 𝒇′ 𝒂 = 𝟎; so, the point (𝒂, 𝒇 𝒂 ) is suspicious to be a
maximum or minimum. If 𝒇′′ 𝒂 > 𝟎, the point is a minimum point
and if 𝒇′′ 𝒂 < 𝟎, the point is a maximum point.
Adopted and altered from http://www.webgraphing.com/polynomialdefs.jsp
Inflection point
Concave Down
Concave up
𝑓′
𝑥 = 0
𝑓′
𝑥 = 0
𝑓′′
𝑥 = 0

52. Inflection Point & Concavity of Function
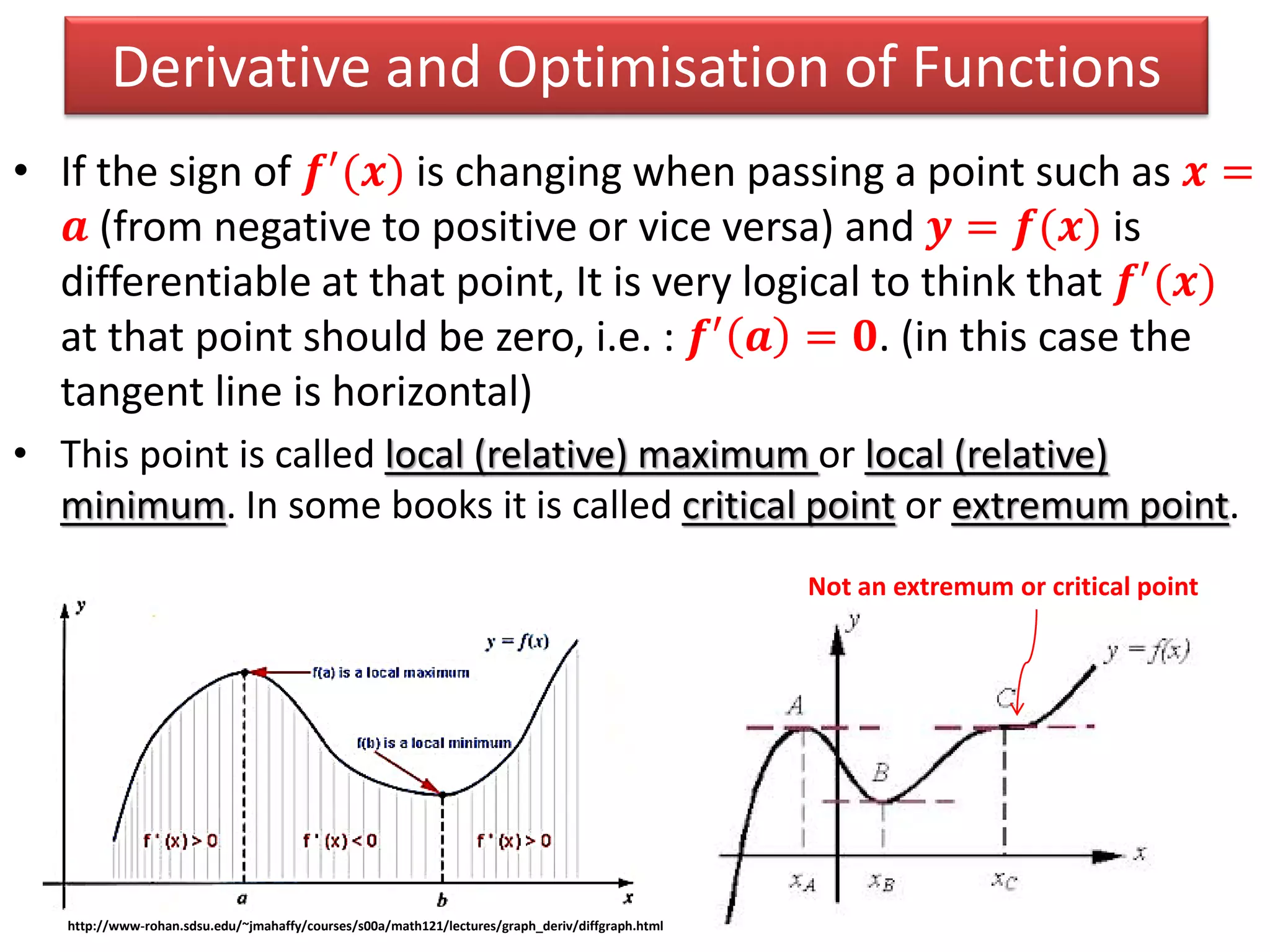
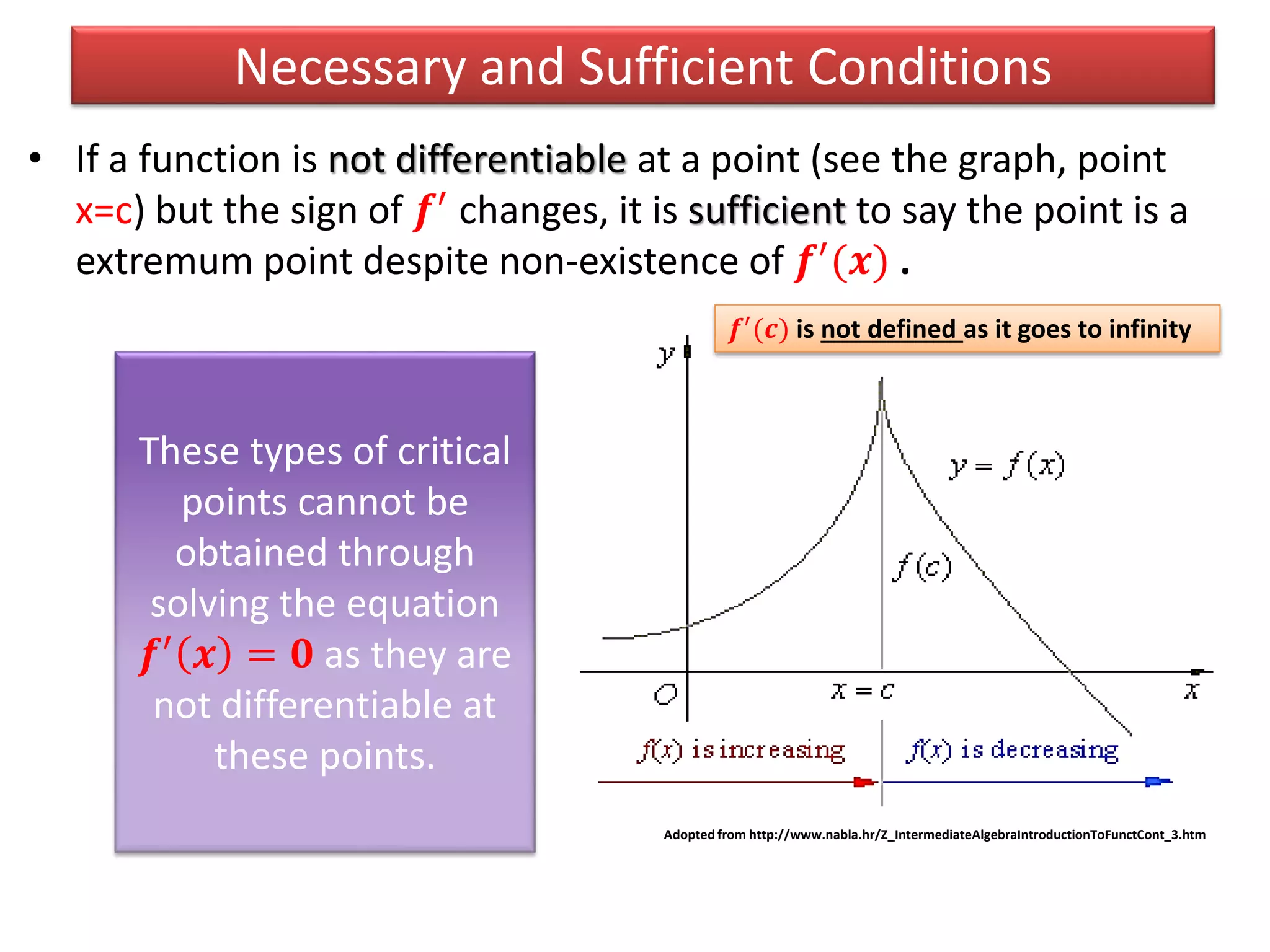
• If 𝒇′ 𝒂 = 𝟎 and at the same time 𝒇′′ 𝒂 = 𝟎, we need other tests
to find out the nature of the point. It could be a extremum point
[e.g. 𝒚 = 𝒙 𝟒
, which has minimum at 𝒙 = 𝟎]or just an inflection
point (where the tangent line crosses the graph of the function and
separate that to two parts; concave up and concave down)
Adopted and altered from http://www.ltcconline.net/greenl/courses/105/curvesketching/SECTST.HTM Adopted from http://www.sparkle.pro.br/tutorial/geometry
𝑓′′ 𝑥 = 0
𝑓′ 𝑥 > 0
Concave Down
Concave up

53. Some Examples
o Find extremums of 𝒚 = 𝒙 𝟑 − 𝟑𝒙 𝟐 + 𝟐, if any.
To find the points which could be our extremums (critical points) we
need to find the roots of this equation: 𝒇′ 𝒙 = 𝟎,
So, 𝒇′ 𝒙 = 𝟑𝒙 𝟐 − 𝟔𝒙 = 𝟎 → 𝟑𝒙 𝒙 − 𝟐 = 𝟎
→ 𝒙 = 𝟎, 𝒙 = 𝟐
Two points 𝑨(𝟎, 𝟐) and 𝑩(𝟐, −𝟐) are possible extremums.
Sufficient condition(1st method): As the sign of 𝒚′ = 𝒇′(𝒙) changes
while passing through the points there is a maximum and a minimum.
𝒙 −∞ +∞
𝑦′ + − +
𝑦
0 2
2 -2
Max Min

54. Some Examples
• Sufficient condition (2nd method): we need to find the sign of 𝒇′′(𝒙)
at those critical points:
𝒇′′ 𝒙 = 𝟔𝒙 − 𝟔
𝒇′′ 𝒙 = 𝟎 = −𝟔 → 𝑨 𝟎, 𝟐 𝒊𝒔 𝒎𝒂𝒙𝒊𝒎𝒖𝒎
𝒇′′ 𝒙 = 𝟐 = 𝟔 → 𝑩 𝟐, −𝟐 𝒊𝒔 𝒎𝒊𝒏𝒊𝒎𝒖𝒎
o Find the extremum(s) of 𝒚 = 𝟏 −
𝟑
𝒙 𝟐, if any.
𝒚′ =
−𝟐
𝟑 𝟑
𝒙
Although 𝒚′ cannot be zero but its sign changes when passing through
𝒙 = 𝟎, so the function has a maximum at point 𝑨(𝟎, 𝟏). The second
method of the sufficient condition cannot be used here. Why?
𝒙 −∞ +∞
𝑦′ +
𝑦
0
1
Max