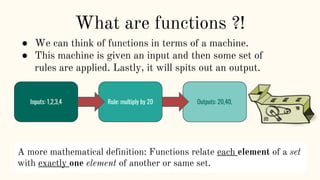
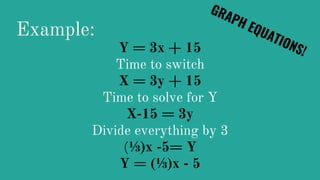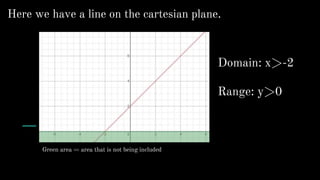
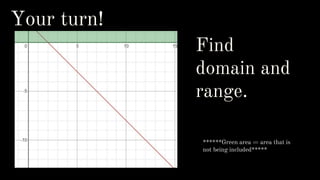
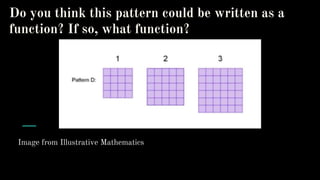
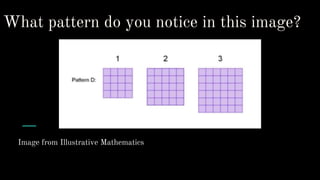
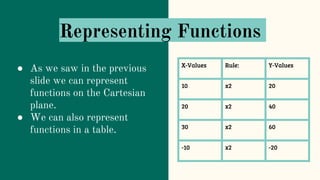
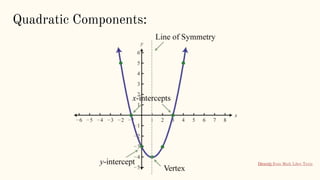
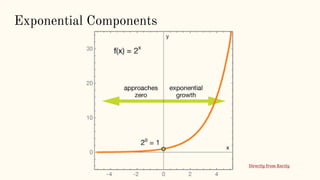
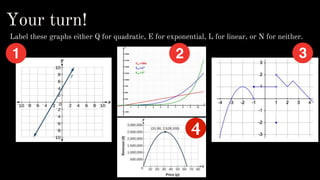
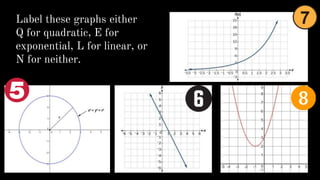
This document introduces functions and key concepts related to functions such as: - Domain and range - Representing functions in tables, graphs, and equations - Identifying linear, quadratic, and exponential functions - Adding, subtracting, and inverting functions It provides examples and interactive exercises to help explain these fundamental function concepts.

1. Functions
Lobomath

2. Here’s a
warm up
activity to
introduce our
lesson!

3. What pattern do you notice in this image?
Image from Illustrative Mathematics

4. Do you think this
pattern could be
written as a
function?
The answer is YES !
Specifically a trinomial and a
quadratic!
Quadratic function:
Y=(x+3)^2
BUT,
What on earth are trinomials
and quadratics!?

5. Stay tuned to find out…
By the end of this lesson you will be
able to solve this pattern problem on
your own, as well as other real-
world problems involving functions!

6. Here are the Content Standards:
1. Make sense of problems and persevere in
solving them.
2. Reason abstractly and quantitatively.
4. Model with mathematics.
5. Use appropriate tools strategically.
7. Look for and make use of structure.
8. Look for and express regularity in repeated
reasoning.

7. But…
What will we be
learning in this
lesson?

8. Learning
objectives:
● Domain and Range
relations.
● Creating functions.
● Representing functions
in tables and graphs.
● Identifying functions
through vertical line test.
● Evaluating functions.
● Add/subtract functions
● Inverse functions

9. Before beginning let’s learn about sets...
● A set is a collection of things.
● Each thing in the set is an element.
● Set notation varies depending on the math class.
● You can write sets in brackets.
● For example: {a,b,c,d}
● In the example set, “a” is an element of the set (a€S)
● Here is a set from a grocery store —->
{“apples”,”pears”,”bananas”,”oranges”}
● Now come up with your own set !

10. ● We will be dealing with the set of real numbers in this class.
● Real numbers ……-5,-4,-3,-2,-1,0,1,2,3,4,5 ……..
● On a number line we can see it goes on all the way to infinity
on the right side and all the way to negative infinity on the
left side.
● We can also have the set of nothing { }, also known as the
null or empty set.

11. What are functions ?!
● We can think of functions in terms of a machine.
● This machine is given an input and then some set of
rules are applied. Lastly, it will spits out an output.
A more mathematical definition: Functions relate each element of a set
with exactly one element of another or same set.
Rule: multiply by 20Inputs: 1,2,3,4 Outputs: 20,40,

12. Domain and Range
Domain: Set of all possible inputs.
In other words all possible x-values (independent variable)
Take a look at this number line. The line
represents x-
values starting at
-1 and continuing
to infinity.
Range: Set of all possible output values (dependent
variable-dependent on the x-values).
● To view the range I will be showing you a line on a cartesian
plane (x and y plane). This is a coordinate plane, the form is (x,y)

13. Here we have a line on the cartesian plane.
Domain: x>-2
Range: y>0
Green area = area that is not being included

14. Your turn!
******Green area = area that is
not being included*****
Find
domain and
range.

15. Representing Functions
● As we saw in the previous
slide we can represent
functions on the Cartesian
plane.
● We can also represent
functions in a table.
X-Values Rule: Y-Values
10 x2 20
20 x2 40
30 x2 60
-10 x2 -20

16. Creating Functions
● There are many different types of functions. The one you will
become most familiar with is a linear equation.
*function=equation
● The general form of a linear equations is:
● Y = mx+b
Let’s break this down.
● Y is our dependent variable, it depends on what number we put in
for x.
● M is out slope of the line. Slope is the proportion it rise/run.
● X is our independent variable.
● B is the y-intercept of our line.
Lines could be monomials or binomials. Which simply refers to the
quantity of terms in your function.

17. Watch this video to learn about the difference between
monomials,binomials,trinomials and polynomials

18. Identifying Functions
We will be working with primarily 3 functions.
1. Quadratics
2. Linear
3. Exponential
1 2 3

19. Quadratic Components:
Directly from Math Libre Texts

20. Exponential Components
Directly from Xactly

21. Your turn!
Label these graphs either Q for quadratic, E for exponential, L for linear, or N for neither.

22. Label these graphs either
Q for quadratic, E for
exponential, L for linear, or
N for neither.

23. Brain Break
On a blank sheet of paper attempt to draw
an image containing all of these shapes:
-square
-triangle
-circle
Example on next slide

25. Adding and Subtracting Functions:
Now that we have the basics down, we can learn
how to add and subtract functions.
Steps:
1. Identify the components of the function. ([x]
+ [3] and [3x] - [7])
2. Then depending on the rule, add or subtract
each individual SIMILAR component. By
similar we mean, like terms.
3. Add/subtract the numerical component and
variables ( for addition; 4x - 4 & for
subtraction; -2x+10)
4. Check to see if it could be simplified.

26. Your turn!
Add and subtract the functions!
1)y = 2x^2 + 5x +12
2)y = 9x^2 + 3x + 3

27. Inverting Functions
Process T2SS (Time to switch and solve)
● When you invert functions you will
need to keep in mind the process of
T2SS.
● Once you have your functions the
first step will be to switch the x and
the y.
● The function will look funny so we
must solve it in terms of Y so that
we can recognize its original form.
Here is the difference between a
function and its inverse. Blue line is
the inverse.

28. Example:
Y = 3x + 15
Time to switch
X = 3y + 15
Time to solve for Y
X-15 = 3y
Divide everything by 3
(⅓)x -5= Y
Y = (⅓)x - 5

29. Your turn!
Invert the function
Y = 2(x-7) + 6

30. Image from Illustrative Mathematics
Do you think this pattern could be written as a
function? If so, what function?

31. Solution:
Observations:
● Image 1—> 16 squares —> 4x4 =16 or 4^2
● Image 2 —> 25 squares —> 5x5 =25 or 5^2
● Image 3 —> 36 squares —> 6x6 =36 or 6^2
● Image 4 —> 49 squares —> 7x7 =49 or 7^2
● Image n —> y squares —> nxn = y or n^2

32. Solution:
Where n is a symbol for image number and y is the total
squares.
The equation Y = n^2 —> why does this not work?
Let’s try image 2.
25 = (2)^2 —> 25 ≠ 4.
Therefore something is missing. Let’s look at image 1.
16 = (1)^2 —> 16≠1. But we say earlier that 4^2
works.
So let’s change our equation to satisfy the conditions.
Y = (n+3)^2.
Correct we got it!

33. T.O.T.D Question:
Do you think this pattern could be written as
a function? If so, what function?
Image from Illustrative Mathematics