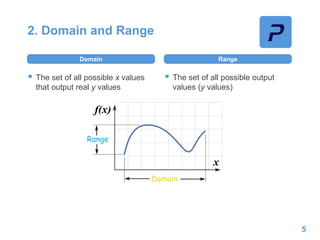
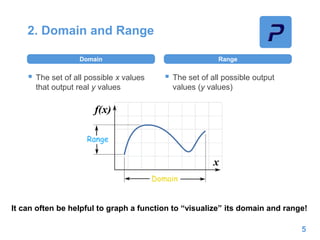
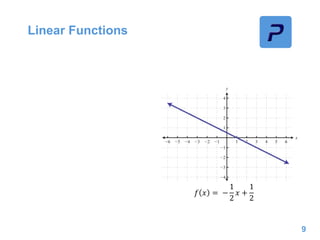
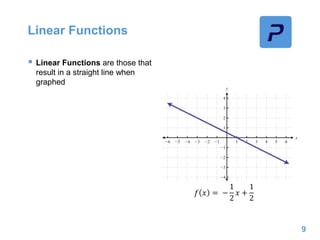
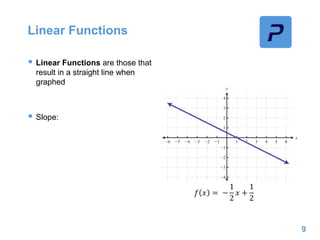
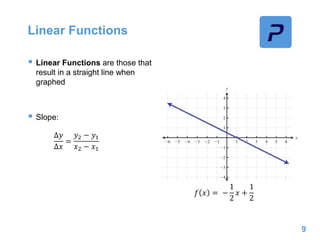
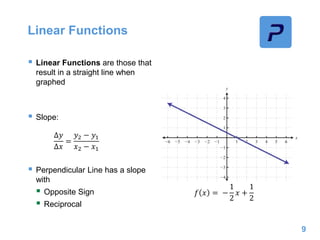
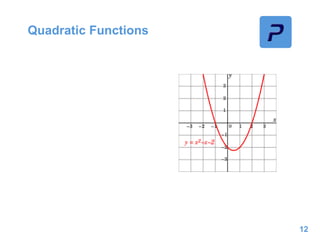
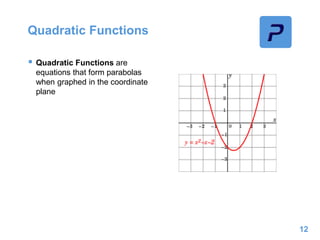
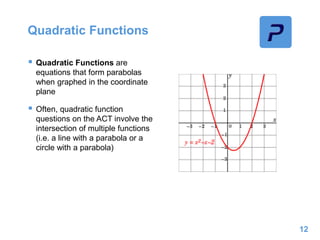
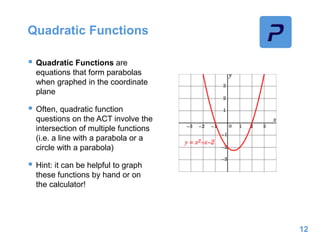
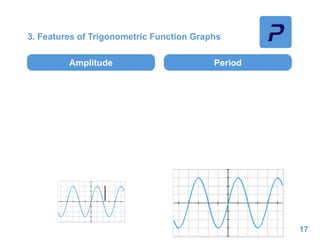
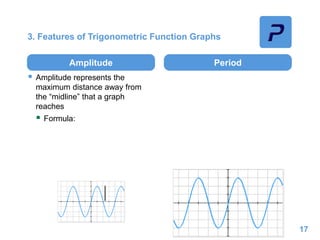
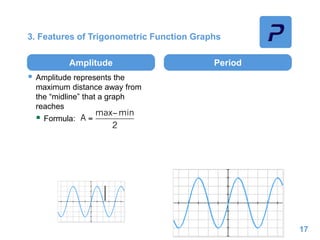
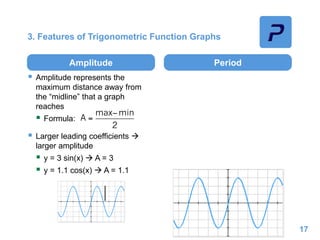
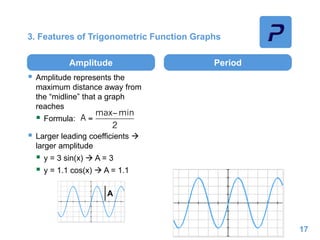
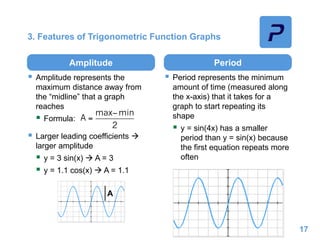
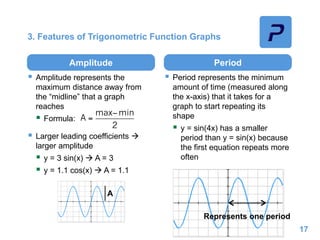
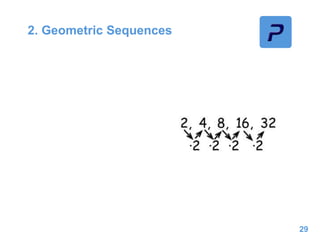
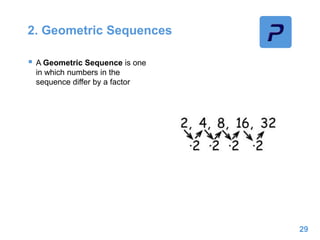
This document provides an overview of different types of functions that may be assessed on the ACT exam, including linear, quadratic, trigonometric, logarithmic, and exponential functions. It discusses key concepts for each type of function such as domain and range, asymptotes, amplitude and period for trig functions, and properties of logarithmic and exponential growth/decay functions. Examples are provided to illustrate how to work with each function type, including solving equations, finding features of graphs, and recognizing standard forms.