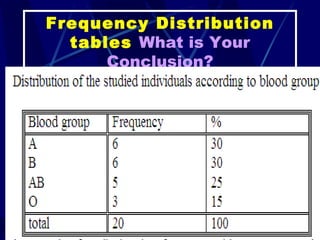
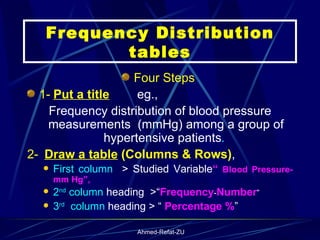
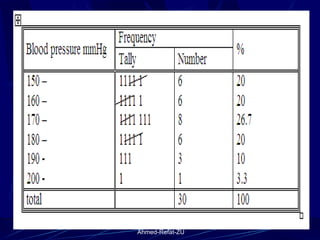
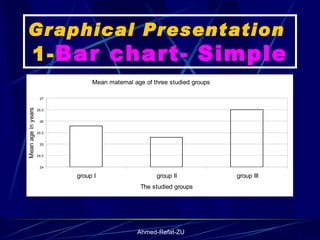
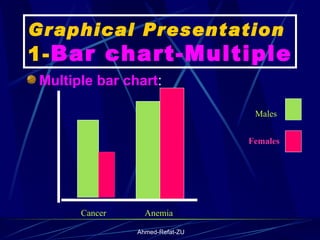
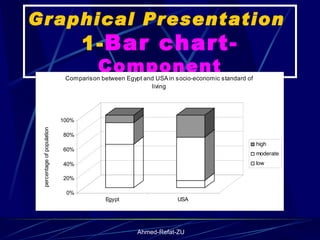
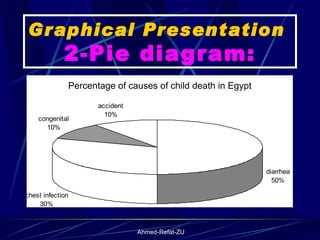
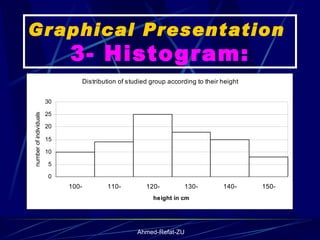
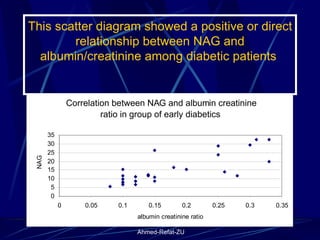
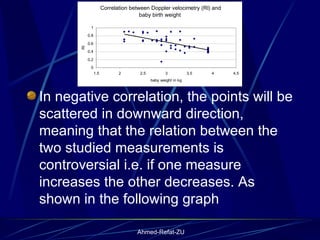
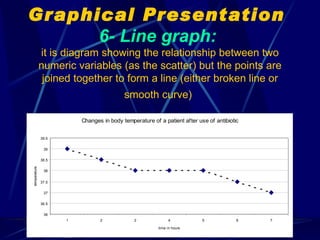
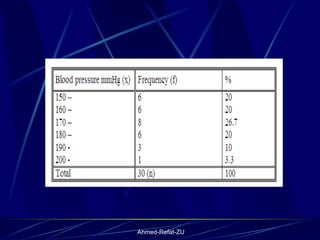
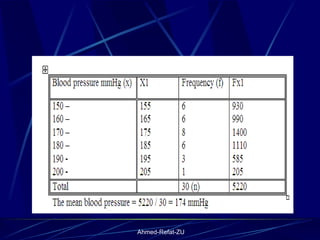
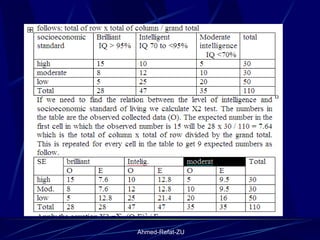
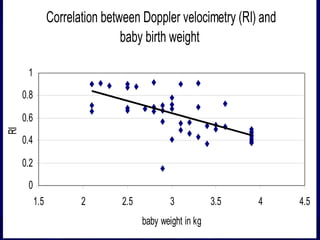
The document provides an overview of basic statistical concepts and methods, emphasizing the definition of statistics as the science of dealing with numbers and its application in organizing and analyzing data. It discusses the types of data, methods of data presentation including tables and graphs, and measures of central tendency such as mean, median, and mode. Additionally, it highlights the importance of statistical analysis in medical research, community health evaluations, and compares health metrics over time and among different populations.