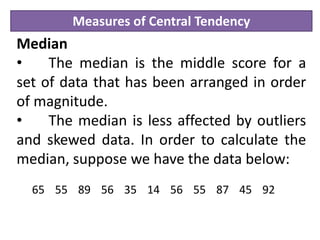
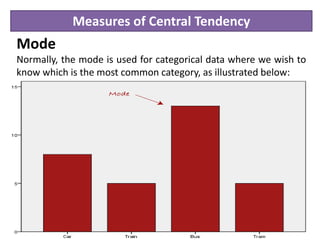
Descriptive statistics are used to describe and summarize the basic features of data through measures of central tendency like the mean, median, and mode, and measures of variability like range, variance and standard deviation. The mean is the average value and is best for continuous, non-skewed data. The median is less affected by outliers and is best for skewed or ordinal data. The mode is the most frequent value and is used for categorical data. Measures of variability describe how spread out the data is, with higher values indicating more dispersion.