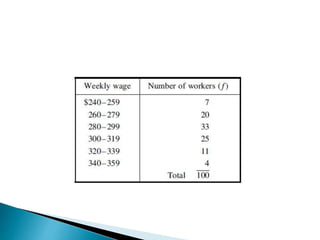
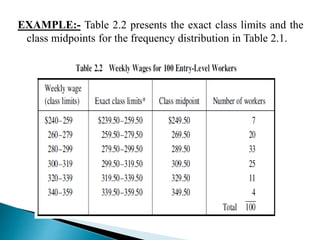
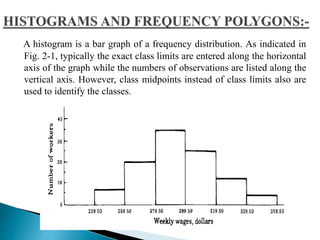
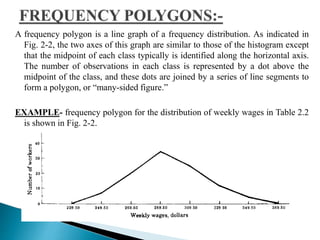
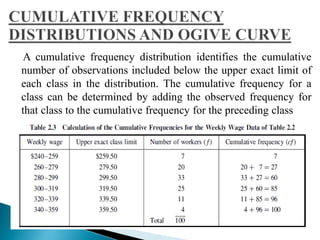
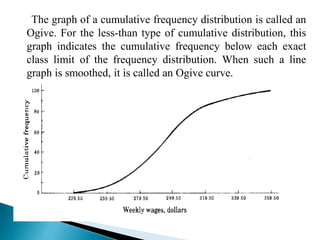
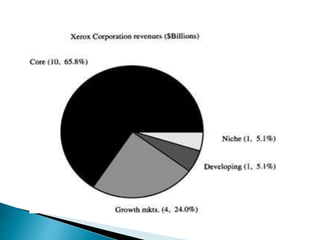
This document discusses statistics and their uses in various fields such as business, health, learning, research, social sciences, and natural resources. It provides examples of how statistics are used in starting businesses, manufacturing, marketing, and engineering. Statistics help decision-makers reduce ambiguity and assess risks. They are used to interpret data and make informed decisions. However, statistics also have limitations as they only show averages and may not apply to individuals.

1. Prof. Rajkumar Teotia
Institute of Advanced Management and Research (IAMR)
Address: 9th Km Stone, NH-58, Delhi-Meerut Road, Duhai,Ghaziabad (U.P)
- 201206
Ph:0120-2675904/905 Mob:9999052997 Fax: 0120-2679145
e mail: rajkumarteotia@iamrindia.com

3.  Collection of methods for planning experiments, obtaining
data, and then organizing, summarizing, presenting, analyzing,
interpreting, and drawing conclusions
 Statistics refers to the body of techniques used for collecting,
organizing, analyzing, and interpreting data. The data may be
quantitative, with values expressed numerically, or they may be
qualitative, with characteristics such as consumer preferences
being tabulated. Statistics is used in business to help make
better decisions by understanding the sources of variation and
by uncovering patterns and relationships in business data.

4.  Statistics are the aggregates of facts
 Statistics are affected by a number of factors
 Statistics must be reasonably accurate
 Statistics must be collected in a systematic manner
 Collected in a systematic manner for a pre-determined purpose
 Lastly, Statistics should be placed in relation to each other

5.  Statistics are the aggregates of facts:-
It means a single figure is not statistics. For example, national income
of a country for a single year is not statistics but the same for two or
more years is statistics.
 Statistics are affected by a number of factors:-
For example, sale of a product depends on a number of factors such as
its price, quality, competition, the income of the consumers, and so on.
 Statistics must be reasonably accurate:-
Wrong figures, if analyzed, will lead to erroneous conclusions. Hence,
it is necessary that conclusions must be based on accurate figures.
 Statistics must be collected in a systematic manner:-
If data are collected in a haphazard manner, they will not be reliable and
will lead to misleading conclusions.

6.  Collected in a systematic manner for a pre-determined
purpose
 Statistics should be placed in relation to each other:-
If one collects data unrelated to each other, then such data
will be confusing and will not lead to any logical conclusions.
Data should be comparable over time and over space.

7. There are two main branches of statistics
 Descriptive Statistics
 Inferential Statistics

8. Descriptive statistics include the techniques that are used to
summarize and describe numerical data for the
Purpose of easier interpretation
EXAMPLE-The
monthly sales volume for a product during the past year can
be described and made meaningful by
Preparing a bar chart or a line graph. The relative sales by
month can be highlighted by calculating an index number for
each month such that the deviation from 100 for any given month
indicates the percentage deviation of sales in that month as
compared with average monthly sales during the entire year.

9. Inferential statistics include those techniques by which
decisions about a statistical population or process are made
based only on a sample having been observed. Because
such decisions are made under conditions of uncertainty, the
use of probability concepts is required
EXAMPLE-In
order to estimate the voltage required to cause an
electrical device to fail, a sample of such devices can Be
subjected to increasingly higher voltages until each device
fails. Based on these sample results, the probability of
failure at various voltage levels for the other devices in the
sampled population can be estimated.

10. Statistics starts with a question, not with
data/information
 Every time we use statistic to find the solution for a question.
 Statistics are what decision makers can use to reduce ambiguity by
qualifying it.
All Statistics are based on data
 Data are what we hear, see, smell, taste, touch, etc.
 Data requires measuring
 Statistics are designed to transform data into information
 Make decisions using that information.
 Statistics are about and used to measure/assess risk of the decision.

11.  Business and Industry
 Health and Medicine
 Learning
 Research
 Social Statistics
 Natural Resources

12.  Statistics to start a Business
 Statistics to manufacturing
 Statistics to marketing
 Statistics to Engineering

13. Whether you are writing a business plan, feasibility
study, advertising and marketing campaign, or even
still deciding on what kind of business to start, start by
looking at what is already happening in the field or
industry you are interested in.
Statistics are not magic formulas for success, but they
can give you important clues about how others are or
failing.

14. In this process we use statistic to understand the number
of products we have to produce and what are the new
strategies we have to apply in future. It also gives an
overview of the market.

15. In marketing we use statistic in many ways banking the
money you have in your business bank account can often
provoke actions that are regretted at a later time. For
example, if you have a healthy balance, you may decide to
splash out on a purchase or investment that will in time,
leave your account dangerously low: when money comes
in, it is not unusual for all common sense to go out of the
window…a bit extreme you may think!

16. Engineers apply physical and chemical laws and
mathematics to design, develop, test, and supervise
various products and services. Engineers perform tests
to learn how things behave under stress, and at what
point they might Fail. As engineers perform
experiments, they collect data that can be used to
explain relationships better and to reveal information
about the quality of products and services they provide.

17. Medical statistics deals with applications of including
epidemiology, public health find data on indicators of the
nation's health, such smoking drinking and drug use, and
abortion statistics.
This is of particular importance when attempting to determine
whether the pharmacological effect of one drug is superior to
another which clearly has implications for drug development
Therefore, it is essential for pharmacologists to have an
understanding of the uses of the statistics.

18. The techniques of statistics can prove to be valuable tools for
teachers of to interpret statistics is advantageous to analyze lab
results, book and journal articles, and as an aid in approaching
problem-solving scientifically. Statistics will allow you to
critically evaluate your students, your teaching, and the results
of educational research.

19. The word researches are depending in statistics, when we
found any data from research we analyze and make decisions
using statics. These are the examples for government
researches.
 Research and Development: DOE Could Enhance the
Project Selection Process for Government Oil and Natural
Gas Research.
 Bureau of Government Research wants 'realistic'
development strategy

20. Social statistics is the use of statistical measurement systems to
study human behavior in a social environment. This can be
accomplished through polling a particular group of people,
evaluating a particular subset of data obtained about a group of
people, or by observation and statistical analysis of a set of data
that relates to people and their behaviors.
Often, social scientists are employed in the evaluation of the
quality of services of a particular group or organization, in
analyzing behaviors of groups of people in their environment and
special situations, or even in determining the wants or needs of
people through statistical sampling.

21.  Child-bearing, Child and elderly populations
 Housing and Human settlements
 Education and Literacy
 Income , economic activity and Unemployment

22.  Health, nutrition and educational level in country.
 To identify the strength of working people.
 To planning the future

23.  Identify problems in housing planning.
 to settle the problems in slums.

24.  Study about the current education system in country.
 Develop the subject planning
 Future employment planning.

25.  To understand about savings and investment.
 introduce future investing systems

26. Statistics are used in the scientific study of agriculture as
a tool to determine if the differences in variables are real
or due to chance. This translates to the farmer to let him
know with confidence which varieties are better than
other varieties or which fertilizer treatments will give
better yields than others. In many countries in agriculture
they use so many statistical researches to do their
agriculture successfully. These are some of projects that
some countries are managed.

27.  There are certain phenomena or concepts where statistics cannot be
used. This is because these phenomena or concepts are not
amenable to measurement. For example, beauty, intelligence,
courage cannot be quantified. Statistics has no place in all such
cases where quantification is not possible.
 Statistics reveal the average behavior, the normal or the general
trend. An application of the 'average' concept if applied to an
individual or a particular situation may lead to a wrong conclusion
and sometimes may be disastrous.
For example, one may be misguided when told that the average
depth of a river from one bank to the other is four feet, when there
may be some points in between where its depth is far more than
four feet. On this understanding, one may enter those points having
greater depth, which may be hazardous.

28.  Since statistics are collected for a particular purpose, such data may
not be relevant or useful in other situations or cases. For example,
secondary data (i.e., data originally collected by someone else) may
not be useful for the other Person.
 Statistics are not 100 per cent precise as is Mathematics or
Accountancy. Those who use statistics should be aware of this
limitation.
 In statistical surveys, sampling is generally used as it is not
physically possible to cover all the units or elements comprising the
universe
 At times, association or relationship between two or more variables
is studied in statistics, but such a relationship does not indicate cause
and effect' relationship. It simply shows the similarity or
dissimilarity in the movement of the two variables

29. In statistics, data are classified into two broad categories:
 Quantitative data.
 Qualitative data.

30. Quantitative data are those that can be quantified in definite
units of measurement. These refer to characteristics whose
successive measurements yield quantifiable observations.
Depending on the nature of the variable observed for
measurement.
Quantitative data can be further categorized as
 Continuous Data
 Discrete Data.

31. Continuous data represent the numerical values of a
continuous variable. A continuous variable is the one that can
assume any value between any two points on a line segment,
thus representing an interval of values. The values are quite
precise and close to each other, yet distinguishably different.
All characteristics such as weight, length, height, thickness,
velocity, temperature, tensile strength, etc., represent
continuous variables. Thus, the data recorded on these and
similar other characteristics are called continuous data

32. Discrete data are the values assumed by a discrete variable. A
discrete variable is the one whose outcomes are measured in
fixed numbers. Such data are essentially count data. These are
derived from a process of counting, such as the number of items
possessing or not possessing a certain characteristic. The
number of customers visiting a departmental store every day,
the incoming flights at an airport, and the defective items in a
consignment received for sale, are all examples of discrete data.

33. Qualitative data refer to qualitative characteristics of a subject
or an object. A characteristic is qualitative in nature when its
observations are defined and noted in terms of the presence or
absence of a certain attribute in discrete numbers.
These data are further classified as
 Nominal Data
 Rank data

34. Nominal data are the outcome of classification into two or
more categories of items or units comprising a sample or a
population according to some quality characteristic.
Classification of students according to sex (as males and
females), of workers according to skill (as skilled, semi-skilled,
and unskilled), and of employees according to the
level of education (as matriculates, undergraduates, and post-graduates),
all result into nominal data. Given any such basis
of classification, it is always possible to assign each item to a
particular class and make a summation of items belonging to
each class. The count data so obtained are called nominal
data.

35. Rank data, on the other hand, are the result of assigning
ranks to specify order in terms of the integers 1,2,3, ..., n.
Ranks may be assigned according to the level of
performance in a test. a contest, a competition, an
interview, or a show. The candidates appearing in an
interview, for example, may be assigned ranks in integers
ranging from I to n, depending on their performance in
the interview. Ranks so assigned can be viewed as the
continuous values of a variable involving performance as
the quality characteristic.

36. Data sources could be seen as of two types, viz., secondary
and primary. The two can be defined as under:
(i) Secondary data: They already exist in some form:
published or unpublished - in an identifiable secondary
source. They are, generally, available from published
source(s), though not necessarily in the form actually
required.
(ii) Primary data: Those data which do not already exist in
any form, and thus have to be collected for the first time
from the primary source(s). By their very nature, these data
require fresh and first-time collection covering the whole
population or a sample drawn from it.

37. FREQUENCY DISTRIBUTIONS:-
A frequency distribution is a table in which possible values for
a variable are grouped into classes, and the number of
observed values which fall into each class is recorded. Data
organized in a frequency distribution are called grouped data.
In contrast, for ungrouped data every observed value of the
random variable is listed.
EXAMPLE 1. A frequency distribution of weekly wages is
shown in Table 2.1. Note that the amounts are reported to the
nearest dollar. When a remainder that is to be rounded is
“exactly 0.5” (exactly $0.50 in this case), the convention is to
round to the nearest even number. Thus a weekly wage of
$259.50 would have been rounded to $260 as part of the data-grouping
process.

39. CLASS INTERVALS:-
The class interval identifies the range of values included
within a class and can be determined by subtracting the
lower exact class limit from the upper exact class limit for
the class. When exact limits are not identified, the class
interval can be determined by subtracting the lower stated
limit for a class from the lower stated limit of the adjoining
next-higher class. Finally, for certain purposes the values in a
class often are represented by the class midpoint, which can
be determined by adding one-half of the class intervals to the
lower exact limit of the class.

40. EXAMPLE:- Table 2.2 presents the exact class limits and the
class midpoints for the frequency distribution in Table 2.1.

41. A histogram is a bar graph of a frequency distribution. As indicated in
Fig. 2-1, typically the exact class limits are entered along the horizontal
axis of the graph while the numbers of observations are listed along the
vertical axis. However, class midpoints instead of class limits also are
used to identify the classes.

42. A frequency polygon is a line graph of a frequency distribution. As indicated in
Fig. 2-2, the two axes of this graph are similar to those of the histogram except
that the midpoint of each class typically is identified along the horizontal axis.
The number of observations in each class is represented by a dot above the
midpoint of the class, and these dots are joined by a series of line segments to
form a polygon, or “many-sided figure.”
EXAMPLE- frequency polygon for the distribution of weekly wages in Table 2.2
is shown in Fig. 2-2.

43. A cumulative frequency distribution identifies the cumulative
number of observations included below the upper exact limit of
each class in the distribution. The cumulative frequency for a
class can be determined by adding the observed frequency for
that class to the cumulative frequency for the preceding class

44. The graph of a cumulative frequency distribution is called an
Ogive. For the less-than type of cumulative distribution, this
graph indicates the cumulative frequency below each exact
class limit of the frequency distribution. When such a line
graph is smoothed, it is called an Ogive curve.

45. A pie chart is a pie-shaped figure in which the pieces of the pie
represent divisions of a total amount, such as the distribution of a
company’s sales dollar. A percentage pie chart is one in which the values
have been converted into percentages in order to make them easier to
compare
EXAMPLE:- Figure 2-12 is a pie chart depicting the revenues and the
percentage of total revenues for the Xerox Corporation during a recent
year according to the categories of core business (called “Heartland” by
Xerox), growth markets; developing countries, and niche opportunities