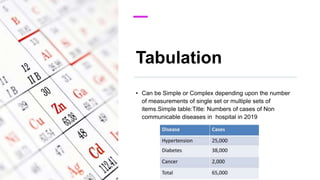
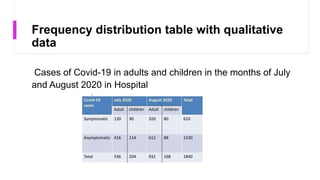
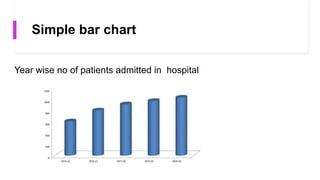
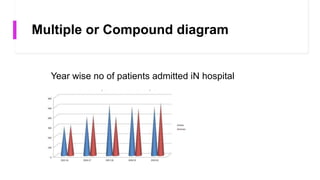
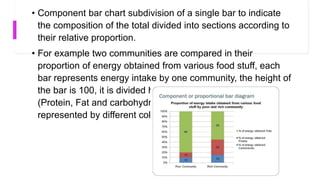
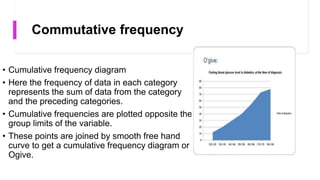
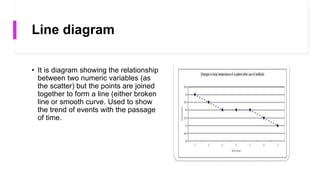
The document discusses principles and methods for presenting data, including: - Data should be arranged to interest readers while maintaining important details simply. - The two basic methods are tabulation and charts/diagrams. - Tabulation rules include numbering, titling, defining headings clearly. - Common charts are pie charts, bar diagrams, histograms, frequency polygons, and scatter diagrams. Each has strengths for different data types.

1. Presentation of
data

2. Principles of
presentation of data
• Data should be arranged in such a way that it will arouse
interest in reader.
• The data should be made sufficiently concise without
losing important details.
• The data should presented in simple form to enablethe
reader to form quick impressions and to drawsome
conclusion, directly or indirectly. Should facilitate further
statistical analysis.It should define the problem and
suggest its solution

3. Methods of
presentation of data
• The first step in statistical analysis is to present data in an
easy way to be understood. The two basic ways for data
presentation are
• Tabulation
• charts and diagram.

5. Rules and guidelines
for tabular
• Table must be numberedBrief and self explanatory title must be given to
each table.The heading of columns and rows must be clear, sufficient,
concise and fully defined.The data must be presented according to size of
importance, chronologically, alphabetically geographically If data includes
rate or proportion, mention the denominator.
• Table should not be too large.Figures needing comparison should be
placedas close as possible.The classes should be fully defined, should not
lead to any ambiguity.
• The classes should be exhaustive i.e. Should include all the given
values.The classes should be mutually exclusive and non overlapping.

6. • The classes should be of equal width or class interval
should be sameOpen ended classes should be avoided
as far as possible.The number of classes should be
neither too large nor too small. Can be 10-20
classes.Formula for number of classes(K):.

7. Tabulation
• Can be Simple or Complex depending upon the number
of measurements of single set or multiple sets of
items.Simple table:Title: Numbers of cases of Non
communicable diseases in hospital in 2019

8. Frequency distribution table with qualitative
data
Cases of Covid-19 in adults and children in the months of July
and August 2020 in Hospital

9. Charts and diagrams
Graphic presentations used to illustrate and clarify information.
Are essential in presentation of scientific data and diagrams
are complementary to summarize these tables in an easy,
attractive and simple way.

10. • Charts and diagrams are useful methods of presenting simple data.
• They have powerful impact on imagination of people.
• Gives information at a glance. Diagrams are better retained in memory
than statistical table.
• However graphs cannot be substituted for statistical table, because the
graphs cannot have mathematical treatment where as tables can be
treated mathematically.
• Whenever graphs are compared the difference in the scale should be
noted.
• It should be remembered that a lot of details and accuracy of original
data is lost in charts and diagrams, and if we want the real study, we
have to go back to the original data

11. Common diagrams
• Pie chart
• Simple bar diagram
• Multiple bar diagram
• Component bar diagram or subdivided bar
• diagram
• Histogram
• Frequency polygon
• Frequency curve
• O give curve
• Scatter diagram
• Line diagram
• Pictogram
• Statistical maps

12. Bar diagrams
• Widely used, easy to prepare tool for comparing categories of mutually exclusive discrete data.
• Different categories are indicated on one axis
• and frequency of data in each category on
• another axis.
• Length of the bar indicate the magnitude of the frequency of the character to be compared.
• Spacing between the various bar should be equal to half of the width of the bar.
• 3 types of bar diagram:
• Simple Multiple
• compound Component
• proportional

13. Simple bar chart
Year wise no of patients admitted in hospital

14. Multiple or Compound diagram
Year wise no of patients admitted iN hospital

15. • Component bar chart subdivision of a single bar to indicate
the composition of the total divided into sections according to
their relative proportion.
• For example two communities are compared in their
proportion of energy obtained from various food stuff, each
bar represents energy intake by one community, the height of
the bar is 100, it is divided horizontally into 3 components
(Protein, Fat and carbohydrate) of diet, each component is
represented by different color or shape

16. Histogram
• Used for Quantitative, Continuous,
Variables. It is used to present variables
which have no gaps e.g age, weight,
height, blood pressure, blood sugar etc.
• It consist of a series of blocks.
• The class intervals are given along
horizontal axis and the frequency along the
vertical axis.

17. Frequency Polygon
• Frequency polygon is an area diagram of
frequency distribution over a histogram.
• It is a linear representation of a frequency
table and histogram, obtained by joining
the mid points of the hitogram blocks.
• Frequency is plotted at the central point of
a group

18. Commutative frequency
• Cumulative frequency diagram
• Here the frequency of data in each category
represents the sum of data from the category
and the preceding categories.
• Cumulative frequencies are plotted opposite the
group limits of the variable.
• These points are joined by smooth free hand
curve to get a cumulative frequency diagram or
Ogive.

19. Scatter/dot diagram
• Also called as Correlation diagram it is useful to represent
the relationship between two numeric measurements,
each observation being represented by a point
corresponding to its value on each axis.
• In negative correlation, the points will be scattered in
downward direction, meaning that the relation between
the two studied measurements is controversial i.e. If one
measure increases the other decreases While in positive
correlation, the points will be scattered in upward
direction.

20. Line diagram
• It is diagram showing the relationship
between two numeric variables (as
the scatter) but the points are joined
together to form a line (either broken
line or smooth curve. Used to show
the trend of events with the passage
of time.

21. Pie diagram
• Consist of a circle whose area represents the total frequency
(100%) which is divided into segments.
• Each segment represents a proportional composition of the
total frequency.