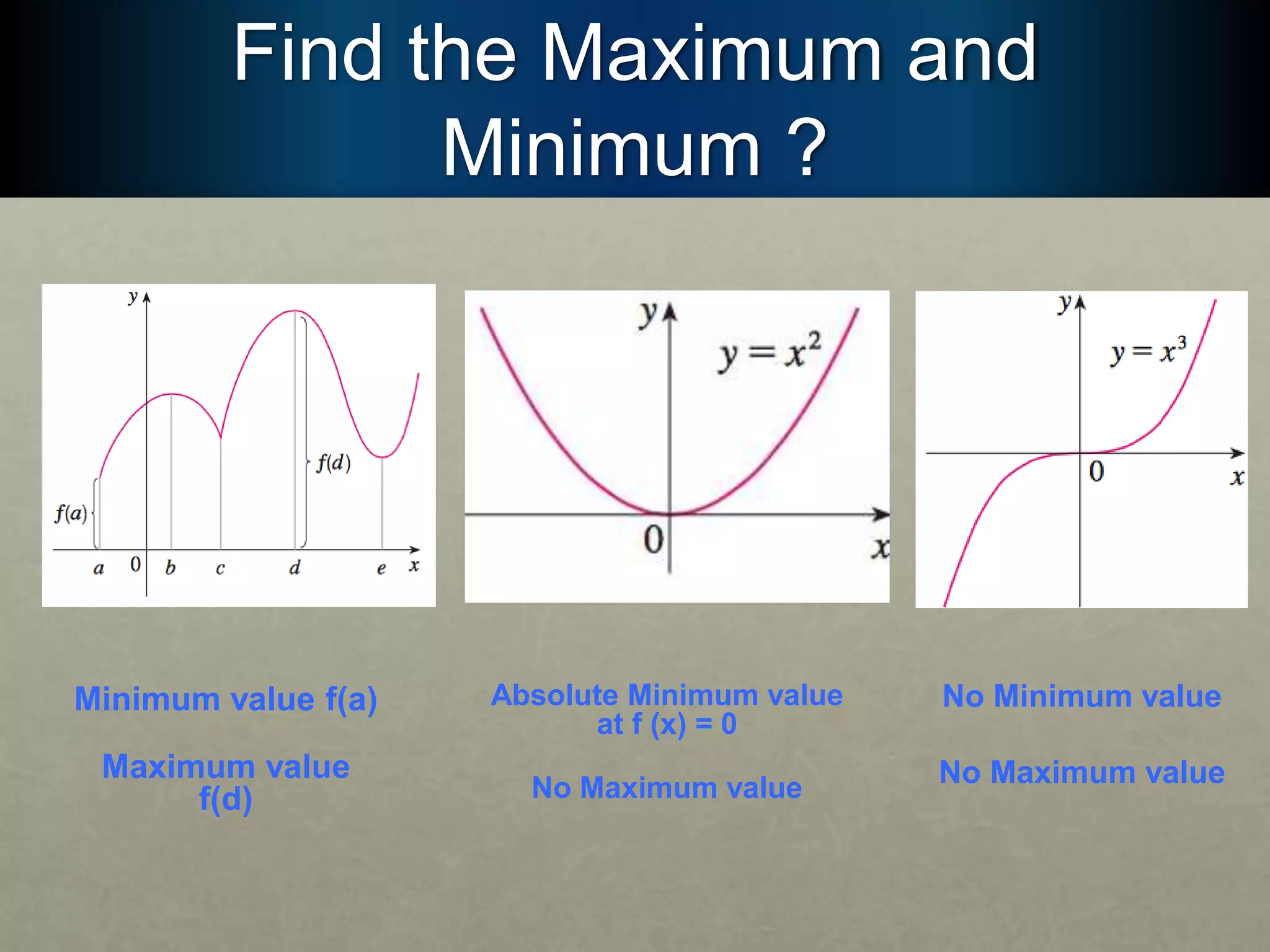
This document discusses the concepts of absolute and local maxima and minima in calculus, outlining their definitions and significance in optimization problems. It describes critical numbers, methods for finding extreme values, and includes tests for increasing/decreasing behavior as well as concavity. Additionally, it presents the second derivative test for identifying local extrema and inflection points.

1. Maximum & Minimum
Values
Calculus 1
Chapter 4.1 and 4.3
Ms. Medina

2. Why is this important?
• An important application of differential calculus are
problems dealing with optimization.
Examples:
• What is the shape of a can that minimizes manufacturing
cost?
• What is the maximum acceleration of a space
shuttle?
• What is the radius of a contracted windpipe that
expels air most rapidly during a cough?

3. Definition: Absolute Maximum &
Minimum
Absolute Maximum (global maximum)
A function f has an absolute maximum at c if f(􏰅c) ≥ 􏰅􏰅f(􏰅x)
􏰅for all x in D, where D is the domain of f. The number f(􏰅c) 􏰅
is called the maximum value of f on D.
Absolute Minimum (global minimum)
A function f has an absolute minimum at c if f(􏰅c)􏰅 ≤ 􏰅 f(􏰅x)
􏰅 for all x in D and the number f(􏰅c)􏰅 is called the minimum
value of f on D.
The maximum and minimum values of f are called the extreme
values of f.

4. Find the Maximum and
Minimum ?
Minimum value f(a)
Maximum value
f(d)
Absolute Minimum value
at f (x) = 0
No Maximum value
No Minimum value
No Maximum value

5. Definition: Local Maximum &
Minimum
Local Maximum (relative maximum)
A function f has a local maximum at c if f􏰮(c)􏰮 ≥􏰮 f(􏰮
x)􏰮 when x is near c. [This means that f(􏰮c)􏰮 ≥􏰮 f􏰮
(x)􏰮 for all x in some open interval containing c.]
Local Minimum (relative minimum)
Similarly, f has a local minimum at c if f(􏰮c)􏰮 ≤􏰮 f(􏰮
x)􏰮 when x is near c.

6. Definition: Critical numbers
Critical Numbers
• A critical number of a function f is a number c in the
domain of f such that either f`’(c)􏰯 =􏰯 0 or f’(c)􏰯
does not exist.
• If f has a local maximum or minimum at c, then c is a
critical number of f.

7. Closed Interval Method
Finding the absolute maximum and minimum values of a
continuous function f on a closed interval 􏰮a, b􏰮:
1. Find the values of f at the critical numbers of f in 􏰮a, b
􏰮.
2. Find the values of f at the endpoints of the interval.
3. The largest of the values from Steps 1 and 2 is the
absolute maximum value; the smallest of these values
is the absolute minimum value.

8. Increasing & Decreasing
Test
Increasing
If f’(􏰮􏰮x) > 0 on an interval,
then f is increasing on that
interval.
Decreasing
If f’(􏰮x)􏰮 <􏰮 0 on an
interval, then f is decreasing
on that interval.

9. The First Derivative Test
• Suppose that c is a critical number of
a continuous function f.
• If f’􏰮 changes from positive to
negative at c, then f has a local
maximum at c.
• If f’􏰮 changes from negative to
positive at c, then f has a local
minimum at c.
• If f’ does not change sign at c, then f
has no local maximum or minimum at
c.
• Example:
If f’ is positive on both sides of c or
negative on both sides
Direction Critical
Point
Direction
+ c -
- c +
- c -
+ c +

10. Definition: Concave up & Down
Concave Up
• If the graph of f lies above
all of its tangents on an
interval I, then it is called
concave upward on I.
Concave Down
• If the graph of f lies below
all of its tangents on I, it is
called concave downward
on I.

11. Concavity Test
• If f”(x) > 􏰮􏰮0 for all x in I,
then the graph of f is
concave upward on I.
• If f”(x) < 􏰮􏰮0 for all x in I,
then the graph of f is
concave downward on I.

12. Definition: Inflection Points
• A point P on a curve y = f(􏰮
x)􏰮 is called an inflection
point if f is continuous
there and the curve
changes from
• concave upward to
concave down- ward
• concave downward to
concave upward
at P.

13. The Second Derivative Test
• Suppose f’’ is continuous near c.
• If f’(c)􏰮 =􏰮 0 and f’’(c)􏰮􏰮 > 0,then f has a local minimum
at c.
• If f’(c) = 􏰮􏰮0and f”(c) < 0,then f has a local maximum at c.
Example of Second Derivative Test

14. Reference
• Stewart, J., Calculus Early Transcendental, sixth
edition. 2008.