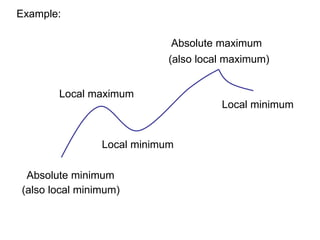
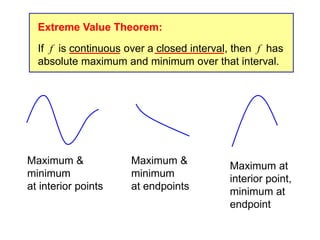
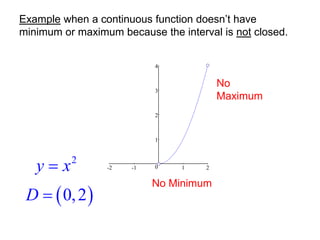
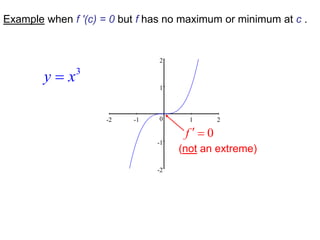
The document defines absolute and local maximum and minimum values of functions. An absolute (or global) maximum is the highest value a function can take over its entire domain, while an absolute minimum is the lowest value. A local maximum/minimum is the highest/lowest value a function takes in the neighborhood of a particular point. The Extreme Value Theorem states that continuous functions on closed intervals attain both absolute maximum and minimum values. Fermat's Theorem provides that local extrema occur where the derivative is 0 or undefined. To find absolute extrema, one evaluates the function at critical points and endpoints.

1. Maximum and Minimum
Values

2. Definition:
• A function f has an absolute maximum (or global
maximum) at c if f(c) ≥ f(x) for all x in D, where D
is the domain of f. The number f(c) is called
maximum value of f on D.
• Similarly, f has an absolute minimum at c if f(c) ≤
f(x) for all x in D and the number f(c) is called the
minimum value of f on D.
• The maximum and minimum values of f are called
the extreme values of f.
Absolute Maximum and Minimum

3. Definition:
• A function f has a local maximum (or
relative maximum) at c if f(c) ≥ f(x) when x
is near c.
• Similarly, f has a local minimum at c if f(c) ≤
f(x) when x is near c.
Local Maximum and Minimum

4. Absolute minimum
(also local minimum)
Local maximum
Local minimum
Absolute maximum
(also local maximum)
Local minimum
Example:

5. Extreme Value Theorem:
If f is continuous over a closed interval, then f has
absolute maximum and minimum over that interval.
Maximum &
minimum
at interior points
Maximum &
minimum
at endpoints
Maximum at
interior point,
minimum at
endpoint

6. 0
1
2
3
4
-2 -1 1 2
2
y x

 
0,2
D 
No Minimum
No
Maximum
Example when a continuous function doesn’t have
minimum or maximum because the interval is not closed.

7. Local maximum
Local minimum
Notice that local extremes in the interior of the function
occur where is zero or is undefined.
f  f 
Absolute maximum
(also local maximum)
Suppose we know that extreme values exist. How to find them?

8. Fermat’s Theorem
If f has a local maximum or minimum at
c, and if f ′(c) exists, then f ′(c) = 0 .
Note: When f ′(c) = 0 , f doesn’t necessarily have a
maximum or minimum at c. (In other words, the
converse of Fermat’s Theorem is false in general).

9. -2
-1
0
1
2
-2 -1 1 2
3
y x

0
f  
(not an extreme)
Example when f ′(c) = 0 but f has no maximum or minimum at c .

10. Critical numbers
• Definition: A critical number of a function f is a
number c in the domain of f such that either f ′(c) = 0
or f ′(c) doesn’t exist.
• Example: Find the critical numbers of f(x) = x1/2(x-3)
Solution:
Thus, the critical numbers are 0 and 1.
• If f has a local maximum or minimum at c , then c is a
critical number of f .
x
x
x
x
x
x
x
x
x
f
2
3
3
2
2
3
2
3
)
(










11. The closed interval method for finding
absolute maximum or minimum
To find the absolute maximum and minimum values
of a continuous function f on a closed interval
[a,b]:
1. Find the values of f at the critical numbers of f in
(a,b) .
2. Find the values of f at the endpoints of the
interval.
3. The largest of the values from Steps 1 and 2 is
the absolute maximum value; the smallest of
these values is the absolute minimum value.
Examples on the board.