Quadratic Functions Min Max
•
1 like•2,342 views
The maximum area for Betty's garden is 156.25 sq meters when each side is 12.5 meters long. This is found by modeling the problem with the equations: 2L + 2W = 50 MAX = LW Solving the equations gives L = W = 12.5 meters.
Report
Share
Report
Share
Download to read offline
Recommended
Solving Equations Involving Radical Expressions

This document discusses how to solve radical equations by isolating the radical expression, removing the radical sign by raising both sides to the appropriate power, and solving the resulting equation. It provides examples of solving various radical equations step-by-step and checking solutions. Key steps include isolating the radical term, removing the radical, solving the resulting equation, and checking for extraneous roots.
Solving linear inequalities

A linear inequality is similar to a linear equation but uses inequality symbols like < or > instead of =. A solution to a linear inequality is any coordinate pair that makes the inequality true. A linear inequality describes a half-plane region on a coordinate plane where all points in the region satisfy the inequality, with the boundary line given by the related equation. To graph a linear inequality, you solve it for y, graph the boundary line as solid or dotted, and shade the correct half-plane above or below the line.
Rational exponents and radicals 

Rational exponents are exponents that are ratios or fractions. There are three different ways to write a rational exponent: as a ratio of exponents, as a root of a root, and with a variable exponent. Rational exponents can be rewritten between exponential and radical forms. They follow the standard exponent rules when simplifying expressions, distributing exponents over division and applying negative exponent rules.
Factor Theorem and Remainder Theorem

Factor Theorem and Remainder Theorem. Mathematics10 Project under Mrs. Marissa De Ocampo. Prepared by Danielle Diva, Ronalie Mejos, Rafael Vallejos and Mark Lenon Dacir of 10- Einstein. CNSTHS.
Factor theorem

The document discusses the factor theorem and how to determine if a polynomial is a factor of another polynomial. It provides examples of using the factor theorem to show that (x + 1) is a factor of 2x^3 + 5x^2 - 3 and that (x - 2) is a factor of x^4 + x^3 - x^2 - x - 18. It also gives an example of finding a polynomial function given its zeros as -2, 1, -1. The document provides exercises for using the factor theorem to determine unknown values in polynomials.
3.8.1 Dilations and Scale Factor

The document defines and provides examples of dilations and scale factors. It explains that a dilation changes the size but not the shape of a figure. The scale factor is the ratio of the image to the preimage, where a scale factor greater than 1 enlarges the figure and less than 1 shrinks it. Examples are given of finding scale factors, determining new dimensions after a dilation, finding coordinates of dilated points and vertices, and dilating triangles and other figures centered at various points using different scale factors.
Solving radical equations

The document discusses solving radical equations. It introduces radical equations and explains that to solve them, one isolates the radical term, raises both sides of the equation to the equivalent index to eliminate the radical, solves the resulting equation, and checks the solution. It provides examples of solving various radical equations and checking the solutions. It also discusses using the Pythagorean theorem and solving problems involving areas of squares and lengths of sides and diagonals.
7.2 simplifying radicals

The document discusses simplifying radical expressions. It defines key terms like the radical sign and radicand. It provides two methods for simplifying radicals: using the product property to rewrite with the largest perfect square factor or making a factor tree to pull out factors. Examples are provided to demonstrate simplifying radicals of various forms, including those with variables and higher root expressions. The document also contains practice problems for simplifying radical expressions.
Recommended
Solving Equations Involving Radical Expressions

This document discusses how to solve radical equations by isolating the radical expression, removing the radical sign by raising both sides to the appropriate power, and solving the resulting equation. It provides examples of solving various radical equations step-by-step and checking solutions. Key steps include isolating the radical term, removing the radical, solving the resulting equation, and checking for extraneous roots.
Solving linear inequalities

A linear inequality is similar to a linear equation but uses inequality symbols like < or > instead of =. A solution to a linear inequality is any coordinate pair that makes the inequality true. A linear inequality describes a half-plane region on a coordinate plane where all points in the region satisfy the inequality, with the boundary line given by the related equation. To graph a linear inequality, you solve it for y, graph the boundary line as solid or dotted, and shade the correct half-plane above or below the line.
Rational exponents and radicals 

Rational exponents are exponents that are ratios or fractions. There are three different ways to write a rational exponent: as a ratio of exponents, as a root of a root, and with a variable exponent. Rational exponents can be rewritten between exponential and radical forms. They follow the standard exponent rules when simplifying expressions, distributing exponents over division and applying negative exponent rules.
Factor Theorem and Remainder Theorem

Factor Theorem and Remainder Theorem. Mathematics10 Project under Mrs. Marissa De Ocampo. Prepared by Danielle Diva, Ronalie Mejos, Rafael Vallejos and Mark Lenon Dacir of 10- Einstein. CNSTHS.
Factor theorem

The document discusses the factor theorem and how to determine if a polynomial is a factor of another polynomial. It provides examples of using the factor theorem to show that (x + 1) is a factor of 2x^3 + 5x^2 - 3 and that (x - 2) is a factor of x^4 + x^3 - x^2 - x - 18. It also gives an example of finding a polynomial function given its zeros as -2, 1, -1. The document provides exercises for using the factor theorem to determine unknown values in polynomials.
3.8.1 Dilations and Scale Factor

The document defines and provides examples of dilations and scale factors. It explains that a dilation changes the size but not the shape of a figure. The scale factor is the ratio of the image to the preimage, where a scale factor greater than 1 enlarges the figure and less than 1 shrinks it. Examples are given of finding scale factors, determining new dimensions after a dilation, finding coordinates of dilated points and vertices, and dilating triangles and other figures centered at various points using different scale factors.
Solving radical equations

The document discusses solving radical equations. It introduces radical equations and explains that to solve them, one isolates the radical term, raises both sides of the equation to the equivalent index to eliminate the radical, solves the resulting equation, and checks the solution. It provides examples of solving various radical equations and checking the solutions. It also discusses using the Pythagorean theorem and solving problems involving areas of squares and lengths of sides and diagonals.
7.2 simplifying radicals

The document discusses simplifying radical expressions. It defines key terms like the radical sign and radicand. It provides two methods for simplifying radicals: using the product property to rewrite with the largest perfect square factor or making a factor tree to pull out factors. Examples are provided to demonstrate simplifying radicals of various forms, including those with variables and higher root expressions. The document also contains practice problems for simplifying radical expressions.
7.7 Solving Radical Equations

This document provides steps for solving radical equations:
1) Isolate the radical on one side of the equation by performing inverse operations
2) Raise both sides of the equation to a power equal to the index of the radical to eliminate the radical
3) Solve the remaining polynomial equation
It includes examples of solving simpler radical equations as well as more complex equations involving fractions and multiple radicals. Checking solutions is emphasized as extraneous solutions may occasionally occur. Graphing calculators can also help visualize and find solutions to radical equations.
Mathematics 9 Lesson 3: Quadratic Functions

This powerpoint presentation discusses or talks about the topic or lesson Functions. It also discusses and explains the rules, steps and examples of Quadratic Functions.
Multiplying Monomials

1. The document discusses multiplying and simplifying monomial expressions. It defines monomials and explains the rules for multiplying them, including adding exponents when multiplying like terms and multiplying all exponents when an expression is raised to a power.
2. The document also discusses multiplying monomials and polynomials using the distributive property and applying the same exponent rules. It provides examples of multiplying and simplifying expressions involving monomials and polynomials.
3. The learning objectives are to multiply monomials, simplify expressions with monomials, and to multiply a monomial and a polynomial.
Solving quadratics by completing the square

The document discusses solving quadratic equations by completing the square. It provides examples of perfect square trinomials and how to find the missing constant term to create them. The steps for solving a quadratic equation by completing the square are described: 1) move all terms to the left side, 2) find and add the "completing the square" term, 3) factor into a perfect square trinomial, 4) take the square root of each side, 5) solve the resulting equations. Additional examples demonstrate applying these steps to solve quadratic equations algebraically.
Polynomial Function and Synthetic Division

This presentation explains the basic information about Polynomial Function and Synthetic Division. Examples were given about easy ways to divide polynomial function using synthetic division. It also contains the steps on how to perform the division method of polynomial functions.
Completing the square

This document provides examples and instructions for solving quadratic equations by completing the square. It begins with examples of solving quadratic equations using the square root property. It then explains how to complete the square to write a quadratic expression as a perfect square trinomial. Examples are provided to demonstrate completing the square and using it to solve quadratic equations. The document ensures readers understand completing the square through check examples and objectives.
Zero and Negative Exponents

- The document discusses how computers use negative exponents to process fractions and percentages during photo processing, which allows apps like Photoshop to shrink photos.
- It explains that negative exponents represent fractions, with the item with the negative exponent moving to the denominator when written as a fraction. This allows computers to perform mathematical operations involving fractions.
- Examples are provided of how negative exponents simplify to fractions through the rule of a-m = 1/am, with the item in the exponent moving between the numerator and denominator.
Graphing quadratic equations

1) This document discusses how to solve quadratic equations by graphing, including identifying the terms of a quadratic equation, finding the solutions by graphing, and graphing quadratic functions.
2) The key steps for graphing a quadratic function are to find the axis of symmetry using the standard form equation, find the vertex point, and find two other points to reflect across the axis of symmetry to complete the parabolic graph.
3) An example problem walks through graphing the quadratic equation y = x^2 - 4x by first finding the roots, vertex, and axis of symmetry, and then constructing a table to plot points and graph the parabola.
11.3 slope of a line

This document discusses finding the slope of a line from two points or an equation. It provides the slope formula and explains how to calculate slope given two points on a line. It also discusses horizontal and vertical lines, which have slopes of 0 and undefined, respectively. The document shows how to find the slope of a line from its equation by solving for y and taking the coefficient of x. It concludes by explaining how to determine if two lines are parallel, perpendicular, or neither based on the equality or product of their slopes. Examples are provided to demonstrate these concepts.
Adding and subtracting radical expressions

The document discusses operations on radicals, including simplifying radicals by identifying the index and radicand, and adding or subtracting radical expressions by combining like terms that have the same index and radicand. It provides examples of simplifying expressions involving addition and subtraction of radicals, emphasizing that unlike indices cannot be combined.
Rewriting Linear Equation from standard form to slope intercept form

This SIM was crafted to address the needs of learners with difficulty in rewriting linear equation from standard form into slope intercept form
Quadratic functions

The document discusses quadratic functions and their graphs. It defines quadratic functions as functions of the form f(x)=ax^2+bx+c, where a is not equal to 0. The graph of a quadratic function is a parabola with certain characteristics: it is symmetrical about an axis of symmetry and has a vertex which is either a maximum or minimum point. The axis of symmetry is the line x=0 for functions of the form f(x)=ax^2 and the vertex is at (0,0). For functions of the form f(x)=ax^2+k, the graph is a translation of f(x)=ax^2, so the vertex is (0,k) and the
Graphing Quadratics

This document provides information about graphing quadratic functions. It defines the standard form of a quadratic function as y = ax^2 + bx + c and explains that the sign of a determines if the parabola opens up or down. It describes how to find the axis of symmetry, vertex, domain and range. The steps to graph a quadratic function are given as finding the axis of symmetry, the vertex, and then two other points to reflect across the axis and connect with a smooth curve. Methods for finding the axis of symmetry, vertex, y-intercept and solutions are demonstrated through examples.
3.3 Zeros of Polynomial Functions

This document discusses key concepts related to finding zeros of polynomial functions including:
1) The factor theorem, which states that a polynomial x - k is a factor of a function f(x) if and only if f(k) = 0.
2) The rational zeros theorem, which gives possible rational zeros based on the factors of the leading coefficient and constant term.
3) The fundamental theorem of algebra, which states that every polynomial of degree n has n complex zeros and examples of finding functions based on given zeros.
4) The conjugate zeros theorem, which states that if z = a + bi is a zero, then z = a - bi is also a zero for polynomials with real coefficients.
5
Solving Quadratic Equations

Provides example on how to solve quadratic equations using extracting square roots, factoring, completing the square and quadratic formula.
Simplifying Rational Expression

This document discusses manipulations of rational expressions. It begins by differentiating between rational numbers and rational expressions. The objectives are to simplify, multiply, divide, add and subtract rational expressions. Examples are provided to distinguish rational numbers from expressions. Steps are outlined for simplifying expressions, including factorizing and cancelling common factors. Students work through practice problems in groups and individually. The document concludes by assigning further study on multiplying and dividing rational expressions.
Slope of a Line

This document contains a lesson on slope of a line from a mathematics course. It includes examples of calculating slope given two points on a line, identifying whether graphs represent constant or variable rates of change, and word problems applying slope to real-world contexts like cost of fruit and gas. The key points are that slope is defined as the ratio of rise over run, or change in y over change in x, and represents the constant rate of change for linear equations and functions.
Chapter 5 Slopes of Parallel and Perpendicular Lines

This document provides a lesson on identifying and writing equations for parallel and perpendicular lines. It includes examples of identifying parallel lines based on their having the same slope. Perpendicular lines are defined as having slopes whose product is -1. The document also demonstrates how to write equations for lines parallel or perpendicular to a given line based on their point and slope. Examples are provided to illustrate finding slopes from graphs and using them to determine if lines are parallel or perpendicular.
Quadratic functions my maths presentation

1. The document discusses key concepts related to quadratic equations including factorizing, solving, graphing, finding roots and axis of symmetry, locating maximum/minimum values, and using graphs to solve related equations and inequalities.
2. The key steps provided to factorize a quadratic equation are to find the product and factors of the coefficients that add up to the middle term, and then pair the factors.
3. To solve a quadratic equation, take all terms to one side, factorize, set each factor equal to 0 and solve for x to find the two roots.
Solve Systems By Elimination

1) Put the equations in standard form if needed
2) Determine that y can be eliminated by multiplying the top equation by 3
3) Multiply the top equation by 3 and add it to the bottom equation to eliminate y
4) Solve the resulting equation for the remaining variable
5) Substitute back into one of the original equations to find the other variable
The solution to the system is (1, -2).
Lesson 18: Maximum and Minimum Values (Section 041 slides)

There are various reasons why we would want to find the extreme (maximum and minimum values) of a function. Fermat's Theorem tells us we can find local extreme points by looking at critical points. This process is known as the Closed Interval Method.
Lesson 18: Maximum and Minimum Values (handout)

There are various reasons why we would want to find the extreme (maximum and minimum values) of a function. Fermat's Theorem tells us we can find local extreme points by looking at critical points. This process is known as the Closed Interval Method.
More Related Content
What's hot
7.7 Solving Radical Equations

This document provides steps for solving radical equations:
1) Isolate the radical on one side of the equation by performing inverse operations
2) Raise both sides of the equation to a power equal to the index of the radical to eliminate the radical
3) Solve the remaining polynomial equation
It includes examples of solving simpler radical equations as well as more complex equations involving fractions and multiple radicals. Checking solutions is emphasized as extraneous solutions may occasionally occur. Graphing calculators can also help visualize and find solutions to radical equations.
Mathematics 9 Lesson 3: Quadratic Functions

This powerpoint presentation discusses or talks about the topic or lesson Functions. It also discusses and explains the rules, steps and examples of Quadratic Functions.
Multiplying Monomials

1. The document discusses multiplying and simplifying monomial expressions. It defines monomials and explains the rules for multiplying them, including adding exponents when multiplying like terms and multiplying all exponents when an expression is raised to a power.
2. The document also discusses multiplying monomials and polynomials using the distributive property and applying the same exponent rules. It provides examples of multiplying and simplifying expressions involving monomials and polynomials.
3. The learning objectives are to multiply monomials, simplify expressions with monomials, and to multiply a monomial and a polynomial.
Solving quadratics by completing the square

The document discusses solving quadratic equations by completing the square. It provides examples of perfect square trinomials and how to find the missing constant term to create them. The steps for solving a quadratic equation by completing the square are described: 1) move all terms to the left side, 2) find and add the "completing the square" term, 3) factor into a perfect square trinomial, 4) take the square root of each side, 5) solve the resulting equations. Additional examples demonstrate applying these steps to solve quadratic equations algebraically.
Polynomial Function and Synthetic Division

This presentation explains the basic information about Polynomial Function and Synthetic Division. Examples were given about easy ways to divide polynomial function using synthetic division. It also contains the steps on how to perform the division method of polynomial functions.
Completing the square

This document provides examples and instructions for solving quadratic equations by completing the square. It begins with examples of solving quadratic equations using the square root property. It then explains how to complete the square to write a quadratic expression as a perfect square trinomial. Examples are provided to demonstrate completing the square and using it to solve quadratic equations. The document ensures readers understand completing the square through check examples and objectives.
Zero and Negative Exponents

- The document discusses how computers use negative exponents to process fractions and percentages during photo processing, which allows apps like Photoshop to shrink photos.
- It explains that negative exponents represent fractions, with the item with the negative exponent moving to the denominator when written as a fraction. This allows computers to perform mathematical operations involving fractions.
- Examples are provided of how negative exponents simplify to fractions through the rule of a-m = 1/am, with the item in the exponent moving between the numerator and denominator.
Graphing quadratic equations

1) This document discusses how to solve quadratic equations by graphing, including identifying the terms of a quadratic equation, finding the solutions by graphing, and graphing quadratic functions.
2) The key steps for graphing a quadratic function are to find the axis of symmetry using the standard form equation, find the vertex point, and find two other points to reflect across the axis of symmetry to complete the parabolic graph.
3) An example problem walks through graphing the quadratic equation y = x^2 - 4x by first finding the roots, vertex, and axis of symmetry, and then constructing a table to plot points and graph the parabola.
11.3 slope of a line

This document discusses finding the slope of a line from two points or an equation. It provides the slope formula and explains how to calculate slope given two points on a line. It also discusses horizontal and vertical lines, which have slopes of 0 and undefined, respectively. The document shows how to find the slope of a line from its equation by solving for y and taking the coefficient of x. It concludes by explaining how to determine if two lines are parallel, perpendicular, or neither based on the equality or product of their slopes. Examples are provided to demonstrate these concepts.
Adding and subtracting radical expressions

The document discusses operations on radicals, including simplifying radicals by identifying the index and radicand, and adding or subtracting radical expressions by combining like terms that have the same index and radicand. It provides examples of simplifying expressions involving addition and subtraction of radicals, emphasizing that unlike indices cannot be combined.
Rewriting Linear Equation from standard form to slope intercept form

This SIM was crafted to address the needs of learners with difficulty in rewriting linear equation from standard form into slope intercept form
Quadratic functions

The document discusses quadratic functions and their graphs. It defines quadratic functions as functions of the form f(x)=ax^2+bx+c, where a is not equal to 0. The graph of a quadratic function is a parabola with certain characteristics: it is symmetrical about an axis of symmetry and has a vertex which is either a maximum or minimum point. The axis of symmetry is the line x=0 for functions of the form f(x)=ax^2 and the vertex is at (0,0). For functions of the form f(x)=ax^2+k, the graph is a translation of f(x)=ax^2, so the vertex is (0,k) and the
Graphing Quadratics

This document provides information about graphing quadratic functions. It defines the standard form of a quadratic function as y = ax^2 + bx + c and explains that the sign of a determines if the parabola opens up or down. It describes how to find the axis of symmetry, vertex, domain and range. The steps to graph a quadratic function are given as finding the axis of symmetry, the vertex, and then two other points to reflect across the axis and connect with a smooth curve. Methods for finding the axis of symmetry, vertex, y-intercept and solutions are demonstrated through examples.
3.3 Zeros of Polynomial Functions

This document discusses key concepts related to finding zeros of polynomial functions including:
1) The factor theorem, which states that a polynomial x - k is a factor of a function f(x) if and only if f(k) = 0.
2) The rational zeros theorem, which gives possible rational zeros based on the factors of the leading coefficient and constant term.
3) The fundamental theorem of algebra, which states that every polynomial of degree n has n complex zeros and examples of finding functions based on given zeros.
4) The conjugate zeros theorem, which states that if z = a + bi is a zero, then z = a - bi is also a zero for polynomials with real coefficients.
5
Solving Quadratic Equations

Provides example on how to solve quadratic equations using extracting square roots, factoring, completing the square and quadratic formula.
Simplifying Rational Expression

This document discusses manipulations of rational expressions. It begins by differentiating between rational numbers and rational expressions. The objectives are to simplify, multiply, divide, add and subtract rational expressions. Examples are provided to distinguish rational numbers from expressions. Steps are outlined for simplifying expressions, including factorizing and cancelling common factors. Students work through practice problems in groups and individually. The document concludes by assigning further study on multiplying and dividing rational expressions.
Slope of a Line

This document contains a lesson on slope of a line from a mathematics course. It includes examples of calculating slope given two points on a line, identifying whether graphs represent constant or variable rates of change, and word problems applying slope to real-world contexts like cost of fruit and gas. The key points are that slope is defined as the ratio of rise over run, or change in y over change in x, and represents the constant rate of change for linear equations and functions.
Chapter 5 Slopes of Parallel and Perpendicular Lines

This document provides a lesson on identifying and writing equations for parallel and perpendicular lines. It includes examples of identifying parallel lines based on their having the same slope. Perpendicular lines are defined as having slopes whose product is -1. The document also demonstrates how to write equations for lines parallel or perpendicular to a given line based on their point and slope. Examples are provided to illustrate finding slopes from graphs and using them to determine if lines are parallel or perpendicular.
Quadratic functions my maths presentation

1. The document discusses key concepts related to quadratic equations including factorizing, solving, graphing, finding roots and axis of symmetry, locating maximum/minimum values, and using graphs to solve related equations and inequalities.
2. The key steps provided to factorize a quadratic equation are to find the product and factors of the coefficients that add up to the middle term, and then pair the factors.
3. To solve a quadratic equation, take all terms to one side, factorize, set each factor equal to 0 and solve for x to find the two roots.
Solve Systems By Elimination

1) Put the equations in standard form if needed
2) Determine that y can be eliminated by multiplying the top equation by 3
3) Multiply the top equation by 3 and add it to the bottom equation to eliminate y
4) Solve the resulting equation for the remaining variable
5) Substitute back into one of the original equations to find the other variable
The solution to the system is (1, -2).
What's hot (20)
Rewriting Linear Equation from standard form to slope intercept form

Rewriting Linear Equation from standard form to slope intercept form
Chapter 5 Slopes of Parallel and Perpendicular Lines

Chapter 5 Slopes of Parallel and Perpendicular Lines
Viewers also liked
Lesson 18: Maximum and Minimum Values (Section 041 slides)

There are various reasons why we would want to find the extreme (maximum and minimum values) of a function. Fermat's Theorem tells us we can find local extreme points by looking at critical points. This process is known as the Closed Interval Method.
Lesson 18: Maximum and Minimum Values (handout)

There are various reasons why we would want to find the extreme (maximum and minimum values) of a function. Fermat's Theorem tells us we can find local extreme points by looking at critical points. This process is known as the Closed Interval Method.
March 19 Trig With 2 Triangles

This document contains information about two triangles used to solve for the length of line BD. Triangle ABC has angles of 30, 42, and 50 degrees and triangle ACD has angles of 35, 56, and 36 degrees. The problem is asking to use the information provided to calculate the length of line CD.
March 19 Trig Review

Trigonometry is used to determine the measures (sides and angles) of a right triangle. The document reviews three trigonometric functions: sine, cosine, and tangent. Sine relates an angle to the opposite side over the hypotenuse. Cosine relates an angle to the adjacent side over the hypotenuse. Tangent relates an angle to the opposite side over the adjacent side. An example problem is shown to find missing sides and angles of a right triangle when given one angle measure and the side opposite to it.
Lesson 19: Maximum and Minimum Values

The closed interval method tells us how to find the extreme values of a continuous function defined on a closed, bounded interval: we check the end points and the critical points.
Maximums and minimum 

Applications of maximums and minimums in Calculus. This includes infection points, critical points, increasing and decreasing, etc.
March 19 Quadratic Test Review

The function is a quadratic function in the form f(x) = ax2 + bx + c, with a = 2, b = -4, and c = -1. It has a vertex of (1, -3), an axis of symmetry at x = 1, a domain of all real numbers, and a range of [-3,∞). The y-intercept is -1 and the x-intercepts (roots) are 1 ± 0.5√6.
Viewers also liked (7)
Lesson 18: Maximum and Minimum Values (Section 041 slides)

Lesson 18: Maximum and Minimum Values (Section 041 slides)
Similar to Quadratic Functions Min Max
35182797 additional-mathematics-form-4-and-5-notes

1) The function f(x) = 2x^2 + 8x + 6 can be written as f(x) = 2(x+2)^2 - 2. The maximum point is (-2, -2) and the equation of the tangent at this point is y = -2.
2) The function f(x) = -(x-4)^2 + h has a maximum point at (k, 9) so k = 4 and h = 9.
3) The function y = (x+m)^2 + n has an axis of symmetry at x = -m. Given the axis is x = 1, m = -1 and the minimum point is (1
Modul 3 quadratic function

This document provides information about quadratic functions including:
1) The general form of a quadratic function is f(x) = ax2 + bx + c, where a, b, c are constants and a ≠ 0.
2) Characteristics of quadratic functions include involving one variable only and the highest power of the variable being 2.
3) Examples are provided to demonstrate recognizing quadratic and non-quadratic functions based on their form.
Functions limits and continuity

This document discusses functions, limits, and continuity. It begins by defining functions, domains, ranges, and some standard real functions like constant, identity, modulus, and greatest integer functions. It then covers limits of functions including one-sided limits and properties of limits. Examples are provided to illustrate evaluating limits using substitution and factorization methods. The overall objectives are to understand functions, domains, ranges, limits of functions and methods to evaluate limits.
Gr 11 equations

Quadratic equations can be solved in several ways:
1) Factorizing, by finding two numbers whose product is the constant term and sum is the coefficient of the x term.
2) Using the quadratic formula.
3) Substitution, by letting an expression like x^2 + 2x equal a variable k, and solving the simplified equation for k and back substituting.
4) Squaring both sides, but this can introduce extraneous solutions so one must check solutions.
Quadratic Expressions

The same function can have different functional expressions in different ranges. Finding maximum/minimum values in these cases becomes very interesting
Class XII CBSE Mathematics Sample question paper with solution

Class XII CBSE Mathematics Sample question paper with solutionPratima Nayak ,Kendriya Vidyalaya Sangathan
The document is a sample question paper for Class XII Mathematics. It consists of 3 sections - Section A has 10 one-mark questions, Section B has 12 four-mark questions, and Section C has 7 six-mark questions. All questions are compulsory. The paper tests concepts related to matrices, trigonometry, calculus, differential equations, and vectors. Internal choices are provided in some questions. Calculators are not permitted.functions limits and continuity

This document provides an overview of functions, limits, and continuity. It defines key concepts such as domain and range of functions, and examples of standard real functions. It also covers even and odd functions, and how to calculate limits, including left and right hand limits. Methods for evaluating algebraic limits using substitution, factorization, and rationalization are presented. The objectives are to understand functions, domains, ranges, and how to evaluate limits of functions.
3c. Pedagogy of Mathematics (Part II) - Algebra (Ex 3.3)

Pedagogy of Mathematics (Part II) - Algebra, Algebra, Maths, IX std Maths, Samacheerkalvi maths, II year B.Ed., Pedagogy, Mathematics, Polynomials, Constants, variables, algebraic
Feb 22. Exercise 6

The maximum area of the rectangular pen is 800 square metres when its width is 20 metres and length is 40 metres. The minimum sum of the squares of two positive numbers whose sum is 13 is 84.5, which occurs when the numbers are 6.5. The projectile reaches its maximum height of 326 metres after 8 seconds. The greatest revenue from theatre admission occurs at a price of $0.90 per ticket. The maximum product of two positive numbers whose sum is 13 is 42.25, which occurs when both numbers are 6.5.
Feb 23 Extra Min Max Problems

The maximum area of the fenced enclosure is 300 sqm when the width of each pen is 10m and the overall length is 30m.
The maximum daily profit of $19,600 for the amusement park is achieved when the admission price is increased to $14.
The maximum area of the triangle is 21.125 sqcm when the height is 6.5cm, which makes the base also 6.5cm.
Integrales 

This document contains a table listing 85 integrals and their solutions. Each integral is expressed in terms of common trigonometric, exponential, logarithmic and hyperbolic functions. The solutions are provided in closed form with many involving combinations of elementary functions.
HARMONIC OSCILLATION FOR BTECH 1ST YEAR

1) The harmonic oscillator model describes an object oscillating back and forth around an equilibrium position due to a restoring force proportional to its displacement.
2) In quantum mechanics, the harmonic oscillator leads to discrete, quantized energy levels equally spaced by an amount of energy hν, where ν is the oscillator frequency. The lowest energy level is not zero due to the uncertainty principle.
3) The wavefunctions and energies of the quantum harmonic oscillator are obtained by solving the Schrödinger equation, which yields the Hermite differential equation. The solutions are Hermite polynomials multiplied by a Gaussian function.
Transforming Quadratic functions from General Form to Standard Form

The document describes how to transform quadratic functions from general form to standard form in 3 steps:
1) Factor out the leading coefficient a from the first two terms
2) Complete the square of the second term
3) Factor and combine the terms into standard form (f(x) = a(x - h)2 + k)
It provides examples of applying this process to functions like f(x) = x2 - 8x + 3 and f(x) = 2x2 + 5x - 1. Finally, it lists 5 quadratic functions and directs the reader to transform them into standard form.
Ch02s

This document contains solutions to various circuit analysis problems. Problem 2.1 solves for the output voltage of a voltage divider circuit given input and resistor values. Problem 2.2 analyzes a circuit with a diode and calculates the output voltage as a function of the input voltage and diode characteristics. The remaining problems continue analyzing circuits involving resistors, diodes, capacitors and calculating values such as output voltage, current, power dissipation and more. Equations are provided and used to solve for unknown variables in each circuit.
Zeros of polynomial functions

This document provides examples and explanations of factoring polynomials and finding zeros of polynomial functions. It covers factoring polynomials using the difference of squares, sum and difference of cubes, and perfect squares and cubes. It also shows how to find all zeros of polynomial functions by factoring them into linear and quadratic factors and setting each factor equal to zero.
Quadratic equation by four different methods

1. The document provides examples of solving quadratic equations using different methods.
2. Various word problems involving quadratic equations are presented, such as finding unknown lengths, areas, and numbers that satisfy given conditions.
3. The examples are solved step-by-step showing the calculations and reasoning involved in arriving at the solutions.
Calculus1.key

This document presents a new method for solving the classic box-folding problem of determining the largest box that can be made by cutting squares from the corners of a sheet of paper and connecting the edges. The traditional method is described along with its history. A new volume equation is then derived that accounts for additional volume gained by folding the cut-off squares. For a sheet that is a square, this new method provides a 10% larger box volume than the classic approach.
Sample question paper 2 with solution

This document provides a sample question paper for Class XII Mathematics. It consists of 3 sections - Section A has 10 one-mark questions, Section B has 12 four-mark questions, and Section C has 7 six-mark questions. The paper is for 3 hours and carries a total of 100 marks. Some questions provide internal choices. Calculators are not permitted. Sample questions include finding inverse functions, evaluating integrals, solving differential equations, and probability questions.
MA8353 TPDE

1. The document provides 14 problems involving partial differential equations (PDEs). The problems involve forming PDEs by eliminating arbitrary constants from functions, finding complete integrals, and solving PDEs.
2. Methods used include taking partial derivatives, finding auxiliary equations, and making substitutions to isolate the PDE or solve it.
3. The document covers a range of techniques for working with PDEs, including eliminating constants, finding trial solutions, integrating subsidiary equations, and solving auxiliary equations to find complete integrals.
Completing the square

1) The document discusses completing the square, which involves rewriting quadratic expressions in the form (x + a)2 + b to find maximum and minimum values.
2) Examples are provided of completing the square for expressions like x2 + 8x + 3 and 2x2 + 4x + 11.
3) The technique of setting the expression equal to 0 and solving for x is described as a way to find the minimum value and the corresponding x-value that produces it.
Similar to Quadratic Functions Min Max (20)
35182797 additional-mathematics-form-4-and-5-notes

35182797 additional-mathematics-form-4-and-5-notes
Class XII CBSE Mathematics Sample question paper with solution

Class XII CBSE Mathematics Sample question paper with solution
3c. Pedagogy of Mathematics (Part II) - Algebra (Ex 3.3)

3c. Pedagogy of Mathematics (Part II) - Algebra (Ex 3.3)
Transforming Quadratic functions from General Form to Standard Form

Transforming Quadratic functions from General Form to Standard Form
More from ste ve
March 17 Chequebook Recod

You start with $400 in your chequing account. On March 18 you deposit a $300 paycheck, bringing your balance to $700. On March 19 you write 4 cheques: cheque #22 for $45 to Manitoba Hydro, cheque #23 for $55 to the City of Winnipeg, cheque #24 for $200 to Visa, and cheque #25 for $50 to DMCI, reducing your balance to $350.
March 18 Reconciliation

Reconciling a bank statement involves comparing transaction records to the bank's statement to identify any differences. When reconciling, the reconciler finds transactions recorded by one party but not the other. By accounting for these differences in a reconciliation statement, the reconciler can ensure the final balances match and identify any potential errors made by either party. The process involves listing matching transactions, recording the initial balances, then adding deposits or subtracting withdrawals found in one record but not the other to make the final balances equal. If the balances do not match after reconciliation, an error has occurred that requires correction.
March 18 Radicals

This document discusses square roots and their properties. It provides examples of taking the square root of both sides of an equation to solve for the variable. It also shows combining like terms within square root expressions and then taking the square root of both sides to isolate the variable.
March 18 Withdrawal Slips

Withdrawal slips are records of when and how much money is taken out of a bank account. The document instructs the reader to fill out a sample withdrawal slip pretending to withdraw $100 from their account on the current date. The slip would document the pretend $100 withdrawal for record keeping purposes.
March 18 Compound Interest

The document discusses compound interest rates across three scenarios. In the first, investing $1000 at 8% interest compounded semi-annually for 4 years would yield more than the original $1000. In the second, Jim's Bank offering 6% interest compounded monthly on deposits over $2000 is a better choice than Steve's Bank offering 5% compounded weekly, if the money is left for 2 years. In the third, Peter buys a $500 laptop on a credit card with 17.5% interest compounded monthly but cannot pay for 6 months, making the real cost of the laptop more than $500.
March 17 Rule Of 72

The document discusses the rule of 72, which is a method for estimating how long it will take an investment to double in value at a given annual interest rate. It states that to estimate the number of years for an investment to double, one should divide 72 by the annual interest rate percentage. However, the document provides no further explanation or context regarding the rule of 72.
March 16 Compound Interest 2

The document discusses compound interest rates and calculations. It asks how much money would be earned from investing $1000 at 8% interest compounded semi-annually over 4 years. It also asks which bank would earn more interest over 2 years, between one offering 6% interest compounded monthly on deposits over $2000, and another offering 5% interest compounded weekly on the same size deposits.
March 12 Forms Of Lines

There are three forms of lines: slope-intercept form (y=mx+b), standard form (ax+by+c=0), and neither of the above. Slope-intercept form provides the slope and y-intercept in a simple way. Standard form writes the line as a polynomial with everything on one side of the equation and x positive. Standard form can be found by converting slope-intercept form or by knowing two points that the line passes through.
March 12 Discriminant

The document discusses the discriminant of a quadratic equation and what the sign of the discriminant indicates about the number of roots. It provides an example quadratic equation of 4x^2 + 3x + 8 = 0. It then shows:
1) Calculating the discriminant of -119 which is negative, indicating there are no real roots.
2) A general explanation that a negative discriminant means no real roots, while a positive discriminant means there are two real roots.
3) When the discriminant is 0, there is exactly one real root.
March 11 Deposit Slips

This document provides instructions for completing deposit slips based on sample transactions. It describes that a deposit slip records money deposited into a bank account. It gives an example of Betty depositing two cheques for $30 and $40, as well as $40 in cash and $4 in coins. It also provides an example for Steve depositing three cheques for $35, $47, and $25.67 and taking $40 in cash from the deposit. The document aims to demonstrate how to fill out deposit slips.
March 9 Quadratic Formula

The quadratic formula provides a method to solve quadratic equations of the form ax^2 + bx + c = 0. It expresses the solutions for x in terms of the coefficients a, b, and c as x = (-b ± √(b^2 - 4ac))/2a. The document demonstrates applying the quadratic formula to solve the equation 7x^2 + 14x - 3 = 0, obtaining the two solutions x1 = 0.2 and x2 = -2.2.
March 9 Determing Equations

The document provides examples of determining the equation of a line given information about its slope and a point it passes through. It works through four examples, finding the equation of a line with slope 7 and y-intercept -4, slope -4/5 passing through (1,3), slope 2/3 passing through (8,1), and slope 1/9 passing through (-2,5). The examples demonstrate how to set up and solve systems of equations to determine the y-intercept and write the equation in y=mx+b form.
March 9 Determing Equations

The document provides examples of determining the equation of a line given information about its slope and a point it passes through. It works through four examples, finding the equation of a line with slope 7 and y-intercept -4, slope -4/5 passing through (1,3), slope 2/3 passing through (8,1), and slope 1/9 passing through (-2,5). The examples demonstrate how to set up and solve systems of equations to determine the y-intercept and write the equation in y=mx+b form.
March 9 Quadratic Formula

The quadratic formula provides a method to solve quadratic equations of the form ax^2 + bx + c = 0. It expresses the solutions for x in terms of the coefficients a, b, and c as x = (-b ± √(b^2 - 4ac))/2a. The document demonstrates applying the quadratic formula to solve the equation 7x^2 + 14x - 3 = 0, obtaining the two solutions x1 = 0.2 and x2 = -2.2.
March 9 Ex 12

This document appears to be an exercise labeled as number 12. No other context or details are provided about the nature or content of the exercise. The single word "Exercise 12" is the only information given in the document.
March 8 Compound Interest

The document explains compound interest using examples of borrowing $1000 at 8% interest for 1 year, and then not paying it back for additional years. It shows how the interest builds on itself each year, with the borrower paying interest on accumulated interest. A formula is provided to calculate the final amount for any principal, interest rate, number of compounding periods per year, and term of years. An example calculates the amount owed after 2 years at 6% interest compounded semi-annually.
Ambiguous Case1

The document discusses the sine and cosine laws for solving triangles. It provides examples of using these laws to calculate missing angles and sides of triangles when given certain information. However, one of the examples leads to two possible triangle solutions, showing that the information provided an ambiguous case with multiple valid options. The summary concludes that without more context, both triangle solutions are considered correct since the given information allows for more than one possibility.
March 4 Pay Raise

This document discusses pay raises and how to calculate new salaries after a percentage increase. It provides two examples: one where Joan received an 8% raise on her $1000 monthly salary, increasing it to $1080, and another where Steve's $45,000 annual salary was increased 15% to $51,750 after his raise. Percentage raises are commonly used to increase employee salaries over time based on a set percentage of their current pay.
March 8 Quadratic Equations

This document defines key terms related to quadratic equations such as monomial, binomial, trinomial, and polynomial. It explains that a quadratic equation is a polynomial of the form ax^2 + bx + c = 0, which can be graphed as a parabola. The roots or zeros of a quadratic equation are the values of x where the equation equals 0. As an example, it finds the roots of the quadratic equation x^2 + 5x + 6 = 0 to be -2 and -3.
March 8 Pay Raise 2

This document provides examples of calculating percentage pay raises based on starting salary and new salary amounts. It first shows an example of calculating an 8% raise on a $10 hourly wage. It then gives an example of determining the percentage increase for an employee who received a $60 weekly raise on a $500 weekly wage, which is a 12% raise. The final example shows calculating an 8.333% raise for an employee whose annual pay will increase from $60,000 to $65,000.
More from ste ve (20)
Quadratic Functions Min Max
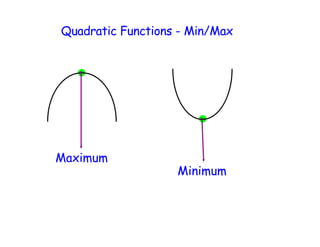
- 1. Quadratic Functions - Min/Max Maximum Minimum
- 2. What is the maximum value of the quadratic function: 2 y = -2(x + 4) - 9 (-4, -9) What is the minimum value of the quadratic function: 2 y = 3(x - 8) + 14 (8, 14)
- 3. Betty wants to make a rectangle shaped garden. She has 50 meters of fencing. What lengths of sides give Betty a garden with the maximum area? L W 2L + 2W = 50 MAX = LW
- 4. L 2L + 2W = 50 W MAX = LW L = 50 - 2W = 25 - W 2 MAX = (25 - W)W 2 MAX = -W + 25W
- 5. L 2L + 2W = 50 W MAX = LW 2 MAX = -W + 25W 2 MAX = -{W - 25W} 2 2 2 MAX = -{W - 25W + (25/2) - (25/2) } 2 2 MAX = -{(W - 25/2) - (25/2) }
- 6. L 2L + 2W = 50 W MAX = LW 2 2 MAX = -{(W - 25/2) - (25/2) } 2 MAX = -(W - 12.5) + 156.25
- 7. REMINDER: 2 y = a(x - p) + q The value of y is a maximum if a is - The value of y is a maximum when x = - p The value of y is a minimum if a is + The value of y is a minimum when x = -p
- 8. L 2L + 2W = 50 W MAX = LW 2 MAX = -(W - 12.5) + 156.25 - means a maximum does exist The maximum value will be the vertex, or when W = 12.5, it is 156.25.
- 9. L 2L + 2W = 50 W MAX = LW The maximum value will be the vertex, or when W = 12.5, it is 156.25. Can substitute these values back into the original equations to find the value of L 2L + 2(12.5) = 50 L = 50 - 25 = 12.5 2
- 10. We calculated that the maximum area that can be enclosed with 50 meters 2 of fence is 156.25 m . This area is possible when each side is 12.5m long. 12.5m 12.5m 2 12.5m 156.25m 12.5m
- 11. 304 people will go to a basketball game if the tickets cost 8 dollars. Every time the price is increase $0.50 16 fewer people will go to the game. What ticket price gives the maximum profits?
- 12. Profit = (Number of people)*(Cost per person) P=N*C x = number of times the price is increased P =N *C m m m Nm = N - 16x Cm = C + .5x Pm = (N - 16x) (C + .5x)
- 13. Pm = (N - 16x) (C + .5x) Pm = (304 - 16x) (8 + .5x) P = 2432 + 152x - 128x -8x2 m Pm = -8x2 + 24x + 2432
- 14. 2 + 24x + 2432 Pm = -8x 2 - 3x} Pm = -8{x + 2432 2 - 3x + 1.52 - 1.52} +2432 Pm = -8{x 2 2 Pm = -8{(x - 1.5) -1.5 } + 2432 Pm = -8(x-1.5) 2 + 18 + 2432
- 15. P = -8(x-1.5) 2 + 18 + 2432 m P = -8(x-1.5) 2 + 2450 m So, the max profit is when x = 1.5 x = number of times the price is increased Cm = C + .5x Cm = 8 + .5 (1.5) Cm = $8.75
- 16. ex. 6 1-5