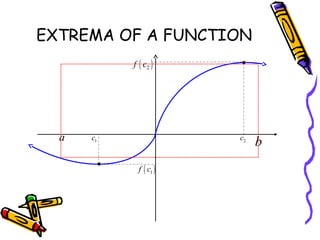
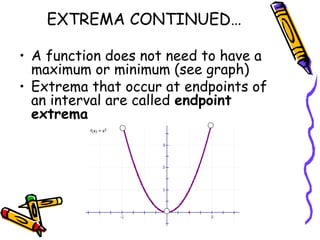
The document defines extrema as the extreme or maximum and minimum values of a function on an interval. An absolute extremum occurs at an endpoint of a closed interval, while a relative extremum occurs in the interior of an open interval. A function has extrema at points where the derivative is equal to 0 (critical points) or where the function is not differentiable. The Extreme Value Theorem states that a continuous function on a closed interval will have both an absolute maximum and minimum. To find the extrema of such a function, evaluate it at all critical points and endpoints. A function can have a maximum or minimum at multiple points within an interval.

1. EXTREMA ON AN
INTERVAL
Section 3.1

2. When you are done with your
homework, you should be able
to…
• Understand the definition of
extrema of a function on an interval
• Understand the definition of relative
extrema of a function on an open
interval
• Find extrema on a closed interval

3. EXTREMA OF A FUNCTION
f ( c2 )
a
c1
•
c2
•
f ( c1 )
b

4. DEFINITION OF EXTREMA
Let f be defined on an open interval I
containing c.
1. f ( c ) is the minimum of f on I if
f ( c) ≤ f ( x)
for all x in I.
f ( c)
f ( is) the (maximum of f on I if
c ≥ f c)
2.
for all x in I.

5. EXTREMA CONTINUED…
• The minimum and maximum of a
function on an interval are the
extreme values, or extrema of the
function on the interval
• The singular form of extrema is
extremum
• The minimum and maximum of a
function on an interval are also called
the absolute minimum and absolute
maximum on the interval

6. EXTREMA CONTINUED…
• A function does not need to have a
maximum or minimum (see graph)
• Extrema that occur at endpoints of
an interval are called endpoint
extrema
f (x) = x2
3
2
1
-2
2

7. THE EXTREME VALUE
THEOREM
If f is continuous on a closed interval
[ a, b] , then f has both a minimum
and a maximum on the interval.

8. DEFINITION OF RELATIVE
EXTREMA
1. If there is an open interval containing
c on which f ( c ) is a maximum, then f ( c )
is called a relative maximum of f, or
you can say that f has a relative
maximum at c, f ( c ) .
2. If there is an open interval containing
c on which f is a minimum, then f ( c ) is
called a relative minimum of f, or you
can say that f has a relative minimum
at c, f ( c ) .
(
(
)
)

9. Find the value of the
derivative (if it exists) at
the indicated extremum.
πx
f ( x ) = cos ; ( 2, −1)
2
0.0
0.0

10. Find the value of the
derivative (if it exists) at
the indicated extremum.
 2 2 3
r ( s ) = −3s s + 1;  − ,
 3 3 ÷
÷


0.0
0.0

11. Find the value of the
derivative (if it exists) at
the indicated extremum.
f ( x ) = 4 − x ; ( 0, 4 )

12. f ( x) − f ( c)
f ′ ( x ) = lim
x →c
x−c
f ( x ) − f ( 0)
( 4 − x ) − 4 =1
lim
= lim−
−
x →0
x →0
x−0
x
f ( x ) − f ( 0)
( 4 − x ) − 4 = −1
lim
= lim+
+
x →0
x →0
x−0
x
Therefore, f ′ ( 0 ) does not exist

13. DEFINITION OF A CRITICAL
NUMBER
Let f be defined at c.
1. If f ' ( c ) = 0, then c is a critical
number of f.
2. If f is not differentiable at c, then c
is a critical number of f.

14. Locate the critical
numbers of the
function.
A.
c = ±2
B. c = ±2, c = 0
C.
c = 2, c = 0
D. None of these
x +4
f ( x) =
x
2

15. Locate the critical numbers of the
function.
f ( θ ) = 2sec θ + tan θ , ( 0, 2π )
π
3π
7π
11π
, c=
, c=
A. c = , c =
2
2
6
6
7π
11π
B. c = 6 , c = 6
4π
5π
C. c = 3 , c = 3
D. None of these

16. THEOREM: RELATIVE EXTREMA
OCCUR ONLY AT CRITICAL
NUMBERS
If f has a relative maximum or minimum at
x=c
, then c is a critical number of
f.

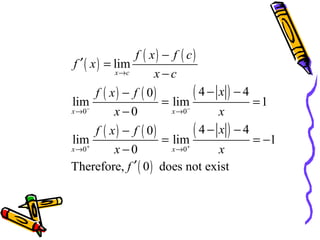
17. GUIDELINES FOR FINDING
EXTREMA ON A CLOSED
INTERVAL
To find the extrema of a continuous function
f on a closed interval [ a, b ] , use the
following steps.
1. Find the critical numbers of in .
2. Evaluate f at each critical number in ( a, b ).
3. Evaluate f at each endpoint of [ a, b] .
4. The least of these outputs is the
minimum. The greatest is the maximum.

18. The maximum of a function
that is continuous on a
closed interval at two
different values in the
interval.
A. True
B. False