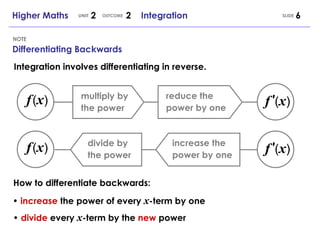
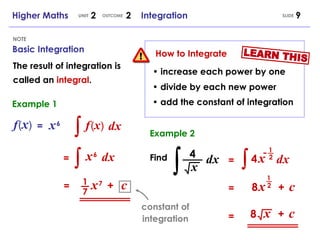
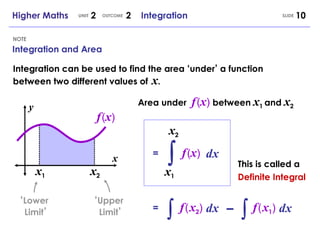
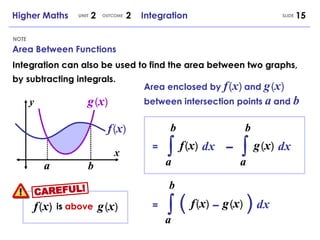
This document provides an overview of integration and how it relates to calculating areas under curves and between functions. Some key points covered include: - Integration uses the concept of reverse differentiation to calculate the area under a function. - The area under a function between two x-values a and b is calculated as the definite integral from a to b. - Integrals may be used to find the area between two curves by subtracting their integrals between the intersection points. 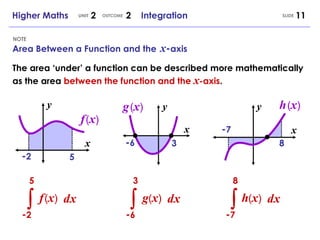- Integrals can represent either positive or negative areas depending on whether the area is above or below the x-axis.

1. Higher Maths 2 2 Integration UNIT OUTCOME SLIDE

2. Speed Time Graphs NOTE D S T × ÷ ÷ 20 40 0 0 2 4 Time (hours) Speed (mph) Calculate the distance travelled in each journey. 20 40 0 0 2 4 6 Time (hours) Speed (mph) 20 40 0 0 2 4 6 Time (hours) Speed (mph) D = 4 × 30 = 120 miles average speed D = 5 × 20 = 100 miles 30 miles 90 miles + 15 miles 135 miles In Speed Time graphs, the distance travelled is the same as the area under the graph . Higher Maths 2 2 Integration UNIT OUTCOME SLIDE

3. Reverse Differentiation NOTE D T speed = ‘ rate of change of distance with respect to time ’ REMEMBER If we know how the speed changes, and want to find distance, we need to ‘ undo ’ finding the rate of change with respect to time. In other words we need to reverse differentiate . Differentiating backwards is used to find the area under a function . f ( x ) Higher Maths 2 2 Integration UNIT OUTCOME SLIDE x y

4. Estimating Area Under Curves NOTE To estimate area under a function, split the area into vertical strips . f ( x ) x f ( x ) x The area of each strip is the height, multiplied by : x Total Area f ( x ) x ×  f ( x ) x × ( ) = As the strips get narrower , the estimate becomes more accurate. Area under the function  = f ( x ) f ( x ) x as 0  means ‘the sum of...’ Higher Maths 2 2 Integration UNIT OUTCOME SLIDE x x y x y

5. Higher Maths 2 2 Integration UNIT OUTCOME SLIDE Integration NOTE The algebraic method for finding area under a function is called Integration . ‘ Integrate’ means ‘join together all the pieces’ Integration uses reverse differentiation to ‘ undo ’ finding the rate of change. Area under the function  = f ( x ) f ( x ) x d x x as 0 f ( x ) = x d x Expression or function to be integrated. x y

6. Higher Maths 2 2 Integration UNIT OUTCOME SLIDE Differentiating Backwards NOTE Integration involves differentiating in reverse. multiply by the power reduce the power by one f ( x ) f ′ ( x ) divide by the power increase the power by one f ( x ) f ′ ( x ) • divide every x -term by the new power How to differentiate backwards: • increase the power of every x -term by one

7. Higher Maths 2 2 Integration UNIT OUTCOME SLIDE Finding the Anti-Derivative NOTE The result of a differentiation is called a derivative . • divide by each new power How to Reverse Differentiate • increase each power by one The result of differentiating backwards is called the anti-derivative . Example dy dx = 8 x 3 + x 2 – 6 x Find the anti-derivative for y y = dx 8 x 3 + x 2 – 6 x = 2 x 4 + x 3 – 3 x 2 1 3 d x expression or function

8. Higher Maths 2 2 Integration UNIT OUTCOME SLIDE The Constant of Integration NOTE When differentiating, part of an expression is often lost. Example f ( x ) = x 4 + 2 f ( x ) = x 4 f ( x ) = x 4 – 7 f ′ ( x ) = 4 x 3 All three functions have derivative The anti-derivative of f ′ ( x ) is f ( x ) = x 4 + c unknown constant When differentiating in reverse, it is essential to remember to add back on the unknown number. This is called the constant of integration .

9. Higher Maths 2 2 Integration UNIT OUTCOME SLIDE Basic Integration NOTE The result of integration is called an integral . f ( x ) Example 1 d x f ( x ) = x 6 • divide by each new power How to Integrate • increase each power by one = 1 7 = x 7 + c d x x 6 • add the constant of integration constant of integration Example 2 d x 4 x Find = d x 4 x 1 2 = 8 x + c = 8 x 1 2 + c LEARN THIS

10. Higher Maths 2 2 Integration UNIT OUTCOME SLIDE Integration and Area NOTE Integration can be used to find the area ‘ under ’ a function between two different values of x . f ( x ) x 1 x 2 d x f ( x ) x 1 x 2 = d x f ( x 2 ) – d x f ( x 1 ) Area under f ( x ) between x 1 and x 2 = ‘ Upper Limit ’ ‘ Lower Limit ’ This is called a Definite Integral x y

11. The area ‘under’ a function can be described more mathematically as the area between the function and the x -axis . Area Between a Function and the x - axis Higher Maths 2 2 Integration UNIT OUTCOME SLIDE NOTE x y f ( x ) d x f ( x ) 5 - 2 5 - 2 y g ( x ) d x g ( x ) 3 - 6 3 - 6 x y h ( x ) 8 - 7 x d x h ( x ) 8 - 7

12. Higher Maths 2 2 Integration UNIT OUTCOME SLIDE Evaluating Definite Integrals NOTE = dx 2 x 3 0 3 [ x 4 + c 1 2 ] 0 3 = ( × ( 3 ) 4 + c 1 2 ) ( × ( 0 ) 4 + c 1 2 ) – = 40 1 2 The constants of integration cancel each other out. Definite Integrals do not require the constant of integration. d x x 1 x 2 Definite Integral Write integral inside square brackets units 2 Example NOTICE

13. [ ] Higher Maths 2 2 Integration UNIT OUTCOME SLIDE Evaluating Definite Integrals (continued) NOTE Example 2 4 1 d x 4 1 9 x 2 – 2 x 3 x 3 – x 2 = ( ) 3 × 4 3 – 4 2 = – ( ) 3 × 1 3 – 1 2 ( ) 192 – 16 = – ( ) 3 – 1 = 174 units 2 Find the area below the curve between x = 1 and x = 4 . y = 9 x 2 – 2 x Write integral inside square brackets... (no constant required) ...then evaluate for each limit and subtract. Remember units!

14. When calculating areas by integration, areas above the x - axis are positive and areas below the x - axis are negative . Areas Above and Below the x - axis Higher Maths 2 2 Integration UNIT OUTCOME SLIDE NOTE x y b a c d dx f ( x ) a b > 0 dx f ( x ) c d < 0 f ( x ) How to calculate area between a curve and the • draw a sketch • calculate the areas above and below the axis separately • add the positive value of each area (ignore negative signs) x - axis : x -

15. Area Between Functions Integration can also be used to find the area between two graphs, by subtracting integrals. Higher Maths 2 2 Integration UNIT OUTCOME SLIDE NOTE f ( x ) x y g ( x ) Area enclosed by f ( x ) and g ( x ) d x f ( x ) = = – d x g ( x ) f ( x ) d x g ( x ) ( – ) b a b a b a b a between intersection points a and b is above f ( x ) g ( x ) CAREFUL!