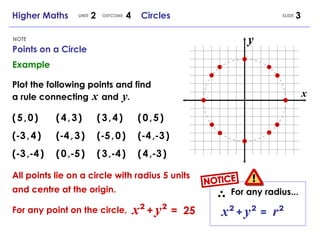
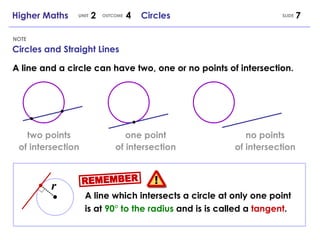
This document provides information about circles and their relationships to other geometric concepts: 1. It defines key concepts such as the distance formula, points on a circle, the equation of a circle with the center at the origin or other point (x,y), and the general equation of a circle. 2. It discusses the intersection of circles and lines, including finding the points of intersection using substitution and solving quadratics. The discriminant is used to determine the number of intersection points. 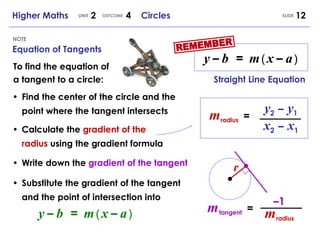3. Tangents are defined as lines that intersect a circle at only one point and formulas are given for finding the equation of a tangent line to a circle.

1. Higher Maths 2 4 Circles UNIT OUTCOME SLIDE

2. Distance Between Two Points NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME The Distance Formula d = ( y 2 – y 1 ) ² + ( x 2 – x 1 ) ² √ B ( x 2 , y 2 ) A ( x 1 , y 1 ) y 2 – y 1 x 2 – x 1 Example Calculate the distance between (-2,9) and (4,-3). d = + 6 ² √ 12 ² = 180 √ = 5 √ 6 Where required, write answers as a surd in its simplest form. REMEMBER

3. Points on a Circle NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME Example Plot the following points and find a rule connecting x and y . x y ( 5 , 0 ) ( 4 , 3 ) ( 3 , 4 ) ( 0 , 5 ) (-3 , 4 ) (-4 , 3 ) (-5 , 0 ) (-4 ,-3 ) (-3 ,-4 ) ( 0 ,-5 ) ( 3 ,-4 ) ( 4 ,-3 ) All points lie on a circle with radius 5 units and centre at the origin. x ² + y ² = 25 x ² + y ² = r ² For any point on the circle, For any radius... NOTICE

4. The Equation of a Circle with centre at the Origin NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME x ² + y ² = r ² For any circle with radius r and centre the origin, x y The ‘Origin’ is the point (0,0) origin Example Show that the point ( - 3 , ) lies on the circle with equation 7 x ² + y ² = 16 x ² + y ² = ( -3 ) ² + ( ) ² 7 = 9 + 7 = 16 Substitute point into equation: The point lies on the circle. LEARN THIS

5. The Equation of a Circle with centre ( a , b ) NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME ( x – a ) ² + ( y – b ) ² = r ² For any circle with radius r and centre at the point ( a , b ) ... Not all circles are centered at the origin. x y ( a , b ) r Example Write the equation of the circle with centre ( 3 , -5 ) and radius 2 3 . ( x – a ) ² + ( y – b ) ² = r ² ( x – 3 ) ² + ( y – ( -5 ) ) ² = ( ) ² 2 3 ( x – 3 ) ² + ( y + 5 ) ² = 12 LEARN THIS

6. NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME The General Equation of a Circle ( x + g ) 2 + ( y + f ) 2 = r 2 ( x 2 + 2 g x + g 2 ) + ( y 2 + 2 fy + f 2 ) = r 2 x 2 + y 2 + 2 g x + 2 f y + g 2 + f 2 – r 2 = 0 x 2 + y 2 + 2 g x + 2 f y + c = 0 c = g 2 + f 2 – r 2 r 2 = g 2 + f 2 – c r = g 2 + f 2 – c Try expanding the equation of a circle with centre ( - g , - f ) . General Equation of a Circle with center ( - g , - f ) and radius r = g 2 + f 2 – c this is just a number... LEARN

7. NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME Circles and Straight Lines A line and a circle can have two, one or no points of intersection. r A line which intersects a circle at only one point is at 90° to the radius and is is called a tangent . two points of intersection one point of intersection no points of intersection REMEMBER

8. NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME Intersection of a Line and a Circle Example Find the intersection of the circle and the line 2 x – y = 0 x 2 + ( 2 x ) 2 = 45 x 2 + 4 x 2 = 45 5 x 2 = 45 x 2 = 9 x = 3 or -3 y = 2 x x 2 + y 2 = 45 Substitute into y = 2 x : How to find the points of intersection between a line and a circle: • rearrange the equation of the line into the form y = m x + c • substitute y = m x + c into the equation of the circle • solve the quadratic for x and substitute into m x + c to find y y = 6 or -6 Points of intersection are ( 3,6 ) and ( -3,-6 ) .

9. NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME Intersection of a Line and a Circle (continued) Example 2 Find where the line 2 x – y + 8 = 0 intersects the circle x 2 + y 2 + 4 x + 2 y – 20 = 0 x y x 2 + ( 2 x + 8 ) 2 + 4 x + 2 ( 2 x + 8 ) – 20 = 0 x 2 + 4 x 2 + 32 x + 64 + 4 x + 4 x + 16 – 20 = 0 5 x 2 + 40 x + 60 = 0 5 ( x 2 + 8 x + 12 ) = 0 5 ( x + 2 )( x + 6 ) = 0 x = -2 or -6 Substituting into y = 2 x + 8 points of intersection as ( -2,4 ) and ( -6,-4 ) . Factorise and solve

10. NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME The Discriminant and Tangents x = - b b 2 – ( 4 ac ) ± 2 a b 2 – ( 4 ac ) Discriminant The discriminant can be used to show that a line is a tangent: • substitute into the circle equation • rearrange to form a quadratic equation • evaluate the discriminant y = m x + c b 2 – ( 4 ac ) > 0 Two points of intersection b 2 – ( 4 ac ) = 0 The line is a tangent b 2 – ( 4 ac ) < 0 No points of intersection r REMEMBER

11. NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME Circles and Tangents Show that the line 3 x + y = -10 is a tangent to the circle x 2 + y 2 – 8 x + 4 y – 20 = 0 Example x 2 + (- 3 x – 10 ) 2 – 8 x + 4 (- 3 x – 10 ) – 20 = 0 x 2 + 9 x 2 + 60 x + 100 – 8 x – 12 x – 40 – 20 = 0 10 x 2 + 40 x + 40 = 0 b 2 – ( 4 ac ) = 40 2 – ( 4 × 10 × 40 ) = 0 = 1600 – 1600 The line is a tangent to the circle since b 2 – ( 4 ac ) = 0 x y

12. NOTE SLIDE Higher Maths 2 4 Circles UNIT OUTCOME Equation of Tangents To find the equation of a tangent to a circle: • Find the center of the circle and the point where the tangent intersects • Calculate the gradient of the radius using the gradient formula • Write down the gradient of the tangent • Substitute the gradient of the tangent and the point of intersection into y – b = m ( x – a ) REMEMBER Straight Line Equation y – b = m ( x – a ) m tangent = – 1 m radius x 2 – x 1 y 2 – y 1 m radius = r