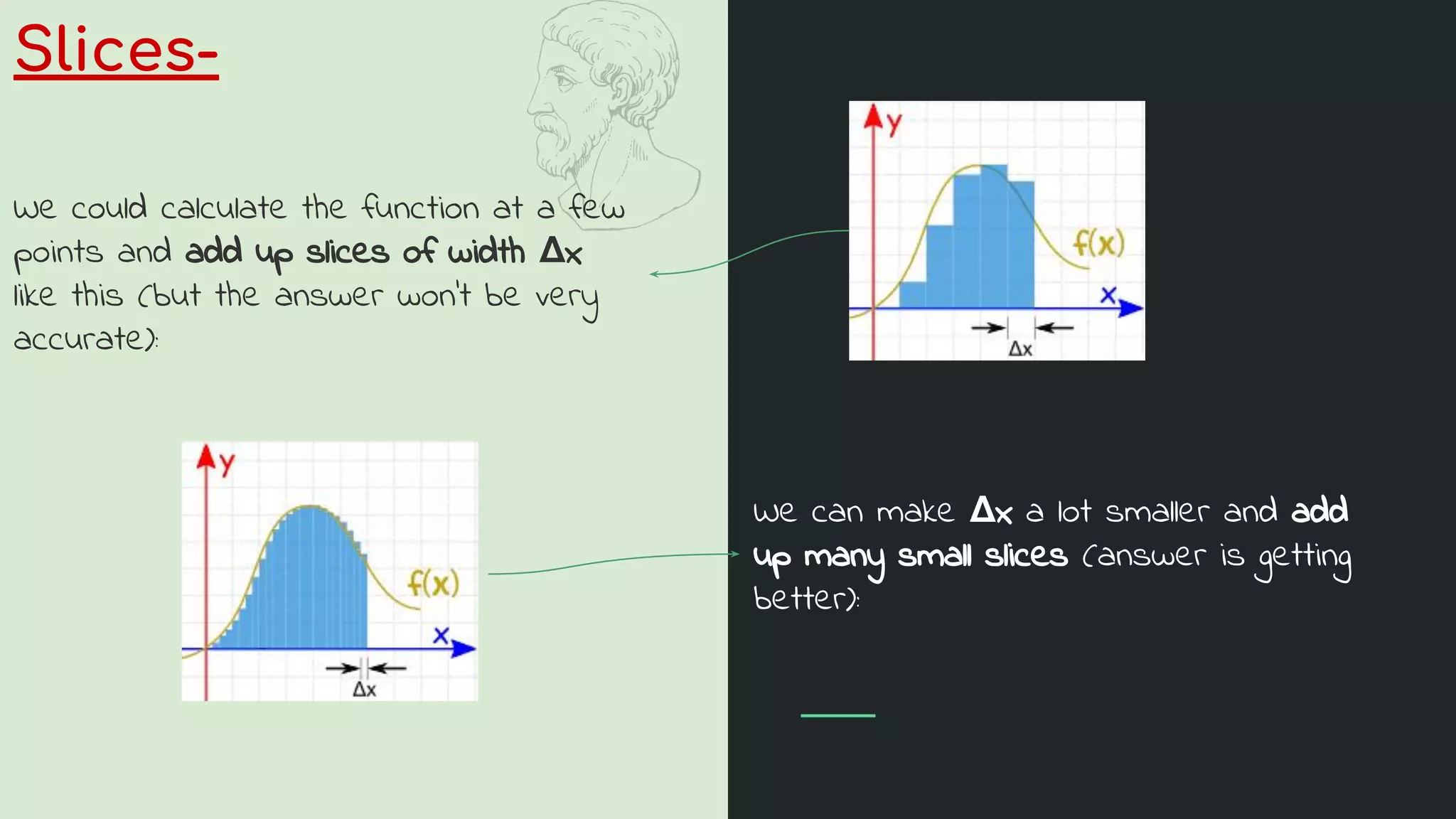
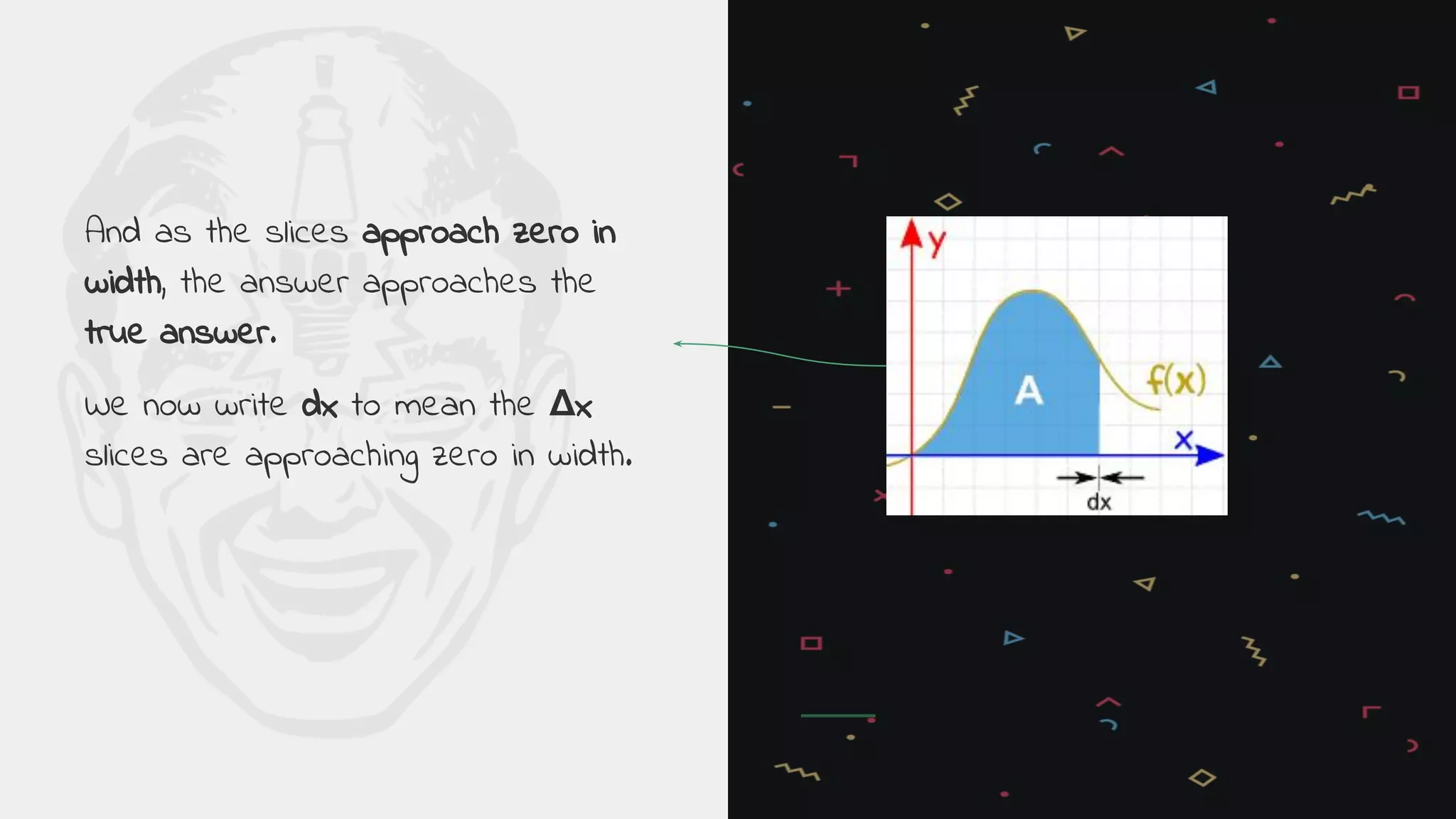
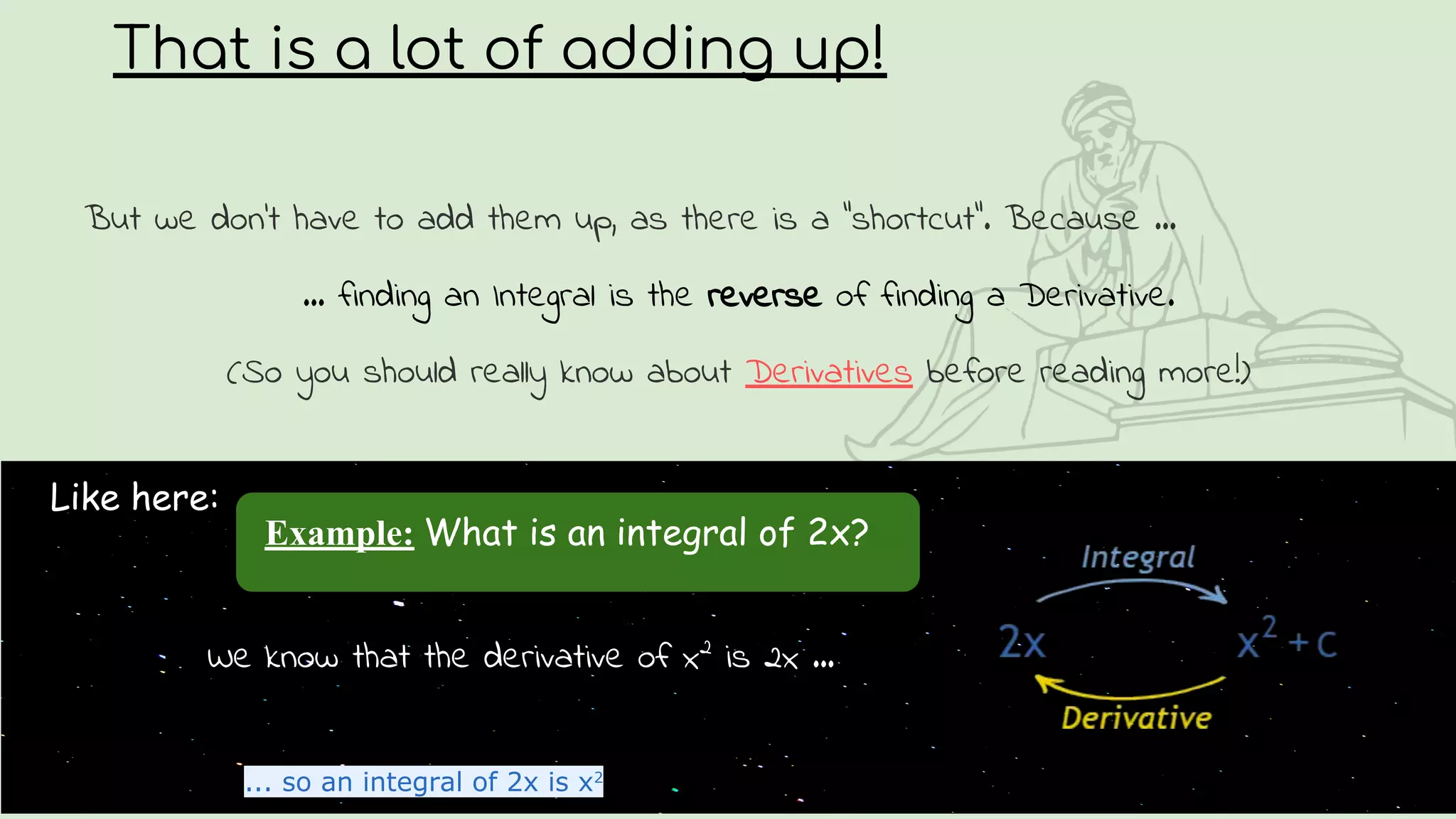
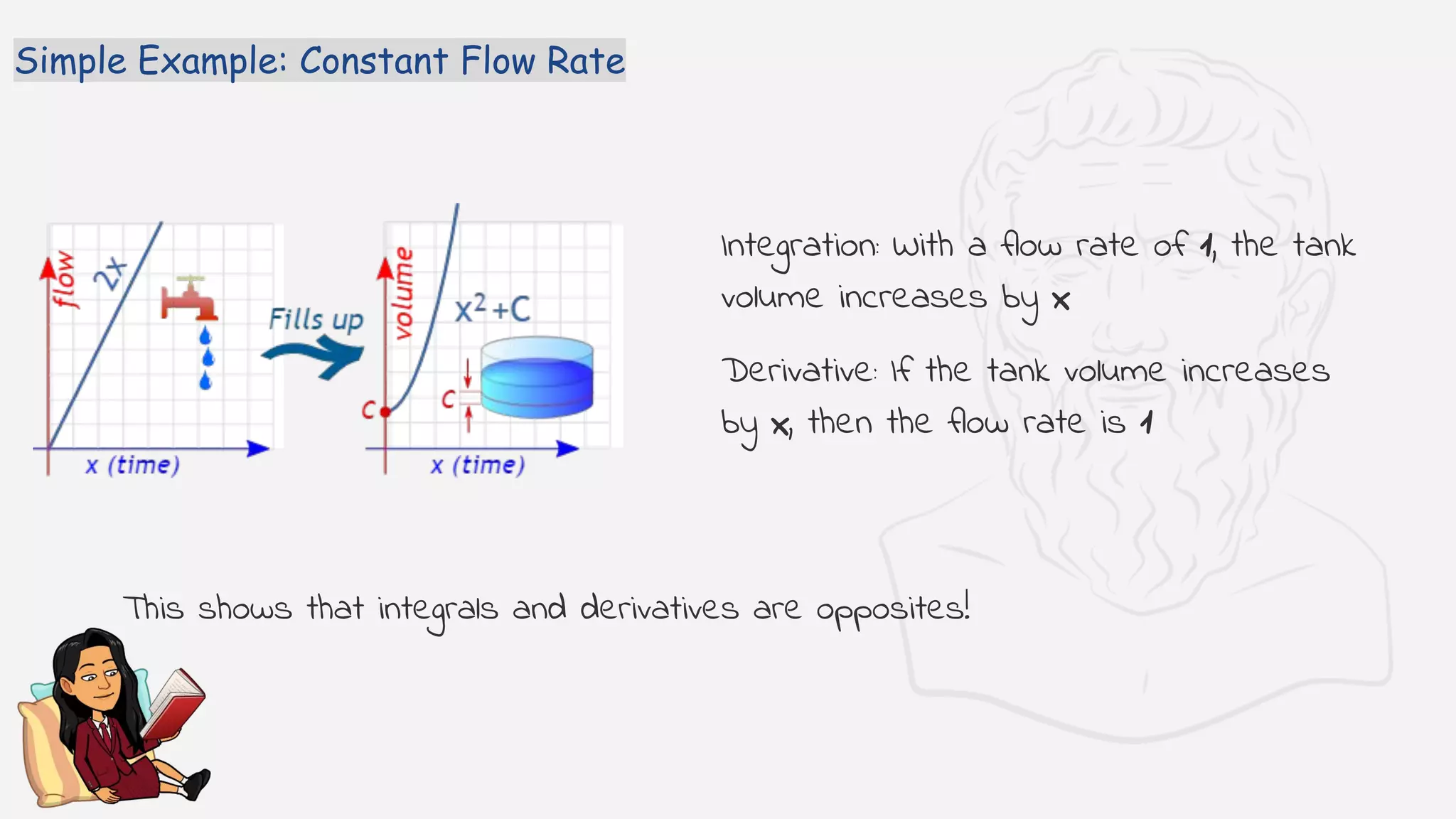
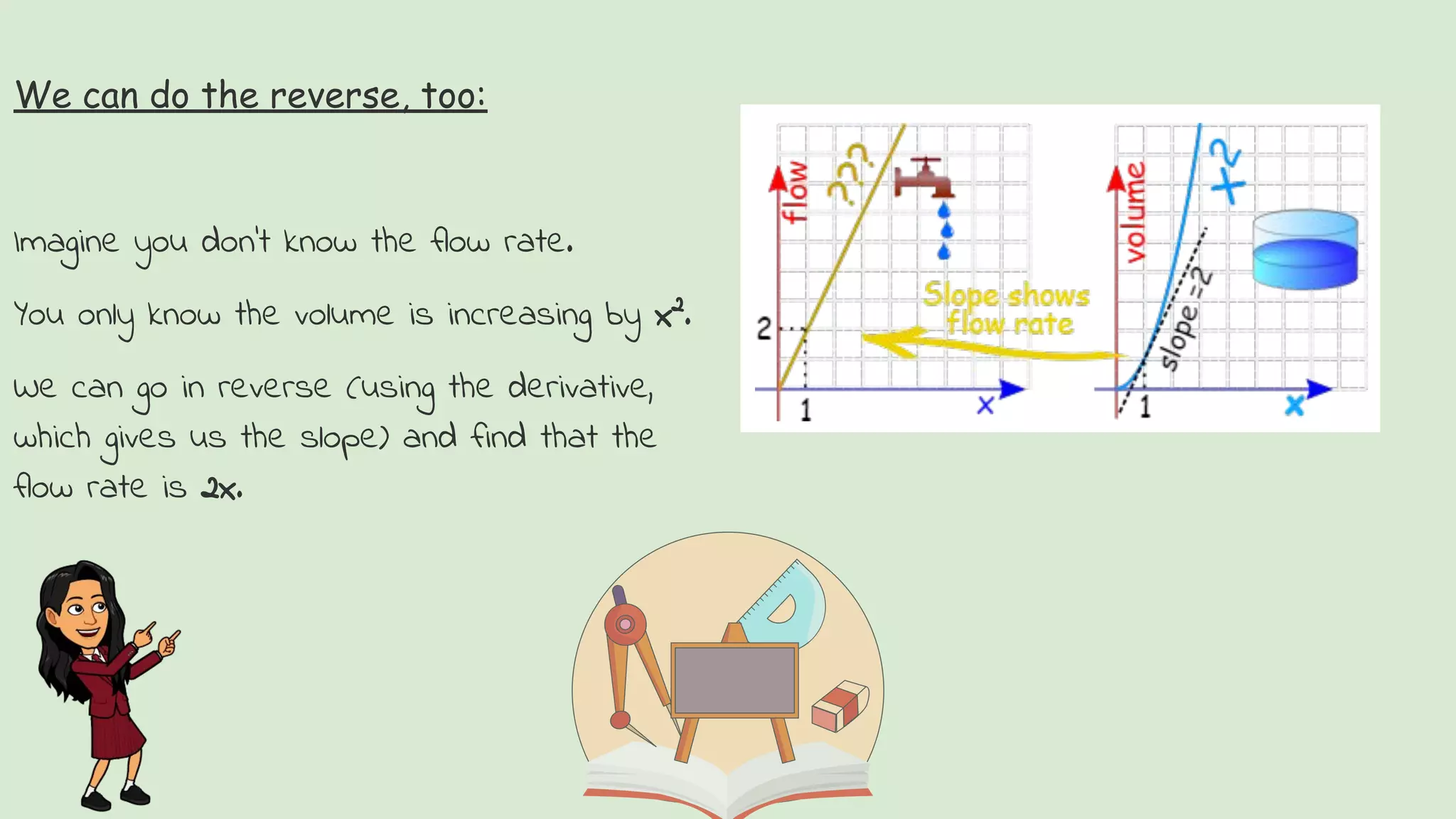
The document provides an introduction to integration. It explains that integration is the reverse of differentiation and can be used to find areas, volumes, and other quantities. It discusses how integration works by dividing a curve into infinitesimally thin slices and adding them up. The key concepts of the integral sign, the integrand, and the constant of integration are introduced. Applications of integration in physics, chemistry, medicine, and other fields are briefly outlined.

1. Abhay Pandey
Nehal Trisholiya

2. INTEGRATION
An equation for me has no meaning unless it expresses a
thought of GOD. -Srinivasa Ramanujan

3. Introduction to Integration
Integration is a way of adding slices to find the whole.
Integration can be used to find areas, volumes, central points and
many useful things. But it is easiest to start with finding the area
under the curve of a function like this
What is the area under y = f(x) ?

4. Slices-
We could calculate the function at a few
points and add up slices of width Δx
like this (but the answer won't be very
accurate):
We can make Δx a lot smaller and add
up many small slices (answer is getting
better):

5. And as the slices approach zero in
width, the answer approaches the
true answer.
We now write dx to mean the Δx
slices are approaching zero in width.

6. That is a lot of adding up!
But we don't have to add them up, as there is a "shortcut". Because ...
... finding an Integral is the reverse of finding a Derivative.
(So you should really know about Derivatives before reading more!)
Like here:
Example: What is an integral of 2x?
We know that the derivative of x2
is 2x ...
... so an integral of 2x is x2

7. Notation-
The symbol for "Integral" is a stylish "S"
(for "Sum", the idea of summing slices):
After the Integral Symbol we put the function we want to find the integral of
(called the Integrand),
and then finish with dx to mean the slices go in the x direction (and approach
zero in width).
And here is how we write the answer:

8. Plus C-
We wrote the answer as x2
but why + C ?
It is the "Constant of Integration". It is there because of all the functions
whose derivative is 2x:
The derivative of x2
+4 is 2x, and the derivative of x2
+99 is also 2x, and so on! Because the
derivative of a constant is zero.
So when we reverse the operation (to find the integral) we only know 2x, but there could have
been a constant of any value.
So we wrap up the idea by just writing + C at the end.

9. Tap and Tank-
Integration is like filling a tank from a tap.
The input (before integration) is the flow rate
from the tap.
Integrating the flow (adding up all the little bits
of water) gives us the volume of water in the
tank

10. Integration: With a flow rate of 1, the tank
volume increases by x
Derivative: If the tank volume increases
by x, then the flow rate is 1
Simple Example: Constant Flow Rate
This shows that integrals and derivatives are opposites!

11. Example: with the flow in liters per minute, and the tank
starting at 0
After 3 minutes (x=3):
● the flow rate has reached 2x = 2×3 = 6 liters/min,
● and the volume has reached x2
= 32
= 9 liters
And after 4 minutes (x=4):
● the flow rate has reached 2x = 2×4 = 8 liters/min,
● and the volume has reached x2
= 42
= 16 liters

12. We can do the reverse, too:
Imagine you don't know the flow rate.
You only know the volume is increasing by x2
.
We can go in reverse (using the derivative,
which gives us the slope) and find that the
flow rate is 2x.

13. Example:
● At 1 minute the volume is increasing at 2 liters/minute (the slope of
the volume is 2)
● At 2 minutes the volume is increasing at 4 liters/minute (the slope of
the volume is 4)
● At 3 minutes the volume is increasing at 6 liters/minute (a slope of 6)
● etc

14. So Integral and Derivative are opposites.
We can write that down this way:
The integral of the flow rate 2x tells us the volume of water::
And the slope of the volume increase x2
+C gives us back the flow rate:
∫2x dx = x2
+ C
(x2
+ C) = 2x

15. Applications of Integration
Application in Physics-
● To calculate the center of mass, center of gravity and mass moment of inertia of
vehicles, satellites, a tower and basically every other building or structure which you
can imagine.
● To calculate the velocity and trajectory of a satellite while placing it an orbit like at
exactly which point you need to give how much thrust to get the desired trajectory.
Application in Chemistry-
● To determine the rate of a chemical reaction and to determine some necessary
information of Radioactive decay reaction.

16. Application in Medical Science-
● To study the spread of infectious disease — relies heavily on
calculus. It can be used to determine how far and fast a disease
is spreading, where it may have originated from and how to best
treat it.

17. There are various other examples also like in global mapping. I can go on and
on but I think that I made it very clear that integration which is a part of
calculus is essential part of daily life and happening everyday, every-time
around us. Sometimes we notice it, we do not.
1. Applications of the Indefinite Integral
shows how to find displacement (from velocity) and velocity (from
acceleration) using the indefinite integral. There are also some electronics
applications in this section.
In primary school, we learned how to find areas of shapes with straight sides
(e.g. area of a triangle or rectangle). But how do you find areas when the
sides are curved? We'll find out how in:
2. Area Under a Curve and 3. Area Between 2 Curves

18. 4. Volume of Solid of Revolution- explains how to use integration to find
the volume of an object with curved sides, e.g. wine barrels.
5. Centroid of an Area- means the centre of mass. We see how to use
integration to find the centroid of an area with curved sides.
6. Moments of Inertia- explains how to find the resistance of a rotating
body. We use integration when the shape has curved sides.
7. Work by a Variable Force- shows how to find the work done on an object
when the force is not constant. This section includes Hooke's Law for
springs.
8. Electric Charges- have a force between them that varies depending on
the amount of charge and the distance between the charges. We use
integration to calculate the work done when charges are separated.

19. 9. Average Value- of a curve can be calculated using integration.
Head Injury Criterion is an application of average value and used in road
safety research.
10. Force by Liquid Pressure- varies depending on the shape of the object
and its depth. We use integration to find the force.