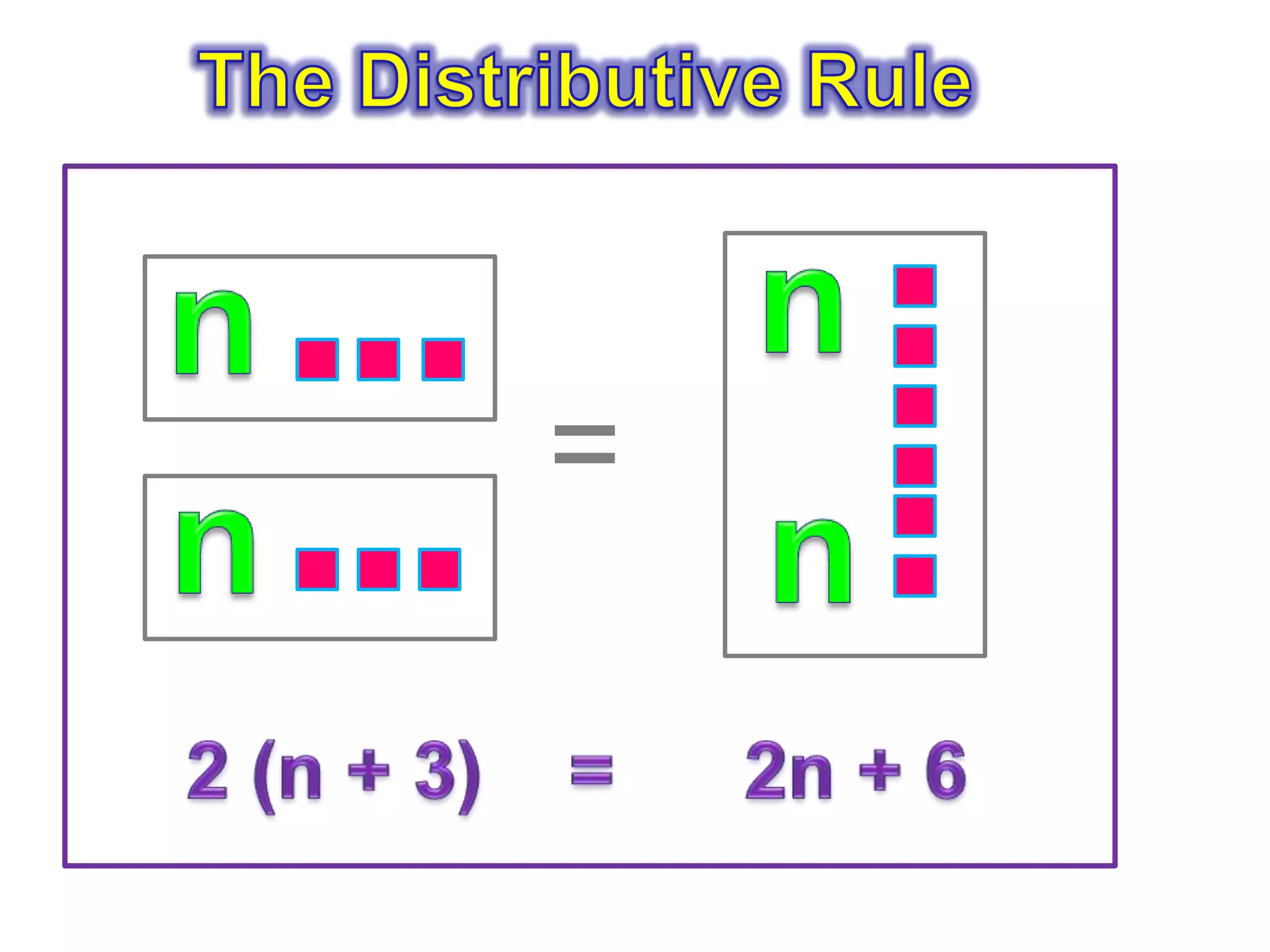
The document discusses three methods for solving the numeric expression 2(4+3): 1) Using the order of operations (BODMAS/PEMDAS) to evaluate the expression inside the parentheses first before multiplying. 2) Changing multiplication to addition by thinking of it as having "lots of" something. 3) Using the distributive property, where the number outside the parentheses is distributed across each term inside the parentheses.

1. =

2. For the numeric expression below, there
are three ways we can get to the answer:
2 (4 + 3) = 14
1) Using “BODMAS” or “Pemdas”
2) Changing multiply to adding “lots of”
3) Using the “Distributive Rule”

3. Use “BODMAS” / “Pemdas” Order
When we apply “BODMAS” or “Pemdas”
to the expression below, we need to do
“Brackets” (or “Parenthesis”), before we
do the “Multiplying”.
2 (4 + 3) = 2 x (4+3)
= 2 x (7)
=2x7
= 14

4. Change Multiply to Addition
Multiplying means having something several
times. (Eg. 2 x 5 means we have 2 lots of 5).
2 (4 + 3) = 2 x (4 + 3)
= 2 lots of (4 + 3)
4+3
+ 4+3
= 8 + 6 = 14

5. Use Distributive Rule
What is the answer to 2(4 + 3) ?
2 (4 + 3) = 2x4 + 2x3 = 14
The “2” outside the brackets is
multiplied onto everything that
is inside the brackets.

6. To help remember the Distributive Rule, think of
the number outside the brackets as a big Crab,
whose claw reaches into the bracket and grabs
both numbers and multiplies them.
Image Source: http://www.ceramicmosaicart.com

7. 2(n + 3) = 2xn + 2x3 = 2n + 6
We cannot do Algebra expressions
with BODMAS, because n+3 does
not simplify to a whole number.
So we have to use Distributive Rule.

8. 2(n + 3) = 2n + 6
We “expand” 2(n+3) to become
2n + 6 so that we can solve for “n”
in an equation like : 2n + 6 = 10
We can also do a graph of 2n + 6

9. In a car, the “Distributor”
puts electric charge onto
several different spark
plugs. The charge is
progressively distributed
across all of the car’s
spark plugs.
In Algebra we can
distribute one item to
multiply onto several
Image source: www.familycar.com
other different items.

10. Simplify: 2 ( y – 3 )
2 (y - 3) = 2xy - 2x3 = 2y - 6
The “2” outside the brackets multiplies
onto all letters and numbers that are
inside the brackets. We keep the
subtract sign all the way through.

11. Simplify: 2 ( 4e – y + 3 )
2 (4e - y + 3) = 2x4e – 2xy + 2x3
= 8e - 2y + 6
The “2” outside the brackets is multiplied
onto everything that is inside the brackets.

12. Simplify: -6 ( h – 3 )
-6 (h - 3) = -6xh - -6x3
-
= 6h + 18
or 18 – 6h
For the integer subtraction of minus
negative 18, we have changed to + 18.

13. Simplify: -9k2 ( k - 2 )
- 2
9k (k - 2) = -9k2xk - -9k2x2
= -9k3 - -18k2
= -9k3 + 18k2
Note that the above answer is usually rewritten as
18k2 – 9k3 so that we do not lead with a – sign.

14. Simplify: 2 ( a + 3 )
2 (a + 3) = 2a + 6
On average, nine times out of ten, the answer to
a Distributive Expansion will contain two terms.
If your answer does not have two terms, check
your work carefully. However, when some like
terms cancel such as 3b – 3b, then it is possible
to sometimes have a single term answer.

15. Simplify: 5c ( k – 4 ) + 3ck
5c (k - 4) + 3ck = 5cxk - 5cx4 + 3ck
= 5ck – 20c + 3ck Identify terms having
identical letters, and
then Combine these
“Like Terms” into a
= 5ck + 3ck - 20c simplified final answer.
= 8ck – 20c

16. Simplify: 2a(5b – 3) + 2(3a + 4ab)
2a(5b - 3) + 2(3a + 4ab)
= 2ax5b – 2ax3 + 2x3a + 2x4ab
= 10ab – 6a + 6a + 8ab
= 10ab – 6a + 6a + 8ab
= 18ab + 0 = 18ab

17. Simplify: 3b4(3b2 – 1) + 2b3(4b – b3)
3b4(3b2 – 1) + 2b3(4b – b3)
= 3b4x3b2 – 3b4x1 + 2b3x4b1 – 2b3xb3
= 9b6 – 3b4 + 8b4 – 2b6
= 9b6
– 3b 4
+ 8b 4
– 2b 6
= 7b6 + 5b4

18. http://passyworldofmathematics.com
Visit our site for Free Mathematics PowerPoints