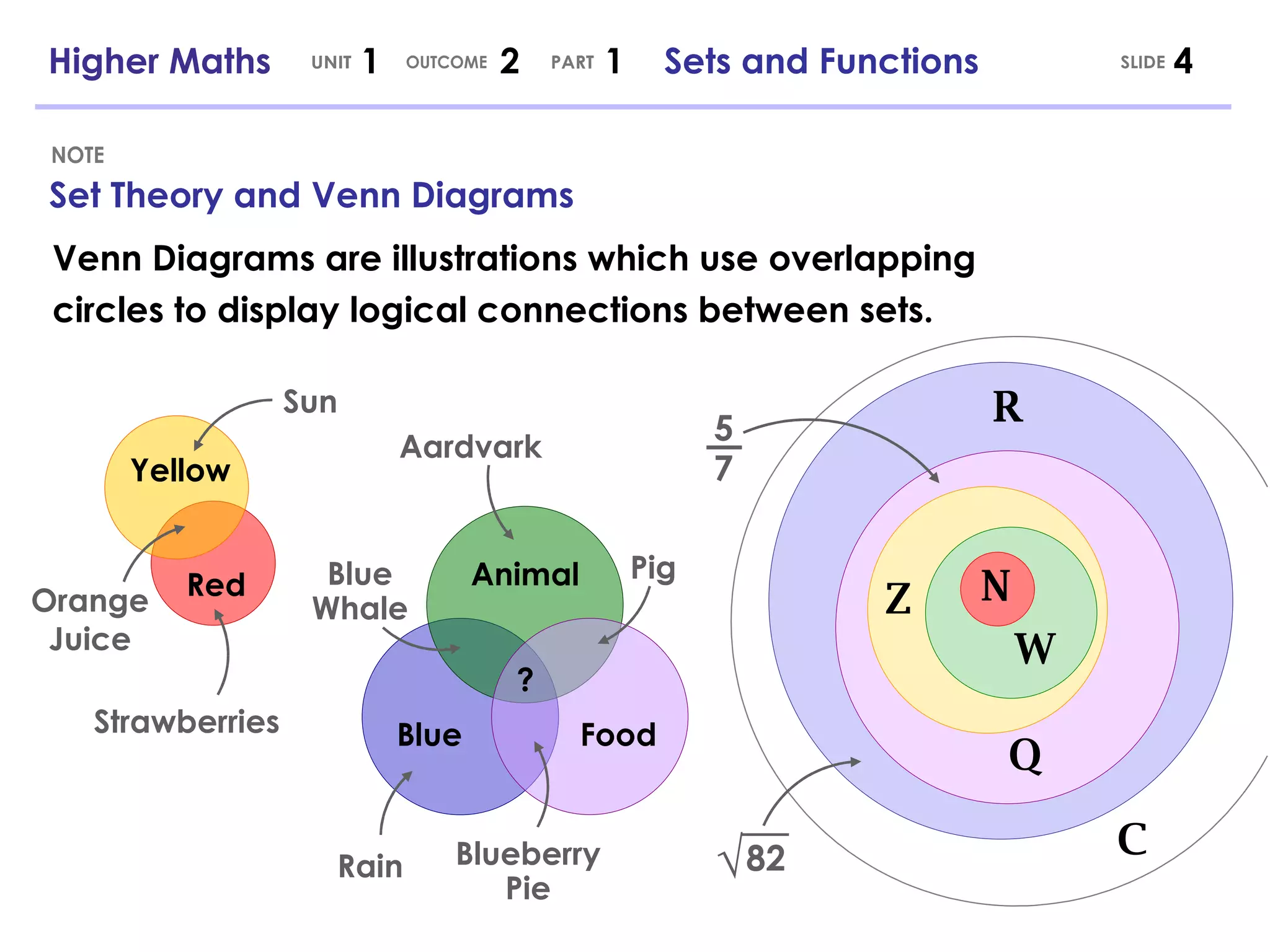
The document discusses key concepts in set theory and functions, including: - Sets can contain numbers, elements, and be represented using curly brackets. - Venn diagrams use overlapping circles to show logical connections between sets. - A function has a domain (input) and range (output), where each input is mapped to a unique output. - Composite functions combine other functions by substituting one into another. 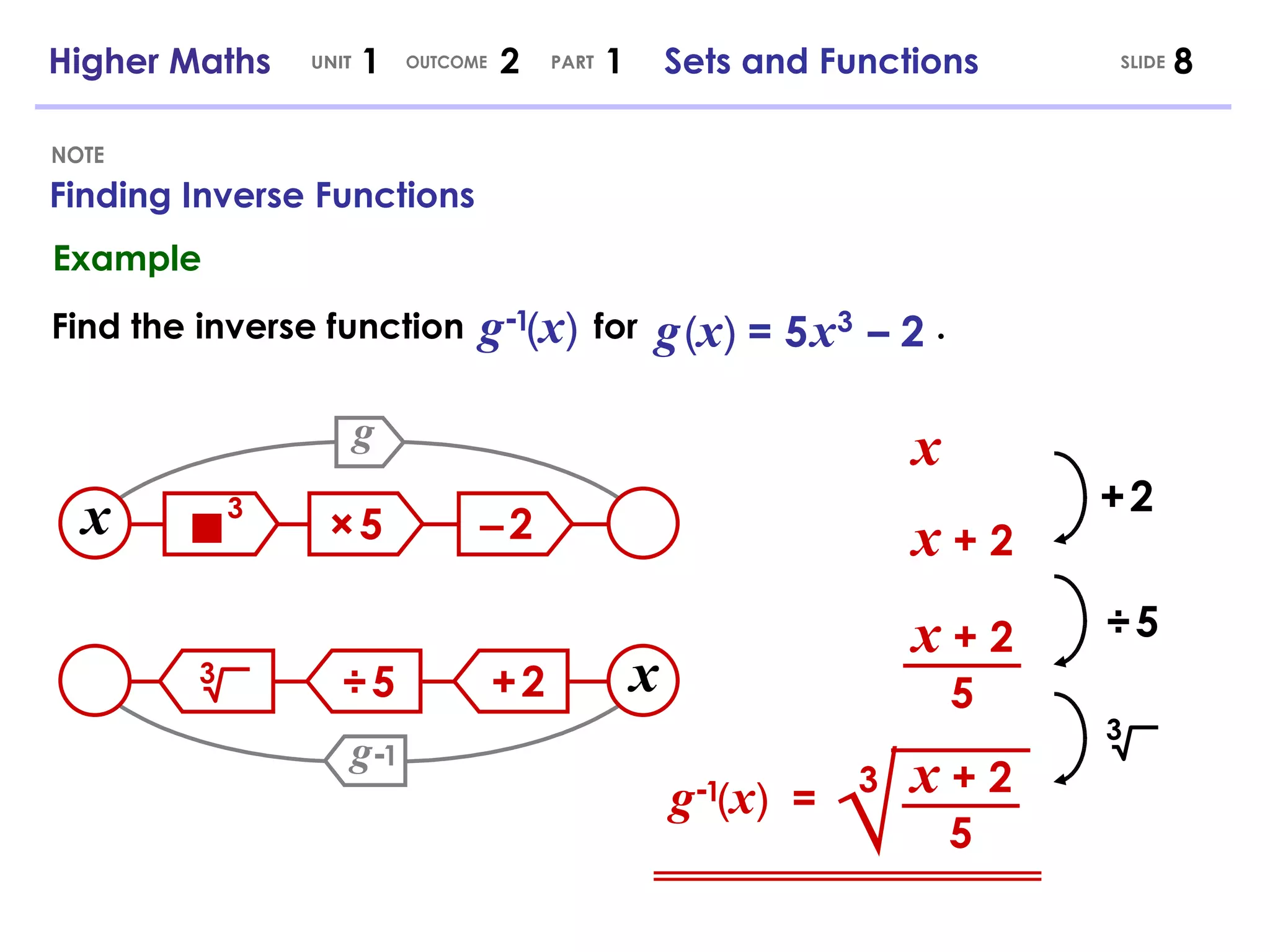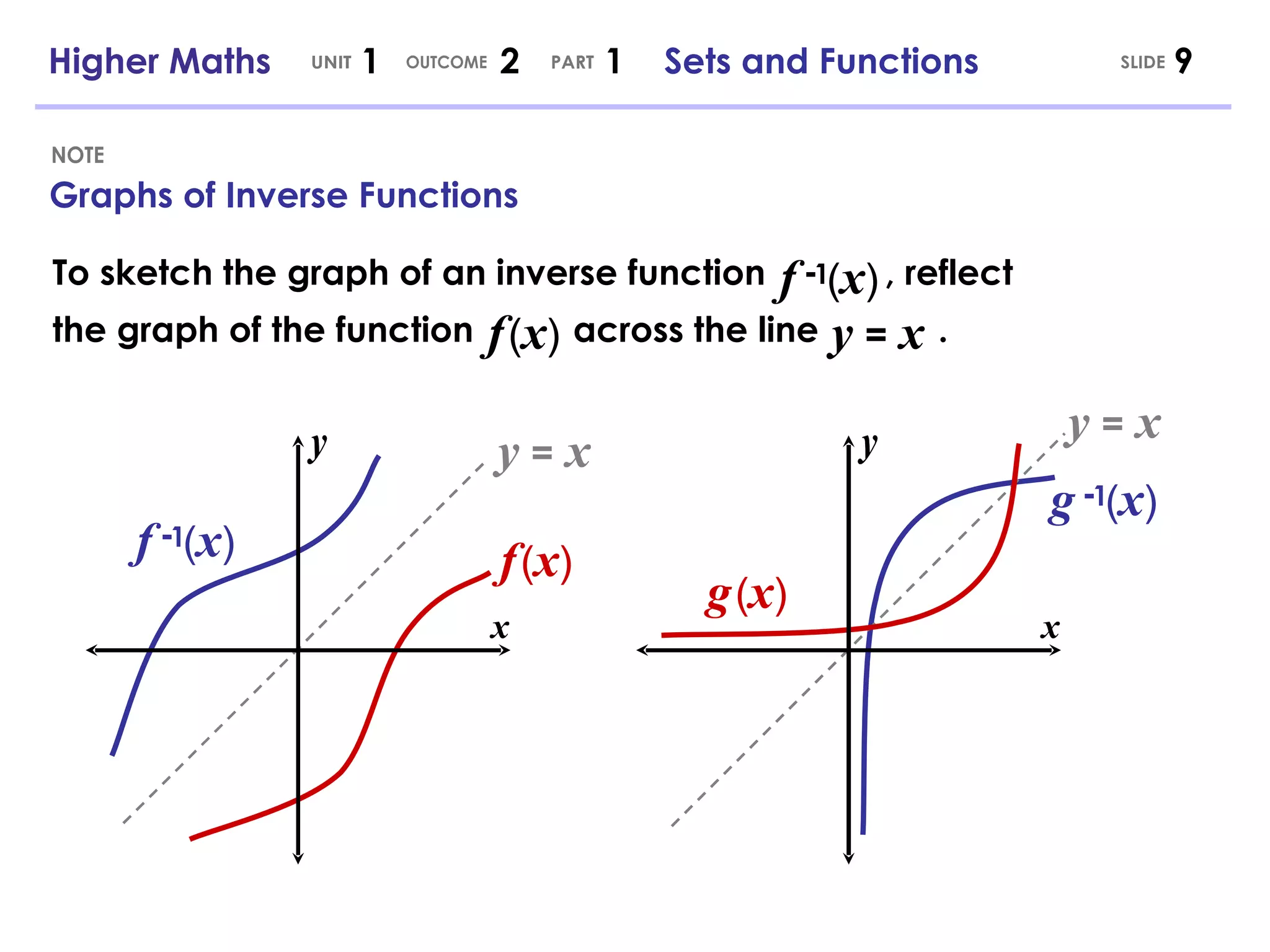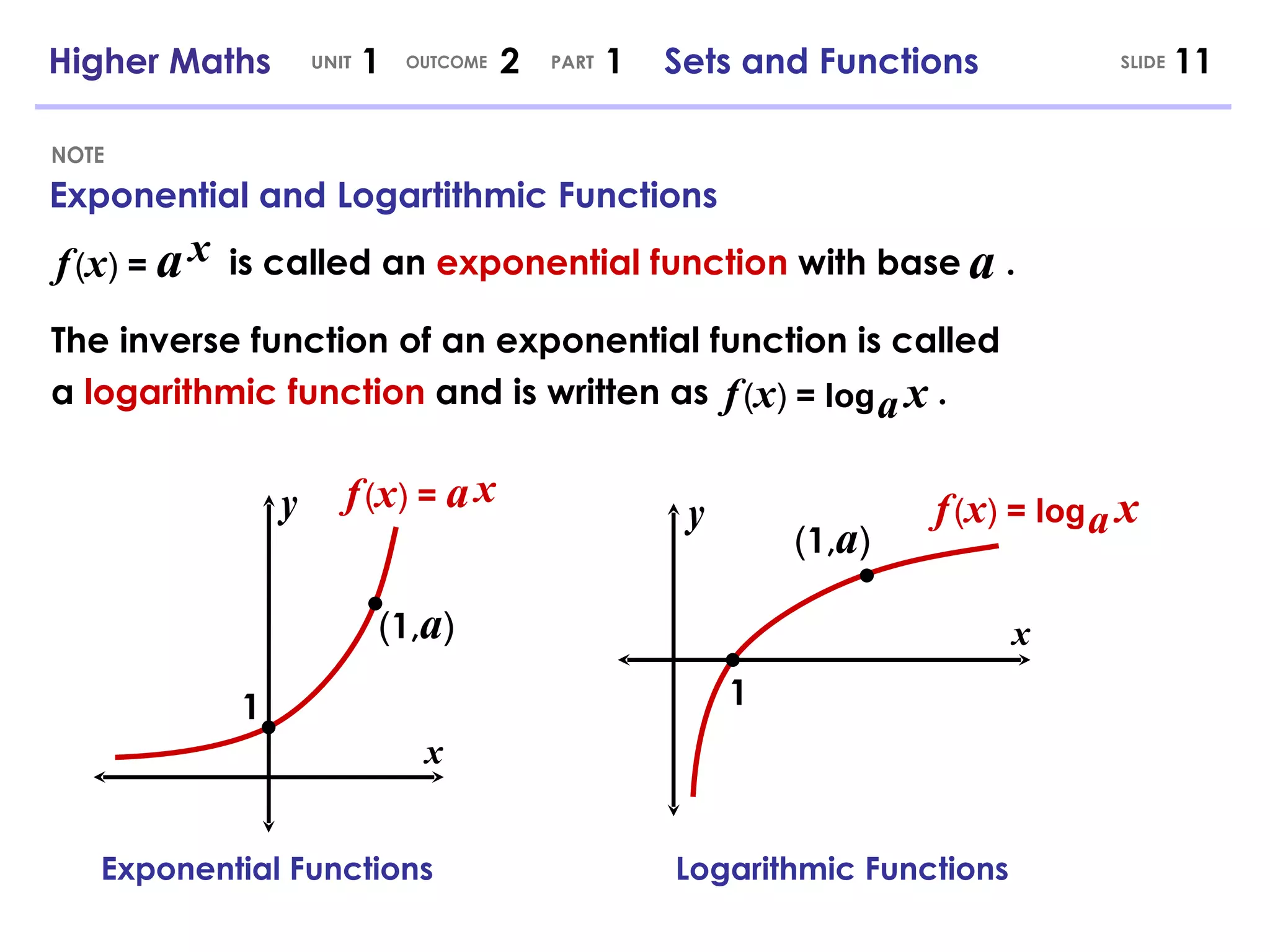- Inverse functions reverse the input and output of a function if it exists. 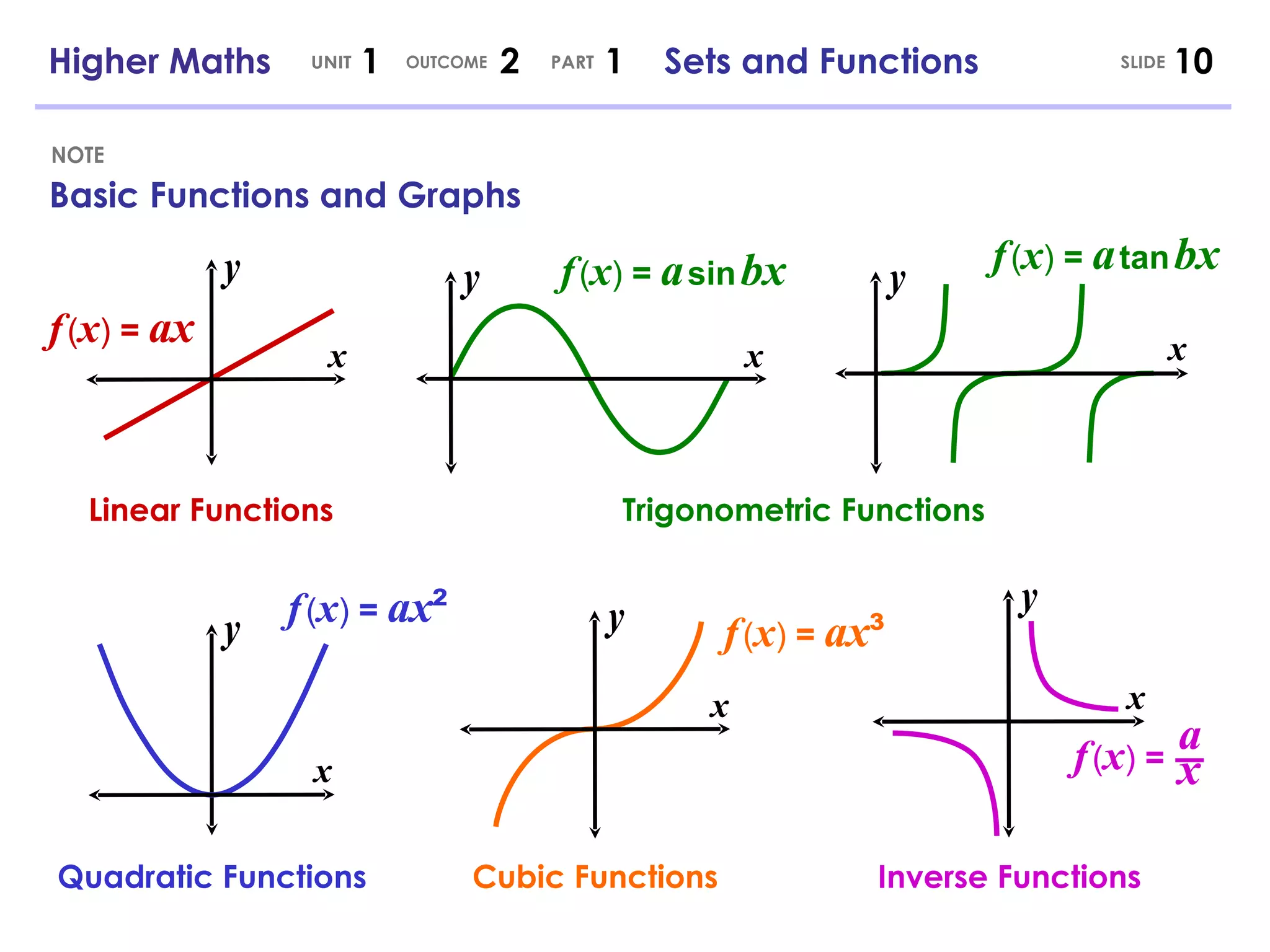- Common functions that can be graphed include linear, quadratic, trigonometric, cubic, exponential and logarithmic functions.

1. Higher Maths 1 2 Functions UNIT OUTCOME SLIDE

2. The symbol means ‘is an element of’. Introduction to Set Theory NOTE In Mathematics, the word set refers to a group of numbers or other types of elements. Sets are written as follows: Examples { 1, 2, 3, 4, 5, 6 } { -0.7, -0.2, 0.1 } { red, green, blue } 4 { 1, 2, 3, 4, 5 } Î Ï Î 7 { 1, 2, 3 } { 6, 7, 8 } { 6, 7, 8, 9 } Î Ï If A = { 0, 2, 4, 6, 8, … 20 } and B = { 1, 2, 3, 4, 5 } then B A Sets can also be named using letters: P = { 2, 3, 5, 7, 11, 13, 17, 19, 23, … } Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART

3. N W Z { 1, 2, 3, 4, 5, ... } { 0, 1, 2, 3, 4, 5, ... } { ... -3, -2, -1, 0, 1, 2, 3, ... } The Basic Number Sets NOTE Q Rational numbers Includes all integers, plus any number which can be written as a fraction. R √ 7 π Includes all rational numbers, plus irrational numbers such as or . Real numbers C Complex numbers Includes all numbers, even imaginary ones which do not exist. Whole numbers Integers Natural numbers N Î W Z Î Q Î Î R Î C 2 3 Î Q Ï √ - 1 R Examples Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART

4. Set Theory and Venn Diagrams NOTE Venn Diagrams are illustrations which use overlapping circles to display logical connections between sets. Blue Animal Food Pig Blueberry Pie Blue Whale ? Rain Red Yellow Orange Juice Sun Strawberries Aardvark N W Z Q R C √ 82 5 7 Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART

5. Function Domain and Range NOTE Any function can be thought of as having an input and an output. The ‘input’ is sometimes also known as the domain of the function, with the output referred to as the range . f ( x ) domain range Each number in the domain has a unique output number in the range. The function has the domain { -2, -1, 0, 1, 2, 3 } Find the range. Imporant Example f ( x ) = x 2 + 3 x f ( - 2 ) = 4 – 6 = - 2 f ( - 1 ) = 1 – 3 = - 2 f ( 0 ) = 0 + 0 = 0 f ( 1 ) = 1 + 3 = 4 f ( 2 ) = 4 + 6 = 10 Range = { -2, 0, 4, 10 } Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART

6. Composite Functions NOTE It is possible to combine functions by substituting one function into another. f ( x ) g ( x ) g ( ) f ( x ) is a composite function and is read ‘ ’. g ( ) f ( x ) g of f of x Important ≠ In general Given the functions Example g ( x ) = x + 3 f ( x ) = 2 x and find and . = 2 ( ) x + 3 = 2 x + 6 = ( ) + 3 2 x = 2 x + 3 f ( g ( x )) g ( f ( x )) g ( f ( x )) f ( g ( x )) Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART g ( ) f ( x ) f ( ) g ( x )

7. = x Inverse of a Function NOTE If a function also works backwards for each output number, it is possible to write the inverse of the function. f ( x ) f ( x ) = x 2 f ( 4 ) = 16 f ( -4 ) = 16 Not all functions have an inverse, e.g. Every output in the range must have only one input in the domain. does not have an inverse function. f ( x ) = x 2 domain range Note that = x x and f ( ) f ( x ) Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART f ( 16 ) = ? - 1 f ( ) - 1 f ( x ) f ( x ) - 1 - 1

8. Find the inverse function for . Finding Inverse Functions NOTE g ( x ) = 5 x 3 – 2 Example g ( x ) 3 × 5 – 2 g x x + 2 √ 3 ÷ 5 + 2 g x x x + 2 5 x + 2 5 3 g ( x ) = + 2 ÷ 5 3 Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART - 1 - 1 - 1

9. Graphs of Inverse Functions NOTE To sketch the graph of an inverse function , reflect the graph of the function across the line . f ( x ) y = x x y y = x f ( x ) x y y = x g ( x ) - 1 g ( x ) Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART f ( x ) - 1 f ( x ) - 1

10. Basic Functions and Graphs NOTE x y y x y x x x x y y y f ( x ) = ax f ( x ) = a sin bx f ( x ) = a tan bx f ( x ) = ax ² f ( x ) = ax ³ Linear Functions Quadratic Functions Trigonometric Functions Cubic Functions Inverse Functions Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART f ( x ) = a x

11. Exponential and Logartithmic Functions NOTE 1 f ( x ) = a x 1 ( 1 , a ) x y ( 1 , a ) x y is called an exponential function with base . Exponential Functions f ( x ) = a x a The inverse function of an exponential function is called a logarithmic function and is written as . Logarithmic Functions Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART f ( x ) = log x a f ( x ) = log x a

12. Finding Equations of Exponential Functions NOTE Higher Maths 1 2 1 Sets and Functions UNIT OUTCOME SLIDE PART It is possible to find the equation of any exponential function by substituting values of and for any point on the line. y = a + b x 2 ( 3 , 9 ) x y Example The diagram shows the graph of y = a + b Find the values of a and b . Substitute (0,2): x 2 = a + b 0 = 1 + b b = 1 x y Substitute (3,9): 9 = a + 1 3 a = 2 a = 8 3 y = 2 + 1 x