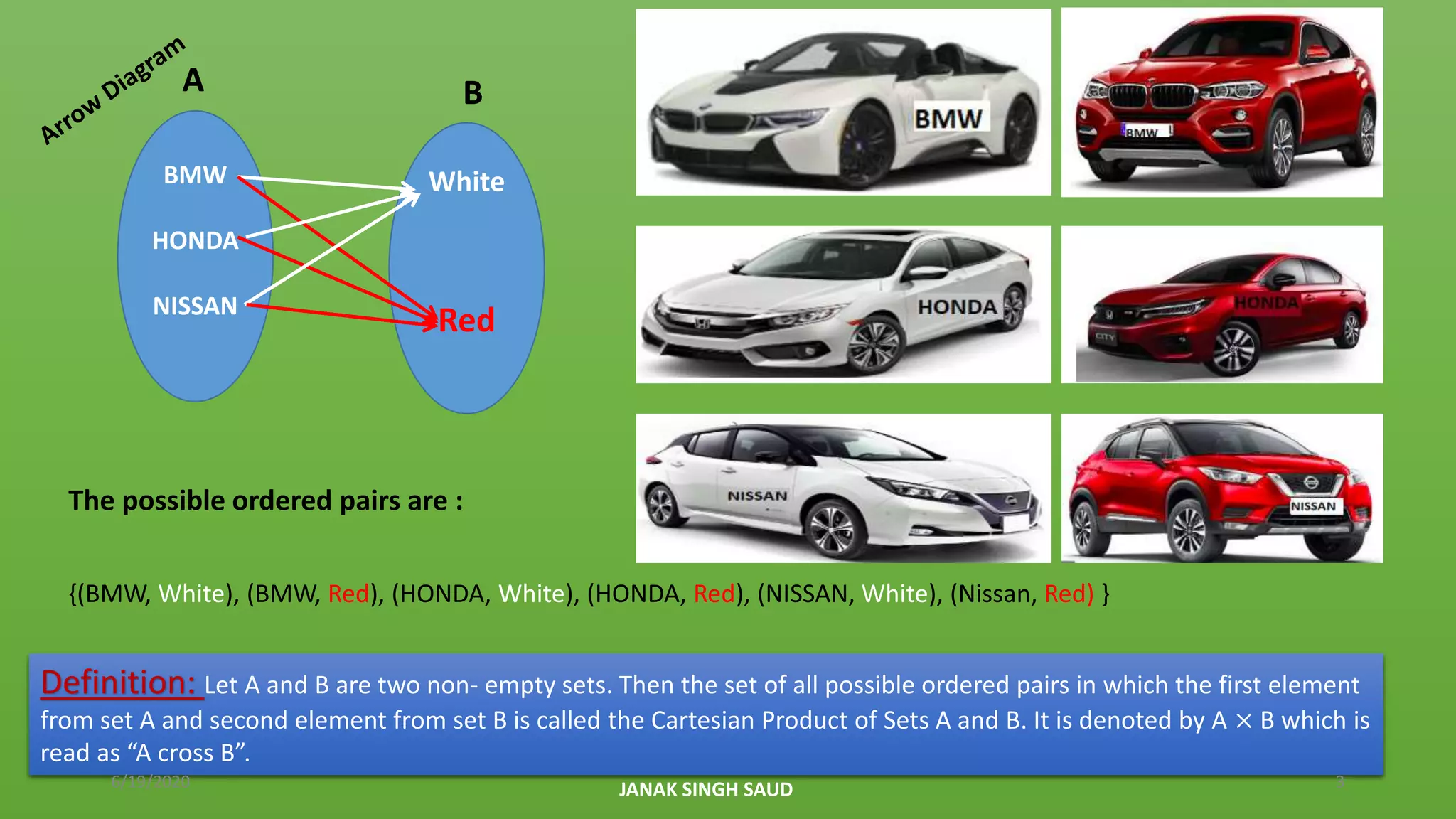
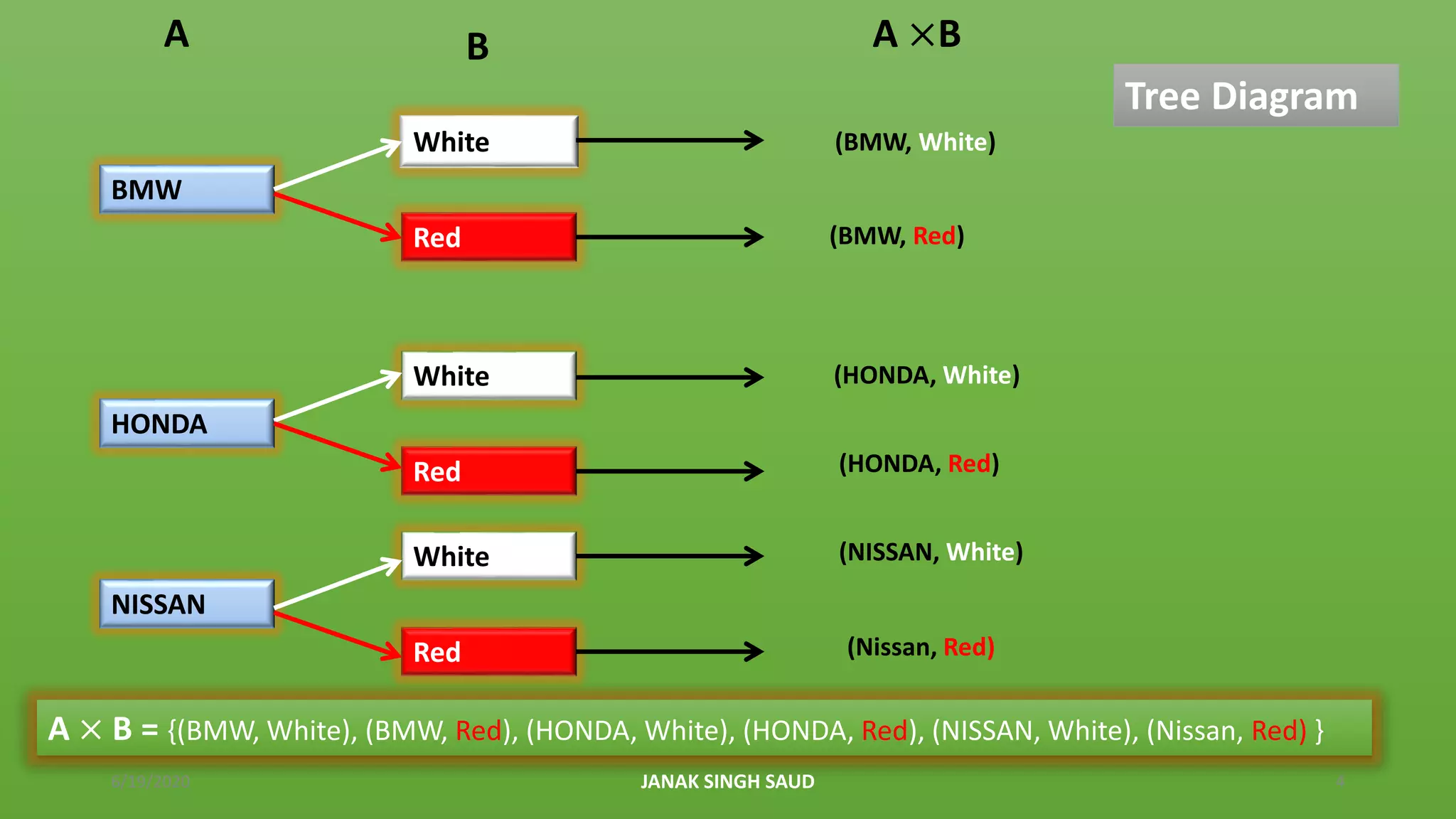
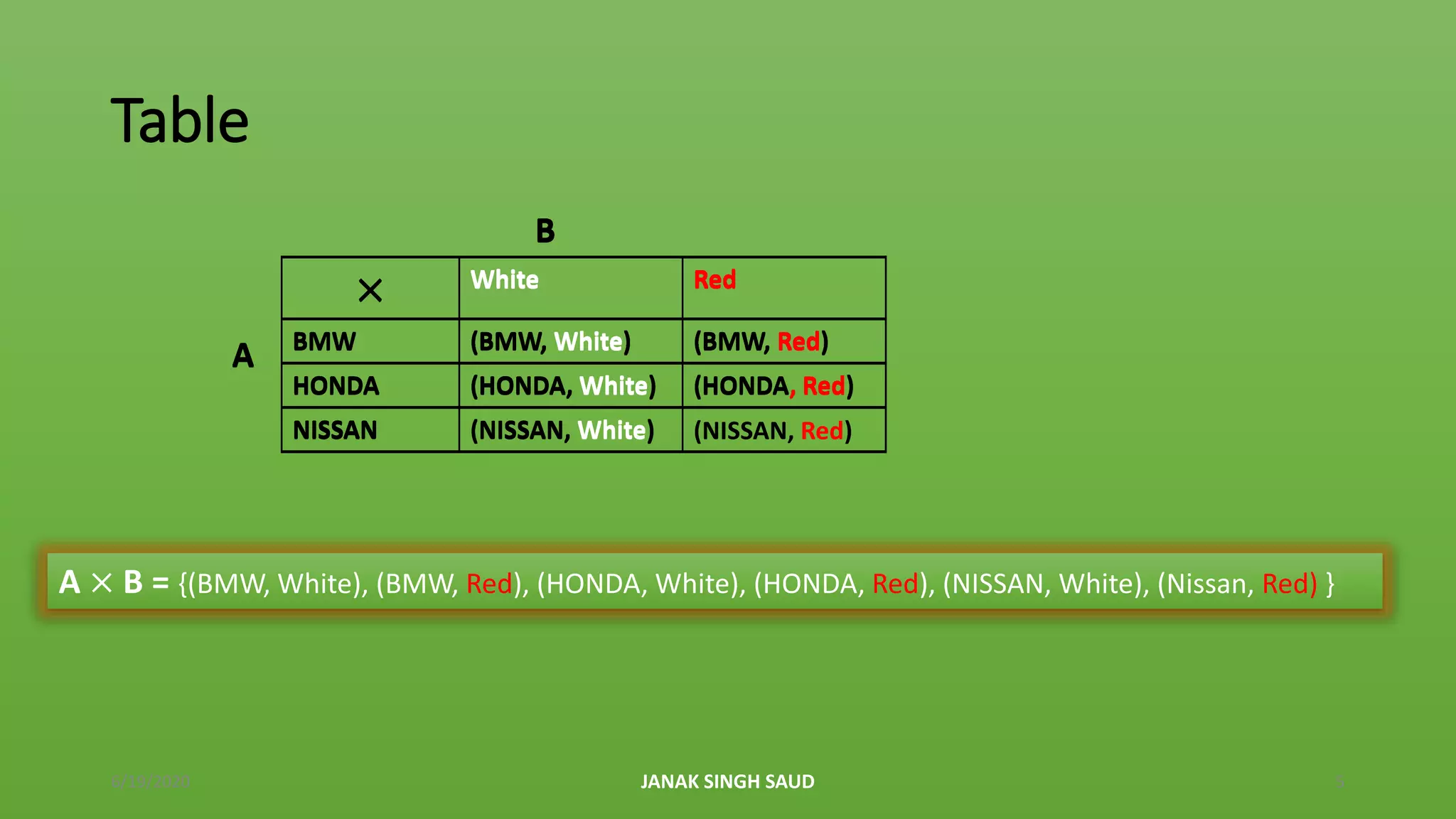
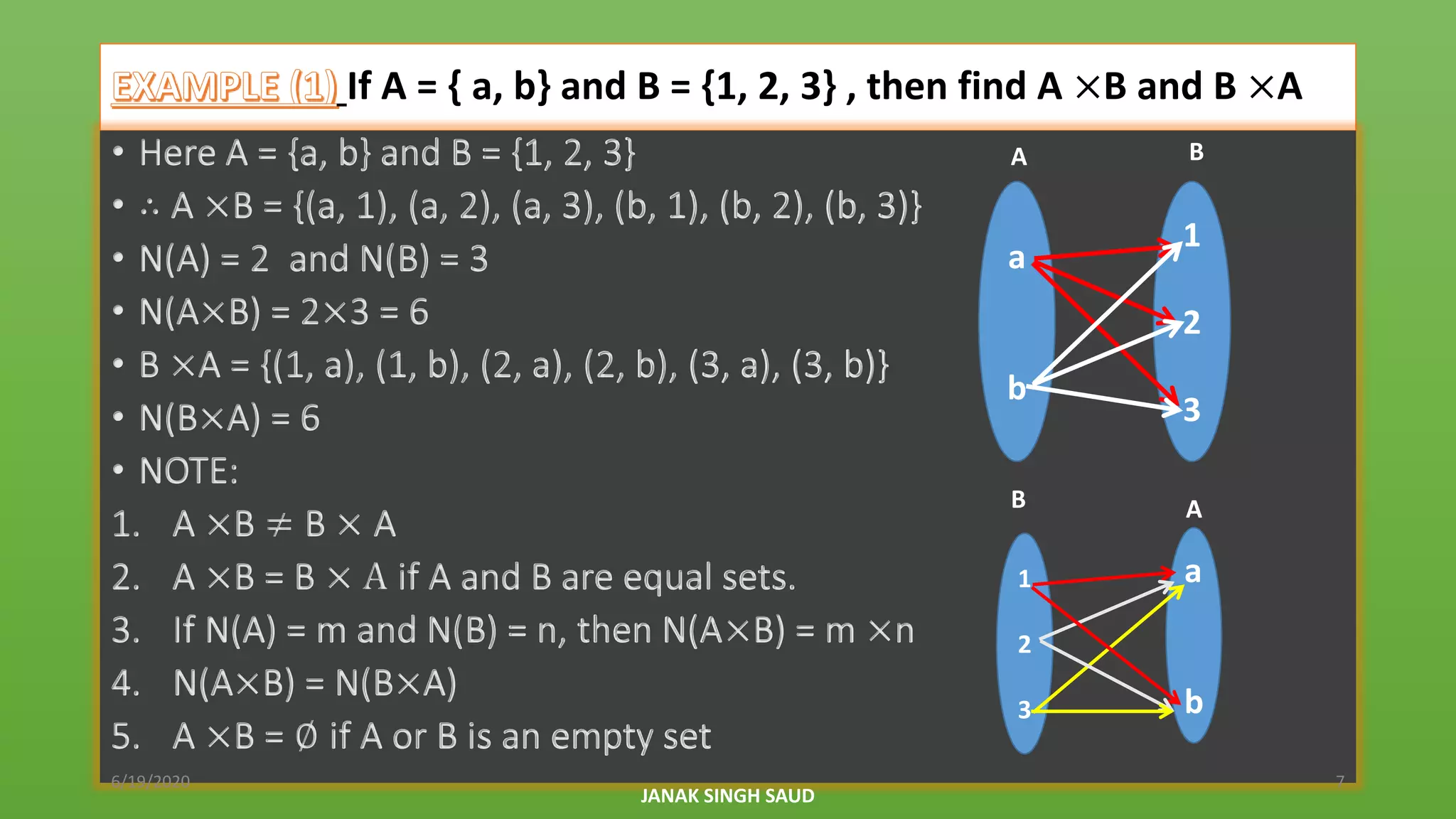
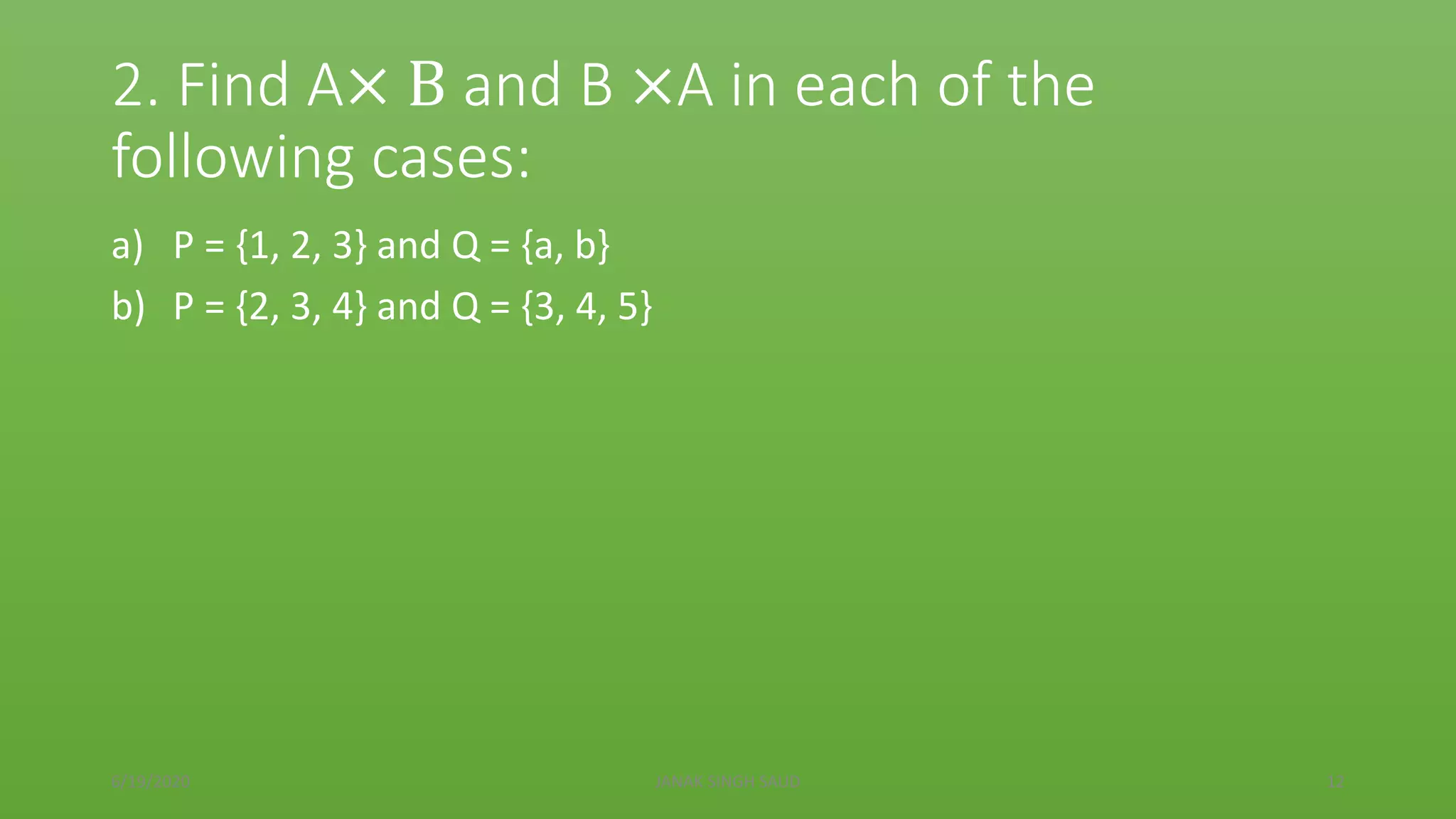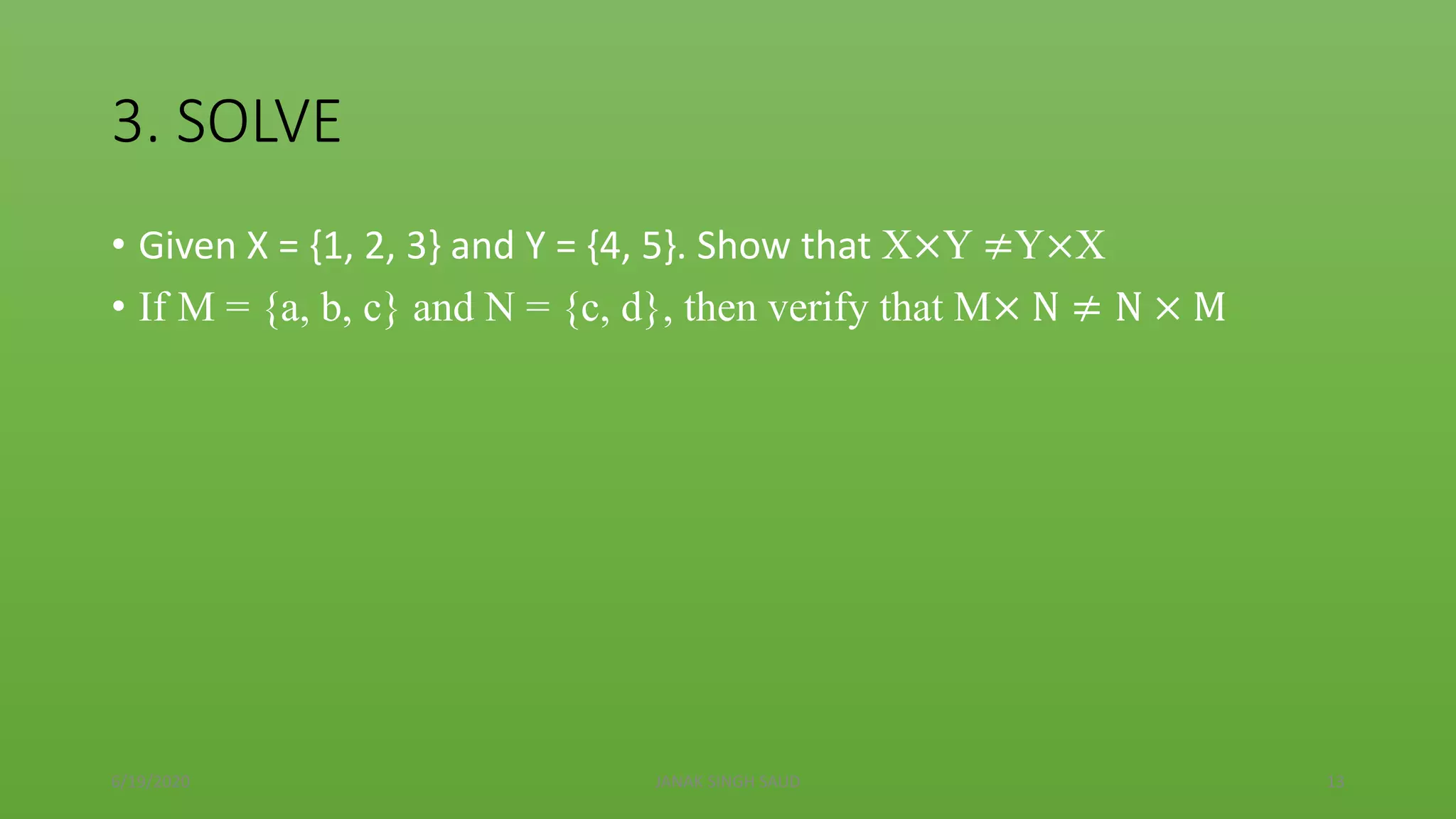The document explains the concept of Cartesian products of sets, using examples of car companies and color preferences to illustrate how to form ordered pairs from two non-empty sets. It includes definitions, properties of Cartesian products, and various examples to find Cartesian products of different sets, emphasizing that the order of sets matters. Additionally, it provides homework exercises for further practice on the topic.