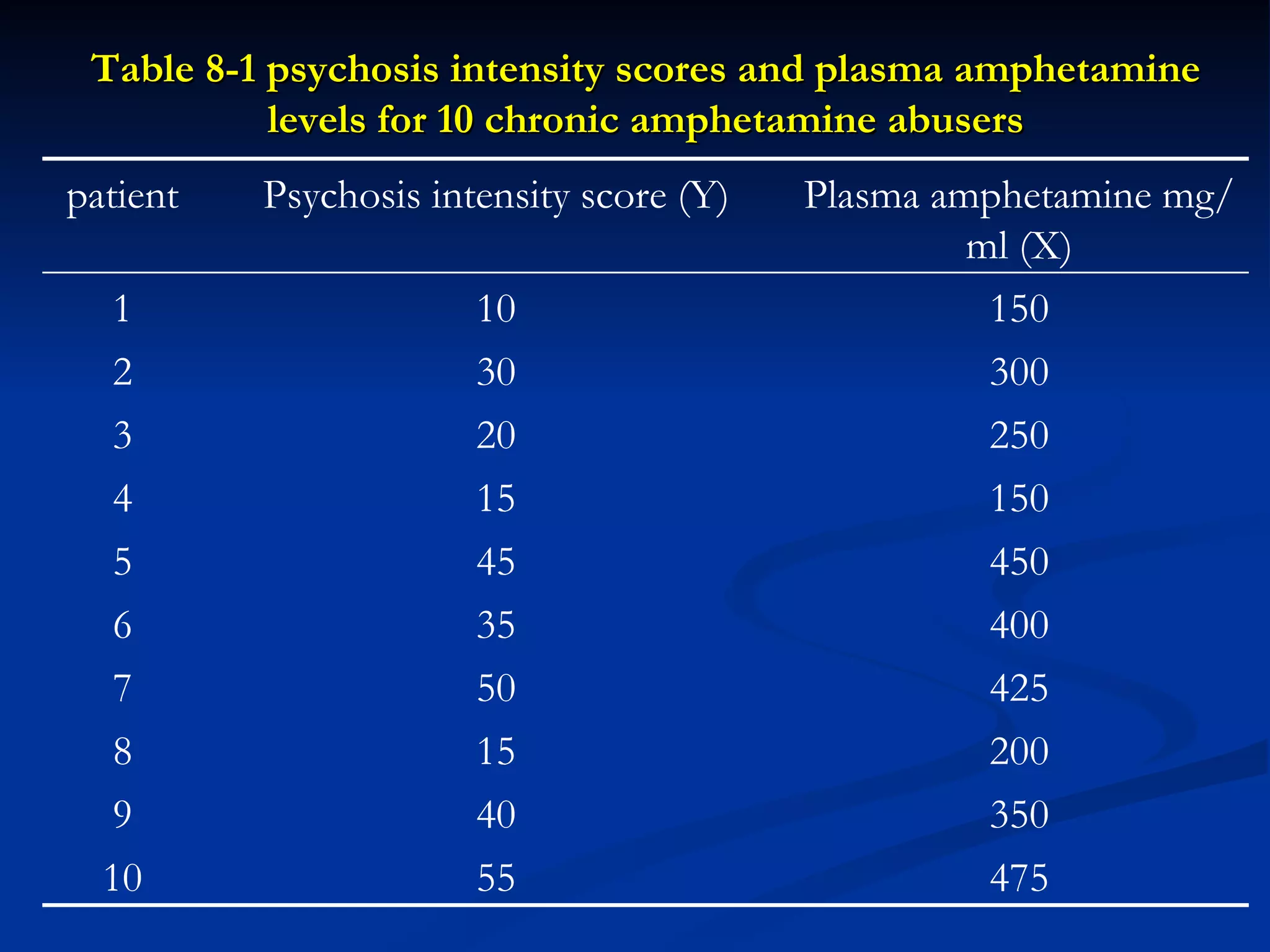
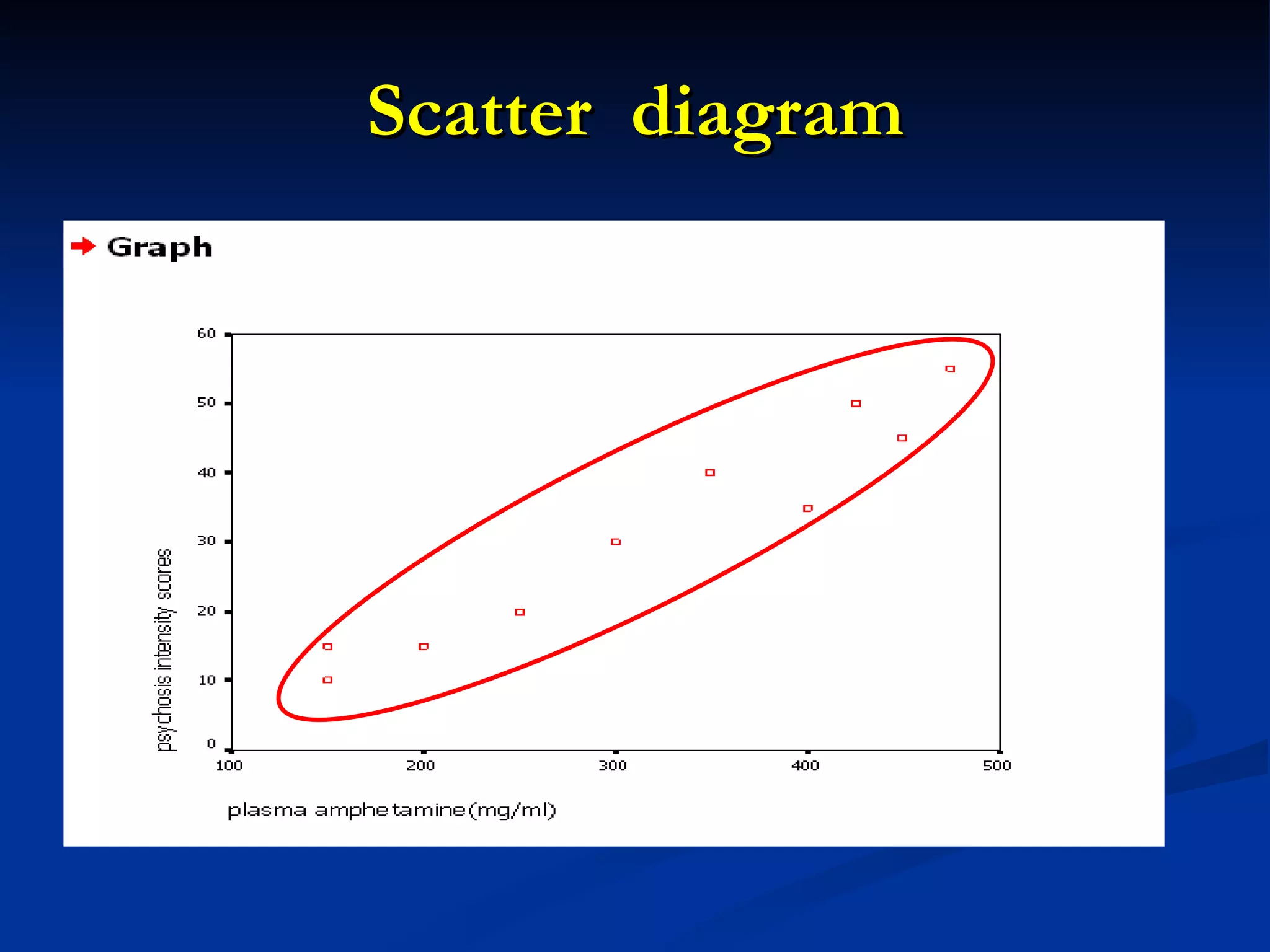
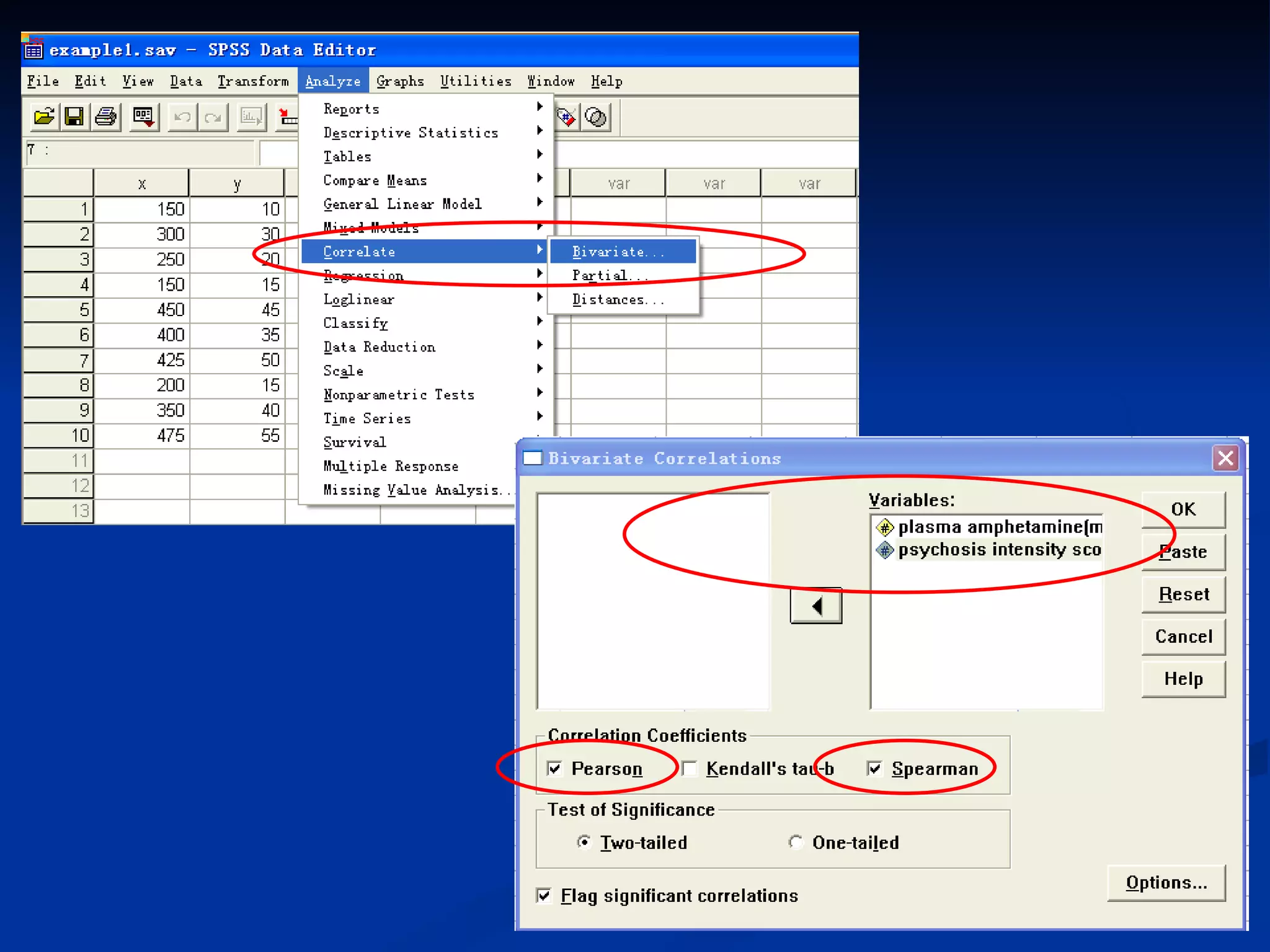
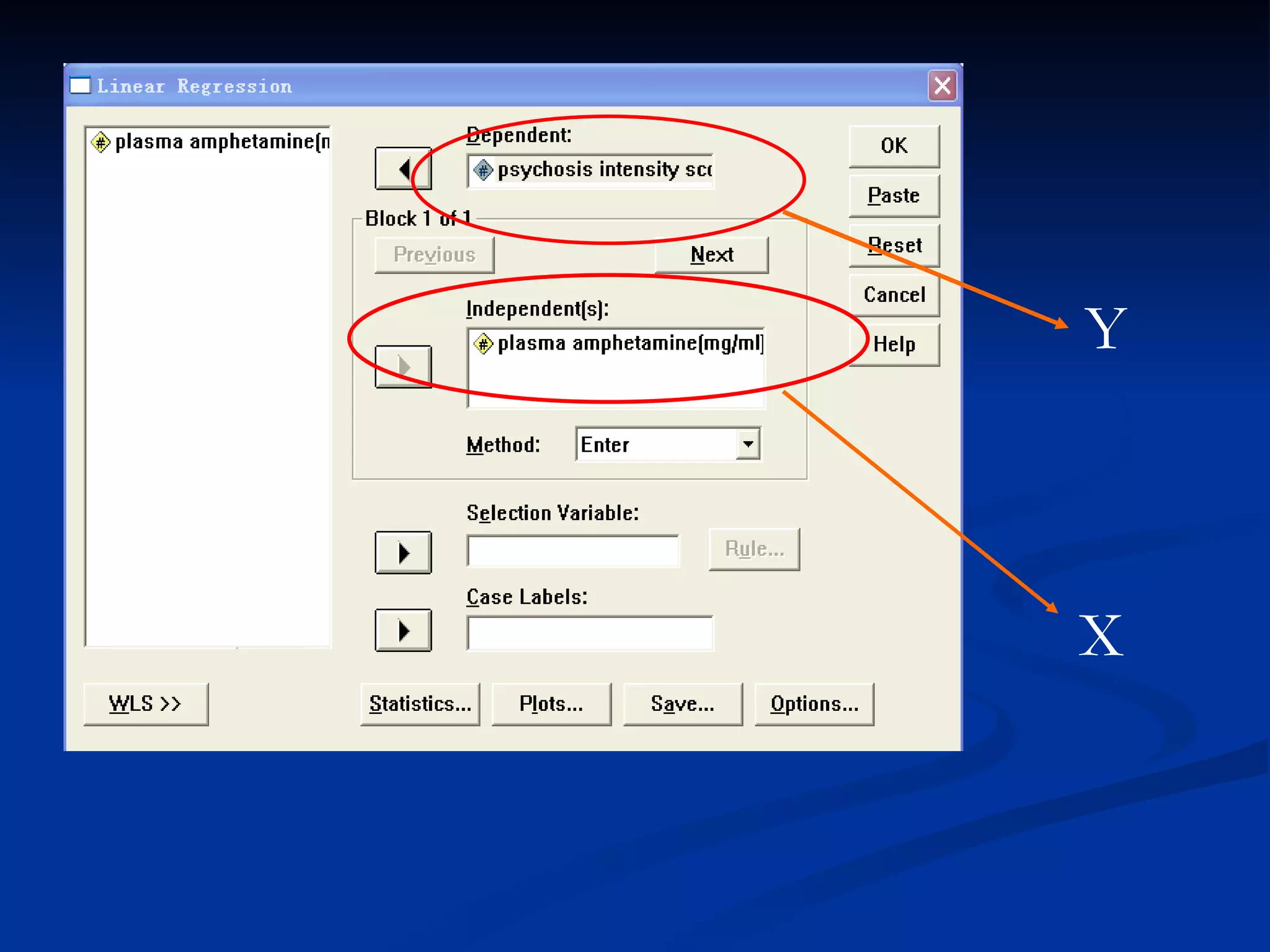
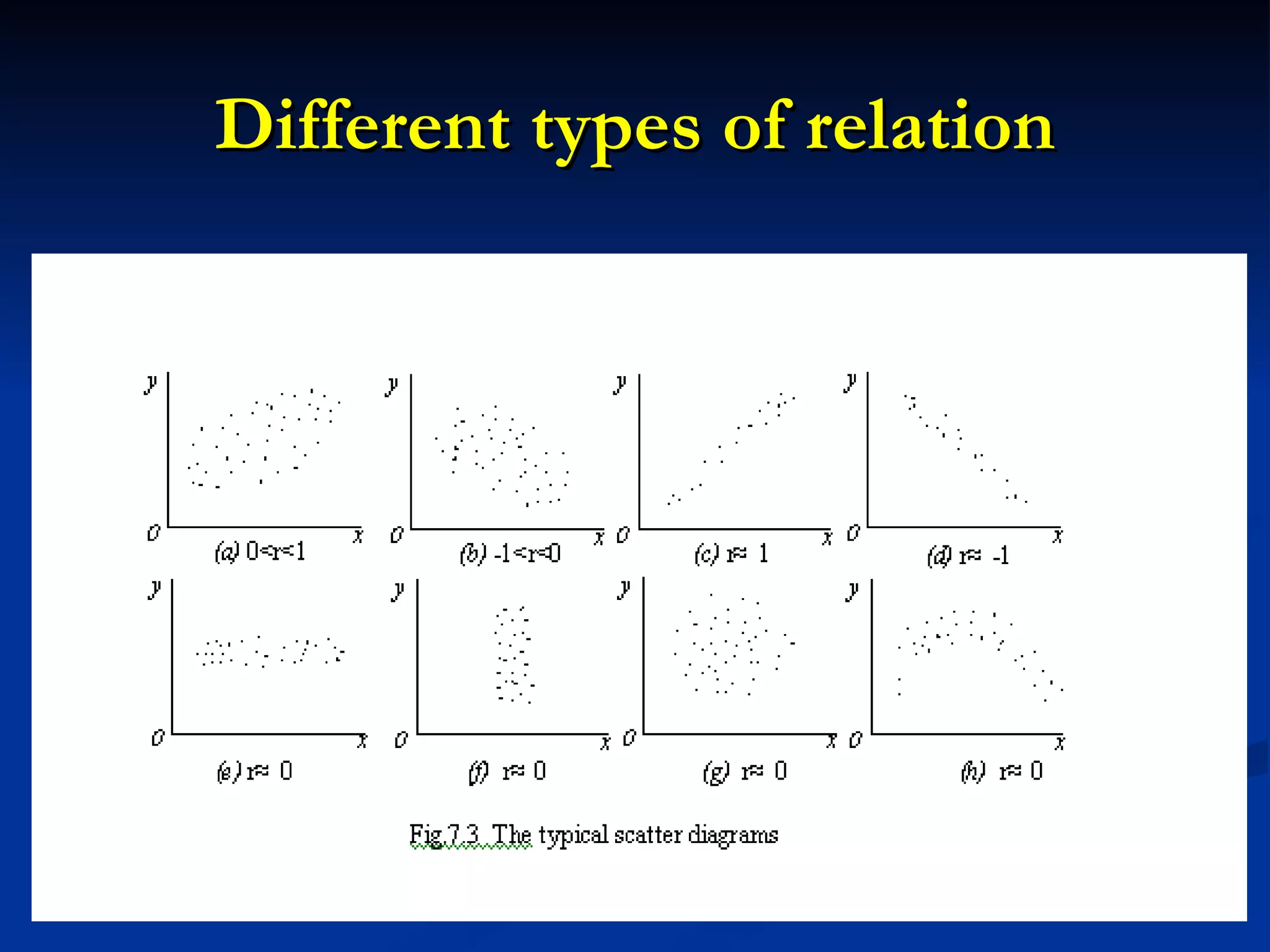
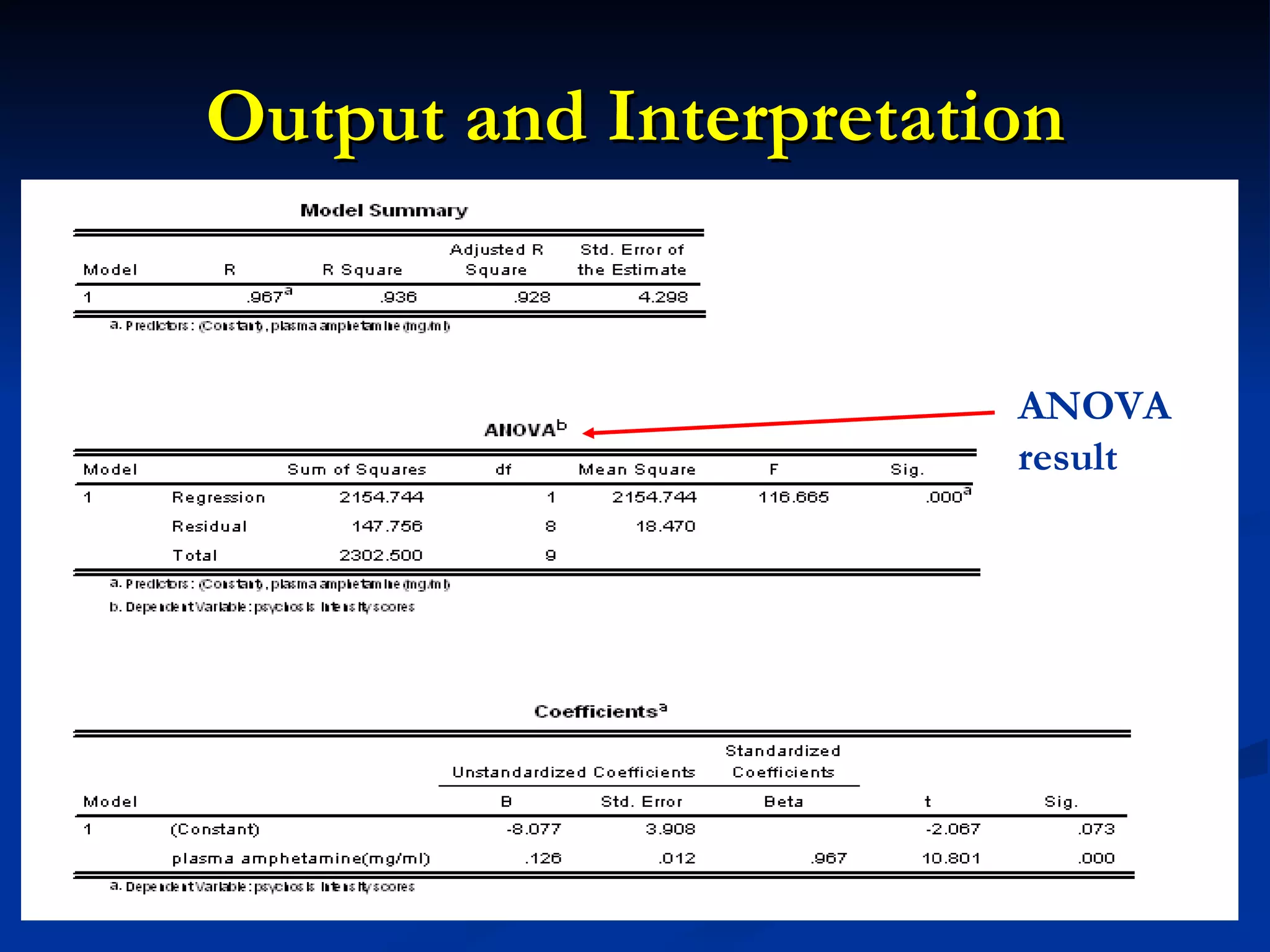
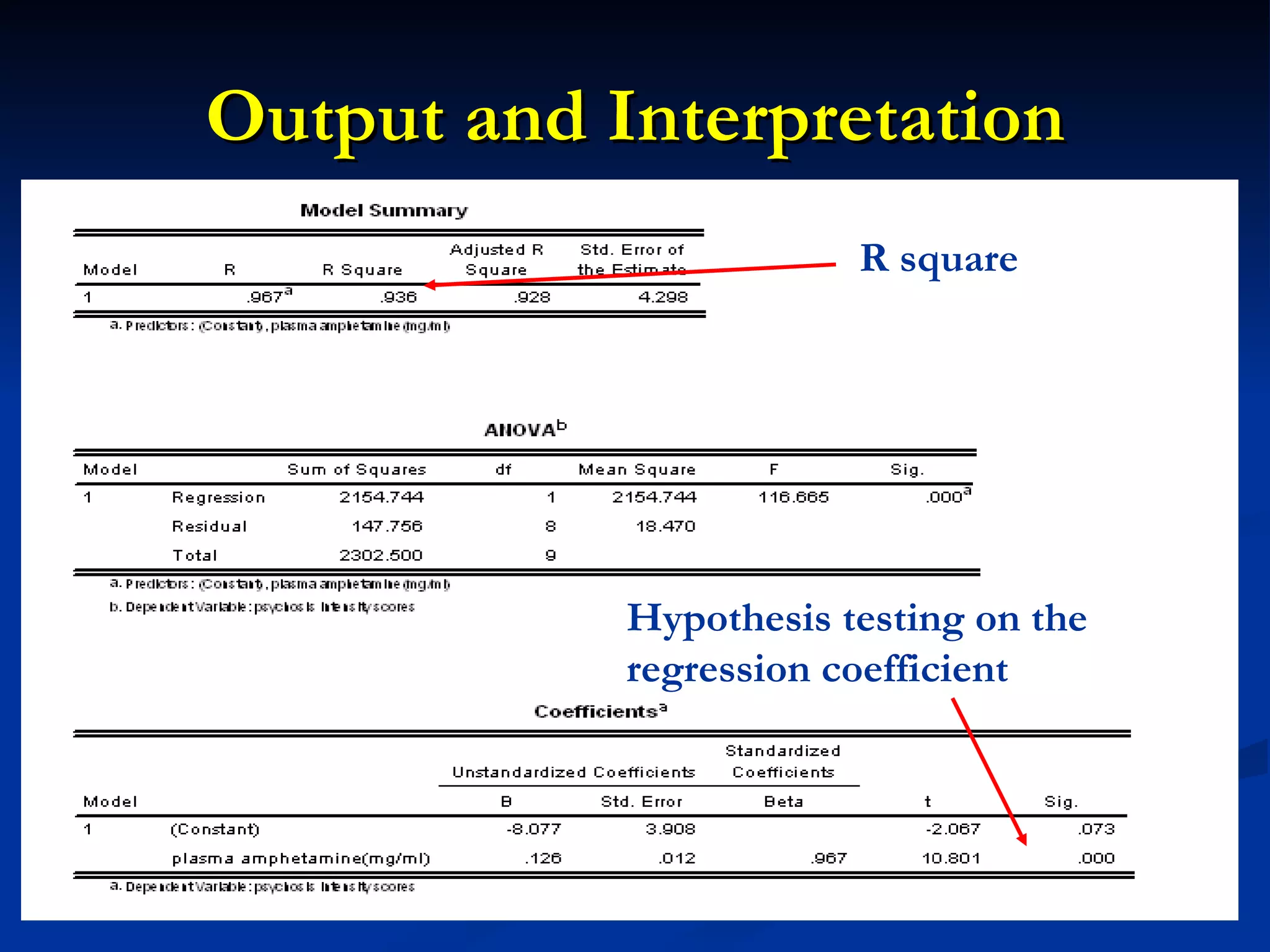
1. The document discusses linear correlation and regression between plasma amphetamine levels and amphetamine-induced psychosis scores using data from 10 patients. 2. A positive correlation was found between the two variables, and a linear regression equation was established to predict psychosis scores from amphetamine levels. 3. However, further statistical tests were needed to determine if the correlation and regression model could be generalized to the overall patient population.

1. Simple Linear Regression and Correlation Teaching Assistant: Zuo Xiaoyu Chapter 8

2. Outline Discussion part Steps of performing correlation and regression The Distinguish and connection Between Linear Correlation and Regression? Experiment part (incorporated in discussion part) Simple linear correlation Simple linear regression Exercise part

3. Discussion part

4. Case In a study of the relationship between plasma amphetamine levels and amphetamine-induced psychosis, 10 psychosis amphetamine abusers underwent psychiatric evaluation and were assigned a psychosis intensity score. At the same time, plasma amphetamine levels in these patients were determined. The results are shown in Table 8-1 Data file: discussion.sav

5. Table 8-1 psychosis intensity scores and plasma amphetamine levels for 10 chronic amphetamine abusers 475 55 10 350 40 9 200 15 8 425 50 7 400 35 6 450 45 5 150 15 4 250 20 3 300 30 2 150 10 1 Plasma amphetamine mg/ml (X) Psychosis intensity score (Y) patient

6. Question 1 Is there an intuitive relationship between plasma amphetamine levels and amphetamine-induced psychosis ? Scatter plot diagram Both variables are random

7. Procedure 8.1.2 Data File Variable Name: x; Variable Label: Psychosis intensity scores Variable Name: y; Variable Label: Plasma amphetamine (mg/ml) 8.1.3 Procedure (1) scatter diagram from the menus, choose: Analyze Graphs Scatter In scatter plot box, choose “simple”, click on button. In simple Scatter plot box, move y to the box of “Y Axis” and move x to the box of “X Axis”, click on button.

8. Procedure

9. Scatter diagram

10. Different types of relation

11. Question 2 How to quantify the relationship between plasma amphetamine levels and amphetamine-induced psychosis ? Correlation coefficient

12. Procedure (2) From the menus, choose: Analyze Correlate Bivariate, open “Bivariate Correlations” dialog box; move y and x to the “Variable” box; choose “Pearson” for Correlation Coefficients (default), or choose “spearman” if the variable are not normal distributed; click on button.

14. Output and Interpretation Pearson correlation Spearman correlation

15. Correlation Coefficient Pearson correlation coefficient Spearman’s rank correlation coefficient Both X and Y are random X and Y follow bivariate normal distribution

16. Spearman’s rank correlation coefficient It is useful to: ranked data As well as measurement data ---- not follow a normal distribution ; or not sure about the distribution; or not precisely measured or X or Y are ordinal variables

17. The direction of correlation? -- positive or negative The strength of correlation? high or not? -- Is the absolute value big enough? Complete correlation : +1 or -1, Understanding the r

18. Question 3 Can we draw a conclusion that plasma amphetamine levels are correlated with amphetamine-induced psychosis in population? What is the actual situation in population? Hypothesis testing on r Interval estimate of ρ

19. Hypothesis testing and interval estimation t test (Assume normal distribution) H 0 : ρ =0, H 1 : ρ ≠0 Interval estimation Inverse of hyperbolic tangent

20. Short summary Scatter plot diagram Compute correlation index (descriptive) Is the index statistically significant? -----hypothesis testing (inference) Interpretation of correlation coefficient (application)

21. Question 4 Could we predict the psychosis intensity score from the plasma amphetamine levels ? EX: Could we estimate and predict the psychosis intensity score when the plasma amphetamine levels is 440 and 460? Linear regression

22. Procedure From the menus, choose: Analyze Regression Linear, open “Linear Regression” dialog box; move y to “Dependent” box and move x to “Independent” box; click on button.

23. Y X

24. Output and Interpretation Intercept and slope

25. Question 5 Could this regression equation be established in the our studying population? Could we use this regression equation to predict the psychosis intensity score when the plasma amphetamine levels is 440 and 460, respectively? Hypothesis testing on the total equation--ANOVA

26. Output and Interpretation ANOVA result

27. Question 6 What is the proportion of the psychosis intensity score could we explain from the plasma amphetamine levels ? Could we view the plasma amphetamine levels as the influence factor of the amphetamine-induced psychosis ? R square Hypothesis testing on regression coefficient--- t -test

28. Output and Interpretation R square Hypothesis testing on the regression coefficient

29. Short summary Scatter plot diagram Compute the slope and intercept of sample (descriptive) Is the regression equation significant? -----ANOVA (inference) Is the regression coefficient significant? -----one sample t -test (inference) Interpretation and application of the regression model. (application)

30. Basic assumptions ---- LINE (1) L inear : There exists a linear tendency between the dependent variable and the independent variable (2) I ndependent : The individual observations are independent each other (3) N ormal : Given the value of, the corresponding follows a normal distribution (4) E qual variances : The variances of for different values of are all equal, denoted with .

31. Pre-requisite for linear regression (1) Linear : There exists a linear tendency between the dependent variable and the independent variable (2) Independent : The individual observations are independent each other (3) Normal : Given the value of, the corresponding follows a normal distribution (4) Equal variances : The variances of for different values of are all equal, denoted with .

32. Summary of discussion part

33. Two types of questions: Whether there is a linear relationship? -- Linear correlation How to predict one variable by another variable? -- Linear regression

34. Summary The Distinguish and connection Between Linear Correlation and Regression? Basic concepts Basic assumptions for data Correlation Coefficient and Regression Coefficient

35. Summary Assumptions: Correlation: Both X and Y are random Regression: (LINE) Y must be random X could be random or not random Correlation Coefficient (r)

36. Summary Linear Regression Equation, Regression Coefficient (b) Try to estimate  and  , getting

37. Summary Connection: When both X and Y are random 1) Same sign for Correlation Coefficient and Regression Coefficient 2) t tests are equivalent t r = t b 3) Determination Coefficient R=SS regression /SS total R=r 2

38. 3. For bivariate normal distributed variables, regression could be used to interpret correlation: The high determine coefficient indicates the X is closely correlated to Y. 2. The hypothesis testing for correlation coefficient and regression coefficient is equivalent. 1. The correlation coefficient has the same sign as regression coefficient. connection 1.investigate the quantitative dependency relationship between variables 2.prediction 3. variable selection investigate the quantitative association Application Independent variable be a normally distributed random variable. Bivariate normal distribution Pre-requisite Investigate the dependency relationship between the independent and dependent variables. Quantify the relationship between two or more variables. Implication Regression Correlation

39. Discussion——true or false? 1. Put any two variables together for correlation and regression ? ( × They must have some relation in subject matter) 2. Correlation and regression mean causality? ( × sometimes may be indirect relation or even no any real relation) 3. A big value of r means a big regression coefficient b ? ( × ) 4. To reject means that the correlation is strong? (× just only means )

40. Discussion——true or false? 5. A regression equation is statistically significant means that one can well predict Y by X ? ( × well predict or not depends on coefficient of determination) 6. The regression equation is allowed to be applied beyond the range of the data set ? ( × )

41. To explore the correlation between the heights of father and son, 20 graduate male students were randomly selected from a name list of graduates in a high school. The heights (cm) of fathers and sons were measured. (1) What is the relationship of the heights of father and son? (2) Can we predict the son’s height if a father with height 166 cm? Exercise

42. Heights (cm) of 20 pairs of father and son

43. About Homework Test for D ifference —— treated as paired design Test for A ssociation —— treated as independent design McNemar

44. Assignment P 129 N. 5

45. Thank you!!!