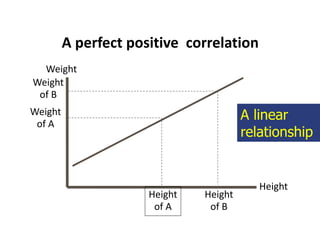
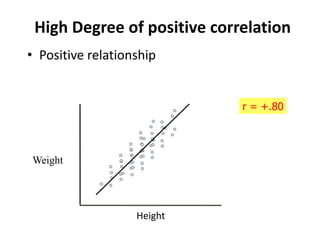
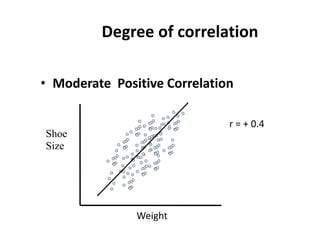
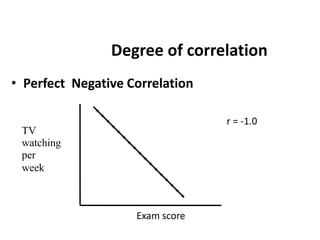
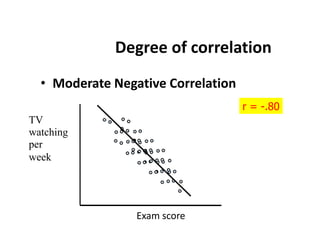
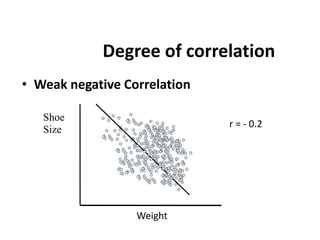
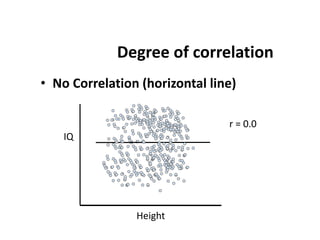
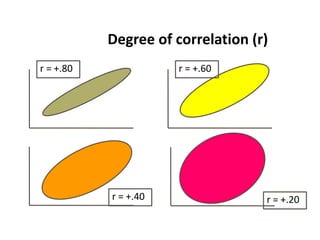
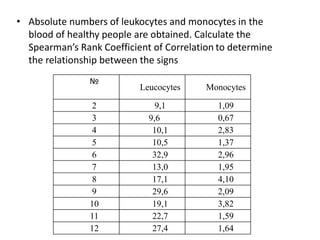
This document discusses correlation and regression analysis. It defines correlation as the degree of relationship between two variables and introduces the correlation coefficient r as a measure of correlation. It describes properties of r including that it ranges from -1 to 1, with positive values indicating an increasing relationship and negative values a decreasing relationship. Methods for studying correlation are presented, including scatter diagrams and Pearson's and Spearman's correlation coefficients. The relationship between correlation and regression is also discussed.

1. Correlation and Regression
Analysis
• Basic concepts and tasks of correlation analysis
• Pearson correlation coefficient and its properties
• Spearman's rank correlation coefficient
• The relationship of regression and correlation
• Coefficient of determination
• The statistical significance of correlation.
• Regression equations
• Estimation of the parameters of the regression
equation for the sample
• Testing the hypothesis of the significance of the
regression coefficient

2. CORRELATION

3. Correlation
• The degree of relationship between the variables
under consideration is measure through the
correlation analysis.
• The measure of correlation called the correlation
coefficient .
• The degree of relationship is expressed by coefficient
which range from correlation ( -1 ≤ r ≥ +1)
• The direction of change is indicated by a sign.
• The correlation analysis enable us to have an idea
about the degree & direction of the relationship
between the two variables under study.

4. More examples
• Positive relationships
• water consumption
and temperature.
• study time and
grades.
• Negative relationships:
• alcohol consumption
and driving ability.
• Price & quantity
demanded

5. Methods of Studying Correlation
• Scatter Diagram Method
• Graphic Method
• Karl Pearson’s Coefficient Spearman’s
Rank Coefficient of Correlation

6. Scatter Diagram Method
• Scatter Diagram is a graph of observed
plotted points where each points
represents the values of X & Y as a
coordinate. It portrays the relationship
between these two variables graphically.

7. A perfect positive correlation
Height
Weight
Height
of A
Weight
of A
Height
of B
Weight
of B
A linear
relationship

8. High Degree of positive correlation
• Positive relationship
Height
Weight
r = +.80

9. Degree of correlation
• Moderate Positive Correlation
Weight
Shoe
Size
r = + 0.4

10. Degree of correlation
• Perfect Negative Correlation
Exam score
TV
watching
per
week
r = -1.0

11. Degree of correlation
• Moderate Negative Correlation
Exam score
TV
watching
per
week
r = -.80

12. Degree of correlation
• Weak negative Correlation
Weight
Shoe
Size
r = - 0.2

13. Degree of correlation
• No Correlation (horizontal line)
Height
IQ
r = 0.0

14. Degree of correlation (r)
r = +.80 r = +.60
r = +.40 r = +.20

15. 2) Direction of the Relationship
• Positive relationship – Variables change in the
same direction.
• As X is increasing, Y is increasing
• As X is decreasing, Y is decreasing
– E.g., As height increases, so does weight.
• Negative relationship – Variables change in
opposite directions.
• As X is increasing, Y is decreasing
• As X is decreasing, Y is increasing
– E.g., As TV time increases, grades decrease
Indicated by sign; (+) or (-)

16. Karl Pearson's
Coefficient of Correlation
 

 







 n
i
n
i
i
i
n
i
i
i
X
x
X
x
X
x
X
x
r
1 1
2
2
2
2
1
1
1
2
2
1
1
)
(
)
(
)
(
)
(

17. Spearman’s Rank Coefficient of
Correlation
• When statistical series in which the variables
under study are not capable of quantitative
measurement but can be arranged in serial order,
in such situation pearson’s correlation coefficient
can not be used in such case Spearman Rank
correlation can be used.

18. Rank Correlation Coefficient (R)
Problems where actual rank are given.
1) Calculate the difference ‘D’ of two Ranks i.e.
(R1 – R2).
2) Square the difference & calculate the sum of
the difference i.e. ∑D2
3) Substitute the values obtained in the
formula.

19. • Absolute numbers of leukocytes and monocytes in the
blood of healthy people are obtained. Calculate the
Spearman’s Rank Coefficient of Correlation to determine
the relationship between the signs
№
Leucocytes Monocytes
2 9,1 1,09
3 9,6 0,67
4 10,1 2,83
5 10,5 1,37
6 32,9 2,96
7 13,0 1,95
8 17,1 4,10
9 29,6 2,09
10 19,1 3,82
11 22,7 1,59
12 27,4 1,64

20. The regression model is a statistical procedure that allows a
researcher to estimate the linear, or straight line,
relationship that relates two or more variables. This linear
relationship summarizes the amount of change in one
variable that is associated with change in another variable
or variables.
The model can also be tested for statistical significance, to
test whether the observed linear relationship could have
emerged by chance or not.
the two variable linear regression model is follow
Regression

21. • The straight line connecting any two variables
X and Y can be stated algebraically as
0
1 b
x
b
y 

x
b
y
n
x
b
y
b
n
i
n
i
i
i
1
1 1
1
0 



 
 





 2
1
)
(
)
)(
(
x
x
y
y
x
x
b
i
i
i