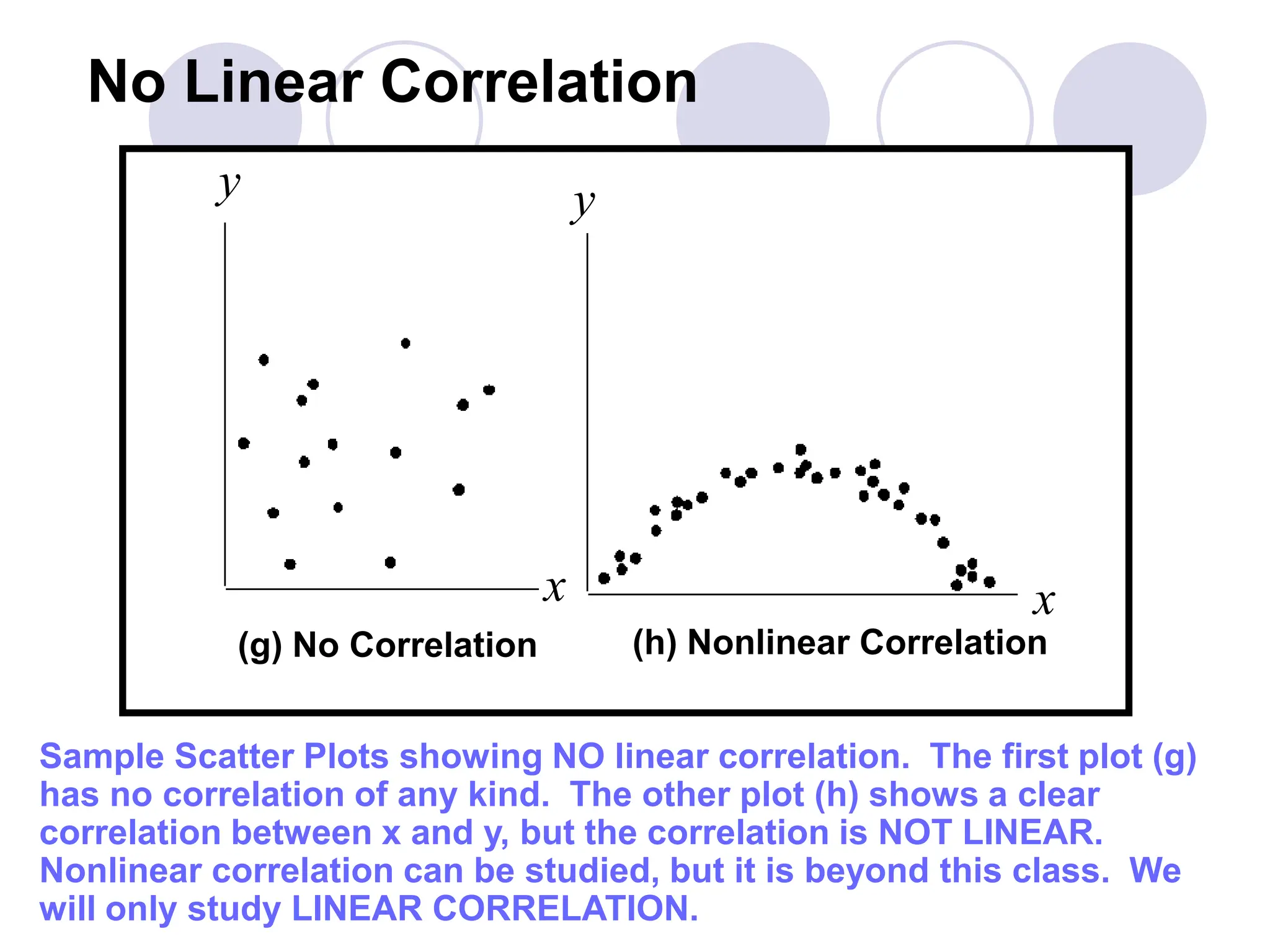
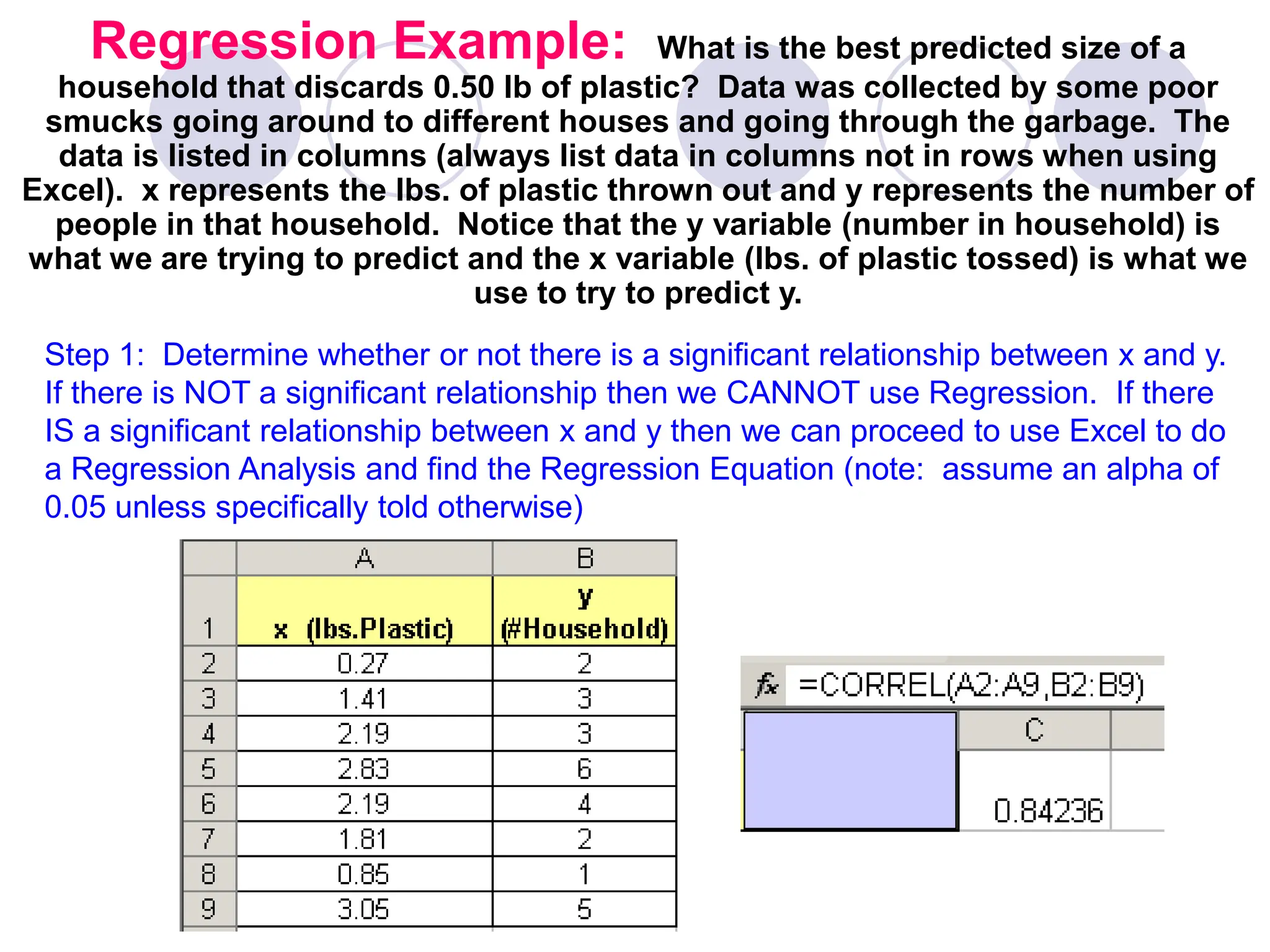
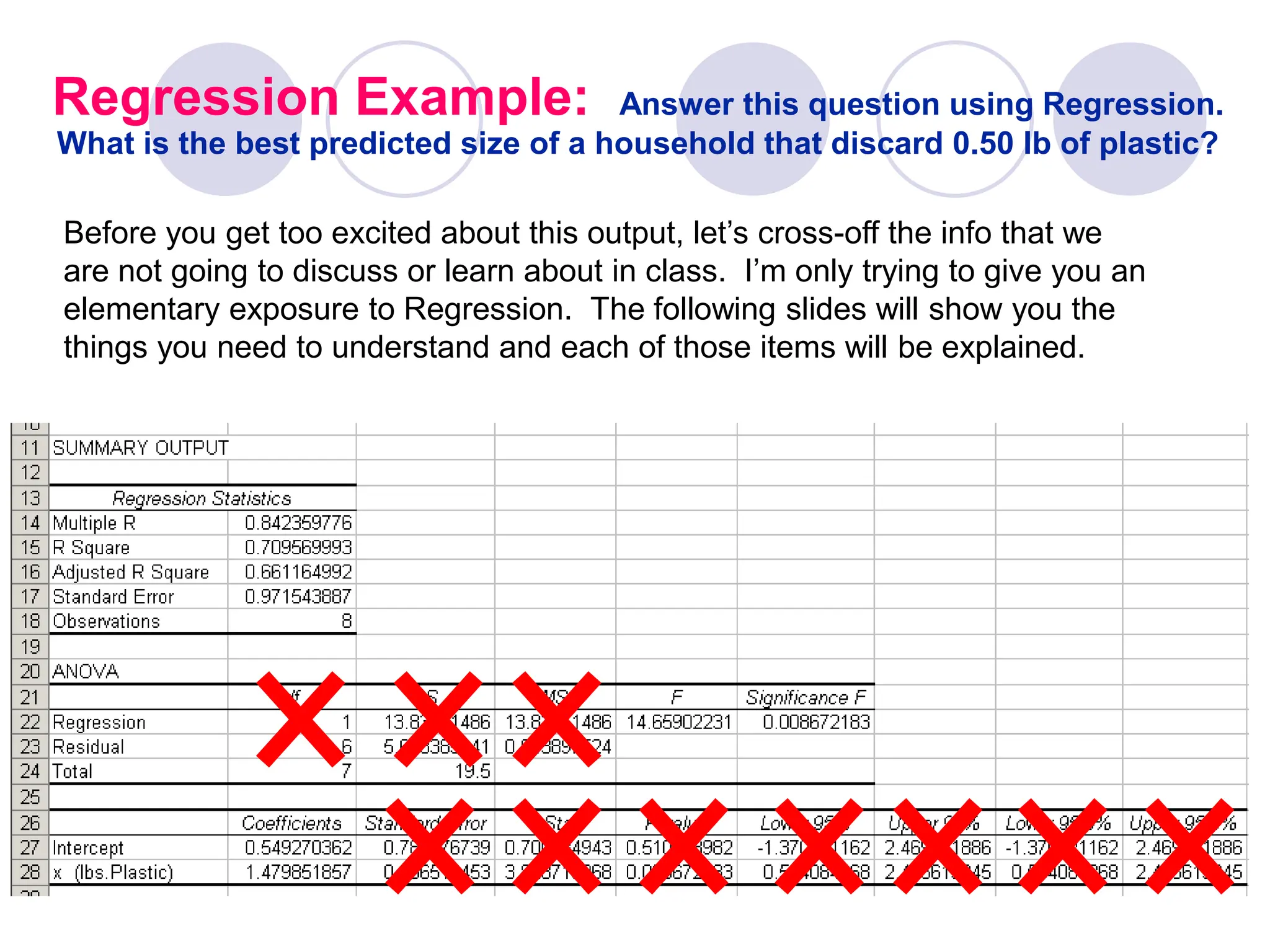
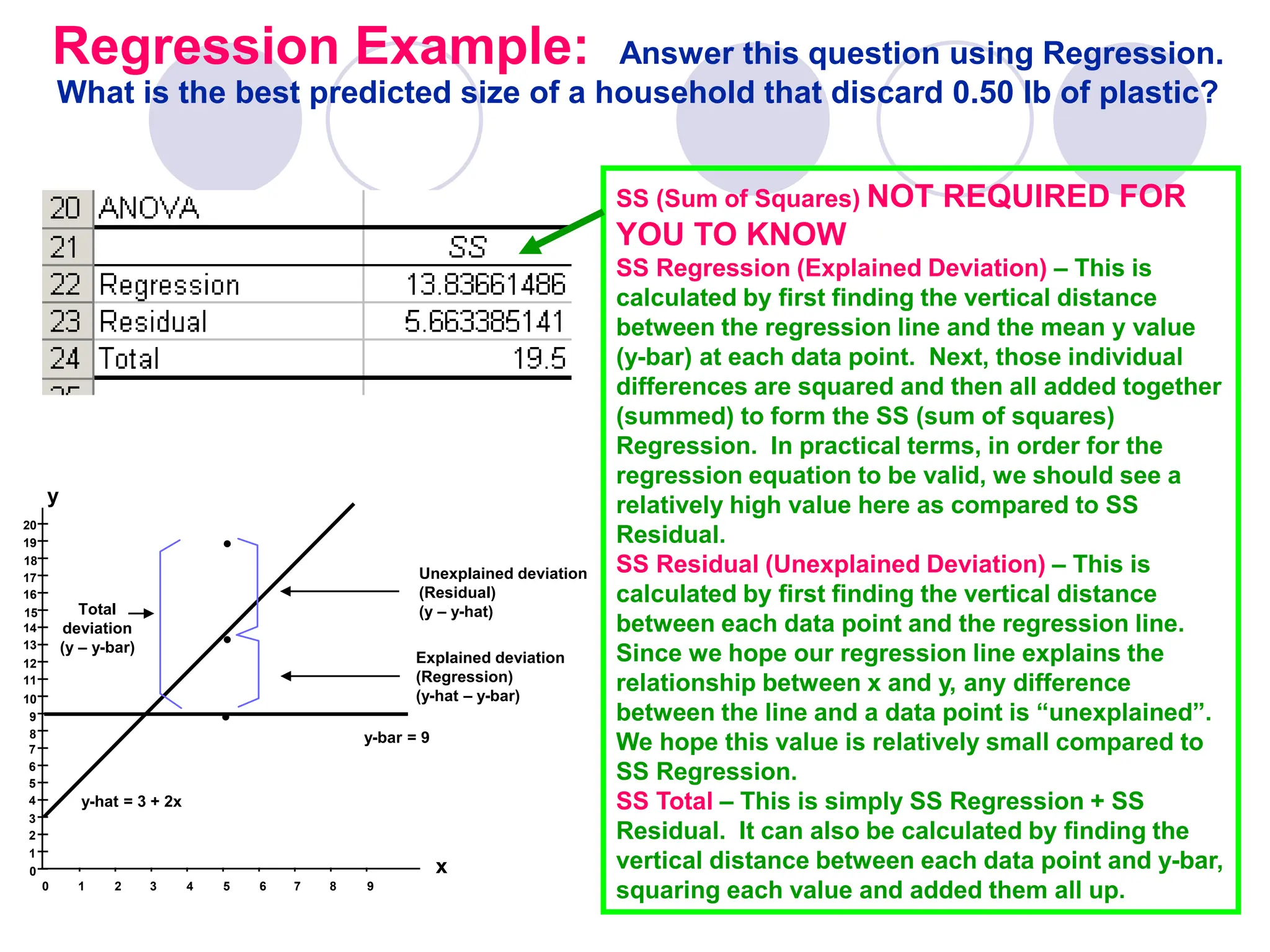
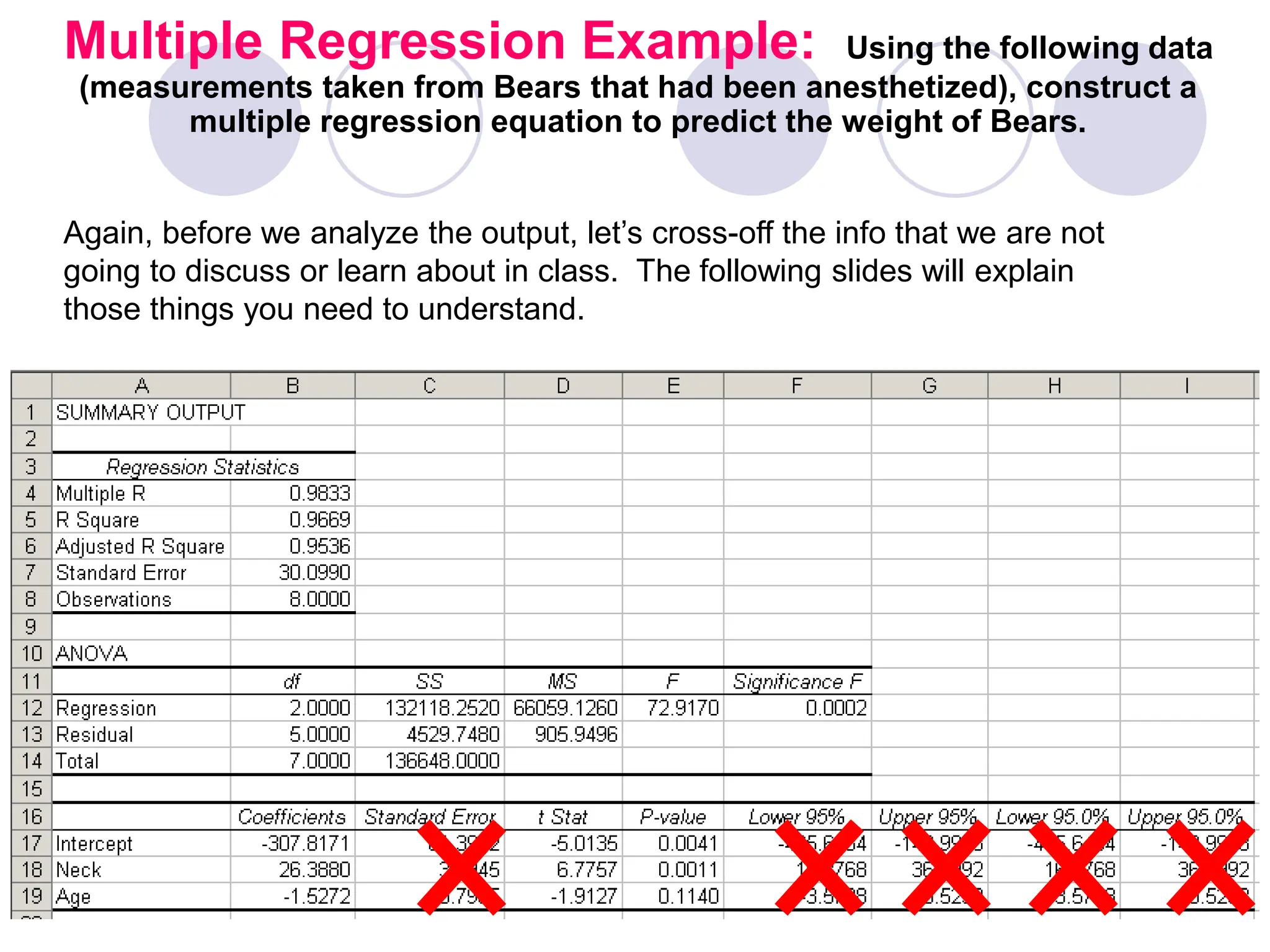
This document provides information on correlation and linear regression analysis. It defines correlation as the relationship between two variables, and discusses positive, negative, and no correlation. Linear regression finds the best-fitting straight line through data points to predict the dependent variable from the independent variable. The key aspects are:
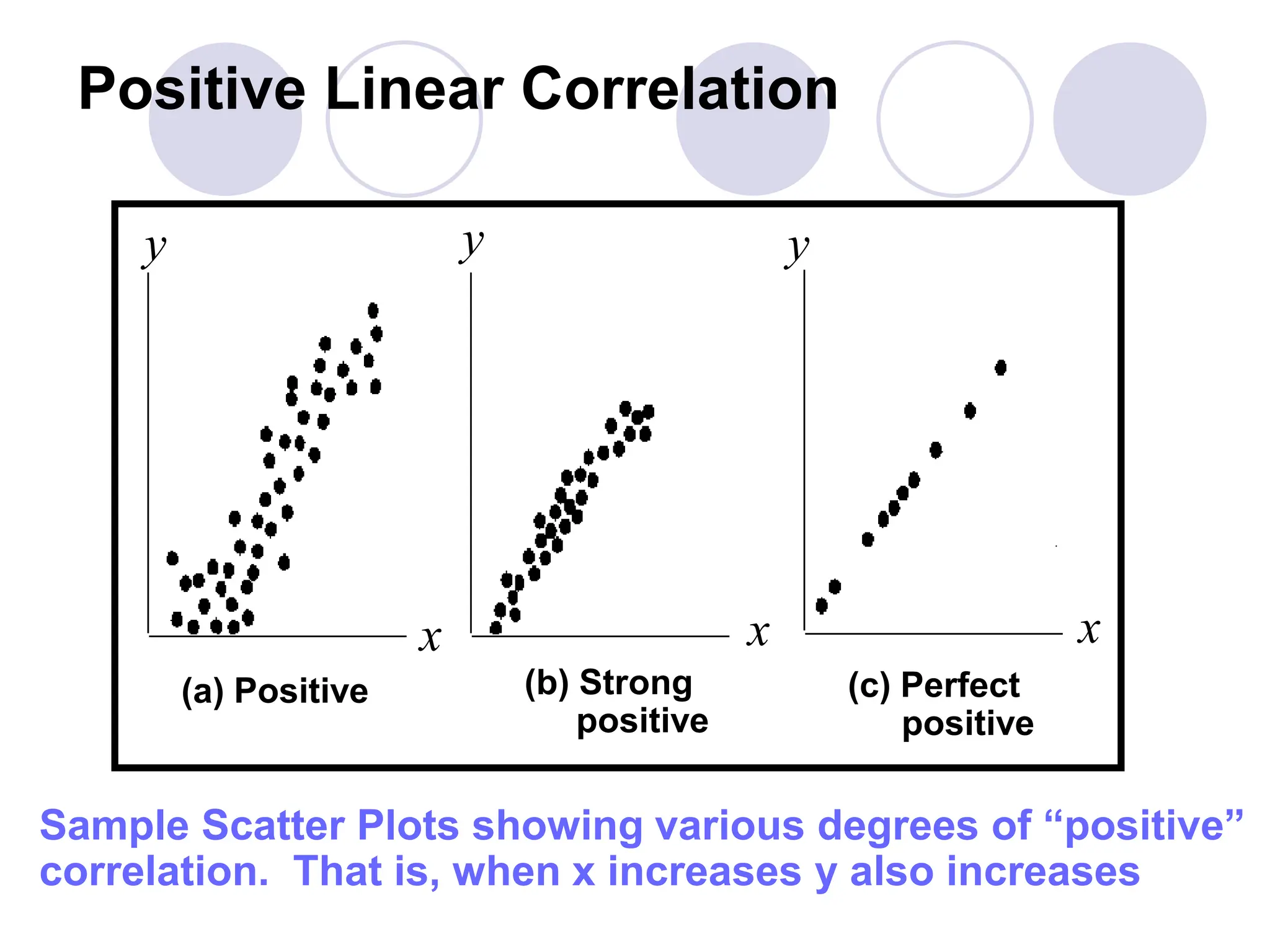
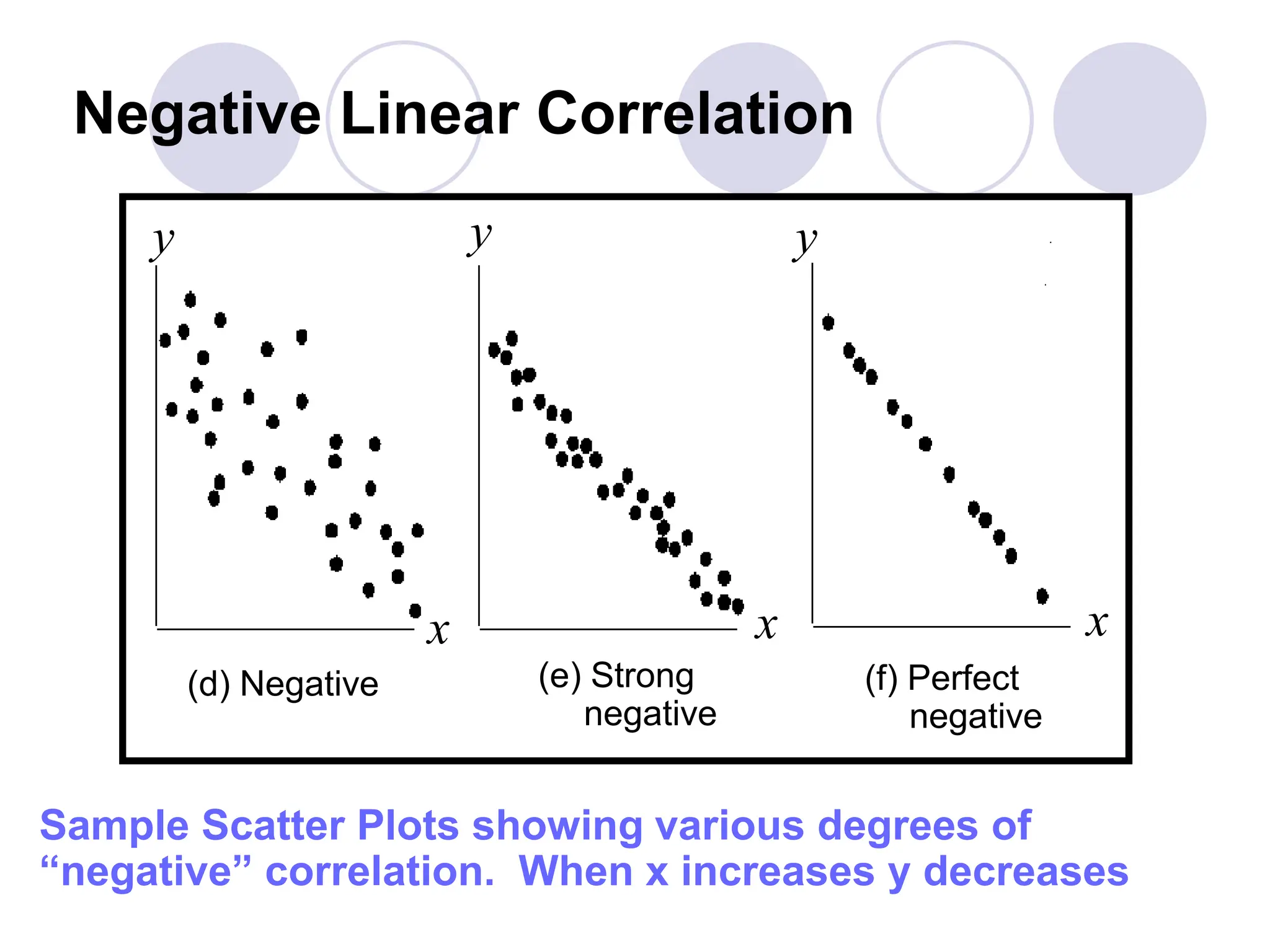
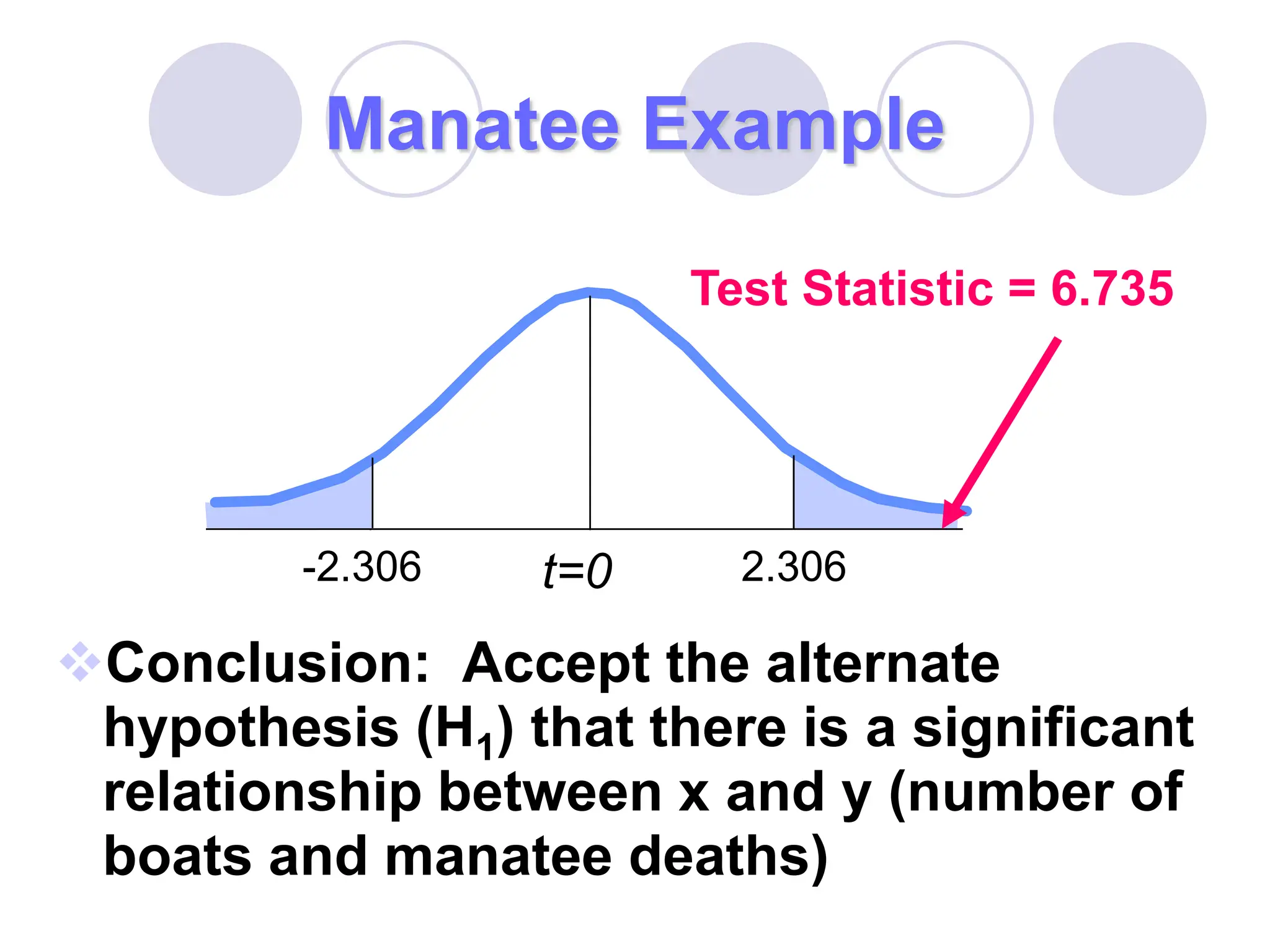
- Correlation is measured by r, which ranges from -1 to 1, with values farther from 0 indicating stronger correlation.
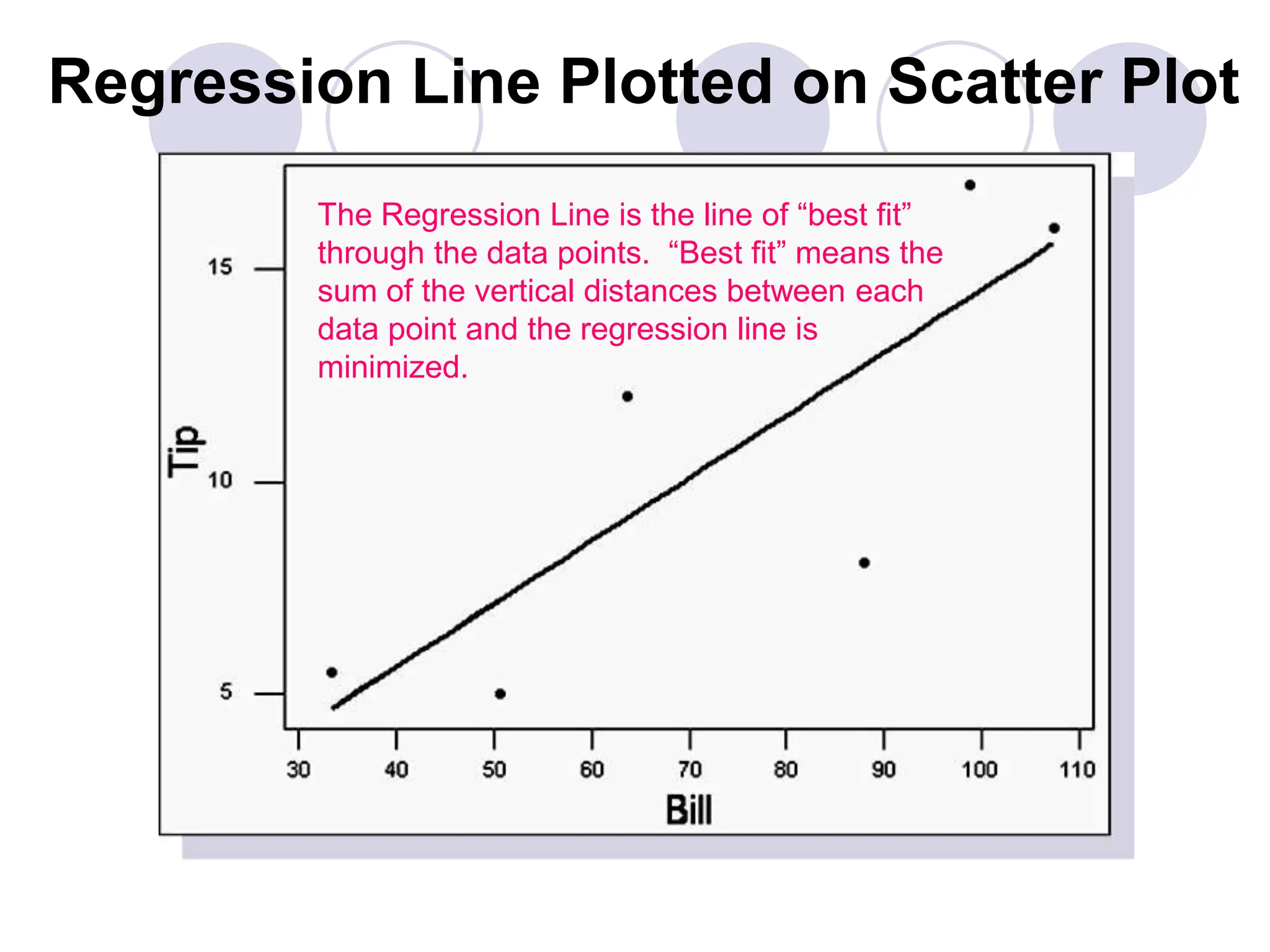
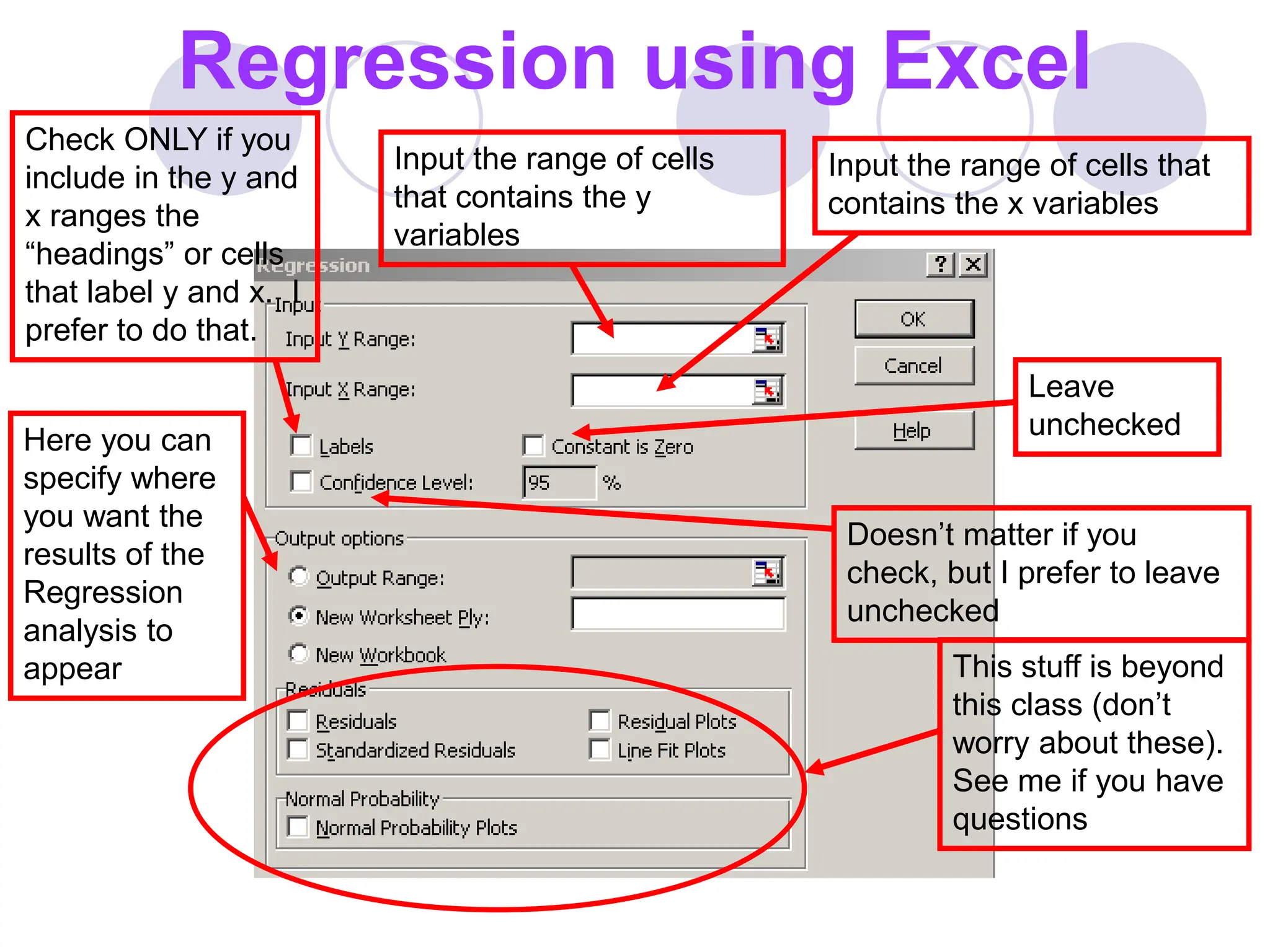
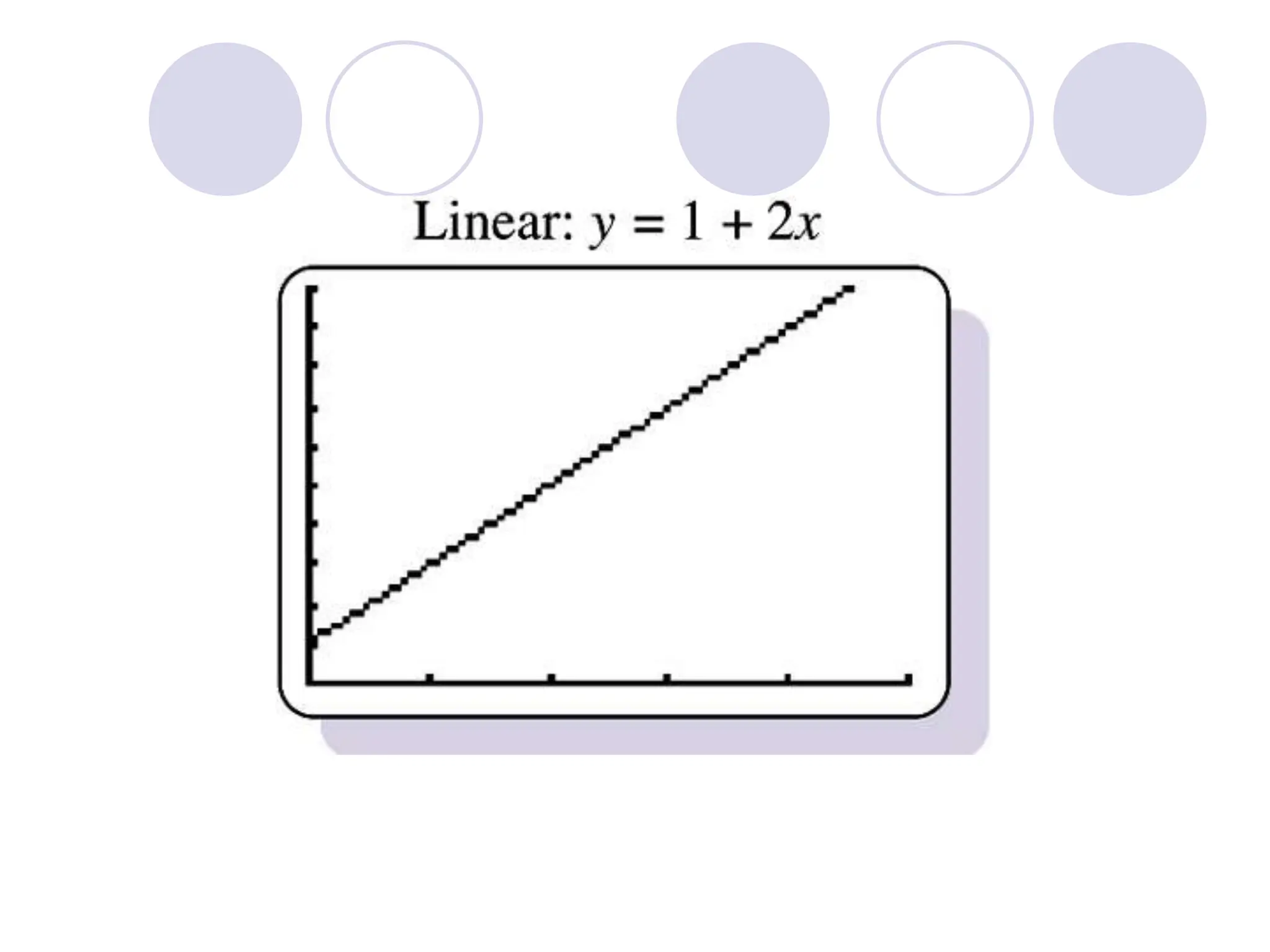
- Regression finds the equation of the best-fitting line to predict y from x as y=b0+b1x.
- Assumptions are a linear relationship and normally distributed, equal variance y values for each x.
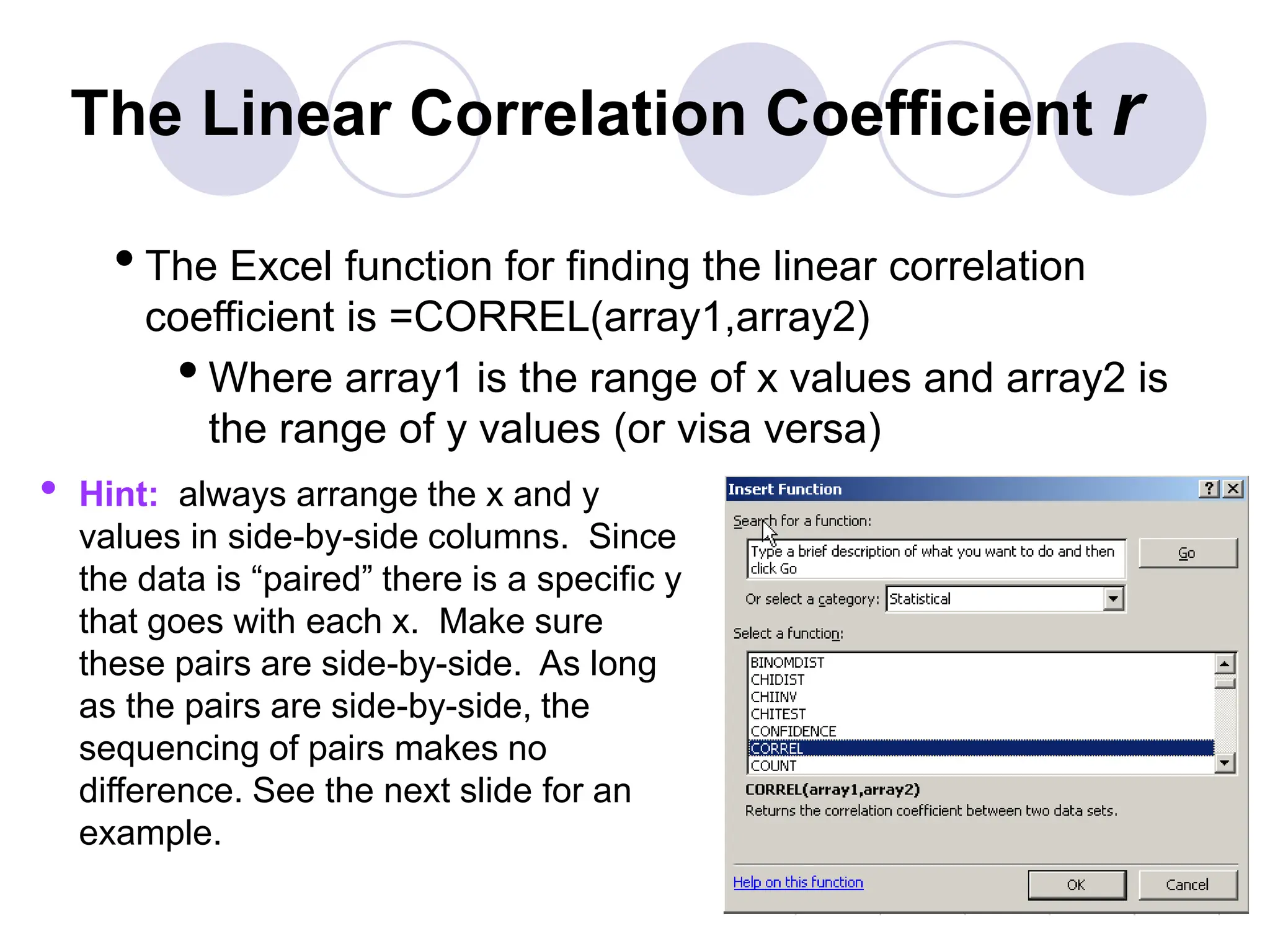
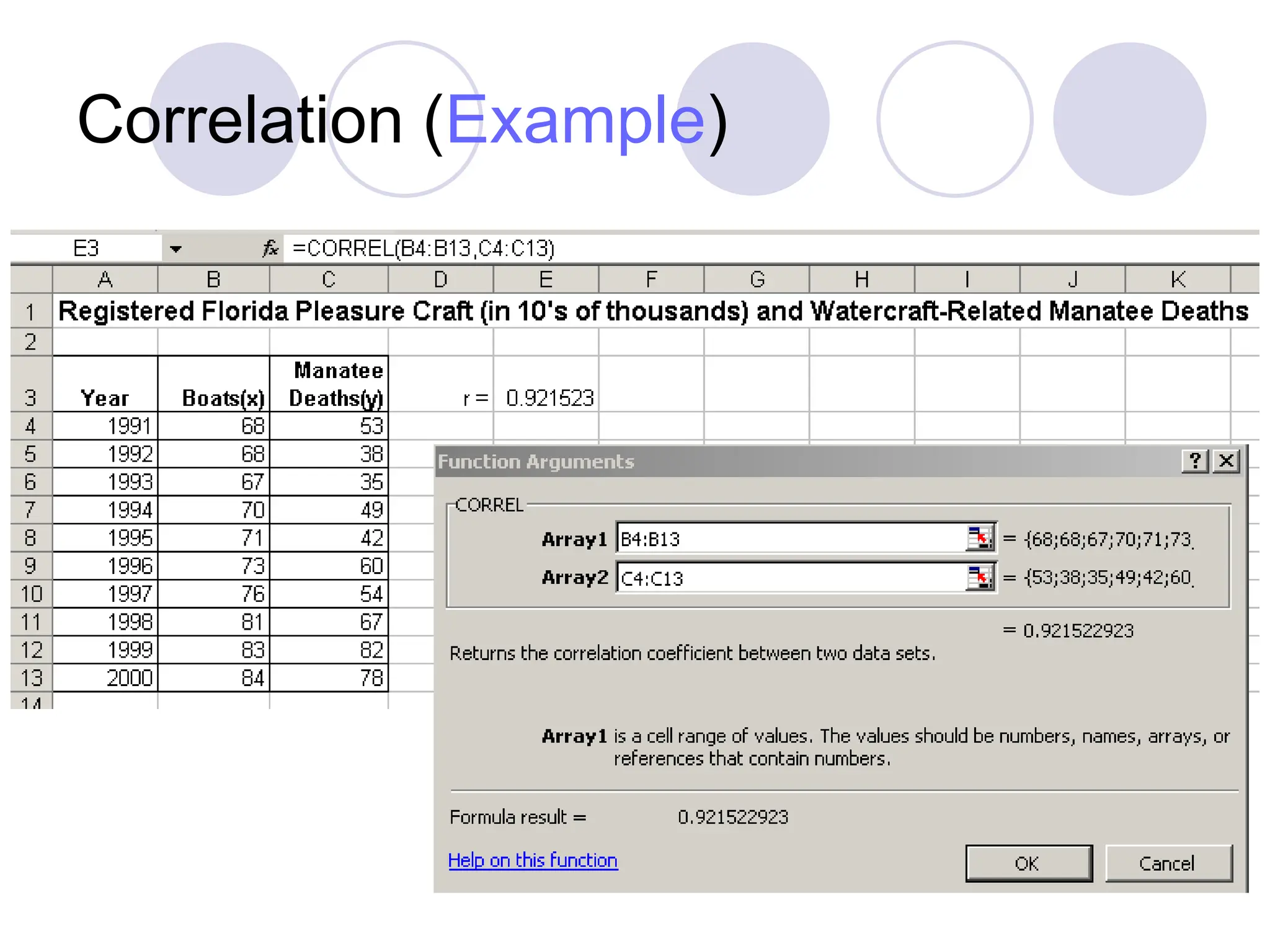
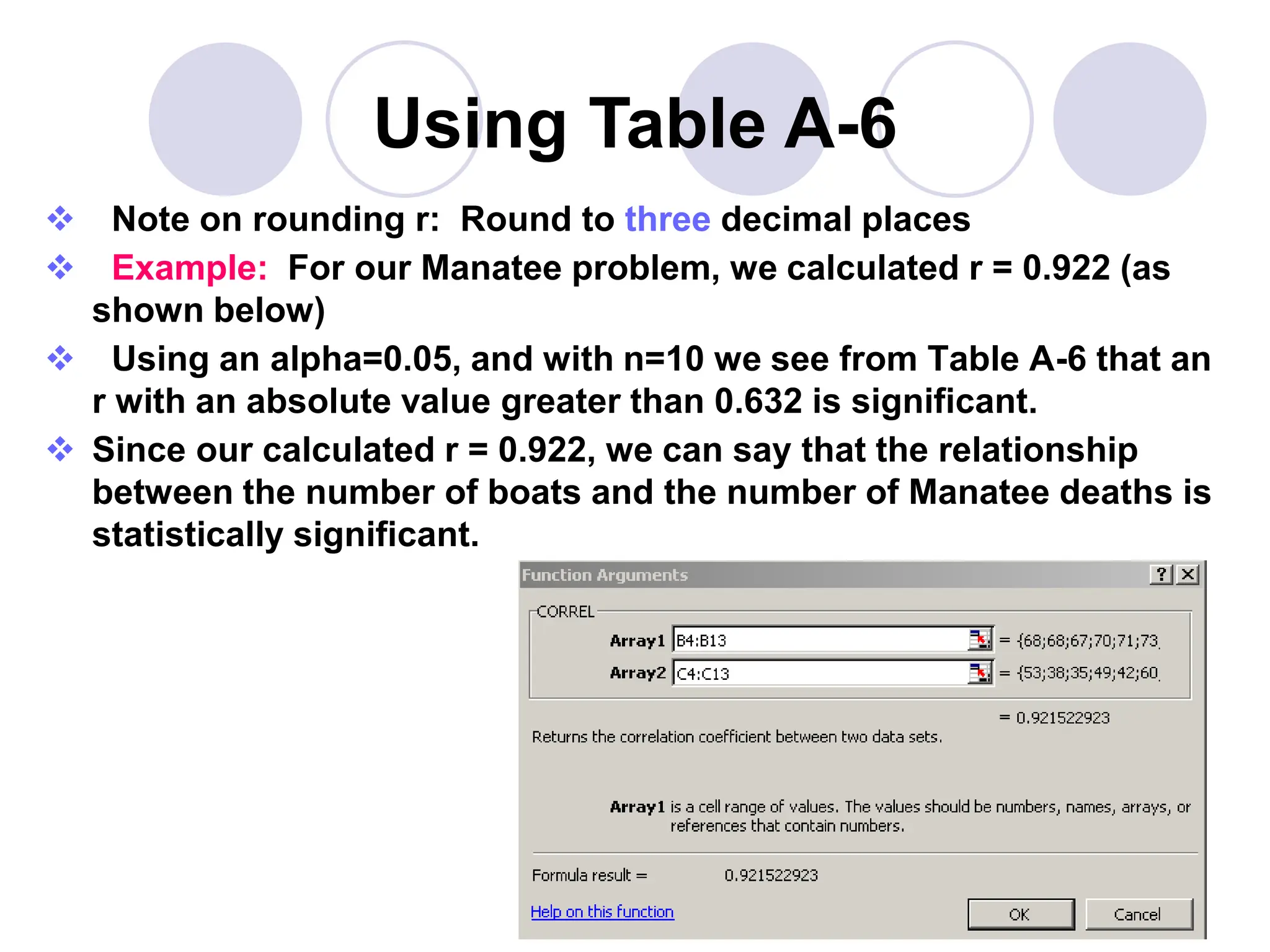
- Excel's CORREL function calculates r and the