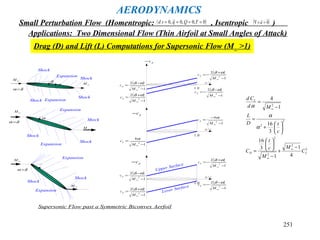
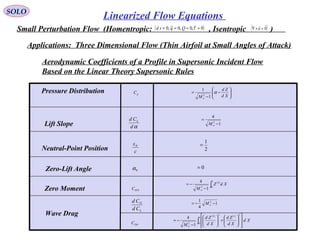
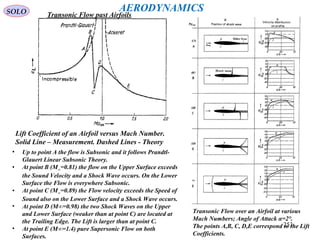
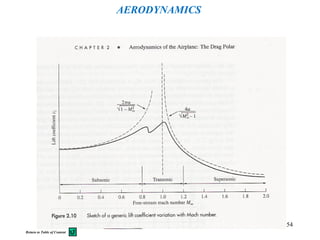
This document provides a table of contents for topics in fluid dynamics. It begins with mathematical notations for vectors, tensors, divergence, gradient, and other vector calculus topics. It then outlines the basic laws of fluid dynamics, such as conservation of mass and momentum. Later sections cover specific fluid dynamics concepts like boundary layers, compressible flow, shock waves, and potential flow. The document provides the framework for equations and analyses of fluid flows.

1. 1
Fluid Dynamics
SOLO HERMELIN
http://www.solohermelin.com

2. SOLO FLUID DYNAMICS
Table of Content
Mathematical Notations
Basic Laws in Fluid Dynamics
1. Conservation of Mass (C.M.)
2. Conservation of Linear Momentum (C.L.M.)
3. Conservation of Moment-of- Momentum (C.M.M.)
4. Conservation of Energy (C.E.), The First Law of Thermodynamics
5. The Second Law of Thermodynamics and Entropy Production
6. Constitutive Relations for Gases
Newtonian Fluid Definitions – Navier–Stokes Equations
State Equation
Thermally Perfect Gas and Calorically Perfect Gas
Boundary Conditions
Dimensionless Equations
Mach Number – Flow Regimes
Boundary Layer and Reynolds Number

3. SOLO FLUID DYNAMICS
Table of Content (continue – 1)
Steady Quasi One-Dimensional Flow
Shock and Expansion Waves
Normal Shock Waves
Flow Description
Streamlines, Streaklines, and Pathlines
Circulation
Biot-Savart Formula
Helmholtz Vortex Theorems
2-D Inviscid Incompressible Flow
Stream Function ψ, Velocity Potential φ in 2-D Incompressible Irrotational
Flow
Blasius Theorem
Kutta Condition
Kutta-Joukovsky Theorem
Joukovsky Airfoils
Shock Wave Definition
Oblique Shock Wave
Prandtl-Meyer Expansion Waves

4. SOLO FLUID DYNAMICS
Table of Content (continue – 2)
Linearized Flow Equations
Cylindrical Coordinates
Small Perturbation Flow
Applications: Three Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Drag (d) and Lift (l) per Unit Span Computations for Subsonic Flow (M∞ < 1)
Prandtl-Glauert Compressibility Correction
Computations for Supersonic Flow (M∞ >1)
Ackeret Compressibility Correction
References

5. 5
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS
VECTOR NOTATION CARTESIAN TENSOR NOTATION
1.1 VECTOR
1.2 SCALAR PRODUCT
1.3 VECTOR PRODUCT
u kk = 1 2 3, ,
   
u u e u e u e= + +1 1 2 2 3 3
 
u v u v u v u v⋅ = + +1 1 2 2 3 3 u v kk k = 1 2 3, ,
 
u v
u u
u u
u u
v
v
v
× =
−
−
−




















0
0
0
3 2
3 1
2 1
1
2
3





=



−
+
±
=−=
ji
permutjiodd
permutjieven
CevittaLevi
vu
ij
jiij
0
.,
.,
1
ε
ε
SOLO

6. 6
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
1.5 ROTOR OF A VECTOR
1.4 DIVERGENCE OF A VECTOR
1.6 GRADIENT OF A SCALAR
∇⋅ = + +

u
u
x
u
x
u
x
∂
∂
∂
∂
∂
∂
1
1
2
2
3
3 i
i
x
u
∂
∂
∇× = −





 + −






+ −






  

u
u
x
u
x
e
u
x
u
x
e
u
x
u
x
e
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
3
2
2
3
1
1
3
3
1
2
1
2
2
1
3
   
u u
u
u u×∇× =∇





 − ⋅∇
2
2
∂
∂
∂
∂
u
x
u
x
i
k
k
i
−
i
k
j
k
i
i
x
u
u
x
u
u
∂
∂
∂
∂
−
∇ = + +
=













φ
∂ φ
∂
∂ φ
∂
∂ φ
∂
∂ φ
∂
∂ φ
∂
∂ φ
∂
x
e
x
e
x
e
x x x
1
1
2
2
31
3
1 2 3
  
∂ φ
∂ xk
SOLO

7. 7
FLUID DYNAMICS
1.MATHEMATICAL NOTATIONS (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
1.7GRADIENT OF A VECTOR
∇ = ∇ + ∇ + ∇
   
u u e u e u e1 1 2 2 3 3
∇ =



















u
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
1
1
1
2
1
3
2
1
2
2
2
3
3
1
3
2
3
3
∇ =
+ + +
+ + +
+ + +



















 
u
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
D
ik
1
2
1
1
1
1
1
2
2
1
1
3
3
1
2
1
1
2
2
2
2
2
2
3
3
1
3
1
1
3
3
2
2
3
3
3
3
3
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂

+
  
ik
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
Ω




















−−
−−
−−
+
0
0
0
2
1
3
2
2
3
3
1
1
3
1
3
3
2
2
1
1
2
1
3
3
1
1
2
2
1
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
u
x
i
k
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
u
x
u
x
u
x
u
x
u
x
i
k
i
k
k
i
i
k
k
i
= +





 + −






1
2
1
2
D
u
x
u
x
ik
i
k
k
i
= +






∆ 1
2
∂
∂
∂
∂
Ω
∆
ik
i
k
k
i
u
x
u
x
= −






1
2
∂
∂
∂
∂
SOLO

8. 8
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
1.8 GAUSS’ THEOREMS
ds
A
V
∇⋅

A analytic in V
↓ = =
  
A C C const vectorη .
( ) ∫∫ ∫∫∫∇=
S V
dvsdGAUSS ηη

2
∇ηanalytic in V ∫∫ ∫∫∫=
S k
k
V
dv
s
ds
∂
η∂
η
SOLO
Johann Carl Friederich Gauss
1777-1855
( ) ∫∫ ∫∫∫ ⋅∇=⋅
S
V
dvAsdAGAUSS

1
∫∫ ∫∫∫=
S k
k
kk
V
dv
x
A
dsA
∂
∂

9. 9
FLUID DYNAMICS
1.MATHEMATICAL NOTATIONS (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
1.8GAUSS’ THEOREMS (CONTINUE)
( ) ( ) ( )∫∫ ∫∫∫ ⋅∇=⋅
S V
dvAsdAGAUSS

ηη3
( )= ⋅∇ + ∇⋅∫∫∫
 
A A dvη η
η∇⋅∇ ,A

analytic inV
( )η
∂ η
∂
A ds
A
x
dv
V
k k
k
kS
= ∫∫∫∫∫
∫∫∫ 





+=
V k
k
k
k
x
A
x
A
∂
∂
η
∂
η∂
↓ = + +
   
B e e eη η η1 1 2 2 3 3
( ) ( ) ( )[ ]∫∫ ∫∫∫ ⋅∇+∇⋅=⋅
S V
dvABBAsdABGAUSS

4 B A ds A
B
x
B
A
x
dv
V
i k k k
i
k
i
k
kS
= +





∫∫∫∫∫
∂
∂
∂
∂
∇ ×

A analytic inV( ) ∫∫ ∫∫∫ ×∇=×
S V
dvAAsdGAUSS

5 ( )ds A ds A
A
x
A
x
dv
V
i j j i
j
i
i
jS
− = −





∫∫∫∫∫
∂
∂
∂
∂
SOLO

10. 10
FLUID DYNAMICS
1.MATHEMATICAL NOTATIONS (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
1.9STOCKES’ THEOREM
   
A d r A d s
C S
⋅ = ∇ × ⋅∫ ∫∫ ∇ ×

A analytic on S
A d r
A
x
A
x
d si i
C
j
i
i
j
k
S
∫ ∫∫= −






∂
∂
∂
∂
Gauss’ and Stokes’ Theorems are generalizations of the
Fundamental Theorem Of CALCULUS
( )A b A a
d A x
d x
d x
a
b
( ) ( )− = ∫
George Stokes
1819-1903
SOLO

11. 11
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS
VECTOR NOTATION CARTESIAN TENSOR NOTATION
MATERIAL DERIVATIVES (M.D.)
1
e
2e
3
e
r

u

b

rd
( )d F r t
F
t
dt dr F
 

 
, = + ⋅∇
∂
∂
( )
d
dt
F r t
F
t
dr
dt
F
 
 

, = + ⋅∇
∂
∂
( )
d
dt
F r t
F
t
b F
b
 

 
, = + ⋅∇
∂
∂
forany dr
 ( )d F r t
F
t
dt d r
F
x
i k
i
k
i
k
, = +
∂
∂
∂
∂
( )
d
dt
F r t
F
t
d r
dt
F
x
i k
i k i
k
, = +
∂
∂
∂
∂
( )
d
dt
F r t
F
t
b
F
xb
i k
i
k
i
k
, = +
∂
∂
∂
∂
vectoranybbtd
rd

=
Joseph-Louis
Lagrange
1736-1813
Leonhard Euler
1707-1783
SOLO
FIXED IN SPACE
(CONSTANT VOLUME)
EULER
LAGRANGE
MOVING WITH THE FLUID
(CONSTANT MASS)
1e
3
e
2e
u

12. 12
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
MATERIAL DERIVATIVES (CONTINUE)
( ) Fu
t
F
F
tD
D
trF
td
d
u



∇⋅+=≡
∂
∂
,
( )
k
i
k
i
ki
u x
F
u
t
F
F
tD
D
trF
td
d
∂
∂
∂
∂
+=≡,velocityfluiduu
td
rd
If


=
Material Derivatives
=
Derivative Along A Fluid Path (Streamline)
D
D t
u
u
t
u u
u
t
u
u u


 

 
= + ⋅∇
= + ∇





 − × ∇ ×
∂
∂
∂
∂
2
2
1e
2
e
3e
r

u
 duu +

dr
Acceleration
Of The Fluid






⋅−⋅−






+=
+=
k
i
k
i
j
j
j
i
i
k
i
k
i
i
x
u
u
x
u
u
u
xt
u
x
u
u
t
u
u
tD
D
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
2
2
1
SOLO

13. 13
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
1.10 MATERIAL DERIVATIVES (CONTINUE)
d u
u
t
dt dr u


 
= + ⋅∇
∂
∂
du
u
t
dt dx
u
x
i
i
k
i
k
= + ⋅
∂
∂
∂
∂
rdrdDtd
t
u
xd
xd
xd
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
x
u
t
u
t
u
t
u
ud
ud
ud
ikik


Ω++=




























+


















=










∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
3
2
1
3
3
2
3
1
3
3
2
2
2
1
2
3
1
2
1
1
1
3
2
1
3
2
1

d u
u
t
d t
u
x
u
x
d x
u
x
u
x
d x
i
i
Translation
i
k
k
i
Dilation
k
i
k
k
i
Rotation
k
= +
+ +






+ −






∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
1
2
1
2
  
  ( )
( )
( )
( )[ ] Dilationrduu
rdurdu
urdrdurdu
rdurdurdD
T
u
u
ik
⇒⋅∇+∇=
⋅∇+⋅∇=
∇⋅−⋅∇+⋅∇=
××∇−⋅∇=




2
1
2
1
2
1
2
1
2
1
2
1
( )Ωik dr u dr Rotation
  
= ∇ × × ⇒
1
2
SOLO

14. 14
REYNOLDS’ TRANSPORT THEOREM
-any system of coordinatesOxyz
- any continuous and differentiable
functions in
( ) ( )trtr OO ,,, ,,

ηχ
( )tandrO,

( )trO ,,

ρ - flow density at point
and time t
Or,

SOLO
- mass flow through the element .mdsdVS


=⋅− ,ρ sd

- any control volume, changing shape, bounded by a closed surface S(t)v (t)
- flow velocity, relative to O, at point and time t( )trV OOflow ,,,

Or,

- position and velocity, relative to O, of an element of surface, part of the
control surface S(t).
OSOS Vr ,, ,

- area of the opening i, in the control surface S(t).iopenS
- gradient operator in O frame.O,∇
- flow relative to the opening i, in the control surface S(t).OSiOflowSi VVV ,,,

−=
- differential of any vector , in O frame.
O
td
d ζ

ζ

FLUID DYNAMICS

15. 15
Start with LEIBNIZ THEOREM from CALCULUS:
( ) ( )
  
ChangeBoundariesthetodueChange
tb
ta
tb
ta td
tad
ttaf
td
tbd
ttbfdx
t
txf
dxtxf
td
d
LEIBNITZ 





−+= ∫∫ )),(()),((
),(
),(::
)(
)(
)(
)( ∂
∂
and generalized it for a 3 dimensional vector space on a volume v(t) bounded by the
surface S(t).
Using LEIBNIZ THEOREM followed by GAUSS THEOREM (GAUSS 4):
( ) ( )
( ) ( )
∫∫∫∫∫ 





⋅∇+∇⋅+=⋅+
→
=
tv
OSOOOSGAUSS
Opotolative
dsofMovement
thetodueChage
tS
OS
tv
O
LEIBNITZ
O
tv
vdVV
t
GAUSS
sdVvd
t
vd
td
d
,,,,)4(
intRe
)(
,





χχ
∂
χ∂
χ
∂
χ∂
χ
This is REYNOLDS’ TRANSPORT THEOREM
OSBORNE
REYNOLDS
1842-1912
SOLO
GOTTFRIED WILHELM
von LEIBNIZ
1646-1716
REYNOLDS’ TRANSPORT THEOREM
FLUID DYNAMICS
1.MATHEMATICAL NOTATIONS (CONTINUE)

16. 16
FLUID DYNAMICS
1.MATHEMATICAL NOTATIONS (CONTINUE)
1.11REYNOLDS’ TRANSPORT THEOREM (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
( )
∫∫∫
∫∫∫∫∫∫∫∫








⋅∇+∇⋅+=
⋅+=
)(
,,,,)4(
,
)()()(
tv
OSOOOS
O
GAUSS
OS
tStv
O
LEIBNITZ
O
tv
vdVV
t
GAUSS
sdVvd
t
vd
td
d




χχ
∂
χ∂
χ
∂
χ∂
χ
∫∫∫
∫∫∫∫∫∫∫∫








++=
+=
)(
,
,)4(
,
)()()(
tv k
kOS
i
k
i
kOS
i
GAUSS
kkOS
tS
i
tv
i
LEIBNITZ
tv
i
vd
x
V
x
V
t
GAUSS
sdVvd
t
vd
td
d
∂
∂
χ
∂
χ∂
∂
χ∂
χ
∂
χ∂
χ
SOLO

17. 17
FLUID DYNAMICS
1.MATHEMATICAL NOTATIONS (CONTINUE)
1.11REYNOLDS’ TRANSPORT THEOREM (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
O
OOS
td
Rd
uV


== ,,
CASE 1 (CONTROL VOLUME vF ATTACHED TO THE FLUID)
kkOS
uV =,
( )
∫∫∫
∫∫∫∫∫∫∫∫








⋅∇+∇⋅+=
⋅+=
)(
,,,)4(
,
)()()(
tv
OOO
O
GAUSS
O
tStv
OO
tv
F
FFF
vduu
t
GAUSS
sduvd
t
vd
td
d





χχ
∂
χ∂
χ
∂
χ∂
χ
∫∫∫
∫∫∫∫∫∫∫∫








++=
+=
)(
)4(
)()()(
tv k
k
I
k
I
k
I
GAUSS
kK
tS
I
tv
I
tv
I
F
FFF
vd
x
u
x
u
t
GAUSS
sduvd
t
vd
td
d
∂
∂
χ
∂
χ∂
∂
χ∂
χ
∂
χ∂
χ
SOLO

18. 18
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS (CONTINUE)
1.11 REYNOLDS’ TRANSPORT THEOREM (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
1&,
== χkkOS
uV1&, == χuV OS

CASE 2 (CONTROL VOLUME vF ATTACHED TO THE FLUID AND )1=χ
∫∫∫∫∫∫∫∫ ⋅∇=⋅==
)(
,,
)(
,
)(
)(
tv
OO
tS
O
tv
F
FFF
vdusduvd
td
d
td
tvd 
∫∫∫∫∫∫∫∫ ===
)()()(
)(
tv k
k
k
tS
k
tv
F
FFF
dv
x
u
dsudv
td
d
td
tvd
∂
∂














=⋅∇
→ td
tvd
tv
u F
F
tv
OO
F
)(
)(
1
lim0)(
,,















=
→ td
tvd
tvx
u F
F
tv
k
k
F
)(
)(
1
lim0)(∂
∂
EULER 1755
SOLO

19. 19
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS (CONTINUE)
1.11 REYNOLDS’ TRANSPORT THEOREM (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
CASE 3 (CONTROL VOLUME vF ATTACHED TO THE FLUID AND )
ρχ == &, kkOS uVρχ == &, uV OS

ρχ =
or, since this is true for any attached volume vF(t)
( )∫∫∫
∫∫∫∫∫ ∫∫∫






⋅∇+=
⋅+===
)(
,,
)(
,
)( )(
)(
0
tv
OO
tS
O
tv tv
F
FF F
vdu
t
sduvd
t
vd
td
d
td
tmd


ρ
∂
ρ∂
ρ
∂
ρ∂
ρ
( )∫∫∫
∫∫∫∫∫ ∫∫∫






+=
+===
)(
)()( )(
)(
0
tv
k
k
tS
kk
tv tv
F
FF F
vdu
xt
sduvd
t
dv
td
d
td
tmd
ρ
∂
∂
∂
ρ∂
ρ
∂
ρ∂
ρ
Because the Control Volume vF is attached to the fluid and they are not sources or sinks,
the mass is constant.
( ) OOOOOO uu
t
u
t
,,,,,,0

⋅∇+∇⋅+=⋅∇+= ρρ
∂
ρ∂
ρ
∂
ρ∂
( )
k
k
k
k
k
x
u
x
u
t
u
xt ∂
∂
ρ
∂
ρ∂
∂
ρ∂
ρ
∂
∂
∂
ρ∂
++=+=

0
SOLO

20. 20
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS (CONTINUE)
1.11 REYNOLDS’ TRANSPORT THEOREM (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
CASE 4 (CONTROL VOLUME WITH FIXED SHAPE C.V. )0,

=OS
V
Define
∫∫∫∫∫∫ =
.... VC
OO
VC
vd
t
vd
td
d
∂
χ∂
χ


∫∫∫∫∫∫ =
.... VC
i
VC
i vd
t
vd
td
d
∂
χ∂
χ
( ) ( ) ( )
    
χ ρ ηr t r t r t, , ,≡ ( ) ( ) ( )χ ρ ηi k k i kx t x t x t, , ,≡
( )∫∫
∫∫∫∫∫∫
⋅+








+=
)(
,
)()(
tS
OS
tv
OO
tv
sdV
vd
tt
vd
td
d




ηρ
∂
ρ∂
η
∂
η∂
ρηρ
k
tS
kOSi
tv
i
i
tv
i
sdV
vd
tt
vd
td
d
FF
∫∫
∫∫∫∫∫∫
+






+=
)(
,
)()(
ηρ
∂
ρ∂
η
∂
η∂
ρηρ
We have
but
( ) ( )OOOO
u
t
u
t
,,,,
0

ρη
∂
ρ∂
ηρ
∂
ρ∂
⋅∇−=⇒=⋅∇+
( ) ( )k
k
iik
k
u
xt
u
xt
ρ
∂
∂
η
∂
ρ∂
ηρ
∂
∂
∂
ρ∂
−=⇒=+ 0
CASE 5 ( ) ( ) ( )    
χ ρ ηr t r t r t, , ,≡
SOLO

21. 21
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS (CONTINUE)
1.11 REYNOLDS’ TRANSPORT THEOREM (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
We have
( )
( )
( ) ( )[ ]
( )
( )[ ]∫∫∫∫∫=
∫∫
∫∫∫
∫∫
∫∫∫∫∫∫
⋅−+
⋅+








⋅∇+∇⋅−








∇⋅+=
⋅+








⋅∇−=
+
+
)(
,,
)(
4
.
)(
,
)(
,,,,,,
)(
,
)(
,,
)(
tS
OOS
tv
O
MDG
DerMat
GAUSS
tS
OS
tv
OOOOOO
O
tS
OS
tv
OO
OO
tv
sduVvd
tD
D
sdV
vduuu
t
sdV
vdu
t
vd
td
d









ρηρ
η
ρη
ρηηρη
∂
η∂
ρ
ρη
ρηρ
∂
η∂
ρη ( )
( )
( ) ( )
( )
( )[ ]∫∫∫∫∫=
∫∫
∫∫∫
∫∫
∫∫∫∫∫∫
−+
+














+−





+=
+






−=
+
+
)(
,
)(
4
.
)(
,
)(
)(
,
)()(
tS
kkkOSi
tv
i
MDG
DerMat
GAUSS
tS
kkOSi
tv k
k
i
k
i
k
k
i
k
i
tS
kkOSi
tv k
k
i
i
tv
i
sduVvd
tD
D
sdV
vd
x
u
x
u
x
u
t
sdV
vd
x
u
t
vd
td
d
ρηρ
η
ρη
∂
ρ∂
η
∂
η∂
ρ
∂
η∂
∂
η∂
ρ
ρη
∂
ρ∂
ηρ
∂
η∂
ρη
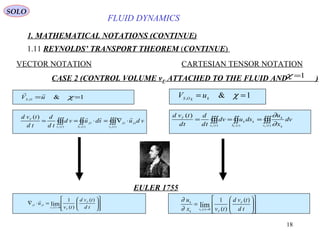
CASE 5 ( ) ( ) ( )    
χ ρ ηr t r t r t, , ,≡
SOLO

22. 22
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS (CONTINUE)
1.11 REYNOLDS’ TRANSPORT THEOREM (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
REYNOLDS 1
( )[ ]






⋅−+= ∫∫∫∫∫
∫∫∫
)(
,,
)(
)(
tS
OOS
tv
O
O
tv
sduVvd
tD
D
vd
td
d



ρηρ
η
ρη
( )[ ]






−+= ∫∫∫∫∫
∫∫∫
)(
,
)(
)(
tS
kkkOSi
tv
i
tv
i
sduVvd
tD
D
dv
td
d
ρηρ
η
ρη
REYNOLDS 2
( )[ ]







=
⋅−+
∫∫∫
∫∫∫∫∫
)(
)(
,,
)(
tv
O
tS
OSO
O
tv
vd
tD
D
sdVuvd
td
d
ρ
η
ρηρη


( )[ ]







=
−+
∫∫∫
∫∫∫∫∫
)(
)(
,
)(
tv
i
tS
kkOSki
tv
i
vd
tD
D
sdVuvd
td
d
ρ
η
ρηρη
CASE 5 ( ) ( ) ( )
    
χ ρ ηr t r t r t, , ,≡
SOLO

23. 23
FLUID DYNAMICS
1. MATHEMATICAL NOTATIONS (CONTINUE)
1.11 REYNOLDS’ TRANSPORT THEOREM (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
REYNOLDS 3
CASE 1 (CONTROL VOLUME ATTACHED TO THE FLUID vF(t) )
kkOS
uV =,
∫∫∫∫∫∫ =
)()( tv
OO
tv FF
vd
tD
D
vd
td
d
ρ
η
ρη


∫∫∫∫∫∫ =
)()( tv
i
tv
i
FF
vd
tD
D
vd
td
d
ρ
η
ρη
SOLO
O
OOS
td
Rd
uV


== ,,
( ) ( ) ( )    
χ ρ ηr t r t r t, , ,≡
CASE 4 (CONTROL VOLUME WITH FIXED SHAPE C.V. )0,

=OS
V
REYNOLDS 4
( )






⋅+= ∫∫∫∫∫
∫∫∫
..
,
..
..
SC
O
O
VC
VC
O
sduvd
td
d
vd
tD
D


ρηρη
ρ
η
( )






+= ∫∫∫∫∫
∫∫∫
....
..
SC
kki
VC
i
VC
i
sduvd
td
d
vd
tD
D
ρηρη
ρ
η
Return to Table of Content

24. 24
BASIC LAWS IN FLUID DYNAMICS
THE FLUID DYNAMICS IS DESCRIBED BY THE FOLLOWING FOUR LAWS:
(1) CONSERVATION OF MASS (C.M.)
(2) CONSERVATION OF LINEAR MOMENTUM (C.L.M.)
(4) THE FIRST LAW OF THERMODYNAMICS
(5) THE SECOND LAW OF THERMODYNAMICS
SOLO
(3) CONSERVATION OF MOMENT-OF-MOMENTUM (C.M.M.)
FLUID DYNAMICS
Return to Table of Content
(6) CONSTITUTIVE RELATIONS

25. 25
BASIC LAWS IN FLUID DYNAMICS
(1)CONSERVATION OF MASS (C.M.)
SOLO
The mass in the Fixed Control Volume (C.V.)
is given by:
∫∫∫=
..VC
CV vdm ρ
Since the mass entering the C.V. is equal to mass
exiting C.V., using Reynolds’ Transport Theorem
with η = 1, we have:
( )∫∫∫∫∫ ⋅−===
..
,
Re
..
0
SC
md
S
ynolds
VC
md
CV
sdVvd
td
d
td
md




ρρ
Assume:
- one inlet (1) of area A1 and mean fluid velocity V,S1 (relative to A1 )and density ρ1.
- one outlet (2) of area A2 and mean fluid velocity V,S2 (relative to A2 ) and density ρ2.
we have: ( ) ( ) ( ) ( ) ( ) 022,21,1,,
.. 21
=−=⋅−+⋅−=⋅− ∫∫∫∫∫∫ AVAVsdVsdVsdV SnSn
A
S
A
S
SC
ρρρρρ

- mass flow rate entering the system through the element of C.S.mdsdVS


=⋅− ,ρ sd

or: ( ) ( )
21
22,211,1
flowflow Q
Sn
Q
Sn AVAV ρρ =
where: - mass flow velocity exiting the system relative to the element of
C.S.
SSflow VV ,,

= sd

FLUID DYNAMICS

26. 26
SOLO
1 2 30 4 5 6
SUPERSONIC
COMPRESSION
SUBSONIC
COMPRESSION
COMBUSTION
FUEL
INJECTION EXPANSION
NOZZLECOMBUSTION
CHAMBER
DIFFUSER
FLAME
HOLDERS
EXHAUST
JET
0V
0A
fm
(1) CONSERVATION OF MASS (C.M.)
2221110000 AuAuAum ρρρ ===
6665554443330 AuAuAuAumm f ρρρρ ====+ 
DiffuserEnteringRateFlowMassAirm −0

RateFlowMassFuelmf −
6,5,4,3,2,1,0,,,,,, 6543210 StationsatDensityGasρρρρρρρ
6,5,4,3,2,1,0,,,,,, 6543210 StationsatVelocityGasuuuuuuu
6,5,4,3,2,1,0,,,,,, 6543210 StationsatAreaAAAAAAA
BASIC LAWS IN FLUID DYNAMICS
FLUID DYNAMICS
Return to Table of Content

27. 27
BASIC LAWS IN FLUID DYNAMICS
(2) CONSERVATION OF LINEAR MOMENTUM (C.L.M.)
SOLO
∫∫∫=
..
:
VC
CCV vdRRm ρ

Using the Reynolds’ Transport Theorem we obtain
The Centroid of the mass enclosed by C.V. isCR

The Linear Moment of the mass enclosed by C.V. is defined as
∫∫∫∫∫∫ ==
....
,
:
VC
I
VC
ICV
vd
tD
RD
vdVP ρρ


( )
( ) ( ) ( ) ( )∫∫∫∫∫∫
∫∫∫∫∫∫∫∫
⋅+⋅−+=⋅+=
⋅+==
..
,
..
,
..
,
..
,
....
SC
S
m
SC
SC
V
I
C
CV
SC
S
I
CCV
SC
S
VC
REYNOLDS
VC
I
CV
sdVRsdVR
td
Rd
msdVRRm
td
d
sdVRvdR
td
d
vd
tD
RD
P
CV
C

  








ρρρ
ρρρ
( ) ( )∫∫ ⋅−+=
..
,
SC
SCCCVCV sdVRRVmP

ρor
The Linear Momentum, of the differential mass dm = ρdv is defined as
vdVmdVPd II
ρ,,
:

==
FLUID DYNAMICS

28. 28
BASIC LAWS IN FLUID DYNAMICS
(2) CONSERVATION OF LINEAR MOMENTUM (C.L.M.) (CONTINUE - 1)
SOLO
Using Newton’s Second Law, for the
mass element dm = ρdv, we obtain:
ext
fd

- Differential external forces acting on dm
ij
fd int

- Differential internal forces acting on dm
I
I
td
Rd
VV


== ,
: - Velocity of the mass element dm relative to I.
- mass flow rate entering the system through the element of C.S.mdsdVS


=⋅− ,ρ sd

vd
tD
VD
md
tD
VD
fdfd
II
ext
ρ==+ int

VV
t
V
tD
VD
I
II


,
∇⋅+
∂
∂
= - Material derivative of the Velocity of the mass element dm relative to I.V

- Velocity of mass exiting the system, relative to the element of C.S.SV,

sd

FLUID DYNAMICS

29. 29
BASIC LAWS IN FLUID DYNAMICS
(2) CONSERVATION OF LINEAR MOMENTUM (C.L.M.) (CONTINUE - 2)
SOLO
Let integrate the equation
vd
tD
VD
md
tD
VD
fdfd
II
ext
ρ==+ int

over the mass enclosed by C.V.
From the 3rd
Newton’s Law the internal forces that particle j applies on particle i is of
equal magnitude but of opposite direction to the force that particle i applies on
particle j, therefore :
∫∫∫∫∫∫∫∫∫ =+
..
0
..
int
.. VC
I
VCVC
ext vd
tD
VD
fdfd ρ


Using Reynolds’ Transport Theorem we obtain
( ) ( )∫∫∫∫∫∫∫∫∫∫∫∫∫∑ ⋅+=⋅+===
..
,
..
,
......
,
SC
S
I
CV
SC
S
I
VC
REYNOLDS
VC
I
VC
extCVext sdVV
td
Pd
sdVVvdV
td
d
vd
tD
VD
fdF



ρρρρ
FLUID DYNAMICS

30. 30
( ) ( ) ( ) ∑∑∫∫∫∫∫∫∫∫∫∫∫∫∫∫∫ =++−+=⋅+=⋅+=
=⋅−−
ext
j
j
SC
sdTsd
VCSC
md
S
I
CV
SC
md
S
I
VC
REYNOLDS
VC
I
FFdstfnpvdgsdVV
td
Pd
sdVVvdV
td
d
vd
tD
VD 
  








......
,
..
,
....
11
σ
ρρρρρ
BASIC LAWS IN FLUID DYNAMICS
(2)CONSERVATION OF LINEAR MOMENTUM (C.L.M.) (CONTINUE - 3)
SOLO
The external forces acting on the system are:
• Gravitation acceleration (E center of Earth).E
E
R
R
M
Gg

3
=
( ) dstfnpsdTsdnsd

111 +−==⋅=⋅ σσ
where:
( ) ndsnnsdsd

111 =⋅= - vector of surface differential
( )2
/mNp - pressure on (normal to) the surface .
( ) ∑∫∫∫∫∫∫∫∫∑ ++−+==
=⋅
j
j
SC
sdTsd
VCVC
extext FdstfnpvdgfdF

  

......
11
σ
ρ
f - friction force per (parallel to) unit surface .( )2
/mN
• Discrete force exerting by the surrounding on the point , and discrete moments .∑j
jF

jR

∑
k
kM

nT

1⋅= σ - force per unit surface ( )2
/mN
Therefore:
• Surface forces acting on the system:
FLUID DYNAMICS

31. 31
FLUID DYNAMICS
BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.2) CONSERVATION OF LINEAR MOMENTUM (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
C.L.M.-2
Since this is true for all volumes vF(t) attached to the fluid we can drop the volume integral.
[ ] [ ] [ ]τσ
τρσρ
∂
∂
ρ
∂
∂
ρρ
~~
~~
2
1
,,,
,
2
,
,
.).(
+−=
⋅∇+∇−=⋅∇+=








×∇×−





∇+=








∇⋅+=
Ip
pGG
uuu
t
u
uu
t
u
tD
uD
III
II
I
I
I
DM
I





ikikik
i
ik
i
i
i
ik
i
k
i
k
i
j
jjj
i
i
k
i
k
i
DM
i
p
xx
p
G
x
G
x
u
u
x
u
uuu
xt
u
x
u
u
t
u
tD
uD
τδσ
∂
τ∂
∂
∂
ρ
∂
σ∂
ρ
∂
∂
∂
∂
∂
∂
∂
∂
ρ
∂
∂
∂
∂
ρρ
+−=
+−=+=












⋅−⋅−





+=






⋅+=
2
1
.).(
SOLO
Derivation From Integral Form (Continue)
( )∫∫∫
∫∫∫∫∫∫∫∫
⋅∇+=
⋅+=
)(
,
)()()(
,
~
~
tv
I
tStvtv
I
I
F
FFF
vdG
sdvdGvd
tD
uD
σρ
σρρ


∫∫∫
∫∫∫∫∫∫∫∫






+=
+=
)(
)()()(
tv i
ik
i
tS
kik
tv
i
tv
i
F
FFF
vd
x
G
sdvdGvd
tD
uD
∂
σ∂
ρ
σρρ

32. 32
BASIC LAWS IN FLUID DYNAMICS
(2)CONSERVATION OF LINEAR MOMENTUM (C.L.M.)
SOLO
Let compute the C.L.M. in the tangential to the
wheel direction, for the Pelton Water Wheel
( )[ ]
( ) ( )
t
tvtv
extjj RfdfdrVrQVQ −+=−−− ∫∫





0
int
0
cos βωωρρ
where
( ) ( )∫∫∫∫ ⋅−=⋅−=
outin A
S
A
S
sdVsdVQ

,,
: ρρρ
( ) ( )βωρ cos1+−= rVQR jt
Therefore
The average Torque on the water wheel is ( ) ( )βωρ cos1+−== rVrQrRTorque jt
The Power developed is ( ) ( )βωωρω cos1+−==⋅= rVrQrRTorquePower jt
The average Tangential Reaction Force on
the bucket is
In steady-state the directions and
magnitudes of flows are fixed, therefore
0
..


== ∫∫∫
I
VC
I
CV
vdV
td
d
td
Pd
ρ
( ) ( )
∑∑∫∫∫∫∫
∫∫∫∫∫∫∫
=+⋅+=
⋅+=⋅+
−−
ext
j
j
SCVC
SC
md
S
I
CV
SC
md
S
I
VC
FFsdvdg
sdVV
td
Pd
sdVVvdV
td
d







....
..
,
..
,
..
σρ
ρρρ
Example
FLUID DYNAMICS

33. 33
Ramjet
SOLO
(2) CONSERVATION OF LINEAR MOMENTUM (C.L.M.)
( ) ( ) ∫∫∫∫ ⋅⋅−⋅++−+=
→→
WW AA
x sdxsdxpApumApumF

 τ~1100006666
( ) ( ) ∫∫∫∫ −++−+=
WW A
WA
A
WA AdAdpApuApu θτθρρ sinsin00
2
0066
2
66
( ) 6060
2
006
2
66 AppAuAu −+−= ρρ 60 Ap−←
( )∫∫ −−
WA
WA Adpp θsin0
∫∫+←
WA
WAdp θsin0
  
0
600 sin








−+− ∫∫ AAAdp
WA
Wθ
600 sin ApAdp
WA
W +−← ∫∫ θ
∫∫−
WA
WA Adθτ sin
1 2 30 4 5 6
SUPERSONIC
COMPRESSION
SUBSONIC
COMPRESSION
COMBUSTION
FUEL
INJECTION EXPANSION
NOZZLECOMBUSTION
CHAMBER
DIFFUSER
FLAME
HOLDERS
EXHAUST
JET
0V
0A
fm
x
BASIC LAWS IN FLUID DYNAMICS
FLUID DYNAMICS

34. 34
Ramjet
SOLO
CONSERVATION OF LINEAR MOMENTUM (C.L.M.) (continue – 1)
( ) ( )
    
  
DRAGFRICTION
A
WA
DRAGPRESURE
A
WA
THRUST
x
WW
AdAdppAppAuAuF ∫∫∫∫ −−−−+−= θτθρρ sinsin06060
2
006
2
66
00000666 & mAummAu f
 =+= ρρUsing C.M.
( ) ( ) 0006060
2
006
2
66 umummAppAuAuTHRUST ef
 −+=−+−= ρρ
or
we obtain
( )[ ] ( ) 060600 /:1 mmfAppuufmTHRUST fe
 =−+−+==T
and ( )
    
DRAGFRICTION
A
WA
DRAGPRESURE
A
WA
WW
AdAdppDRAGD ∫∫∫∫ +−== θτθ sinsin0
1 2 30 4 5 6
SUPERSONIC
COMPRESSION
SUBSONIC
COMPRESSION
COMBUSTION
FUEL
INJECTION EXPANSION
NOZZLECOMBUSTION
CHAMBER
DIFFUSER
FLAME
HOLDERS
EXHAUST
JET
0V
0A
fm
x
BASIC LAWS IN FLUID DYNAMICS
FLUID DYNAMICS
Return to Table of Content

35. 35
( ) ( ) PdRRvdVRRHd OOO

×−=×−= ρ,
BASIC LAWS IN FLUID DYNAMICS
(3)CONSERVATION OF MOMENT-OF-MOMENTUM (C.M.M.)
SOLO
The Absolute Angular Momentum, of the differential mass
and Inertial Velocity ,relative to a reference point O is defined as
vdmd ρ=
V

The Absolute Angular Momentum of the mass
enclosed by C.V. is defined as
( ) ( )∫∫∫∫∫∫ ×−=×−=
....
,
VC
O
VC
OOCV
PdRRvdVRRH

ρ
Let differentiate the Absolute Angular Momentum
and use Reynolds’ Transport Theorem
( ) ( ) ( ) ( )∫∫∫∫∫∫∫∫ ⋅−×−+
×−
=×−=
..
,
....
,
SC
md
SO
VC
I
O
REYNOLDS
I
VC
O
I
OCV
sdVVRRvd
tD
VRRD
vdVRR
td
d
td
Hd






ρρρ
We have ( ) ( )
( ) ( ) ( ) VV
tD
VD
RRVVV
tD
VD
RR
V
tD
RD
tD
RD
tD
VD
RR
tD
VRRD
O
I
OO
I
O
I
O
II
O
I
O









×−×−=×−+×−=
×








−+×−=
×−
FLUID DYNAMICS

36. 36
( ) ( ) ( ) int,
: fdRRfdRRvd
tD
VD
RRMd OextO
I
OO



×−+×−=×−= ρ
( ) ( ) ( ) ( )∫∫∫∫∫∫∫∫∫∫∫ ⋅−×−+×−×−=×−=
..
,
......
,
SC
md
SO
P
VC
O
VC
I
O
REYNOLDS
I
VC
O
I
OCV
sdVVRRvdVVvd
tD
VD
RRvdVRR
td
d
td
Hd
CV








ρρρρ
BASIC LAWS IN FLUID DYNAMICS
(3) CONSERVATION OF MOMENT-OF-MOMENTUM (C.M.M.)
SOLO
The Moment, of the differential mass dm = ρdv, relative to a reference
point O is defined as
Therefore
Let integrate this equation over the control volume C.V.
( ) ( ) ( )
  




0
..
int
....
, ∫∫∫∫∫∫∫∫∫∑ ×−+×−=×−=
VC
O
VC
extO
VC I
OOCV fdRRfdRRvd
tD
VD
RRM ρ
Using the differential of Angular Momentum equation we obtain
( ) ( ) ( )∫∫∫∫∫∑∫∫∫ ⋅−×−+×−=×−=
..
,
..
,
..
,
SC
md
SO
P
VC
OOCV
I
VC
O
I
OCV
sdVVRRvdVVMvdVRR
td
d
td
Hd
CV






ρρρ
( ) ( ) ( ) ( ) ( ) ∑∑∫∫∫∫∫∫∫∫∑ +×−++−×−+×−=×−=
=⋅
k
k
j
jOj
SC sdTsd
O
VC
O
VC
extOOtCV MFRRsdtfnpRRvdgRRfdRRM

  

......
, 11
σ
ρ
Also
( )∑ ×−
j
jOj FRR

- Moment, relative to O, of discrete forces exerting by the surrounding at point jR

- Discrete Moments exerting by the surrounding.∑
k
k
M

FLUID DYNAMICS

37. 37
( ) ( ) ( ) ∑∑∫∫∫∫∫∫∫∫∫∫∫∫∫∫∑ +×++−×+×=×+⋅−×−×=×−=
=⋅
k
k
j
jO
SC
sdTsd
O
VC
O
P
VC
O
SC
md
SO
IVC
O
VC Ir
OOCV MFrsdtfnprvdgrvdVVsdVVrvdVr
td
d
vd
tD
VD
RRM
CV
O

  












,
..
,
..
,
....
,,
..
,
Reynolds
..
, 11
, σ
ρρρρρ
BASIC LAWS IN FLUID DYNAMICS
(3)CONSERVATION OF MOMENT-OF-MOMENTUM (C.M.M.)
SOLO
Let find the equation of moment around the
turbomachine axis.
We shall use polar coordinates , where z is
the turbomachine axis.
zr ,,θ
zzrrrO
ˆˆ, +=

zVVrVV zr
ˆˆˆ ++= θθ

zFFrFF zr
ˆˆˆ ++= θθ

( ) zVrVrVzrVz
VVV
zr
zr
Vr zrz
zr
O
ˆˆ0
ˆˆˆ
, θ
θ
θ
+−+−==×

( )  ( )
∑∑∫∫∫∫ ++=×+⋅−−
k
kz
j
j
tv
extCVO
SC
S
VC
MFrdfrPVsdVVrvdVr
td
d
θθθθ ρρ


0
..
,
..
The moment of momentum equation around the turbomachine z axis.
Example
FLUID DYNAMICS

38. 38
BASIC LAWS IN FLUID DYNAMICS
(3) CONSERVATION OF MOMENT-OF-MOMENTUM (C.M.M.)
SOLO
( )
( ) ( ) ( ) ( )
( )
    

  
systemoutsidefromexertedTorque
M
l
lz
j
j
tv
ext
AVVrAVVr
SC
S
statesteady
VC
zSnSn
MFrdfrsdVVrvdVr
td
d
∑∑∫∫∫∫ ++=⋅−−
+−−→
θθ
ρρ
θθ
θθ
ρρ
22,21111,122
..
,
0
..
We obtain
( ) ( )[ ] zflow
MQVrVr =− 111122
ρθθ
or
( ) ( ) ( ) ( ) ( ) ( )[ ] ( ) zSnSnSn
MAVVrVrAVVrAVVr =−=− 11,1112211,11122,222
ρρρ θθθθ
Euler Turbine Equation
ρ1 - mean fluid density one inlet (1) of area A1.
where
ρ2 - mean fluid density one outlet (2) of area A2.
(Vθ )1, r1 - mean fluid tangential velocity and radius one inlet (1) of area A1.
(Vθ )2, r2 - mean fluid tangential velocity and radius one outlet (2) of area A2.
(V,Sn )1 - mean fluid normal velocity (relative to A1) one inlet (1) of area A1.
(V,Sn )2 - mean fluid normal velocity (relative to A2) one outlet (2) of area A2.
- mean flow rate one outlet (1) of area A1.( ) 11,1 : AVQ Snflow =
Leonhard Euler
(1707-1783)
FLUID DYNAMICS
Return to Table of Content

39. 39
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.4) CONSERVATION OF ENERGY (C.E.)
– THE FIRST LAW OF THERMODYNAMICS (DIFFERENTIAL FORM)
- Fluid mean velocity( ) 
u r t, ( )sec/m
- Body Forces Acceleration
- (gravitation, electromagnetic,..)
G

- Surface Stress ( )2
/ mNT

nnpnT ˆ~ˆˆ~ ⋅+−=⋅= τσ

m
V(t)
G
q
T n= ⋅~σ
d E
d t
∂
∂
Q
t
uu
d s n ds=
- Internal Energy of Fluid molecules
(vibration, rotation, translation)
per volume
e
3
/ mJ
- Rate of Heat transferred to the Control Volume
(chemical, external sources of heat) ( )3
/ mW
∂
∂
Q
t
- Rate of Work change done on fluid by the surrounding (rotating shaft, others)
(positive for a compressor, negative for a turbine)td
Ed
( )3
/ mW
SOLO
Consider a volume vF(t) attached to the fluid, bounded by the closed surface SF(t).
- Rate of Conduction and Radiation of Heat from the Control Surface
(per unit surface)
q
( )2
/ mW

40. 40
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.4) CONSERVATION OF ENERGY (C.E.)
– THE FIRST LAW OF THERMODYNAMICS (CONTINUE - 1)
- The Internal Energy of the molecules of the fluid plus the
Kinetic Energy of the mass moving relative to an
Inertial System (I)
The FIRST LAW OF THERMODYNAMICS
CHANGE OF INTERNAL ENERGY + KINETIC ENERGY =
CHANGE DUE TO HEAT + WORK + ENERGY SUPPLIED BY SUROUNDING
SOLO
The energy of the constant mass m in the volume vF(t) attached to the fluid,
bounded by the closed surface SF(t) is
This energy will change due to
- The Work done by the surrounding
- Absorption of Heat
- Other forms of energy supplied to the mass
(electromagnetic, chemical,…)

41. 41
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.4) CONSERVATION OF ENERGY (C.E.)
– THE FIRST LAW OF THERMODYNAMICS (CONTINUE - 2)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
C.E.-1
  

  




  
systementering
td
Qd
tSv
systemontnmenenvirobydone
td
Wd
shaft
tSv
v
REYNOLDS
KineticInternal
tv
FF
FF
FF
sdqvd
t
Q
td
Wd
ForcesSurface
sdTu
ForcesBody
vdGu
vdue
tD
D
vdue
td
d
∫∫∫∫∫
∫∫∫∫∫
∫∫∫∫∫∫
⋅−+
+⋅+⋅=






+=





+
+
)(
)(
2
)3(
)(
2
2
1
2
1
∂
∂
ρ
ρρ
  
  
  
  
systementering
td
Qd
tS
kk
tv
systemontnemnoenvirbydone
td
Wd
shaft
tS
kk
tv
kk
tv
REYNOLDS
KineticInternal
tv
FF
FF
FF
dsqvd
t
Q
td
Wd
ForcesSurface
sdTu
ForcesBody
vdGu
vdue
tD
D
vdue
td
d
∫∫∫∫∫
∫∫∫∫∫
∫∫∫∫∫∫
−+
++=






+=





+
+
)()(
)()(
)(
2
)3(
)(
2
2
1
2
1
∂
∂
ρ
ρρ
SOLO

42. 42
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.4) CONSERVATION OF ENERGY (C.E.)
– THE FIRST LAW OF THERMODYNAMICS (CONTINUE - 3)
VECTOR NOTATION CARTESIAN TENSOR NOTATIONC.E.-2
( ) ( )
∫∫∫∫∫∫
∫∫∫∫∫∫∫∫∫
∫∫∫∫∫
∫∫∫∫∫∫∫
∫∫∫
⋅∇−+
⋅⋅∇+⋅∇−⋅=
⋅−+
⋅⋅+⋅−⋅=
+






+
)()(
)()()(
)1(
)()(
)()()(
)(
2
~
~
2
1
tvtv
tvtvtv
GAUSS
td
Qd
tStv
td
Wd
tStStv
tv
FF
FFF
FF
FFF
F
vdqvd
t
Q
vduvdupvdGu
sdqvd
t
Q
sdusdupvdGu
KineticInternal
vdue
tD
D


  

  

  
∂
∂
τρ
∂
∂
τρ
ρ
( ) ( )
∫∫∫∫∫∫
∫∫∫∫∫∫∫∫∫=
∫∫∫∫∫
∫∫∫∫∫∫∫
∫∫∫
−+
+−
−+
+−=






+
+
)()(
)()()(
)1(
)()(
)()()(
)(
2
2
1
tV s
s
tV
tV
k
k
iki
tV
k
k
k
tV
kk
GAUSS
td
Qd
tS
kk
tV
td
Wd
tS
kiki
tS
kk
tV
kk
KineticInternal
tV
vd
x
q
vd
t
Q
ds
x
u
ds
x
up
vdGu
dsqvd
t
Q
dsudsupvdGu
vdue
tD
D
∂
∂
∂
∂
∂
τ∂
∂
∂
ρ
∂
∂
τρ
ρ
  
  
  
     
T n pn n ds n ds= ⋅ = − + ⋅ =~ ~ &σ τ0=
td
Wd shaft
assume and use
SOLO

43. 43
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.4) CONSERVATION OF ENERGY (C.E.)
– THE FIRST LAW OF THERMODYNAMICS (CONTINUE-4)
VECTOR NOTATION CARTESIAN TENSOR NOTATIONC.E.-3
Since the last equation is valid for each vF(t) we can drop the integral and obtain:
( ) ( )
q
t
Q
uGuupue
tD
D


⋅∇−+
⋅+⋅⋅∇+⋅−∇=





+
∂
∂
ρτρ ~
2
1 2 ( ) ( )
k
k
kk
k
iik
k
k
x
q
t
Q
uG
x
u
x
up
ue
tD
D
∂
∂
∂
∂
ρ
∂
τ∂
∂
∂
ρ
−+
++−=





+ 2
2
1
Multiply (C.L.M.-2) by

u
τρρ ~⋅∇⋅+∇⋅−⋅=⋅ upuuG
tD
uD
u


( )
k
ik
i
k
kkk
i
i
x
u
x
p
uuGu
tD
D
tD
uD
u
∂
τ∂
∂
∂
ρρρ +−== 2
Subtract this equation from (C.E.-3)
C.E.-4
( )[ ]ρ τ τ
∂
∂
D e
D t
p u u u
Q
t
q
= − ∇⋅ + ∇⋅ ⋅ − ⋅∇⋅
+ −∇⋅
  
  

~ ~
Φ
ρ
∂
∂
τ
∂
∂
∂
∂
∂
∂
D e
D t
p
u
x
u
u
x
Q
t
q
x
k
k
ik
i
k
k
k
=− +
+ −
Φ
 
( )Φ ≡ ∇⋅ ⋅ − ⋅∇ ⋅ >~ ~τ τ
 
u u 0
Φ ≡ >τ
∂
∂
ik
i
k
u
x
0
(Proof of inequality given later)
SOLO

44. 44
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.4) CONSERVATION OF ENERGY (C.E.)
– THE FIRST LAW OF THERMODYNAMICS (CONTINUE - 5)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
Enthalpy
Use this result and (C.E.-4)
C.E.-5
ρ
p
eh +=:
( )
tD
pD
up
tD
hD
u
p
tD
pD
tD
hD
tD
Dp
tD
pD
tD
hD
tD
pD
tD
hD
tD
eD
−⋅∇−=⋅∇−+−=
+−=






−=

ρρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρρρ 2
tD
pD
x
u
p
tD
hD
x
up
tD
pD
tD
hD
tD
pDp
tD
hD
tD
pD
tD
pD
tD
hD
tD
eD
k
k
k
k
−−=







−+−=
+−=






−=
∂
∂
ρ
∂
∂
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρρρ 2
Φ++⋅∇−=
t
Q
q
tD
pD
tD
hD
∂
∂
ρ

Φ++−=
t
Q
x
q
tD
pD
tD
hD
k
k
∂
∂
∂
∂
ρ
SOLO
( )Φ ≡ ∇⋅ ⋅ − ⋅∇ ⋅ >~ ~τ τ
 
u u 0
Φ ≡ >τ
∂
∂
ik
i
k
u
x
0

45. 45
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.4) CONSERVATION OF ENERGY (C.E.)
– THE FIRST LAW OF THERMODYNAMICS (CONTINUE - 6)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
Total Enthalpy
Use this result and (C.E.-3)
C.E.-6
22
2
1
2
1
: u
p
euhH ++=+=
ρ
( )
t
p
up
tD
HD
tD
pD
up
tD
HD
p
tD
D
tD
HD
ue
tD
D
∂
∂
ρρ
ρ
ρρρ
−⋅∇−=−⋅∇−=






−=





+

2
2
1
( )
t
p
up
xtD
HD
tD
pD
x
u
p
tD
HD
p
tD
D
tD
HD
ue
tD
D
kk
k
∂
∂
∂
∂
ρ
∂
∂
ρ
ρ
ρρρ
−−=−−=






−=





+

2
2
1
( ) q
t
Q
uGu
t
p
tD
HD 
⋅∇−+⋅+⋅⋅∇+=
∂
∂
ρτ
∂
∂
ρ ~ ( )
k
k
kk
k
iik
x
q
t
Q
uG
x
u
t
p
tD
HD
∂
∂
∂
∂
ρ
∂
τ∂
∂
∂
ρ −+++=
SOLO

46. 46
BASIC LAWS IN FLUID DYNAMICS
(4) THE FIRST LAW OF THERMODYNAMICS
SOLO
Let apply the First Law of Thermodynamics
to an element of fluid of mass dmfluid
  
fluidfluidfluid dmondone
WorkExternal
dmto
addedHeat
dmof
ChangeEnergyTotal
WQEd δδ +=













++





=

 EnergyPotential
fluid
EnergyInternal
fluid
EnergyKinetic
fluid
dmof
ChngeEnergyTotal
mdhgmdumd
V
dEd
fluid
2
2

      
boundaryliquidatDone
mdinside
volumeandpressure
changetodoneWork
fluidfluidfluid
Frictionby
LosesSystem
fluid
fluid
Losses
LiquidShaft
boundaryatDone
fluid
fluid
shaft
dmondone
WorkExternal
fluid
fluid
md
pd
md
p
md
pmd
md
Wd
dmd
md
Wd
dW






















+−+














−














=
−
ρρρ
δ
We obtain






−








−








+=++





ρ
δ p
d
md
Wd
d
md
Wd
d
md
Q
zdgud
V
d
fluid
loss
fluid
shaft
fluid2
2
First Law of Thermodynamics
FLUID DYNAMICS
Return to Table of Content

47. 47
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
SOLO
THERMODYNAMIC PROCESSES
1. ADIABATIC PROCESSES
2. REVERSIBLE PROCESSES
3. ISENTROPIC PROCESSES
No Heat is added or taken away from the System
No dissipative phenomena (viscosity, thermal, conductivity, mass diffusion,
friction, etc)
Both adiabatic and reversible
(2.5) THE SECOND LAW OF THERMODYNAMICS AND ENTROPY PRODUCTION

48. 48
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.5) THE SECOND LAW OF THERMODYNAMICS AND ENTROPY PRODUCTION
2nd
LAW OF THERMODYNAMICS
Using GAUSS’ THEOREM
0
)()(
≥+ ∫∫∫∫∫
tStv FF
Ad
T
q
vds
td
d

ρ
00
)(
)1(
)()(
≥











⋅∇+⇒≥+ ∫∫∫∫∫∫∫∫
tv
GAUSS
tStv FFF
vd
T
q
tD
sD
Ad
T
q
vd
tD
sD

ρρ
- Change in Entropy per unit volumed s
- Local TemperatureT [ ]K
- Fluid Densityρ [ ]3
/ mKg
d e q w T ds pdv= + = −δ δ d s
d e
T
p
T
dv= +
SOLO
For a Reversible Process
- Rate of Conduction and Radiation of Heat from the System
per unit surface
q

[ ]2
/ mW
Gibbs Relation
Josiah Willard Gibbs
(1839-1903)

49. 49
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.5) THE SECOND LAW OF THERMODYNAMICS (CONTINUE - 1)
d e q w T ds pdv= + = −δ δ d s
d e
T
p
T
dv= +
u
T
p
tD
eD
T
u
T
p
tD
eD
T
tD
D
T
p
tD
eD
TtD
D
T
p
tD
eD
TtD
vD
T
p
tD
eD
TtD
sD
u
tD
D
MC
v


⋅∇+=





⋅∇+=






−+=





+=+=
⋅∇−=
=
ρ
ρ
ρ
ρρ
ρ
ρ
ρρ
ρ
ρρρρ
ρ
ρ
ρ
ρ
2
.).(
2
1
1
11
The Energy Equation (C.E.-4) is
( )
k
i
ik
x
u
oruu
t
Q
qup
tD
eD
∂
∂
τττ
∂
∂
ρ =Φ⋅∇⋅−⋅⋅∇=ΦΦ++⋅∇−⋅∇−= ~~ 
Tt
Q
TT
q
up
tD
eD
TtD
sD Φ
++
⋅∇
−=





⋅∇+=
∂
∂
ρ
11


or
Φ++⋅−∇=
t
Q
q
tD
sD
T
∂
∂
ρ

SOLO

50. 50
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.5) THE SECOND LAW OF THERMODYNAMICS (CONTINUE - 2)
Define
ρ
∂
∂
T
D s
Dt
q
Q
t
= −∇ ⋅ + +

Φ
Θ ≡ + ∇ ⋅





 ≥ρ
Ds
Dt
q
T

0 Entropy Production Rate per unit volume
Therefore
( )
Θ
Φ
Θ= −
∇ ⋅
+ + + ∇ ⋅





 ≥∫∫∫
 
q
T T
Q
t T
q
T
dv
V t
1
0
∂
∂
&
SOLO

51. 51
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.5) THE SECOND LAW OF THERMODYNAMICS (CONTINUE - 3)
  

q q q
q conduction rate per unit surface
q radiation rate per unit surfacec r
c
r
= +




q K T K FOURIER s Conduction Lawc = − ∇ > 0 '
( )−
∇ ⋅
+ ∇ ⋅





 = −
∇ ⋅
+ ∇ ⋅ + ⋅∇





 = ⋅∇





 = − ∇ + ⋅∇






= − ∇ ⋅ − ∇





 + ⋅∇





 =
∇




 + ⋅∇






  
   
 
q
T
q
T
q
T T
q q
T
q
T
K T q
T
K T
T
T q
T
K
T
T
q
T
r
r r
1 1 1 1
1 1 1
2
2
Θ
Φ
Φ=
∇




 + + + ⋅∇






>
>
>





K
T
T T T
Q
t
q
T
K
T
r
2
1 1
0
0
0
∂
∂

Θ
Φ
≡ + ∇⋅





 =
∇




 + + + ⋅∇





 ≥ρ
∂
∂
D s
D t
q
T
K
T
T T T
Q
t
q
Tr


2
1 1
0
SOLO
JEAN FOURIER
1768-1830

52. 52
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.5) THE SECOND LAW OF THERMODYNAMICS (CONTINUE - 4)
SOLO
Gibbs Function
Helmholtz Function
sThG ⋅−=:
sTeH ⋅−=:
Josiah Willard Gibbs
(1839-1903)
Hermann Ludwig Ferdinand
von Helmholtz
(1821 – 1894)
Using the Relations
vdpsdTed ⋅−⋅=
( ) pdvsdTvpdedhd ⋅+⋅=⋅+=vpe
p
eh ⋅+=+=
ρ
:
pdvTdssdTTdshdGd ⋅+⋅−=⋅−⋅−=
vdpTdsTdssdTedHd ⋅−⋅−=⋅−⋅−=
dv
T
p
T
ed
sd +=

53. 53
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.5) THE SECOND LAW OF THERMODYNAMICS (CONTINUE - 5)
SOLO
Maxwell’s Relations
vdpsdTed ⋅−⋅=
pdvsdThd ⋅+⋅=
pdvTdsGd ⋅+⋅−=
vdpTdsHd ⋅−⋅−=
Ts
pv
v
F
p
v
e
s
h
T
s
e






∂
∂
=−=





∂
∂






∂
∂
==





∂
∂
vp
Ts
T
F
s
T
G
p
G
v
p
h






∂
∂
=−=





∂
∂






∂
∂
==





∂
∂
ps
vs
s
v
p
T
s
p
v
T






∂
∂
=





∂
∂






∂
∂
−=





∂
∂
vT
pT
T
p
v
s
T
v
p
s






∂
∂
=





∂
∂






∂
∂
−=





∂
∂
James Clerk Maxwell
(1831-1879)
Return to Table of Content

54. 54
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6) CONSTITUTIVE RELATIONS FOR GASES
(2.6.1) NEWTONIAN FLUID DEFINITION – NAVIER–STOKES EQUATIONS
[ ] τσ ~~ +−= Ip
Stress
NEWTONIAN FLUID:
The Shear Stress on
A Surface Parallel
to the Flow =
Distance Rate of
Change of Velocity
SOLO
CARTESIAN TENSOR NOTATION
ikikik p τδσ +−=
VECTOR NOTATION
- Stress tensor (force per unit surface) of the surrounding
on the control surface ( )2
/ mN
σ~
- Shear stress tensor (force per unit surface) of the surrounding on the control
surface ( )2
/ mN
τ~

55. 55
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6) CONSTITUTIVE RELATIONS
(2.6.1) NEWTONIAN FLUID DEFINITION – NAVIER–STOKES EQUATIONS
M. NAVIER 1822
INCOMPRESSIBLE FLUIDS
(MOLECULAR MODEL)
G.G. STOKES 1845
COMPRESSIBLE FLUIDS
(MACROSCOPIC MODEL)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
[ ] [ ] ( )[ ] [ ]IuuuIpIp
T 
∇+∇+∇+−=+−= λµτσ ~~
ik
k
k
i
k
k
i
ikikikik
x
u
x
u
x
u
pp δ
∂
∂
λ
∂
∂
∂
∂
µδτδσ +





++−=+−=
( )[ ] [ ]( ) ( ) ( ) µλλµλµτ
3
2
32~0 −=⇒∇+∇=∇+∇+∇== utrutrIutruutrtr
T 
( ) µλ
∂
∂
λµδ
∂
∂
λ
∂
∂
µτ
3
2
0322 −=⇒=+=+=
i
i
ik
k
k
i
i
ii
x
u
x
u
x
u
SOLO
STOKES ASSUMPTION µλ
3
2
−=0~ =τtrace
μ, λ - Lamé parameters from Elasticity

56. 56
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6) CONSTITUTIVE RELATIONS
(2.6.1) NAVIER–STOKES EQUATIONS (CONTINUE)
(2.6.1.2) VECTORIAL DERIVATION
I
x
y
z
T n= ⋅~σ
d s n ds=
r
dru
u +du( )unrdtd
t
u
urdtd
t
u
ud





∇⋅+=∇⋅+= 1
∂
∂
∂
∂
( ) ( ) ( ) rdnurdnuuntd
t
u
ud
RotationnTranslatio


  



1
2
1
1
2
1
1 ××∇+





××∇−∇⋅+=
∂
∂
OR
DEFINITION OF NEWTONIAN FLUID, NAVIER-STOKES EQUATION
( ) ( ) nnunuunnpT
nTranslatio

  

1~11
2
1
121 ⋅=⋅∇+





××∇−∇⋅+−≡ σλµ
CONSERVATION OF LINEAR MOMENTUM EQUATIONS
SOLO

57. 57
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6) CONSTITUTIVE RELATIONS
(2.6.1) NAVIER–STOKES EQUATIONS (CONTINUE)
(2.6.1.2)VECTORIAL DERIVATION (CONTINUE) I
x
y
z
T n= ⋅~σ
d s n ds=
r
dru
u + du
CONSERVATION OF LINEAR MOMENTUM
EQUATIONS
( ) ( )
( ) ( ) ( )
( )
 ( )
( )
( )
( )
( )
( )
∫∫∫
∫∫∫∫∫∫∫∫∫∫∫
∫∫∫∫∫∫∫∫∫∫∫∫∫∫∫










⋅∇∇+×∇×∇+∇⋅∇+∇−=
=⋅∇+×∇×+∇⋅+−=






⋅∇+





××∇−∇⋅+⋅−=+=
)(
)()()()()(
)()()()()()(
251
2
2
2
11
2
1
121
tV
GAUSS
tStStStStV
tStStVtStVtV
vd
GAUSS
u
GAUSS
u
GAUSS
u
GAUSS
pG
usdusdusdsdpvdG
sdnunuunsdnpvdGdsTvdGvd
tD
uD








λµµρ
λµµρ
λµρρρ
BUT
( ) ( ) ( )∇× ∇× ≡ ∇ ∇⋅ − ∇⋅ ∇2 2 2µ µ µ
  
u u u
( ) ( ) ( ) ( )∇⋅ ∇ + ∇× ∇× = ∇ ∇⋅ − ∇× ∇×2 2µ µ µ µ
   
u u u u
THEN
SOLO

58. 58
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
I
x
y
z
T n= ⋅~σ
d s n ds=
r
dru
u + du
THEREFORE
( ) ( ) ( ){ }∫∫∫∫∫∫ ⋅∇∇+×∇×∇−⋅∇∇+∇−=
)()(
2
tVtV
vduuupGvd
tD
uD 
λµµρρ
OR
( ) ( )[ ]uupG
tD
uD 
⋅∇+∇+×∇×∇−∇−= µλµρρ 2
SOLO
(2.6) CONSTITUTIVE RELATIONS
(2.6.1) NAVIER–STOKES EQUATIONS (CONTINUE)
(2.6.1.2)VECTORIAL DERIVATION (CONTINUE)

59. 59
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
CONSERVATION OF LINEAR MOMENTUM
( ) ( )[ ]∇ ⋅ = − ∇ − ∇ × ∇ × + ∇ + ∇ ⋅~σ µ µ λp u u
 
2 ( ) 





++











++−=
k
k
ii
k
k
i
iii
ik
x
u
xx
u
x
u
xx
p
x ∂
∂
λµ
∂
∂
∂
∂
∂
∂
µ
∂
∂
∂
∂
∂
σ∂
2
( ) ( )[ ]
ρ ρ σ
ρ µ µ λ
Du
Dt
G
G p u u
 
  
= + ∇ ⋅
= − ∇ − ∇ × ∇ × + ∇ + ∇ ⋅
~
2 ( ) 





++











++−=
+=
k
k
ii
k
k
i
ii
i
i
ik
i
i
x
u
xx
u
x
u
xx
p
G
x
G
tD
uD
∂
∂
λµ
∂
∂
∂
∂
∂
∂
µ
∂
∂
∂
∂
ρ
∂
σ∂
ρρ
2
USING STOKES ASSUMPTION tr ~τ λ µ= ⇒ = −0
2
3
( ) 



⋅∇∇+×∇×∇−∇−=
⋅∇+=
uupG
G
tD
uD


µµρ
σρρ
3
4
~






+











++−=
+=
k
k
ki
k
k
i
kk
i
k
ik
i
i
x
u
xx
u
x
u
xx
p
G
x
G
tD
uD
∂
∂
µ
∂
∂
∂
∂
∂
∂
µ
∂
∂
∂
∂
ρ
∂
σ∂
ρρ
3
4
SOLO
(2.6) CONSTITUTIVE RELATIONS
(2.6.1) NAVIER–STOKES EQUATIONS (CONTINUE)

60. 60
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
VECTOR NOTATION CARTESIAN TENSOR NOTATION
Euler Equations are obtained by assuming Inviscid Flow
0
3
2
0~ =−=⇒= µλτ
pG
tD
uD
∇−=

ρρ
i
i
i
x
p
G
tD
uD
∂
∂
ρρ −=
SOLO
(2.6) CONSTITUTIVE RELATIONS
(2.6.2) EULER EQUATIONS
pGuu
t
u
∇−=





∇⋅+
∂
∂ 

ρρ
i
i
k
i
k
i
x
p
G
x
u
u
t
u
∂
∂
ρρ −=





∂
∂
+
∂
∂
or or
Leonhard Euler
(1707-1783)

61. 61
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6.1.3) COMPUTATION
BUT
Φ
Φ = = +





 = +











 =
=
τ
∂
∂
τ
∂
∂
τ
∂
∂
τ
∂
∂
∂
∂
τ
τ τ
ik
i
k
ik
i
k
ki
k
i
ik
i
k
k
i
ik ik
u
x
u
x
u
x
u
x
u
x
D
ik ki1
2
1
2
τ µ λ δik ik kk ikD D= +2
HENCE ( )Φ = = +τ µ λ δik ik ik kk ik ikD D D D2
OR
( )[ ] ( )[ ]
( )[ ] ( )
Φ = + + + + + + +
+ + + + + + + + + + ⇒
=
2 2
2 2
11 11 22 33 11 22 11 22 33 22
33 11 22 33 33 12
2
21
2
13
2
31
2
23
2
32
2
µ λ µ λ
µ λ µ
D D D D D D D D D D
D D D D D D D D D D D
D Dij ji
( ) ( )Φ = + + + + + + + +2 2 2 211
2
22
2
33
2
12
2
13
2
23
2
11 22 33
2
µ λD D D D D D D D DOR
SOLO
(2.6) CONSTITUTIVE RELATIONS
(2.6.1) NAVIER–STOKES EQUATIONS (CONTINUE)

62. 62
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6.1.3) COMPUTATION (CONTINUE)
USING STOKES ASSUMPTION: tr ~τ λ µ= ⇒ = −0
2
3
Φ
( ) ( )Φ = + + + + + + + +2 2 2 211
2
22
2
33
2
12
2
13
2
23
2
11 22 33
2
µ λD D D D D D D D D
( ) ( ) ( )
( )
( )

( )
Φ = + + − + + + + +
+ + + − + +
+ +
2
3
4
3
4
3
4
2
3
11 22 33
2
11 22 11 33 22 33 11
2
22
2
33
2
2
12
2
13
2
23
2
11 22 33
2
11
2
22
2
33
2
µ µ µ
µ
µ
λ
µ
D D D D D D D D D D D D
D D D D D D
D D D
  
OR
( ) ( ) ( )[ ] ( )Φ = − + − + − + + + >
2
3
4 011 22
2
11 33
2
22 33
2
12
2
13
2
23
2µ
µD D D D D D D D D
SOLO
(2.6) CONSTITUTIVE RELATIONS
(2.6.1) NAVIER–STOKES EQUATIONS (CONTINUE)

63. 63
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6.1.4) ENTROPY AND VORTICITY
From (C.L.M.)
or
( ) ( )[ ]Du
Dt
u
t
u
u u G p u u
 
    
= + ∇





 − × ∇ × = − ∇ − ∇ × ∇ × + ∇ + ∇ ⋅
∂
∂ ρ ρ
µ
ρ
λ µ
2
2
1 1 1
2
GIBBS EQUATION: T d s d h
d p
= −
ρ






∀





+⋅∇−





+⋅∇=





+⋅∇
→→→→
tld
pd
td
t
p
ldp
hd
td
t
h
ldh
sd
td
t
s
ldsT &
1
      
∂
∂
ρ∂
∂
∂
∂
Since this is true for d l t
→
&
T s h
p
T
s
t
h
t
p
t
∇ = ∇ −
∇
= −
ρ
∂
∂
∂
∂ ρ
∂
∂
&
1
SOLO
(2.6) CONSTITUTIVE RELATIONS
(2.6.1) NAVIER–STOKES EQUATIONS (CONTINUE)
Josiah Willard Gibbs
(1903 – 1839)

64. 64
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6.1.4) ENTROPY AND VORTICITY
from (C.L.M.)
or
GIBBS EQUATION: T d s d h
d p
= −
ρ






∀





+⋅∇−





+⋅∇=





+⋅∇
→→→→
tld
pd
td
t
p
ldp
hd
td
t
h
ldh
sd
td
t
s
ldsT &
1
      
∂
∂
ρ∂
∂
∂
∂
Since this is true for all d l t
→
&
T s h
p
T
s
t
h
t
p
t
∇ = ∇ −
∇
= −
ρ
∂
∂
∂
∂ ρ
∂
∂
&
1
SOLO
hsTG
p
Guuu
t
u
II
III
II
I
,,
,,,
,
2
,
~~
2
1
∇−∇+
⋅∇
+=
⋅∇
+
∇
−=








×∇×−





∇+
ρ
τ
ρ
τ
ρ∂
∂ 

ρ
p
hsT
dlpdp
dlhdh
dlsds
∇
−∇=∇→














⋅∇=
⋅∇=
⋅∇=

65. 65
Luigi Crocco
1909-1986
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6.1.4) ENTROPY AND VORTICITY (CONTINUE)
Define
Let take the CURL of this equation
Vorticityu

×∇≡Ω
If , then from (C.L.M.) we get:

G = −∇Ψ
CRROCO’s EQUATION (1937)
 ( ) ( )






⋅∇×∇+





Ψ++∇×∇−∇×∇=×Ω×∇+×∇
Ω
τ
ρ∂
∂ ~1
0
2
2
  


u
hsTuu
t
SOLO
ρ
τ
∂
∂ ~
2
1 ,2
,,
⋅∇
+





Ψ++∇−∇=×Ω+
I
II
I
uhsTu
t
u 
hsTGuuu
t
u
II
I
II
I
,,
,
,
2
,
~
2
1
∇−∇+
⋅∇
+=








×∇×−





∇+
ρ
τ
∂
∂ 

From

66. 66
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6.1.4) ENTROPY AND VORTICITY (CONTINUE)
( ) ( ) ( ) ( ) ( )∇ × × = ⋅∇ − ∇ ⋅ + ∇ ⋅ − ⋅∇ ← ∇ ⋅ = ∇ ⋅∇ × =
    

       
Ω Ω Ω Ω Ω Ωu u u u u u
0
0
( )∇ × ∇ = ∇ × ∇T s T s
τ
ρ
τ
ρ
τ
ρ
~
0
1~1~1
⋅∇×∇+⋅∇×





∇=






⋅∇×∇ 
Therefore ( ) ( ) ( ) τ
ρ∂
∂ ~1
⋅∇×





∇−∇×∇=∇⋅Ω−Ω⋅∇+Ω∇⋅+
Ω
sTuuu
t


SOLO
( ) ( ) τ
ρ
~1
⋅∇×





∇−∇×∇+⋅∇Ω−∇⋅Ω=
Ω
sTuu
tD
D 

or

67. 67
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6) CONSTITUTIVE RELATIONS
(2.6.1) NAVIER–STOKES EQUATIONS (CONTINUE)
(2.6.1.4) ENTROPY AND VORTICITY (CONTINUE)
( ) ( ) τ
ρ
~1
⋅∇×





∇−∇×∇+⋅∇Ω−∇⋅Ω=
Ω
sTuu
tD
D 

FLUID WITHOUT VORTICITY WILL REMAIN FOREVER WITHOUT
VORTICITY IN ABSENSE OF ENTROPY GRADIENTS OR VISCOUS
FORCES
- FOR AN INVISCID FLUID ( )λ µ τ= = → =0 0~ ~
( ) ( ) sTuu
tD
D
INVISCID
∇×∇+⋅∇Ω−∇⋅Ω=
Ω = 

0
~~τ
- FOR AN HOMENTROPIC FLUID
INITIALLY AT REST
s const everywhere i e s
s
t
. ; . . &∇ = =





0 0
∂
∂( )( )
 
Ω 0 0=
( )
D
Dt
s

   Ω
Ω= = = ∇ =0 0 0 0 0~ ~
, ,τ
SOLO
Return to Table of Content

68. 68
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6) CONSTITUTIVE RELATIONS
(2.6.2) STATE EQUATION
p - PRESSURE (FORCE / SURFACE)
V - VOLUME OF GAS
M - MASS OF GAS
R - 8314
- 286.9
T - GAS TEMPERATURE
- GAS DENSITY
[ ]m3
[ ]kg
[ ]J kg mol Ko
/ ( )⋅
[ ]J kg Ko
/ ( )⋅R
[ ]kgmol /−η
[ ]o
K
[ ]kg m/ 3
ρ
[ ]2
/ mN
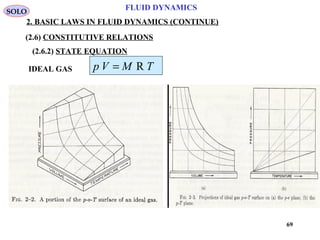
IDEAL GAS
TRMVp η=
TMVp R=
DEFINE: ρ
ρ
= = =
∆ ∆M
V
v
V
M
&
1
pv T= R
p T= ρ R
OR
SOLO

69. 69
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
IDEAL GAS TMVp R=
SOLO
(2.6) CONSTITUTIVE RELATIONS
(2.6.2) STATE EQUATION

70. 70
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
VAN DER WAALS (1873)
EQUATION
ARISE FROM THE EXISTENCE
OF INTERNAL FORCES BETWEEN
GAS MOLECULES
REAL GAS
( ) TRbv
v
a
p =−





+ 2
2
/ va
IS PROPORTIONAL TO THE
VOLUME OCCUPIED BY THE
GAS MOLECULES THEMSELVES
b
( )
070.15100
488.01400
686.0920
510.0350
587.0344
427.08.62
372.057.8
2
2
2
2
3
2
6
Hg
OH
CO
O
Air
H
He
molelbm
ft
molelbm
ftatm
baGAS






−





−
⋅
SOLO
(2.6) CONSTITUTIVE RELATIONS
(2.6.2) STATE EQUATION

71. 71
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
VAN DER WAALS
(1873) EQUATION
REAL GAS ( ) TRbv
v
a
p =−





+ 2
SOLO
(2.6) CONSTITUTIVE RELATIONS
(2.6.2) STATE EQUATION
Return to Table of Content

72. 72
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6) CONSTITUTIVE RELATIONS
(2.6.3) THERMALLY PERFECT GAS AND CALORICALLLY PERFECT GAS
A THERMALLY PERFECT GAS IS DEFINED AS A GAS FOR WHICH THE
INTERNAL ENERGY e IS A FUNCTION ONLY OF THE TEMPERATURE T.
( ) ( )h e T p e T RT h T= + = + =/ ( )ρ THERMALLY PERFECT GAS
DEFINE
C
C
v
V V
p
p p p p
e
T
q
T
h
T
de pdv v d p
d T
de pdv
d T
dq
d T
= =
= = = =


















+ +





+











∆
∆
∂
∂
∂
∂
∂
∂
A CALORICALLY PERFECT GAS IS DEFINED AS A GAS FOR WHICH
IS CONSTANT
Cv
CALORICALLY PERFECT GASe C Tv=
SOLO

73. 73
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6) CONSTITUTIVE RELATIONS
(2.6.3) CALORICALLLY PERFECT GAS (CONTINUE)
A CALORICALLY PERFECT GAS IS DEFINED AS A GAS FOR WHICH
IS CONSTANT
Cv
CALORICALLY PERFECT GASe C Tv=
FOR A CALORICALLY PERFECT GAS
( )h C T RT C R T C T C C Rv v p p v= + = + = → = +
γ
γ
γ γ
= ⇒ =
−
⇒ =
−
= + = −∆ C
C
C R C
Rp
v
C C R
p
R C C
v
p v p v
1 1
γ air = 14.
SOLO

74. 74
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6) CONSTITUTIVE RELATIONS
(2.6.3) CALORICALLLY PERFECT GAS (CONTINUE)
(2.6.3.1) ENTROPY CALCULATIONS FOR A CALORICALLLY PERFECT GAS
pv T= R p T= ρ R IDEAL GAS
( )
ds
de pdv
T
de pdv vdp vdp
T
dh vdp
T
=
+
=
+ + −
=
−∆
ds C
dT
T
R
dv
v
s s C
T
T
R
v
v
C
T
T
Rv v v= + → − = + = −2 1
2
1
2
1
2
1
2
1
ln ln ln ln
ρ
ρ
1
2
1
2
12 lnln
p
p
R
T
T
Css
p
dp
R
T
dT
Cds pp −=−→−=
s s C
p
p
R C
p
p
Cv v p2 1
2
1
1
2
2
1
2
1
2
1
− = ⋅





 − = −ln ln ln ln
ρ
ρ
ρ
ρ
ρ
ρ
ENTROPY
SOLO

75. 75
FLUID DYNAMICS
2. BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
(2.6) CONSTITUTIVE RELATIONS
(2.6.3) CALORICALLLY PERFECT GAS (CONTINUE)
(2.6.3.1) ENTROPY CALCULATIONS FOR A CALORICALLLY PERFECT GAS
p
p
T
T
e
T
T
e
p
p
T
T
C
R s s
R
s s
R
isentropic
s s
p
2
1
2
1
2
1
1
2
1
2
1
12 1 2 1 2 1
=





 =





 =






−
− − −
− = −
⇒
γ
γ
γ
γ
ρ
ρ
ρ
ρ
γ
γ γ
2
1
2
1
2
1
1
1
2
1
2
1
1
12 1 2 1 2 1
=





 =





 =






−
− − −
− = −
⇒
T
T
e
T
T
e
T
T
C
R s s
R
s s
R
isentropic
s s
v
p
p
e e
p
p
C
C s s
R
s s
R
isentropic
s s
p
v
2
1
2
1
2
1
2
1
2
1
2 1 2 1 2 1
=





 =





 =






−
−
−
− =
⇒
ρ
ρ
ρ
ρ
ρ
ρ
γ γ
T
T
h
h
p
p
e
p
p
e
T
T
h
h
p
p
s s
C
s s
C
isentropic
s s
v p2
1
2
1
2
1
2
1
2
1
1
2
1
1
2
1
2
1
2
1
1
2
1
12 1 2 1
2 1
= = ⋅ =





 =





 = =





 =






−
−
−
− −
−
=
−
−
⇒
ρ
ρ
ρ
ρ
ρ
ρ
γ
γ
γ
γ
γ
γ
ISENTROPIC CHAIN
SOLO
Return to Table of Content

76. 76
FLUID DYNAMICS
BASIC LAWS IN FLUID DYNAMICS (CONTINUE)
BOUNDARY CONDITIONS
SOLO

77. 77
EXAMPLE: BASIC LAWS IN FLUID DYNAMICS
ρρ
pd
dp
md
Wd
dhdgud
V
d
fluid
shaft
−





−








=++




 1
2
2
(5) THE SECOND LAW OF THERMODYNAMICS
SOLO
Assume an isentropic process (ds = 0)
0=Qδ- no heat added
0=








fluid
loss
md
Wd
d- no losses
The First Law of Thermodynamics becomes
From Gibbs Law  0
1
0
=





+=
ρ
dpudsdT
Gibbs
Isentropic
Combine First Law of Thermodynamics with Gibbs Law, to obtain:
hdg
pdV
d
md
Wd
d
fluid
shaft
++





=








ρ2
2
Second Law of Thermodynamics for an isentropic process
FLUID DYNAMICS

78. 78
(5) THE SECOND LAW OF THERMODYNAMICS
SOLO
Assume an isentropic process (ds = 0)
hdg
pdV
d
md
Wd
d
fluid
shaft
++





=








ρ2
2
1. For an incompressible fluid (ρ = const, dρ = 0)
and integrate this equation
( ) ( ) ( )12
12
2
1
2
2
2
hhg
ppVV
md
Wd ltheoretica
ltheoreticafluid
shaft
−+
−
+
−
=








ρ
2. For a perfect gas and an isentropic process 







== const
pp
γγ
ρρ 1
1
hdg
pd
p
pV
d
md
Wd
d
fluid
shaft
+





+





=








−
1
/1
1
2
2 ρ
γ
( ) ( ) ( )12
1
1
1
1
1
2
1
/1
1
2
1
2
2
1
1
1
2
hhgpp
pVV
md
Wd ltheoretica
ltheoreticafluid
shaft
−+
−





 −+
−
=







 −−
γ
ρ
γγ
γ
( ) ( ) ( )12
1
1
1
2
1
/1
1
2
1
2
2
12
hhgpp
pVV ltheoretica
−+




 −
−
+
−
=
−−
γ
γ
γ
γ
γ
ργ
γ
11
1
1
1
1
1
/1
1
111
TcTR
p
p
p
p
=
−
=
−
=
−
−
γ
γ
ργ
γ
ργ
γ γ
γ
γ
( ) ( ) ( )12
1
1
2
1
2
1
2
2
1
2
hhg
p
p
Tc
VV
md
Wd
p
ltheoretica
ltheoreticafluid
shaft
−+










−





+
−
=








−
γ
γ
( ) ( ) ( )12
1
1
2
1
1
1
/1
1
2
1
2
2
1
12
hhg
p
p
p
pVV ltheoretica
−+










−





−
+
−
=
−
− γ
γ
γ
γ
γ
ργ
γ
FLUID DYNAMICS
EXAMPLE: BASIC LAWS IN FLUID DYNAMICS

79. 79
TURBOMACHINERY
EXAMPLE: EFFICIENCY OF A PUMP
SOLO
The efficiency is composed of three parts:
• Volumetric efficiency:
L
v
QQ
Q
+
=η
Loss of fluid due to leakage in the impeller-casing clearanceL
Q
• Hydraulic efficiency:
s
f
h
h
h
−=1η
1. Shock loss due to imperfect match between inlet flow and blade entrance
2. Friction loss
3. Circulation loss due to imperfect match at the exit side of the blade
has three parts:f
h
• Mechanic efficiency:
T
Pf
m
ω
η −=1
Power loss due to mechanical friction in the bearings, and other
contact points in the pump.
f
P
Total efficiency is :
mhv
ηηηη =:
Return to Table of Content

80. 80
SOLO
Dimensionless Equations
Dimensionless Variables are:
0/~ ρρρ = 0/
~
Uuu = gGG /
~
= ( )2
00/~ Upp ρ=
0/~ lUtt =
2
0/
~
UCTT p=( )2
00/~ Uρττ =
2
0/
~
UHH =
2
0/
~
Uhh =
2
0/~ Uee = ( )2
00/~ Uqq ρ= ( )2
/
~
UQQ =
∇=∇ 0
~
l
Field Equations
(C.M.): ( )
00
0
0
U
l
u
t ρ
ρ
∂
ρ∂
=⋅∇+

( ) 2
00
0
~
3
4
U
l
uupGuu
t
u
ρ
µµρ
∂
∂
ρ
τ
  


⋅∇






⋅∇∇+×∇×∇−∇−=





∇⋅+(C.L.M.):
( ) ( ) 3
00
0~
U
l
Tk
t
Q
uGu
t
p
Hu
t
H
q
ρ∂
∂
ρτ
∂
∂
ρ



∇⋅∇−+⋅+⋅⋅∇+=





∇⋅+
∂
∂
(C.E.):
( )
( )
( ) 0
/
/
00
0
00
0
=





⋅∇+
U
u
l
lUt

ρ
ρ
∂
ρρ∂
( )
( ) ( )
( ) ( ) 





⋅∇∇





+





×∇×∇





−
∇−=






∇⋅+
0
00
000
0
0
0
0
0
000
0
2
00
02
0
0
00
0
000
0
0
3
4
/
/
U
u
ll
UlU
u
ll
Ul
U
p
l
g
G
U
lg
U
u
l
U
u
lUt
Uu


ρ
µ
µ
µ
ρ
µ
ρρ
ρ
∂
∂
ρ
ρ
( ) ( )
( )
( )
( ) ( ) 







∇⋅∇














−+⋅+







⋅⋅∇+







∂
∂
=







2
0
0
0
0
0
0
000
0
2
00000
2
0
0
0
2
00
02
0000
2
00000 /
~
// U
CT
l
k
k
l
C
k
UlU
Q
lUtU
u
g
G
U
gl
U
u
U
l
U
p
lUtU
H
lUtD
D p
pµρ
µ
∂
∂
ρ
ρ
ρ
τ
ρρρ
ρ

0/~ ρρρ = 0/
~
Uuu = gGG /
~
= ( )2
00/~ Upp ρ=
0/~ lUtt =
2
0/
~
UCTT p=( )2
00/~ Uρττ =
2
0/
~
UHH =
2
0/
~
Uhh =
2
0/~ Uee = ( )2
00/~ Uqq ρ= ( )2
/
~
UQQ =
∇=∇ 0
~
l
0/~ µµµ =
0/
~
kkk =
Reference Quantities: ρ0(density), U0(velocity), l0 (length), g (gravity), μ0 (viscosity),
k0 (Fourier Constant), λ0 (mean free path)
0/
~
λλλ =

81. 81
SOLO
Dimensionless Equations
Dimentionless Field Equations
(C.M.): ( ) 0
~~~~
=⋅∇+ u
t

ρ
∂
ρ∂
( ) ( )u
R
u
R
pG
F
uu
t
u
eer
~~~~1
3
4~~~~1~~~~1~~~
~
~
~
2


⋅∇∇+×∇×∇−∇−=







∇⋅+ µµρ
∂
∂
ρ(C.L.M.):
( ) ( )Tk
PRt
Q
uG
F
u
t
p
Hu
t
H
rer
∇⋅∇−+⋅+⋅⋅∇+=







∇⋅+
∂
∂ 11
~
~
~~~1~~~
~
~~~~
~
~
~
2
∂
∂
ρτ
∂
∂
ρ

(C.E.):
Reynolds:
0
000
µ
ρ lU
Re = Prandtl:
0
0
k
C
P p
r
µ
= Froude:
0
0
gl
U
Fr =
0/~ ρρρ = 0/
~
Uuu = gGG /
~
= ( )2
00/~ Upp ρ=
0/~ lUtt =
2
0/
~
UCTT p=( )2
00/~ Uρττ =
2
0/
~
UHH =
2
0/
~
Uhh =
2
0/~ Uee = ( )2
00/~ Uqq ρ= ( )2
/
~
UQQ =
∇=∇ 0
~
l
0/~ ρρρ = 0/
~
Uuu = gGG /
~
= ( )2
00/~ Upp ρ=
0/~ lUtt =
2
0/
~
UCTT p=( )2
00/~ Uρττ =
2
0/
~
UHH =
2
0/
~
Uhh =
2
0/~ Uee = ( )2
00/~ Uqq ρ= ( )2
/
~
UQQ =
∇=∇ 0
~
l
0/~ µµµ =
0/
~
kkk =
Dimensionless Variables are:
Reference Quantities: ρ0(density), U0(velocity), l0 (length), g (gravity), μ0 (viscosity),
k0 (Fourier Constant), λ0 (mean free path)
0/
~
λλλ =
Knudsen
l
Kn
0
0
:
λ
=

82. 82
SOLO
Dimensionless Equations
Constitutive Relations
TRp ρ=
2
2
1
uTCH p +=
Tkq ∇−=

TCh p=





−
== 2
00
2
00
2
00
1
U
TC
U
TC
C
R
U
p pp
p ρ
ρ
γ
γ
ρ
ρ
ρ






=





2
0
2
0 U
TC
U
h p
2
0
2
0
2
0 2
1






+





=





U
u
U
TC
U
H p
( ) 





∇














−= 2
0
0
00
0
000
0
3
00 U
TC
l
k
k
C
k
UlU
q p
p µρ
µ
ρ

( ) [ ]3
3
2~ Iuuu T 
⋅∇−∇+∇= µµτ [ ]3
0
0
0000
0
0
0
0
0
0000
0
00 3
2~
I
U
u
l
UlU
u
l
U
u
l
UlU
T 
⋅∇





−





∇+∇





=
µ
µ
ρ
µ
µ
µ
ρ
µ
ρ
τ
0/~ ρρρ = 0/
~
Uuu = gGG /
~
= ( )2
00/~ Upp ρ=
0/~ lUtt =
2
0/
~
UCTT p=( )2
00/~ Uρττ =
2
0/
~
UHH =
2
0/
~
Uhh =
2
0/~ Uee = ( )2
00/~ Uqq ρ= ( )2
/
~
UQQ =
∇=∇ 0
~
l
0/~ ρρρ = 0/
~
Uuu = gGG /
~
= ( )2
00/~ Upp ρ=
0/~ lUtt =
2
0/
~
UCTT p=( )2
00/~ Uρττ =
2
0/
~
UHH =
2
0/
~
Uhh =
2
0/~ Uee = ( )2
00/~ Uqq ρ= ( )2
/
~
UQQ =
∇=∇ 0
~
l
0/~ µµµ =
0/
~
kkk =
Dimensionless Variables are:
Reference Quantities: ρ0(density), U0(velocity), l0 (length), g (gravity), μ0 (viscosity),
k0 (Fourier Constant), λ0 (mean free path)
0/
~
λλλ =

83. 83
SOLO
Dimensionless Equations
Dimensionless Constitutive Relations
2~
2
1~~
uTH +=
Tp
~~1~ ρ
γ
γ −
= Ideal Gas
( ) [ ]3
~~~
3
2~~~~~~~ Iu
R
uu
R e
T
e

⋅∇−∇+∇=
µµ
τ Navier-Stokes
Th
~~
= Calorically Perfect Gas
Tk
PR
q
re
~~~11~
∇−=
 Fourier Law
Reynolds:
0
000
µ
ρ lU
Re =
Prandtl:
0
0
k
C
P
p
r
µ
=
0/~ ρρρ = 0/
~
Uuu = gGG /
~
= ( )2
00/~ Upp ρ=
0/~ lUtt =
2
0/
~
UCTT p=( )2
00/~ Uρττ =
2
0/
~
UHH =
2
0/
~
Uhh =
2
0/~ Uee = ( )2
00/~ Uqq ρ= ( )2
/
~
UQQ =
∇=∇ 0
~
l
0/~ ρρρ = 0/
~
Uuu = gGG /
~
= ( )2
00/~ Upp ρ=
0/~ lUtt =
2
0/
~
UCTT p=( )2
00/~ Uρττ =
2
0/
~
UHH =
2
0/
~
Uhh =
2
0/~ Uee = ( )2
00/~ Uqq ρ= ( )2
/
~
UQQ =
∇=∇ 0
~
l
0/~ µµµ =
0/
~
kkk =
Dimensionless Variables are:
Reference Quantities: ρ0(density), U0(velocity), l0 (length), g (gravity), μ0 (viscosity),
k0 (Fourier Constant), λ0 (mean free path)
0/
~
λλλ =
Return to Table of Content

84. 84
SOLO
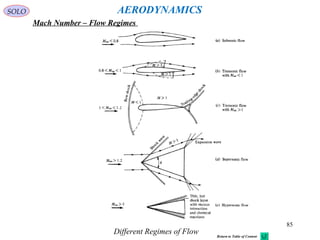
Mach Number
Mach number (M or Ma) / is a dimensionless quantity representing
the ratio of speed of an object moving through a fluid and the local
speed of sound.
• M is the Mach number,
• U0 is the velocity of the source relative to the medium, and
• a0 is the speed of sound
Mach:
0
0
a
U
M =
The Mach number is named after Austrian physicist and philosopher
Ernst Mach, a designation proposed by aeronautical engineer Jakob
Ackeret.
Ernst Mach
(1838–1916)
Jakob Ackeret
(1898–1981)
m
Tk
Mo
TR
a Bγγ
==0
• R is the Universal gas constant, (in SI, 8.314 47215 J K−1
mol−1
), [M1
L2
T−2
θ−1
'mol'−1
]
• γ is the rate of specific heat constants Cp/Cv and is dimensionless
γair = 1.4.
• T is the thermodynamic temperature [θ1
]
• Mo is the molar mass, [M1
'mol'−1
]
• m is the molecular mass, [M1
]
AERODYNAMICS

85. 85
SOLO
Different Regimes of Flow
Mach Number – Flow Regimes
AERODYNAMICS
Return to Table of Content

86. 86
where
ρ = air density
V = true speed
l = characteristic length
μ = absolute (dynamic) viscosity
υ = kinematic viscosity
Reynolds:
υµ
ρ ρ
µ
υ
lVlV
Re
=
==
Osborne Reynolds
(1842 –1912)
It was observed by Reynolds in 1884 that a Fluid Flow changes from Laminar to
Turbulent at approximately the same value of the dimensionless ratio (ρ V l/ μ) where l is
the Characteristic Length for the object in the Flow. This ratio is called the Reynolds
number, and is the governing parameter for Viscous Flow.
Reynolds Number and Boundary Layer
SOLO
1884AERODYNAMICS

87. 87
Boundary Layer
SOLO
1904AERODYNAMICS
Ludwig Prandtl
(1875 – 1953)
In 1904 at the Third Mathematical Congress, held at
Heidelberg, Germany, Ludwig Prandtl (29 years old) introduced
the concept of Boundary Layer.
He theorized that the fluid friction was the cause of the fluid
adjacent to surface to stick to surface – no slip condition, zero
local velocity, at the surface – and the frictional effects were
experienced only in the boundary layer a thin region near the
surface. Outside the boundary layer the flow may be considered
as inviscid (frictionless) flow.
In the Boundary Layer on can calculate the
•Boundary Layer width
•Dynamic friction coefficient μ
•Friction Drag Coefficient CDf

88. 88
The flow within the Boundary Layer can be of two types:
•The first one is Laminar Flow, consists of layers of flow sliding one over other in a
regular fashion without mixing.
•The second one is called Turbulent Flow and consists of particles of flow that
moves in a random and irregular fashion with no clear individual path, In
specifying the velocity profile within a Boundary Layer, one must look at the
mean velocity distribution measured over a long period of time.
There is usually a transition region between these two types of Boundary-Layer Flow
SOLO AERODYNAMICS

89. 89
Normalized Velocity profiles within a Boundary-Layer, comparison between
Laminar and Turbulent Flow.
SOLO
Boundary-Layer
AERODYNAMICS

90. 90
Flow Characteristics around a Cylindrical Body
as a Function of Reynolds Number (Viscosity)
AERODYNAMICS
SOLO

91. 91
Relative Drag Force as a Function of Reynolds Number (Viscosity)
AERODYNAMICS
Drag CD0 due to
Flow Separation
SOLO
Return to Table of Content

92. 92
STEADY QUASI ONE-DIMENSIONAL FLOWSOLO
u
p
ρ
T
e
1
1
1
1
1
1 2
u
p
ρ
e
2
2
2
2
T 2
A 2 1x1x- A 1
q
Q
τ 11
A 3
( )
( )
0
0
0..
=+⇒





−==
+==
ρ
ρ
dp
ududp
dhTdsisentropic
ududhdHEC



⇔
⇔
⇒−=
increaseudecreasep
decreaseuincreasep
u
du
dp
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρρ
d
M
d
u
ad
d
dp
u
dp
uu
du
ds
22
2
0
22
111
−=−=





−=−=
=
( )







=++
−=
0..
2
A
dA
u
dud
MC
u
du
M
d
ρ
ρ
ρ
ρ
( )
( ) 


















−=−=





 −
−−=−=→=
−=
−
==→
u
du
M
Mu
du
M
A
dA
u
du
u
du
a
da
u
du
M
dM
a
u
M
d
u
du
M
a
dad
p
dp
isentropic
2
2
2
2
1
11
2
1
1
2
γ
ρ
ρ
γ
γ
ρ
ρ
γ
( ) u
du
M
d
u
du
A
dA
12
−=−−=
ρ
ρ
M
dM
M
M
A
dA
p
dp
MA
dA
2
2
2
2
1
1
1
1
1
1
−
+
−
=






−−=
γ
γ
Steady , Adiabatic + Inviscid = Reversible, , ( )
q Q= =0 0, ( )~ ~
τ = 0 ( )
 
G = 0
∂
∂ t
=





0

93. 93
STEADY QUASI 1-DIMENSIONAL GASESSOLO
( ) M
dM
M
M
p
dp
M
d
Mu
du
M
d
u
du
A
dA
2
2
22
2
2
1
1
11
1
11
11
−
+
−
=





−−=





−=−=−−=
γγρ
ρ
ρ
ρ
u increase
p decrease
p increase
u decrease
p increase
u decrease
u increase
p decrease
0>dA0<dA
1<M
1>M
(1) At M=0 decrease in A gives a
proportional
increase in velocity u
du
A
dA
−=
(2) For 0 < M < 1 the relation between A and
u is the same as for incompressible flow.
FLOW IN CONVERGING/DIVERGING DUCTS
(3) For M > 1 increase in A increases u .
Explanation: When M > 1 , ρ increases
faster than u, so A must increase to keep
constAum == ρ
(4) M = 1 can be attained only at throat.
Steady , Adiabatic + Inviscid = Reversible, , ( )
q Q= =0 0, ( )~ ~
τ = 0 ( )
 
G = 0
∂
∂ t
=





0

94. 94
STEADY QUASI ONE-DIMENSIONAL FLOWSOLO
STAGNATION CONDITIONS
(C.E.)
constuhuh =+=+ 2
22
2
11
2
1
2
1
The stagnation condition 0 is attained by reaching u = 0
2
/
21202
020
2
1
1
1
2
1
2
1
22
1
2
M
TR
u
Tc
u
T
T
c
u
TTuhh
TRa
auM
Rc
pp
Tch p
p
−
+=
−
+=+=→+=→+=
=
=
−
=
=
γ
γ
γ
γγ
γ
Using the Isentropic Chain relation, we obtain:
2
1
0102000
2
1
1 M
p
p
a
a
h
h
T
T −
+=





=





=





==
−
−
γ
ρ
ρ γ
γ
γ
Steady , Adiabatic + Inviscid = Reversible, , ( )
q Q= =0 0, ( )~ ~
τ = 0 ( )
 
G = 0
∂
∂ t
=





0

95. 95
STEADY QUASI ONE-DIMENSIONAL FLOWSOLO
CRITICAL CONDITIONS
An ideal gas flows from an
infinite reservoir
000
,,,0 ρρ ==== ppTTu
through a duct with variable
area A. The area A* at which
the flow reaches the sound
velocity u*=a* is called
critical area.
2
1
*****
1
0102000
+
=





=





=





==
−
−
γ
ρ
ρ γ
γ
γ
p
p
a
a
h
h
T
T2
1
0102000
2
1
1 M
p
p
a
a
h
h
T
T −
+=





=





=





==
−
−
γ
ρ
ρ γ
γ
γ
1=
⇒
M

( )12
1
2
1
1
2
2
1
2
0
0
**
0
0
/1 2
1
2
1
1
1
*
2
1
2
1
1
2
1
2
1
1
1
*
**
*
**
*
−
+
−
=












+
−
+
=












+
−
+












+
−
+
=





























=











=
γ
γ
γ
γ
γ
γ
γ
γ
γ
ρ
ρ
ρ
ρ
ρ
ρ
M
M
A
MM
M
A
a
a
a
a
u
a
A
u
u
AA
auM

(C.M.) *** AuAum ρρ ==
Steady , Adiabatic + Inviscid = Reversible, , ( )
q Q= =0 0, ( )~ ~
τ = 0 ( )
 
G = 0
∂
∂ t
=





0

96. 96
STEADY QUASI ONE-DIMENSIONAL FLOW
H h
u
C T
u p u a u
constp
C R
t
p
= + = + =
−
+ =
−
+ =
=
−
=
2 2 1
0
0
2 2 2
0
2 2 1 2 1 2
γ
γ
∂
∂
γ
γ ρ γ
a RT
p
≡ =γ γ
ρ
M
u
a
M
u
a
≡
≡∗
∗
H C T
u
C T
p a
p p= + ≡
=
−
=
−
2
0
0
0
0
2
2
1 1
γ
γ ρ γ
(1)Stagnation point
on a path:
The gas is brought
(imaginary) by an
adiabatic process to
the rest: u = 0
a
a
R T
R T
R
C
u
R T
M
p
0
2
0
2
2
1
2
1
1
2





 =
= + ⇒
= +
−
γ
γ
γ
γ
γ
⇒
=
=−
+
−
+
==




 1
2
2
2
1
1
2
2
1
2
1
2
2
1
1
2
1
1 M
MM
M
M
T
T
a
a
γ
γ
T
T
M
∗ =
+
+
−
⇒
γ
γ
1
2
1
1
2
2
T
T
a
a
∗ ∗ =
=





 =
+
=
0 0
2
1 4
2
1
0833
γ
γ .
.
( ) ( )
( )
a u a a
a
2 2
2 2
2
1 2 1 2
1
1 2
γ γ
γ
γ
−
+ =
−
+
=
+
−
∗ ∗
∗
( )
( )
( ) ( )
⇒ =
+
+ −
⇓
=
+ − −
∗
∗
∗
M
M
M
M
M
M
2
2
2
2
2
2
1
2 1
2
1 1
γ
γ
γ γ
M* - Characterisic Mach Number
H H1 2
=
(2)Any two points
1and 2 where
are related by:
(3)The gas is brought
(imaginary) by an
adiabatic process
to
u* = a*
Alternative Forms of the Quasi One-Dimensional Energy Equation and Definition of Reference Quantities
u
p
ρ
T
e
1
1
1
1
1
1 2
u
p
ρ
e
2
2
2
2
T 2
A 2 1x1x-A 1
q
Q
τ 11
A 3
Steady , Adiabatic + Inviscid = Reversible, , ( )
q Q= =0 0, ( )~ ~
τ = 0 ( )
 
G = 0
Ideal and Calorically Perfect Gas (1). ( )p R T= ρ ( )h C Tp=
∂
∂ t
=





0
SOLO

97. 97
STEADY QUASI ONE-DIMENSIONAL FLOW
(1)Stagnation point
on a path:
The gas is brought
(imaginary) by an
adiabatic process to
the rest: u = 0
H H1 2
=
(2)Any two points
1and 2 where (3)The gas is brought
(imaginary) by an
adiabatic process
to
u* = a*
p
p
T
T
True on same path
1
2
1
2
1
2
1
=





 =






−ρ
ρ
γ
γ
γ
  
Isentropic Chain
0.1 1 10
M
T
T0
p
p0
ρ
ρ 0
1
p
p
M0 2
1
1
1
2
= +
−





−γ
γ
γ
p
p
M
M
2
1
1
2
2
2
1
1
1
2
1
1
2
=
+
−
+
−










−γ
γ
γ
γ
p
p
M
∗
−
=
+
+
−










γ
γ
γ
γ1
2
1
1
2
2
1
p
p
∗ − =
=
+





 =
0
1 1 4
2
1
0528
γ
γ
γ γ .
.
ρ
ρ
γ γ
0 2
1
1
1
1
2
= +
−





−
M
ρ
ρ
γ
γ
γ
2
1
1
2
2
2
1
1
1
1
2
1
1
2
=
+
−
+
−










−
M
M
ρ
ρ
γ
γ
γ
∗
−
=
+
+
−










1
2
1
1
2
2
1
1
M
ρ
ρ γ
γ γ∗ − =
=
+





 =
0
1
1 1 4
2
1
0 6339
.
.
Mollier’s Diagram
u
p
ρ
T
e
1
1
1
1
1
1 2
u
p
ρ
e
2
2
2
2
T 2
A 2 1x1x-A 1
q
Q
τ 11
A 3
Steady , Adiabatic + Inviscid = Reversible, , ( )
q Q= =0 0, ( )~ ~
τ = 0 ( )
 
G = 0
Ideal and Calorically Perfect Gas (2). ( )p R T= ρ ( )h C Tp=
∂
∂ t
=





0
Alternative Forms of the Quasi One-Dimensional Energy Equation and Definition of Reference Quantities
SOLO
are related by:

98. 98
STEADY QUASI ONE-DIMENSIONAL FLOWSOLO
ISENTROPIC SUPERSONIC NOZZLE FLOW (1)
Assume that the gas
in a large container
at rest
0,,, 0000 =uTp ρ
The gas is released
trough an diverging/
converging duct to
a second container
in which the pressure
is regulated with a
pump such that
1
2
0
0
2
1
1
−





 −
+
=
γ
γ
γ
M
p
pB
u
p
ρ
T
e
1
1
1
1
1
1 2
u
p
ρ
e
2
2
2
2
T 2
A 2 1x1x-A 1
q
Q
τ 11
A 3

99. 99
STEADY QUASI ONE-DIMENSIONAL FLOWSOLO
ISENTROPIC SUPERSONIC NOZZLE FLOW (2)
Assume that the gas
in a large container
at rest
0,,, 0000 =uTp ρ
To fit the pressure at
the output a shock
wave increases the
pressure by a jump.
the Mach number
jumps from
Supersonic to
Subsonic.
1
2
0
0
2
1
1
−





 −
+
=≠
γ
γ
γ
M
p
pp BBi
the pressure in the
second container.
Bip
u
p
ρ
T
e
1
1
1
1
1
1 2
u
p
ρ
e
2
2
2
2
T 2
A 2 1x1x-A 1
q
Q
τ 11
A 3

100. 100
STEADY QUASI ONE-DIMENSIONAL FLOWSOLO
ISENTROPIC SUPERSONIC NOZZLE FLOW (3)
In this case the duct
between the two
containers has no
throat, therefore a
shock wave is not
possible.
u
p
ρ
T
e
1
1
1
1
1
1 2
u
p
ρ
e
2
2
2
2
T 2
A 2 1x1x-A 1
q
Q
τ 11
A 3
Assume that the gas
in a large container
at rest
0,,, 0000 =uTp ρ
the pressure in the
second container.
Bip
No Throat

101. 101
STEADY ONE-DIMENSIONAL FLOW EQUATIONS
SOLO
Steady , 1-D Flow ,Adiabatic, ,
∂
∂ t
=





0
( )0=Q ( )
 
G = 0
Ideal and Calorically Perfect Gas.( )p R T= ρ ( )h C Tp=






== 0
32 xx ∂
∂
∂
∂
Field Equations:

 ρ
∂
∂
ρ
∂
∂
ρ
∂
∂
∂τ
∂
τ
u
t
u
const
u
x
G
p
x x
M u p P
0
01
1
1
11
1
11+ = − + ⇒ + − =

 ( )   EquMHQuGqu
xx
H
u
t
H
M
=+−⇒++−=+ 11111
11
00
0
τρτ
∂
∂
∂
∂
ρ
∂
∂
ρ
No.
Equations Unknowns Knowns
1 ρ,u M
Pp 11,1 τ
1 H q E,
1 T
1
1
1
7Eq. 7Unknowns

( )

( ) Muu
xt
u
t
=⇒+==⋅∇+ ρρ
∂
∂
∂
ρ∂
ρ
∂
ρ∂
1
0
0
0

(C.M.)
ρ ρ τ
Du
Dt
G p


= −∇ + ∇⋅ ~ ~τ
τ
τ
τ
=










11
22
33
0 0
0 0
0 0
(C.L.M.)
( )ρ
∂
∂
τ ρ
D H
Dt
p
t
u G u q Q= + ∇⋅ ⋅ + ⋅ −∇⋅ +~     ~τ
τ
τ
τ
⋅ =





















u
u11
22
33
10 0
0 0
0 0
0
0
(C.E.)
Constitutive Relations
TRp ρ=Ideal Gas
H h u C T up= + = +
1
2
1
2
2 2
h C Tp=Calorically Perfect
q K
T
x
= −
∂
∂ 1
Fourier
Conduction Law
τ µ
∂
∂
11
1
4
3
=
u
x
τ τ µ
∂
∂
22 33
1
2
3
= = −
u
x
τ τ τ
τ τ
τ τ
τ τ
11 22 33
12 21
13 31
32 23
0
0
0
0
+ + =
= =
= =
= =







Newtonian Flow
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2

102. 102
SOLO
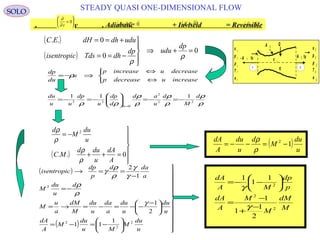
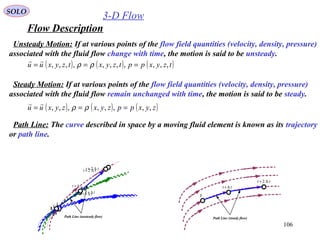
Steady One-Dimensional Flow
∂
∂ t
=





0
∂
∂
∂
∂x x2 3
0= =






Flow between two Equilibrium States (1) and (2)
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
Q
1
1
1
1
1
2
2
2
2
2
1 2
τ µ
∂
∂
∂
∂
µ
∂
∂
δik
i
k
k
i
k
k
ik
u
x
u
x
u
x
= +





 −
2
3
Assume Newtonian fluid (Navier-Stokes Eq.) in each state
( ) ( )
τ µ
∂
∂
τ τ µ
∂
∂
∂
∂
∂
∂
11
1
1
22 33
1
1
1
1 2
1
4
3
2
3
0
=
= =−
=−










⇐ =
⇔
u
x
u
x
q K
T
x
x
equilibrium
We obtain
Let integrate the field equations between state (1) and state (2)
[ ]ρu
1
2
0=
[ ] 
ρ τ ρu p G dx2
1
2
12
1
2
1
1
2
0
+ − = ∫
[ ]   ( )ρ τ ρuH q u G u Q dx1
2
11
1
2
1
1
2
0 0
+ −








= +∫
No. Equations Unknowns Knowns
ρ2 2,u ρ1 1,u1
1
1
p2
p G1 1,
H2 H1
3 4
STEADY ONE-DIMENSIONAL FLOW EQUATIONS

103. 103
SOLO
Steady One-Dimensional Flow
∂
∂ t
=





0
∂
∂
∂
∂x x2 3
0= =






Flow between two Equilibrium States (1) and (2)
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
Q
1
1
1
1
1
2
2
2
2
2
1 2
ρ ρ1 1 2 2u u=
⇒
We need one more equation to solve the algebraic equations
Normal Shock Wave ( Adiabatic)
 
G Q= =0 0,
η
ρ
ρ
= =2
1
1
2
u
u
2
2
221
2
11 pupu +=+ ρρ
⇒
H H h u h u1 2 1 1
2
2 2
21
2
1
2
= → + = + ⇒
( )η
ρ
−+= 11
1
1
2
1
1
2
p
u
p
p
h
h
u
h
2
1
1
2
1
2
1
2
1
1
= + −






η
p 2 p 1
h 2 h 1
η
η
General iterative solution:
p
p
u
p
h
h
u
h
2
1
1
2
1
1
2
1
1
2
1
1 1
2
= + = +
ρ
,
(1)Choose η → ∞
(2)Go to Mollier Diagram ρ2
Compute η
ρ
ρ
= =2
1
1
2
u
u
(3)Go to ( ) 





−+=−+= 2
1
2
1
1
2
1
1
2
1
1
2 1
1
2
1,11
η
η
ρ
h
u
h
h
p
u
p
p
h 2
p2
ρ2
lg h
R
lg s
R
pC
1
vC
1
Mollier Diagram
Since we didn’t use
Constitutive Relations this is
True for all gases
STEADY ONE-DIMENSIONAL FLOW EQUATIONS
Richard Mollier
(1863 – 1935)

104. 104
SOLO
Steady , Adiabatic + Inviscid = Reversible, , ( )
q Q= =0 0, ( )~ ~
τ = 0 ( )
 
G = 0
COMPARISON OF ISENTROPIC (ds=0) AND
ADIABATIC (Q=0,q=0) FLOW PROCESSES
∂
∂ t
=





0
Return to Table of Content

105. 105
AERODYNAMICS
Fluid flow is characterized by a velocity vector field in
three-dimensional space, within the framework of
continuum mechanics. Streamlines, Streaklines and
Pathlines are field lines resulting from this vector field
description of the flow. They differ only when the flow
changes with time: that is, when the flow is not steady.
• Streamlines are a family of curves that are
instantaneously tangent to the velocity vector of the
flow. These show the direction a fluid element will
travel in at any point in time.
• Streaklines are the locus of points of all the fluid
particles that have passed continuously through a
particular spatial point in the past. Dye steadily injected
into the fluid at a fixed point extends along a streakline
• Pathlines are the trajectories that individual fluid particles follow. These can be thought of as
a "recording" of the path a fluid element in the flow takes over a certain period. The direction
the path takes will be determined by the streamlines of the fluid at each moment in time.
• Timelines are the lines formed by a set of fluid particles that were marked at a previous
instant in time, creating a line or a curve that is displaced in time as the particles move.
The red particle moves in a flowing fluid; its pathline is
traced in red; the tip of the trail of blue ink released from
the origin follows the particle, but unlike the static pathline
(which records the earlier motion of the dot), ink released
after the red dot departs continues to move up with the flow.
(This is a streakline.) The dashed lines represent contours of
the velocity field (streamlines), showing the motion of the
whole field at the same time. (See high resolution version.
Flow Description
SOLO

106. 106
3-D Flow
Flow Description
SOLO
Steady Motion: If at various points of the flow field quantities (velocity, density, pressure)
associated with the fluid flow remain unchanged with time, the motion is said to be steady.
( ) ( ) ( )zyxppzyxzyxuu ,,,,,,,, === ρρ

Unsteady Motion: If at various points of the flow field quantities (velocity, density, pressure)
associated with the fluid flow change with time, the motion is said to be unsteady.
( ) ( ) ( )tzyxpptzyxtzyxuu ,,,,,,,,,,, === ρρ

Path Line: The curve described in space by a moving fluid element is known as its trajectory
or path line.
tt
tt ∆+
t
tt ∆+
tt ∆+ 2
t
tt ∆+
tt ∆+ 2
Path Line (steady flow)
t
tt ∆+
t
tt ∆+ 2
tt ∆+
t
Path Line (unsteady flow)
tt ∆+ 2
tt ∆+
t

107. 107
3-D Flow
Flow Description
SOLO
Path Line: The curve described in space by a moving fluid element is known as its trajectory
or path line.
t
tt ∆+ tt ∆+ 2
Streamlines: The family of curves such that each curve is tangent at each point to the
velocity direction at that point are called streamlines.
Consider the coordinate of a point P and the direction of the streamline passing
through this point. If is the velocity vector of the flow passing through P at a time t,
then and parallel, or:
r
 rd
u

u

rd
0=×urd

( )
( )
( )
0
1
1
1111
=












−
−
−
=
zdyudxv
ydxwdzu
xdzvdyw
wvu
dzdydx
zyx
w
zd
v
yd
u
xd
==
Cartesian
t
u

r

rd

108. 108
3-D Flow
Flow Description
SOLO
Path Line: The curve described in space by a moving fluid element is known as its trajectory
or path line.
Streamlines: The family of curves such that each curve is tangent at each point to the
velocity direction at that point are called streamlines.
( ) ( ) ( )tzyxw
zd
tzyxv
yd
tzyxu
xd
,,,,,,,,,
==
t
u

r

rd
Those are two independent differential equations for a streamline. Given a point
the streamline is defined from those equations.( )0000 ,,, tzyxr

( )
( ) ( )
( )
( ) ( )tzyxw
zd
tzyxv
yd
tzyxv
yd
tzyxu
xd
,,,,,,
2
,,,,,,
1
=
=
( ) ( ) ( )
( ) ( ) ( ) 0,,,,,,,,,
0,,,,,,,,,
222
111
=++
=++
zdtzyxcydtzyxbxdtzyxa
zdtzyxcydtzyxbxdtzyxa
( ) ( )
( ) ( )21
21
22
11
•+•
•+•
βα
βα
0
22
11
≠
βα
βα
Pfaffian Differential Equations
For a given a point the solution of those equations is of the form:( )0000 ,,, tzyxr

( )
( ) 2,,,
1,,,
02
01
consttzyx
consttzyx
=
=
ψ
ψ
u

( )0
tr

rd
0t
( ) 11 cr =

ψ
( ) 22 cr =

ψ
Streamline
Those are two surfaces, the
intersection of which is the
streamline.

109. 109
3-D Flow
Flow Description
SOLO
Path Line: The curve described in space by a moving fluid element is known as its trajectory
or path line.
Streamlines: The family of curves such that each curve is tangent at each point to the
velocity direction at that point are called streamlines.
( ) ( ) ( )tzyxw
zd
tzyxv
yd
tzyxu
xd
,,,,,,,,,
==
t
u

r

rd
For a given a point the solution of those equations is of the form:( )0000 ,,, tzyxr

( )
( ) 2,,,
1,,,
02
01
consttzyx
consttzyx
=
=
ψ
ψ
u

( )0
tr

rd
0
t
( ) 11 cr =

ψ
( ) 22 cr =

ψ
Streamline
Those are two surfaces, the
intersection of which is the
streamline.
The streamline is perpendicular to the gradients (normals) of those two surfaces.
( ) ( ) ( )0201 ,, trtrVr

ψψµ ∇×∇=
where μ is a factor that must satisfy the following constraint.
( )( ) ( ) ( ) 0,, 0201 =∇×∇⋅∇=⋅∇ trtrVr

ψψµ
Return to Table of Content

110. 110
AERODYNAMICS
Streamlines, Streaklines, and Pathlines
Mathematical description
Streamlines
If the components of the velocity are written and those of the streamline as
we deduce
which shows that the curves are parallel to the velocity vector
Pathlines
Streaklines
where, is the velocity of a particle P at location and time t . The parameter , parametrizes the
streakline and 0 ≤ τP ≤ t0 , where t0 is a time of interest .
The suffix P indicates that we are following the motion of a fluid particle. Note that at point
the curve is parallel to the flow velocity vector where the velocity vector is evaluated at
the position of the particle at that time t .
SOLO

111. 111
∞V
Airfoil Pressure Field variation with α
AERODYNAMICS
Airfoil Velocity Field variation with αAirfoil Streamline variation with αAirfoil Streakline with α
Streamlines, Streaklines, and Pathlines
SOLO

112. 112
AERODYNAMICS
Streamlines, Streaklines, and Pathlines
SOLO

113. 113
AERODYNAMICSSOLO

114. 114
AERODYNAMICS
SOLO

115. 115
AERODYNAMICS
Streamlines, Streaklines, and Pathlines
SOLO
Return to Table of Content

116. 116
3-D Inviscid Incompressible Flow
Circulation
SOLO
Circulation Definition:
tV ∆

( ) tVV ∆∆+

S∆
Sn ∆1
V

×∇
t
r

∆
ttr ∆+∆

t
C
tt
C ∆+
∫ ⋅=Γ
C
rdV

:
Material Derivative of the Circulation
( )∫∫∫ ⋅+⋅=








⋅=
Γ
CCC
rd
tD
D
Vrd
tD
VD
rdV
tD
D
tD
D 


From the Figure we can see that:
( ) tVrtVVr ttt
∆+∆=∆∆++∆ ∆+

( ) Vdrd
tD
D
V
t
rr t
ttt

=→∆=
∆
∆−∆ →∆
∆+
0
( ) 0
2
2
=





=⋅=⋅ ∫∫∫ CCC
V
dVdVrd
tD
D
V

Therefore:
∫ ⋅=
Γ
C
rd
tD
VD
tD
D

integral of an exact differential on a closed curve.
C – a closed curve

117. 117
3-D Inviscid Incompressible FlowSOLO
tV ∆

( ) tVV ∆∆+

S∆
Sn ∆1
V

×∇
t
r

∆
ttr ∆+∆

t
C
tt
C ∆+
S
∫ ⋅=Γ
tC
rdV

:
Material Derivative of the Circulation (second derivation)
Subtract those equations:
tVrdSn t
∆×=∆

1
( )∫∆+
⋅∆+=Γ∆+Γ
ttC
rdVV

:
( ) ( )∫∫∫∫ ∆⋅×∇=⋅∆+−⋅=Γ∆−
∆+ S
TheoremsStoke
CC
SnVrdVVrdV
ttt
1
' 
S is the surface bounded by the curves Ct and C t+Δ t
( ) ( ) ( ) tVVrdtVrdVSnV
S
t
S
t
S
∆








×∇×⋅=∆×⋅×∇=∆⋅×∇=Γ∆− ∫∫∫∫∫∫

1
td
d
ttd
rd
t
V
ttD
D rdd
Γ
+
∂
Γ∂
=Γ∇⋅+
∂
Γ∂
=Γ∇⋅+
∂
Γ∂
=
Γ Γ∇⋅=Γ
Computation of:
∫ ⋅
∂
∂
=
∂
Γ∂
tC
rd
t
V
t

Computation of:
td
d Γ

118. 118
3-D Inviscid Incompressible FlowSOLO
tV ∆

( ) tVV ∆∆+

S∆
Sn ∆1
V

×∇
t
r

∆
tt
r ∆+
∆

t
C
tt
C ∆+
Material Derivative of the Circulation (second derivation)
( ) tVVrd
S
t
∆








×∇×⋅=Γ∆− ∫∫

When Δ t → 0 the surface S shrinks to the curve C=Ct and
the surface integral transforms to a curvilinear integral:
( ) ( ) ( )∫∫∫∫∫ ∇⋅⋅+





−=∇⋅⋅+





∇⋅−=×∇×⋅−=
Γ
C
t
CC
t
C
t
C
t
VVrd
V
dVVrd
V
rdVVrd
td
d 


0
22
22
Computation of: (continue)
td
d Γ
Finally we obtain:
( ) ∫∫∫ ⋅=∇⋅⋅+⋅
∂
∂
=
Γ
+
∂
Γ∂
=
Γ
tt CC
t
C
rd
tD
VD
VVrdrd
t
V
td
d
ttD
D




119. 119
3-D Inviscid Incompressible FlowSOLO
tV ∆

( ) tVV ∆∆+

S∆
Sn ∆1
V

×∇
t
r

∆
tt
r ∆+
∆

t
C
tt
C ∆+
Material Derivative of the Circulation
We obtained:
∫ ⋅=
Γ
tC
rd
tD
VD
tD
D

Use C.L.M.: hsT
p
VV
t
V
tD
VD
II
I
G
II
II
,,
,
,,
~
∇−∇+
⋅∇
+Ψ∇=








∇⋅+=
τ
∂
∂




( ) ( )

0
,
,,
,
,
~~
∫∫∫∫ −Ψ+⋅




 ⋅∇
+∇=⋅∇−Ψ∇+⋅




 ⋅∇
+∇=
Γ
tttt CC
I
I
C
I
C
I
I
I
hddrd
p
sTrdhrd
p
sT
tD
D ττ
to obtain:
∫ ⋅




 ⋅∇
+∇=
Γ
tC
I
I
I
rd
p
sT
tD
D τ~
,
,
or:
Kelvin’s Theorem
William Thomson
Lord Kelvin
(1824-1907)
In an inviscid , isentropic flow d s = 0 with conservative
body forces the circulation Γ around a closed fluid line
remains constant with respect to time.
0
~~ =τ
Ψ∇=G
1869
Return to Table of Content

120. 120
3-D Inviscid Incompressible FlowSOLO
Circulation Definition: ∫ ⋅=Γ
C
rdV

:
C – a closed curve
Biot-Savart Formula
1820
Jean-Baptiste Biot
1774 - 1862
VorticityV

×∇≡Ω
∫ −
Ω
=
Space
dV
sr
A 


π4
1
( )lddSn
sr
Ad




⋅
−
Ω
=
π4
1
The contribution of a length dl of the Vortex Filament
to isA

∫∫∫∫∫ ⋅Ω=⋅×∇=⋅=Γ
SS
Stokes
C
SdnSdnVrdV

:
If the Flow is Incompressible 0=⋅∇ u

so we can write , where is the Vector Potential. We are free to
choose so we choose it to satisfy .
AV

×∇=
A
 A

0=⋅∇ A

We obtain the Poisson Equation that defines the Vector Potential A

Ω−=∇

A2
Poisson Equation Solution( ) ∫ −
Ω
=
Space
dv
sr
rA 


π4
1
Félix Savart
1791 - 1841
Biot-Savart Formula

121. 121
3-D Inviscid Incompressible FlowSOLO
Circulation Definition: ∫ ⋅=Γ
C
rdV

:
C – a closed curve
Biot-Savart Formula (continue - 1)
1820
Jean-Baptiste Biot
1774 - 1862
VorticityV

×∇≡Ω
( )lddSn
sr
Ad




⋅
−
Ω
=
π4
1
We found
∫∫∫∫∫ ⋅Ω=⋅×∇=⋅=Γ
SS
Stokes
C
SdnSdnVrdV

:
also we have dlld
Ω
Ω
=


( ) ( ) ∫∫∫∫∫ ×
−
∇⋅Ω=⋅
−
Ω
×∇=×∇=
Γ
Ω
Ω
=
ld
sr
dSnlddSn
sr
AdrV r
S
dlld
v
rr









1
4
1
4
1
ππ
( ) ( )
∫ −
−×Γ
= 3
4 sr
srld
rV 


π Biot-Savart Formula
Félix Savart
1791 - 1841
Biot-Savart Formula

122. 122
3-D Inviscid Incompressible Flow
Circulation
SOLO
Circulation Definition: ∫ ⋅=Γ
C
rdV

:
C – a closed curve
Biot-Savart Formula (continue - 2)
1820
Jean-Baptiste Biot
1774 - 1862
( ) ( )
∫ −
−×Γ
= 3
4 sr
srld
rV 


π
Biot-Savart Formula
General 3D Vortex
Félix Savart
1791 - 1841

123. 123
3-D Inviscid Incompressible FlowSOLO
Circulation Definition: ∫ ⋅=Γ
C
rdV

:
C – a closed curve
Biot-Savart Formula (continue - 3)
1820
Jean-Baptiste Biot
1774 - 1862
Félix Savart
1791 - 1841
( ) ( )
∫ −
−×Γ
= 3
4 sr
srld
rV 


π
Biot-Savart Formula
General 3D Vortex
For a 2 D Vortex:
( ) θ
θ
θθ
θ
d
hsr
dl
sr
srld sinˆˆsin
23
=
−
=
−
−×


θ
θ
θ d
h
dlhl 2
sin
cot =⇒=−
θsin/hsr =−

θ
π
θθθ
π
π
ˆ
2
sinˆ
4 0
h
d
h
V
Γ
=
Γ
= ∫
 Biot-Savart Formula
General 2D Vortex
Biot-Savart Formula

124. 124
3-D Inviscid Incompressible FlowSOLO
Circulation Definition: ∫ ⋅=Γ
C
rdV

:
C – a closed curve
Biot-Savart Formula (continue - 4)
1820
Jean-Baptiste Biot
1774 - 1862( ) ( )
∫ −
−×Γ
= 3
4 sr
srld
rV 


π
Biot-Savart Formula
General 3D Vortex
Félix Savart
1791 - 1841
Lifting-Line Theory
Biot-Savart Formula
Return to Table of Content

125. 125
3-D Inviscid Incompressible Flow
Helmholtz Vortex Theorems
SOLO
Helmholtz : “Uber the Integrale der hydrodynamischen Gleichungen, welche
Den Wirbelbewegungen entsprechen”, (“On the Integrals of the Hydrodynamical
Equations Corresponding to Vortex Motion”), in Journal fur die
reine und angewandte, vol. 55, pp. 25-55. , 1858
He introduced the potential of velocity φ.
Hermann Ludwig Ferdinand
von Helmholtz
1821 - 1894
Theorem 1: The circulation around a given vortex line (i.e.,
the strength of the vortex filament) is constant along its length.
Theorem 2: A vortex filament cannot end in a fluid. It must
form a closed path, end at a boundary, or go to infinity.
Theorem 3: No fluid particle can have rotation, if it did not originally rotate.
Or, equivalently, in the absence of rotational external forces, a fluid that is
initially irrotational remains irrotational. In general we can conclude that the
vortex are preserved as time passes. They can disappear only through the action
of viscosity (or some other dissipative mechanism).
1858
Return to Table of Content

126. 126
2-D Inviscid Incompressible Flow
In 2-D the velocity vector
SOLO
Stream Function ψ, Velocity Potential φ in 2-D Incompressible Irrotational Flow
x
y V

u
v
ru
θv
r
θ
θθ 1111 vruyvxuV r
+=+=

θ
θ
∂
∂
++
∂
∂
=
∂
∂
+
∂
∂
=⋅∇
v
r
u
r
u
y
v
x
u
V rr

z
u
r
v
z
u
r
z
v
z
y
u
x
v
y
z
u
x
z
v
V rr
111111 





∂
∂
−
∂
∂
+
∂
∂
+
∂
∂
−=





∂
∂
−
∂
∂
+
∂
∂
+
∂
∂
−=×∇
θ
θ θθ

0
111
0
111
rr vu
zr
zr
vu
zyx
zyx
V
∂
∂
∂
∂
∂
∂
=
∂
∂
∂
∂
∂
∂
=×∇
θ
θ













−
=





v
u
v
ur
θθ
θθ
θ cossin
sincos ( ) θ
θ
i
r
eviuviu +=+
( ) θ
θ
i
r
eviuviu −
+=+

127. 127
2-D Inviscid Incompressible Flow
In 2-D the velocity vector
SOLO
Stream Function ψ, Velocity Potential φ in 2-D Incompressible Irrotational Flow
x
y V

u
v
ru
θv
r
θ
θθ 1111 vruyvxuV r
+=+=













−
=





v
u
v
ur
θθ
θθ
θ cossin
sincos ( ) θ
θ
i
r
eviuviu +=+
( ) θ
θ
i
r
eviuviu −
+=+
Continuity: 00 =⋅∇→=⋅∇+ uu
tD
D 
ρ
ρ
( )







∂
∂
−=
∂
∂
=×





∂
∂
+
∂
∂
∂
∂
−=
∂
∂
=×





∂
∂
+
∂
∂
=×∇=×∇=
r
v
r
uz
r
r
r
x
v
y
uzy
y
x
x
zzu
r
ψ
θ
ψ
θ
θ
ψψ
ψψψψ
ψψ
θ
1
11
1
1
111
11 22

Incompressible: 0=
tD
D ρ
Irrotational:







∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
=
=∇=
θ
φφ
φφ
φ
θ
r
v
r
u
y
v
x
u
u
r
1
2

0=×∇ u

rr
v
rr
u
xy
v
yx
u
r
∂
∂
−=
∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
−=
∂
∂
=
∂
∂
=
∂
∂
=
ψ
θ
φ
θ
ψφ
ψφψφ
θ
11

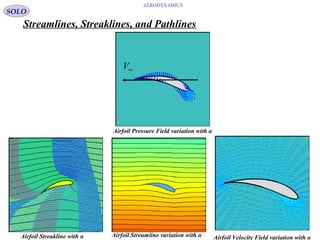
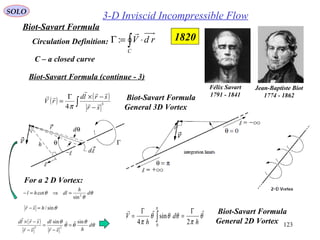
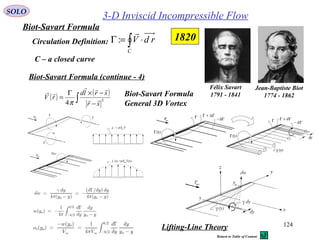
128. 128
2-D Inviscid Incompressible Flow
In 2-D the velocity vector
SOLO
Stream Function ψ, Velocity Potential φ in 2-D Incompressible Irrotational Flow
x
y V

u
v
ru
θv
r
θ
θθ 1111 vruyvxuV r
+=+=













−
=





v
u
v
ur
θθ
θθ
θ cossin
sincos ( ) θ
θ
i
r
eviuviu +=+
( ) θ
θ
i
r
eviuviu −
+=+
00 222
=∇⋅∇→∇=+=⋅∇ φφuu

2-D Incompressible:
2-D Irrotational:
( )
( ) ( ) ( )ψψψ
ψψ
222
0
222
222
1110
110
∇⋅∇−∇∇⋅=×∇×∇=
→×∇=×∇=+=×∇
zzz
zzuu


 0
2
2
2
2
=∇=∇ ψφ
Complex Potential in 2-D Incompressible-Irrotational Flow:
( ) ( ) ( )
yixz
yxiyxzw
+=
+= ,,: ψφ
( ) =
zd
zwd
x
i
x ∂
∂
+
∂
∂ ψφ
yy
i
∂
∂
+
∂
∂
−
ψφ0=x
0=y
( )[ ] ( ) θ
θ
θ
θ
i
r
i
r
eviueviuVviu −∗∗
−=+==−
zd
wd
viu =− θ
θ
i
r e
zd
wd
viu =−
xyyx ∂
∂
−=
∂
∂
∂
∂
=
∂
∂ ψφψφ
Cauchy-Riemann Equations
We found:

129. 129
2-D Inviscid Incompressible Flow
Examples:
SOLO
Stream Function ψ, Velocity Potential φ in 2-D Incompressible Irrotational Flow
αα sincos 00
UiUV +=Uniform Stream:
xy
Uv
yx
Uu
∂
∂
−=
∂
∂
==
∂
∂
=
∂
∂
==
ψφ
α
ψφ
α
sin
cos
0
0
( ) ( )
( ) ( ) yUxU
yUxU
ααψ
ααφ
cossin
sincos
00
00
+−=
+=
( ) ( )
zU
zUzUiw
∗
=
−=+=
0
00 sincos ααψφ
0
U
α

130. 130
2-D Inviscid Incompressible Flow
Examples:
SOLO
Stream Function ψ, Velocity Potential φ in 2-D Incompressible Irrotational Flow







∂
∂
−=
∂
∂
==
∂
∂
=
∂
∂
==
rr
v
rrr
m
ur
ψ
θ
φ
θ
ψφ
π
θ
1
0:
1
2
:
( )













==
+==
−
x
ymm
yx
m
r
m
1
22
tan
22
ln
2
ln
2
π
θ
π
ψ
ππ
φ
( ) ( ) z
m
re
m
ir
m
iw i
ln
2
ln
2
ln
2 ππ
θ
π
ψφ θ
==+=+=
Definition:
Source , Sink :( )0>m ( )0<m
Sink 0<m
Source 0>m
The equation of a streamline is: const
m
== θ
π
ψ
2

131. 131
2-D Inviscid Incompressible Flow
Examples:
SOLO
Stream Function ψ, Velocity Potential φ in 2-D Incompressible Irotational Flow
( ) ( ) ( )
r
K
vvr
r
zuvr
r
Vu
r
rr =→=
∂
∂
→=





∂
∂
−
∂
∂
=×∇→=
≠
θθθ
θ
0010:
0
2

( )






+
Γ
=
Γ
=





Γ
−=
Γ
−= −
22
1
ln
2
ln
2
tan
22
yxr
x
y
ππ
ψ
π
θ
π
φ
( ) ( ) z
i
re
i
riiw i
ln
2
ln
2
ln
2 ππ
θ
π
ψφ θ Γ
=
Γ
=+−
Γ
=+=
Definition:
Infinite Line Vortex :







∂
∂
−=
∂
∂
−=
Γ
−=
∂
∂
=
∂
∂
−==
rrr
v
rr
ur
ψ
θ
φ
π
θ
ψφ
θ
1
2
:
1
0:
( ) Γ−=
Γ−
=+⋅




 Γ−
=⋅ ∫∫∫ θ
π
θθθ
π
ddrrdr
r
drV
2
111
2
Circulation
streamlines:
( )
Λ
=+
→+
Γ
=
/222
22
ln
2
ψπ
π
ψ
eyx
yx
Irotational

132. 132
2-D Inviscid Incompressible Flow
Examples:
SOLO
Stream Function ψ, Velocity Potential φ in 2-D Incompressible Irrotational Flow
Definition: Let have a source and a sink of equal strength m = μ/ε situated at x = -ε
and x = ε such that
Doublet at the Origin with Axis Along x Axis :
m+ m−
ε+ε−
y
x
.lim0
constm ==→
µεε
( ) ( ) ( )






−
+
=





−
+
=
−−+=
z
zm
z
zm
z
m
z
m
zw
/1
/1
ln
2
ln
2
ln
2
ln
2
ε
ε
πε
ε
π
ε
π
ε
π
.lim0
constm ==→
µεεwhen
( )
zz
m
z
O
z
m
z
O
zz
m
z
zm
zw
m
π
µε
π
εε
π
εεε
πε
ε
π
µε =
=≈













++≈














++





+≈





−
+
=
2
2
21ln
2
11ln
2/1
/1
ln
2
2
2
2
2

133. 133
2-D Inviscid Incompressible Flow
Examples:
SOLO
Stream Function ψ, Velocity Potential φ in 2-D Incompressible Irrotational Flow
( ) ( )θθ
πππ
sincos
2
1
2
ln
2
: i
r
m
z
m
z
m
zd
d
zd
Wd
zw Source
Doublet −==





==







+
==
+
==
=
=
22
2/
22
2/
sin
cos
yx
y
r
yx
x
r
m
m
π
µ
θ
π
µ
ψ
π
µ
θ
π
µ
φ
µ
µ
Definition:
Doublet at the Origin with Axis Along x Axis (continue):
2
1
2
1
2 z
m
z
m
zd
d
zd
wd
viuV
ππ
−=





==−=∗
The equation of a streamline is: .
22
const
yx
y
=
+
=
π
µ
ψ
22
2
22 





=





++
ψ
µ
ψ
µ
yx

134. 134
SOLO
2-D Inviscid Incompressible Flow
Stream Functions (φ), Potential Functions (ψ) for Elementary Flows
Flow W (z=reiθ
)=φ+i ψ φ ψ
Uniform Flow θcosrU∞ θsinrU∞
( )yixUzU += ∞∞
Source ( )θ
ππ
i
re
k
z
k
ln
2
ln
2
= r
k
ln
2π
θ
π2
k
Doublet
θi
er
B
z
B
= θcos
r
B
θsin
r
B
−
Vortex
(with clockwise
Circulation)
( )θ
ππ
i
re
i
z
i
ln
2
ln
2
Γ
=
Γ
θ
π2
Γ−
rln
2π
Γ
90◦
Corner Flow ( )22
22
yix
A
z
A
+= yxA( )22
2
yx
A
−
Return to Table of Content

135. 135
SOLO
2-D Inviscid Incompressible Flow
Paul Richard Heinrich Blasius
(1883 – 1970)
Blasius was a PhD Student of Prandtl at Götingen University
x
y
xδ
yδ
β
sd
M














−=






=−
∫
∫
C
C
zd
zd
wd
zM
zd
zd
wdi
iYX
2
2
2
2
ρ
ρ
Re
where
-w (z) – Complex Potential of a Two-Dimensional Inviscid Flow
-X, Y – Force Components in x and y directions of the Force per Unit Span on
the Body
-M – the anti-clockwise Moment per Unit Span about the point z=0
-ρ – Air Density
-C – Two Dimensional Body Boundary Curve
1911Blasius Theorem

136. 136
SOLO
2-D Inviscid Incompressible Flow
Paul Richard Heinrich Blasius
(1883 – 1970)
Blasius was a PhD Student of Prandtl at Götingen University














−=






=−
∫
∫
C
C
zd
zd
wd
zM
zd
zd
wdi
iYX
2
2
2
2
ρ
ρ
Re
1911Blasius Theorem
Proof of Blasius Theorem
Consider the Small Element δs on the Boundary C
sysx δβδδβδ cos,sin =−=
xpspY
ypspX
δδβδ
δδβδ
⋅=⋅−=
⋅−=⋅−=
sin
cos
then
p = Normal Pressure to δs
The Total Force on the Body is given by
( ) ( )∫∫ −⋅−=+⋅−=−
CC
ydixdpixdiydpYiX
Use Bernoulli’s Theorem .
2
1 2
constUp =+ ∞ρ
U∞ = Air Velocity far from Body
x
y
xδ
yδ
β
sd
M
X
Y

137. 137
SOLO
2-D Inviscid Incompressible Flow
Paul Richard Heinrich Blasius
(1883 – 1970)
Blasius was a PhD Student of Prandtl at Götingen University














−=






=−
∫
∫
C
C
zd
zd
wd
zM
zd
zd
wdi
iYX
2
2
2
2
ρ
ρ
Re
1911Blasius Theorem
Proof of Blasius Theorem (continue – 1)
( )∫ −⋅





−−=− ∞
C
ydixdUconstiYiX
2
2
1
ρ
but ( ) 00 =−⋅⇒== ∫∫∫ CCC
ydixdconstydxd
( ) ( )( ) ( )( ) ( )
( )( )
( ) ( ) ( ) ( ) yduivuxduivvdyixdviu
dyuixdvdyixdvu
dyvuidyixdvudyixdvudyixdU
+−+++−=
−++−=
+−++=−+=−∞
22
22
2
2
2222
2222222
viuU +=∞
and
x
y
xδ
yδ
β
sd
M
X
Y

138. 138
SOLO
2-D Inviscid Incompressible Flow
Paul Richard Heinrich Blasius
(1883 – 1970)
Blasius was a PhD Student of Prandtl at Götingen University














−=






=−
∫
∫
C
C
zd
zd
wd
zM
zd
zd
wdi
iYX
2
2
2
2
ρ
ρ
Re
1911Blasius Theorem
Proof of Blasius Theorem (continue – 2)
( ) ∫∫ ⋅





=−⋅=− ∞
CC
zd
zd
wdi
ydixdU
i
YiX
2
2
22
ρρ
( ) ( ) ( ) zd
zd
wd
dyixdviudyixdU
2
22






=+−=−∞
( ) ( ) 00 =−⇒+×+=×= ∞ xdvyduviuydixdUsd

Since the Flow around C is on a Streamline defined by
therefore ( ) ( ) yduivuxduivv +=+ 22
( ) ( ) ( )
yixz
yxiyxzw
+=
+= ,,: ψφ
and
xy
v
yx
u
∂
∂
−=
∂
∂
=
∂
∂
=
∂
∂
=
ψφψφ
,where
Completes the Proof for the Force Equation
viu
zd
wd
−=
x
y
xδ
yδ
β
sd
M
X
Y

139. 139
SOLO
2-D Inviscid Incompressible Flow
Paul Richard Heinrich Blasius
(1883 – 1970)
Blasius was a PhD Student of Prandtl at Götingen University














−=






=−
∫
∫
C
C
zd
zd
wd
zM
zd
zd
wdi
iYX
2
2
2
2
ρ
ρ
Re
1911Blasius Theorem
Proof of Blasius Theorem (continue – 3)
( )( ) ( ) ( )( )ydxixdyiydyxdxvuivudyixdviuyixzd
zd
wd
z ++−−−=+−+=





2222
2
The Moment around the point z=0 is defined by
( ) ( )∫∫ +⋅−=+⋅= ∞
CC
ydyxdxUydyxdxpM
2
2
ρ
since 2
2
∞−= Uconstp
Bernoulli ρ
and ( ) 0=+⋅∫C
ydyxdxconst
hence
( )( ) ( )xdyydxvuydyxdxvuzd
zd
wd
z ++−−=














222
2
Re
x
y
xδ
yδ
β
sd
M
X
Y

140. 140
SOLO
2-D Inviscid Incompressible Flow
Paul Richard Heinrich Blasius
(1883 – 1970)
Blasius was a PhD Student of Prandtl at Götingen University














−=






=−
∫
∫
C
C
zd
zd
wd
zM
zd
zd
wdi
iYX
2
2
2
2
ρ
ρ
Re
1911Blasius Theorem
Proof of Blasius Theorem (continue – 4)
( ) ( ) ( )














−=+⋅+−=+⋅= ∫∫∫ CCC
zd
zd
wd
zydyxdxvuydyxdxpM
2
22
22
ρρ
Re
hence
( )( ) ( )xdyydxvuydyxdxvuzd
zd
wd
z ++−−=














222
2
Re
Since the Flow around C is on a Streamline we found that u dy = v dx
( ) ( ) ( ) ydyuxdxvxdvyuyduxvxdyydxvu 22
22222 +=+=+
( ) ( )ydyxdxvuzd
zd
wd
z ++=













 22
2
2Re
Completes the Proof for the Moment Equation
x
y
xδ
yδ
β
sd
M
X
Y

141. 141
SOLO
2-D Inviscid Incompressible Flow
Blasius Theorem Example
Circular Cylinder with Circulation
Let apply Blasius Theorem
Assume a Cylinder of Radius a in a Flow of Velocity U∞ at an Angle of Attack α
and Circulation Γ.
The Flow is simulated by:
-A Uniform Stream of Velocity U∞
-A Doublet of Strength U∞ a2
.
-A Vortex of Strength Γ at the origin.
Since the Closed Loop Integral is nonzero only for 1/z component, we have
viu
z
i
z
eaU
eU
zd
wd i
i
−=
Γ
−−=
+
∞−
∞
π
α
α
22
2
∫∫ ⋅




 Γ
−−=⋅





=−
+
∞−
∞
C
i
i
C
zd
z
i
z
eaU
eU
i
zd
zd
wdi
YiX
2
2
22
222 π
ρρ
α
α
α
αα
ρ
π
ρ
π
ρ i
i
C
i
eUi
z
eU
Residuezd
z
eUii
YiX −
∞
−
∞
−
∞
Γ=




 Γ
=⋅




 Γ
−=− ∫ 22
02 =





==⋅∫ zenclosesCif
z
A
ResidueAizd
z
A
C
πwhere we used:
α
α
X
Y−L
∞U
x
y
( ) ( )α
α
α
π
i
i
i
ez
i
ez
aU
ezUzw −
−
∞−
∞
Γ
−+= ln
2
2

142. 142
SOLO
2-D Inviscid Incompressible Flow
Blasius Theorem Example
Circular Cylinder with Circulation (continue – 1)













 Γ
−−−=














−= ∫∫
+
∞−
∞
C
i
i
C
zd
z
i
z
eaU
eUzzd
zd
wd
zM
2
2
22
222 π
ρρ α
α
ReRe
Since the Closed Loop Integral is nonzero only for 1/z component, we have





=≠
==





=
=⋅∫
0'10
012
zenclosendoesCornif
zenclosesCandnif
z
A
ResidueAi
zd
z
A
C
n
π
we used:
0
4
22
24
2
2 2
2
22
2
222
=











 Γ
−−=















 Γ
−−= ∞
∞
∫ π
π
ρ
π
ρ
aUizd
zz
aU
M
C
ReRe
α
ρ i
eUiYiX −
∞Γ=−
( )



Γ=
=
⇒Γ=−=+
∞
∞
−
UL
D
UieYiXiLD i
ρ
ρα 0
:
α
α
X
Y−L
∞U
x
y
Zero Moment around the Origin.

143. 143
SOLO
2-D Inviscid Incompressible Flow
Blasius Theorem Example
Circular Cylinder with Circulation (continue – 2)
On the Cylinder z = a e iθ
We found: viu
z
i
z
eaU
eU
zd
wd i
i
−=
Γ
−−=
+
∞−
∞
π
α
α
22
2
( )
( ) 




 Γ
−−=
=
Γ
−−==−=−
∞
−+
∞
−
∞
a
Ui
a
i
eeUeeUe
zd
Wd
eviuviv iiiiii
r
π
αθ
π
θαθαθθ
θ
2
sin2
2
Stagnation Points are the Points on the Cylinder for which vθ = 0:
( ) 0
2
sin2 =
Γ
−−=− ∞
a
Uv
π
αθθ





 Γ
+=
∞
−
Ua
stagnation
π
αθ
4
sin 1

144. 144
The Flow Pattern Around a Spinning Cylinder
with Different Circulations Γ Strengths
2-D Inviscid Incompressible FlowSOLO

145. 145
SOLO
2-D Inviscid Incompressible Flow
Blasius Theorem Example
Circular Cylinder with Circulation (continue – 3)
The Pressure Coefficient on the Cylinder Surface is given by:
( )
2
2
2
22
2
2
sin2
11
2
1 ∞
∞
∞
∞
∞





 Γ
−−
−=
+
−=
−
=
U
a
U
U
vv
U
pp
C rSurface
Surfacep
π
αθ
ρ
θ
Using Bernoulli’s Law:
22
2
1
2
1
∞∞ +=+ UpUp SurfaceSurface ρρ
( ) ( ) 




 Γ
−+




 Γ
−−−=
∞∞ UaUa
C
Surfacep
π
αθ
π
αθ
4
sin8
4
4sin41
2
2

146. 146
2-D Inviscid Incompressible FlowSOLO

147. 147
SOLO
Stream Lines
Flow Around a Cylinder
Streak Lines (α = 0º)
Preasure Field
Streak Lines (α = 5º)
Streak Lines (α = 10º) Forces in the Body
http://www.diam.unige.it/~irro/cilindro_e.html
2-D Inviscid Incompressible Flow

148. 148
SOLO
Velocity Field
http://www.diam.unige.it/~irro/cilindro_e.html
University of Genua, Faculty of Engineering,
2-D Inviscid Incompressible Flow
Return to Table of Content

149. 149
SOLO
2-D Inviscid Incompressible Flow
C
'C
''C '''C
Corollary to Blasius Theorem














−=














−=






=





=−
∫∫
∫∫
'
22
'
22
22
22
CC
CC
zd
zd
wd
zzd
zd
wd
zM
zd
zd
wdi
zd
zd
wdi
iYX
ρρ
ρρ
ReRe
C – Two Dimensional Curve defining Body Boundary
C’ – Any Other Two Dimensional Curve inclosing C
such that No Singularity exist between C and C’
Proof of Corollary to Blasius Theorem
Add two Close Paths C” and C”’ , connecting C and C’, in opposite direction, s.t.
∫∫ −=
''''' CC
then, since there are No Singularities between C and C’, according to Cauchy:
0
'
0
'''''
=−++ ∫∫∫∫ CCCC

q.e.d.
∫∫ =
'CC
therefore

150. 150
SOLO
2-D Inviscid Incompressible Flow

151. 151
2-D Inviscid Incompressible Flow
AERODYNAMICS
Subsonic Incompressible Flow (ρ∞ = const.) about Wings of Infinite Span (AR = ∞)
SOLO
Return to Table of Content

152. 152
Kutta Condition
We want to obtain an analogy between a Flow around an Airfoil and that around a
Spinning Cylinder. For the Spinning Cylinder we have seen that when a Vortex is
Superimposed with a Doublet on an Uniform Flow, a Lifting Flow is generated.
The Doublet and Uniform Flow don’t generate Lift. The generation of Lift is always
associated with Circulation.
Suppose that is possible to use Vortices to generate Circulation, and therefore
Lift, for the Flow around an Airfoil.
• Figure (a) shows the pure non-circulatory Flow around an Airfoil at an Angle of
Attack. We can see the Fore SF and Aft SA Stagnation Points.
•Figure (b) shows a Flow with a Small Circulation added. The Aft Stagnation Point
Remains on the Upper Surface.
•Figure (c) shows a Flow with Higher Circulation, so that the Aft Stagnation Point
moves to Lower Surface. The Flow has to pass around the Trailing Edge. For an
Inviscid Flow this implies an Infinite Speed at the Trailing Edge.
•Figure (d) shows the only possible position for the Aft Stagnation Point, on the
Trailing Edge. This is the Kutta Condition, introduced by Wilhelm Kutta in 1902,
“Lift Forces in Flowing Fluids” (German), Ill. Aeronaut. Mitt. 6, 133.
Martin Wilhelm
Kutta
(1867 – 1944)
2-D Inviscid Incompressible Flow
1902
SOLO
Definition: A Stagnation Point is a point in a flow field where the local velocity
of the fluid is zero

153. 153
Effect of Circulation on the Flow around an Airfoil at an Angle of Attack
2-D Inviscid Incompressible FlowSOLO
Definition: A Stagnation Point is a point in a flow field where the local velocity
of the fluid is zero
SF – Forward Stagnation Point
SA – Aft Stagnation Point
Kutta Condition:
SA on the Trailing Edge
Return to Table of Content

154. 154
Martin Wilhelm Kutta
(1867 – 1944)
Nikolay Yegorovich Joukovsky
(1847-1921
Kutta-Joukovsky Theorem
The Kutta–Joukowsky Theorem is a Fundamental Theorem of
Aerodynamics. The theorem relates the Lift generated by a right
cylinder to the speed of the cylinder through the fluid, the density
of the fluid, and the Circulation. The Circulation is defined as the
line integral, around a closed loop enclosing the cylinder or
airfoil, of the component of the velocity of the fluid tangent to the
loop. The magnitude and direction of the fluid velocity change
along the path.
The force per unit length acting on a right cylinder of any
cross section whatsoever is equal to ρ∞V∞Γ, and is
perpendicular to the direction of V∞.
Kutta–Joukowsky Theorem:
2-D Inviscid Incompressible Flow
19061902
Γ= ∞∞UL ρKutta–Joukowsky Theorem:
LCUL
2
2
1
∞∞= ρLift:
Kutta in 1902 and Joukowsky in 1906, independently, arrived to this result.
Circulation ∫∫ =⋅=Γ θcos: ldVldV

SOLO

155. 155
SOLO
2-D Inviscid Incompressible Flow
General Proof of Kutta-Joukovsky Theorem
Using the Corollary to Blasius Theorem
Suppose that we wish to determine the
Aerodynamic Force on a Body of Any Shape.
Use Corollary to Blasius Theorem, integrating
Round a Circle Contour with a Large Radius and
Center on the Body
( ) z
i
z
aU
zUzw ln
2
2
π
Γ
−+= ∞
∞
The proof is identical to development in the Example of
Flow around a Two Dimensional Cylinder using
According to Corollary to Blasius Theorem we use C’ instead of C for Integration
z
i
z
aU
U
zd
wd 1
22
2
π
Γ
−−= ∞
∞
LiftiDragUi
Ui
i
i
z
Ui
Residue
i
zd
z
Uii
zd
z
i
z
aU
U
i
zd
zd
wdi
zd
zd
wdi
iYX
CCCC
+=Γ=




 Γ
−=




 Γ
−=





 Γ
−=




 Γ
−−=





=





=−
∞
∞∞
∞∞
∞ ∫∫∫∫
ρ
π
π
ρ
π
ρ
π
ρ
π
ρρρ
2
2
1
2
1
2
1
2222 ''
2
2
2
'
22
Therefore 0& =Γ== ∞ DragULLift ρ
q.e.d.
02 =





==⋅∫ zenclosesCif
z
A
ResidueAizd
z
A
C
πwhere we used:
C
'C
∞U
L
D

156. 156
SOLO
2-D Inviscid Incompressible Flow
D’Alembert Paradox
The fact that the Inviscid Flow Theories give Drag = 0 is called D’Alembert Paradox.
In 1768 d’Alembert enunciated his famous paradox in the following words:
“Thus I do not see, I admit, how one can satisfactorily explain by
theory the resistance of fluids. On the contrary, it seems to me that the
theory, developed in all possible rigor, gives, at least in several cases,
a strictly vanishing resistance; a singular paradox which I leave to
future geometers for elucidation.”
Jean-Baptiste le Rond
d'Alembert
(1717 – 1783)
The resistance (Drag) experienced by a Real Airfoil is do to
a combination of Skin-Friction and Pressure Distribution
Distortions due to displacements effects of its Boundary
Layers, which are not considered in the Inviscid Flow
Theories.

157. 157
The Kutta-Joukowsky Theory can be used to design Wings of Infinite Span that flow
at Subsonic Speeds (Incompressible Flows).
The design methods for such wings are called methods of “Profile Theory”.
AERODYNAMICS
Subsonic Incompressible Flow (ρ∞ = const.) about Wings of Infinite Span (AR = ∞)
Profile (of Airfoil) Theory can be treated in two different ways:
1.Conformal Mapping
This Method is limited to 2 – dimensional problems.
The Flow about a given body is obtained by using Conformal Mapping to
transform it into a known Flow about another body (usually Circular Cylinder)
2.Method of Singularities
The body in the Flow Field is substitute by Sources, Sinks, and Vortices, the so
called Singularities.
For practical purposes the Method of Singularities is much simpler than Conformal
Mapping. But, the Method of Singularities produces, in general, only Approximate
Solution, whereas Conformal Mapping leads to Exact Solutions, although these
often require considerable effort.
SOLO
Return to Table of Content

158. 158
Joukovsky Airfoils
Joukovsky transform, named after Nikolai Joukovsky is a
conformal map historically used to understand some
principles of airfoil design.
Nikolay Yegorovich Joukovsky
(1847-1921
Profile Theory Using Conformal Mapping
It is applied on a Circle of Radius R
and Center at cx, cy. The radius to
the Point (a,0) make an angle β to x
axis. Velocity U∞ makes an angle α
with x axis.
β
xc
yc
∞U
R
α
x
y
( )0,a
The transform is
z
a
z
2
+=ζ
( ) ββ sincosˆ RiRacicc yx +−=+=
For α=0 we have
( ) ( ) ( )cz
i
cz
R
czUzw ˆln
2ˆ
ˆ
2
−
Γ
+





−
+−= ∞
π
For any α we have
( ) ( ) ( )cez
i
cez
R
cezUzw i
i
i
ˆln
2ˆ
ˆ
2
−
Γ
+





−
+−= −
−
−
∞
α
α
α
π
AERODYNAMICSSOLO

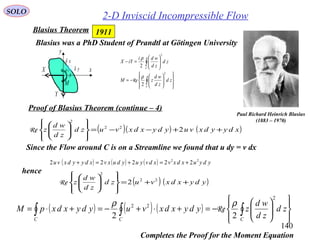
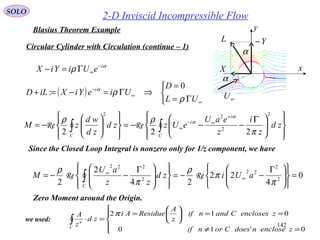
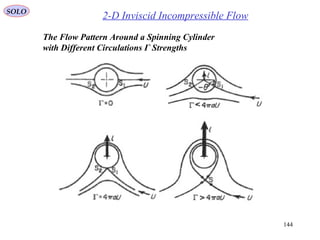
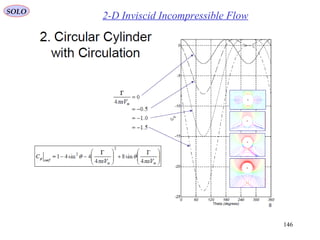
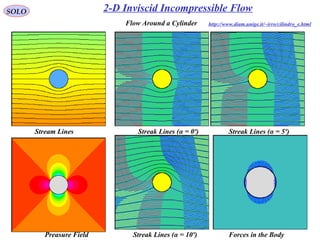
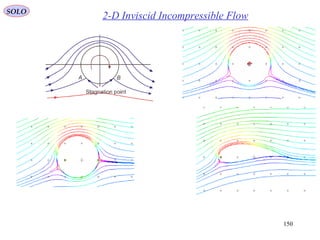
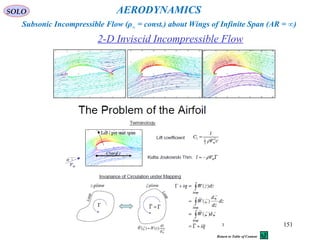
159. 159
Kutta-Joukovsky
Nikolay Yegorovich Joukovsky
(1847-1921
( ) ( ) ( )cez
i
cez
R
cezUzw i
i
i
ˆln
2ˆ
ˆ
2
−
Γ
+





−
+−= −
−
−
∞
α
α
α
π
( )
viu
cez
i
cez
R
Ue
zd
wd
ii
i
−=








−
Γ
+








−
−= −−∞
−
ˆ
1
2ˆ
1 2
2
αα
α
π
we have
Kutta Condition: The Flow Leaves Smoothly from the Trailing Edge.
This is an Empirical Observation that results from the tendency of
Viscous Boundary Layer to Separate at Trailing Edge.
Martin Wilhelm Kutta
(1867 – 1944)
( )
( )
( ) yx
i
ii
i
az
az
caBcaA
BiA
i
BiA
R
Ue
cea
i
cea
R
Ue
zd
wd
ivu
+=−=








−
Γ
+





−
−=








−
Γ
+








−
−===−
∞
−
−−∞
−
=
=
αα
π
π
α
αα
α
sin:,cos:
1
2
1
ˆ
1
2ˆ
10
2
2
2
2
( ) ( )[ ] ( ) ( )
( )














+





 Γ
++−+




 Γ
+−−−+
=
∞∞
−
222
22222222222
2
2
2
BA
BAAURBAiBABBARBAU
e i ππα
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO
Return to Table of Content

160. 160
we have
( ) ( )[ ] ( ) ( )
( )














+





 Γ
++−+




 Γ
+−−−+
==
∞∞
−
=
222
22222222222
2
2
2
0
BA
BAAURBAiBABBARBAU
e
zd
wd i
az
ππα
( ) βααβαα sinsinsin:,coscoscos: RacaBRaacaA yx +=+=−−=−=
( ) ( )
( ) ( )[ ] 222
2222
coscos2cos12
sinsincoscos
RRaRa
RaaRaBA
≈−−++−=
++−+=+
ββαα
βαβα
( ) π2
20 222 Γ
++−= ∞ BAAURBA ( )βαπππ sinsin444 22
2
RaUUBUB
BA
R
+=≈
+
=Γ ∞∞∞
( ) ( )[ ] ( ) ( ) ( )[ ]
( ) ( )[ ] ( )( ) 0
2
2
22222222222
2222222222222222
≈−++=+−+=
−−−+=
Γ
+−−−+
∞∞
∞∞∞
RBABAUBARBAU
URBBARBAUBABBARBAU
π
Let check
For this value of Γ, we have
This value of Γ satisfies the Kutta Condition
0=
=az
zd
wd
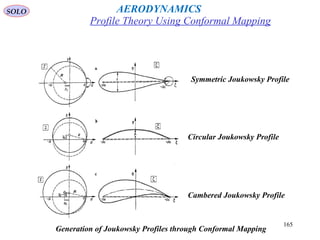
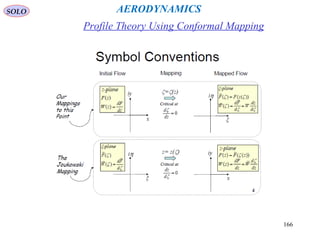
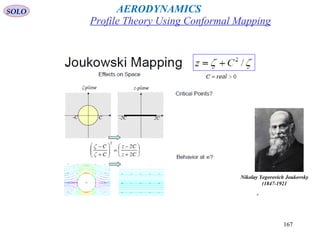
Joukovsky Airfoils
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

161. 161
Joukovsky Airfoils Design
1. Move the Circle to ĉ and choose Radius R so that the Circle
passes through z = a.
Nikolay Yegorovich Joukovsky
(1847-1921
β
xc
yc
∞U
R
α
x
y
( )0,a
for Center at z = 0.( ) z
i
z
R
zUzW ln
2
2
π
Γ
+





+= ∞
2. Change z-ĉ → z
( ) ( )cz
i
cz
R
czUzW ˆln
2ˆ
ˆ
2
−
Γ
+





−
+−= ∞
π
3. Change z → z e-iα
( ) ( )cez
i
cez
R
cezUzW i
i
i
ˆln
2ˆ
ˆ
2
−
Γ
+





−
+−= −
−
−
∞
α
α
α
π
4. Compute Γ from Kutta Condition
aza
zd
Wd
d
Wd
==
==
2
0
ς
ς ( )βαπ +=Γ ∞
<<
sin4
ˆ
RU
ac
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

162. 162
Joukovsky Airfoils Design (continue – 1)
5. Use the Transformation and compute
z
a
z
2
+=ζ
22
/1
/
/
za
zdWd
zd
d
zd
Wd
d
Wd
−
==
ς
ς
6. To Compute Lift use either:
( )βαρπρ +=Γ= ∞∞ sin4
2
RUUL6.1 Kutta-Joukovsky
6.2 Blasius( ) 













=−=− ∫ ς
ς
ραα
d
d
Wd
ieFiFeLi i
yx
i
2
2
''
6.3 Bernoulli
( )
2
2
/
1
2/ ∞∞
∞
−=
−
=
U
zdWd
U
pp
Cp
ρ








−=








−= ∫∫∫∫ −−
∞
−−
a
a
p
a
a
p
a
a
Upp
a
a
Low xdCxdC
U
xdpxdpL UL
2
2
2
2
22
2
2
2
''
cos
2/
''
cos
1
α
ρ
α
( ) ( )βαπβαπ
ρ
+≈+==
≈
≈
∞
sin2sin8
2/ 42
cR
ac
L
c
R
Uc
L
C
'yF
'xF 'xF
∞U
'x
L
α
plane−ς
'y
α
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

163. 163
Joukovsky Airfoils Design (continue – 2)
7. To compute Pitching Moment about Origin use either:
7.2 Blasius














= ∫ ςς
ς
ρ
d
d
Wd
iM p
2
20
Re
7.1 Bernoulli








+−=
+−=
∫∫
∫∫
−−
∞
−−
a
a
p
a
a
p
a
a
Upp
a
a
Low
SpanUnitper
p
xdxCxdxC
U
xdxpxdxpM
UL
2
2
2
2
2
2
2
2
2
''''
2
''''0
ρ
'yF
'xF 'xF
∞U
'x
L
α
plane−ς
'y
α
0pM
απ
ρ
2sin4
2
22
0
aUM p 





= ∞
22
2
0
a
R
a
L
M
x
p
p ≈==
( )βαρπ += ∞ sin4
2
RUL
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

164. 164
Joukovsky Airfoils Design (continue – 3)
8. To Pitching Moment about Any Point x0 is given by:






+=+= ∞ Lmpp C
c
x
CcULxMM x
022
0 000
2
ρ 'yF
'xF 'xF
∞U
'x
L
α
plane−ς
'y
α
0pM
0x
απ 2sin4 22
0
aCc m =
( )βαπ += sin2LC
( )
( )





++≈






++=
∞
<<+
≈
∞
βαπαπ
ρ
βαπαπ
ρ
βα
a
x
aU
c
x
c
a
cUM
ac
px
022
1
4
0
2
2
22
88
2
sin22sin4
20






+





+





≈ ∞
<<+
≈
βαπ
ρβα
a
x
a
x
aUM
ac
px
0022
1
4
18
20
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

165. 165
Generation of Joukowsky Profiles through Conformal Mapping
Symmetric Joukowsky Profile
Circular Joukowsky Profile
Cambered Joukowsky Profile
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

166. 166
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

167. 167
Nikolay Yegorovich Joukovsky
(1847-1921
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

168. 168
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

169. 169
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

170. 170
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO

171. 171
Profile Theory Using Conformal Mapping
AERODYNAMICSSOLO
Return to Table of Content

172. 172
SOLO
- when the source moves at subsonic velocity V < a, it will stay inside the
family of spherical sound waves.
a
V
M
M
=





= −
&
1
sin 1
µ
Disturbances in a fluid propagate by molecular collision, at the sped of sound a,
along a spherical surface centered at the disturbances source position.
The source of disturbances moves with the velocity V.
- when the source moves at supersonic velocity V > a, it will stay outside the
family of spherical sound waves. These wave fronts form a disturbance
envelope given by two lines tangent to the family of spherical sound waves.
Those lines are called Mach waves, and form an angle μ with the disturbance
source velocity:
SHOCK & EXPANSION WAVES

173. 173
SOLO
SHOCK & EXPANSION WAVES
M < 1
M = 1
M > 1
Mach Waves

174. 174
SOUND WAVESSOLO
Sound Wave Definition:
∆ p
p
p p
p1
2 1
1
1=
−
<<
ρ ρ ρ2 1
2 1
2 1
= +
= +
= +
∆
∆
∆
p p p
h h h
For weak shocks
u
p
1
2
=
∆
∆ρ
1
1
11
1
1
1
1
1
2
1
2
1
1
uuuuuu
ρ
ρ
ρ
ρρρ
ρ
ρ
ρ ∆
−≅
∆
+
=
∆+
==)C.M.(
( ) ( ) ppuuupuupu ∆++




 ∆
−=+=+ 11
1
11122111
2
11
ρ
ρ
ρρρ)C.L.M.(
Since the changes within the sound wave are small, the flow gradients are small.
Therefore the dissipative effects of friction and thermal conduction are negligible
and since no heat is added the sound wave is isotropic. Since
au =1
s
p
a 





∂
∂
=
ρ
2
valid for all gases

175. 175
SPEED OF SOUND AND MACH NUMBERSOLO
Speed of Sound is given by
0=






∂
∂
=
ds
p
a
ρ
RT
p
C
C
T
dT
R
C
p
T
dT
R
C
d
dp
d
R
T
dT
Cds
p
dp
R
T
dT
Cds
v
p
v
p
ds
v
p
γ
ρ
ρ
ρ
ρ
ρ
===





⇒







=−=
=−=
=00
0
but for an ideal, calorically perfect gas
ρ
γγ
ρ p
RTa
TChPerfectyCaloricall
RTpIdeal
p
==






=
=
The Mach Number is defined as
RT
u
a
u
M
γ
==
∆
1
2
1
1
111
−−






=





=





=
γ
γ
γ
γ
γ
ρ
ρ
a
a
T
T
p
p
The Isentropic Chain:
a
ad
T
Tdd
p
pd
sd
1
2
1
0
−
=
−
==→=
γ
γ
γ
γ
ρ
ρ
γ

176. 176
SOLO
When a supersonic flow encounters a boundary the following will happen:
When a flow encounters a boundary it must satisfy the boundary conditions,
meaning that the flow must be parallel to the surface at the boundary.
- when the supersonic flow, in order to remain parallel to the boundary surface,
must “turn into itself” (see the Concave Corner example) a Oblique Shock will
occur. After the shock wave the pressure, temperature and density will increase.
The Mach number of the flow will decrease after the shock wave.
SHOCK & EXPANSION WAVES
- when the supersonic flow, in order to remain parallel to the boundary surface,
must “turn away from itself” (see the Convex Corner example) an Expansion
wave will occur. In this case the pressure, temperature and density will decrease.
The Mach number of the flow will increase after the expansion wave.
Return to Table of Content

177. 177
SHOCK WAVES
SOLO
A shock wave occurs when a supersonic flow decelerates in response to a sharp
increase in pressure (supersonic compression) or when a supersonic flow encounters
a sudden, compressive change in direction (the presence of an obstacle).
For the flow conditions where the gas is a continuum, the shock wave is a narrow region
(on the order of several molecular mean free paths thick, ~ 6 x 10-6
cm) across which is
an almost instantaneous change in the values of the flow parameters.
Shock Wave Definition )from John J. Bertin/ Michael L. Smith,
“Aerodynamics for Engineers”, Prentice Hall, 1979, pp.254-255(
When the shock wave is normal to the streamlines it is called a Normal Shock Wave,
otherwise it is an Oblique Shock Wave.
The difference between a Shock Wave and a Mach Wave is that:
- A Mach Wave represents a surface across which some derivative of the flow variables
(such as the thermodynamic properties of the fluid and the flow velocity) may be
discontinuous while the variables themselves are continuous. For this reason we call
it a Weak Shock.
- A Shock Wave represents a surface across which the thermodynamic properties and the
flow velocity are essentially discontinuous. For this reason it is called a Strong Shock.

178. 178
Normal Shock Wave Over a Blunt Body
Normal Shock
Wave
SHOCK WAVESSOLO
Oblique
Shock
Wave
Oblique Shock Wave Return to Table of Content

179. 179
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Conservation of Mass )C.M.( ρ ρ1 1 2 2u u= η
ρ
ρ
= =2
1
1
2
u
u
Conservation of Linear Momentum )C.L.M.( 2
2
221
2
11 pupu +=+ ρρ ( )
p
p
u
p
2
1
1
2
1
1
1 1= + −
ρ
η
H H h u h u1 2 1 1
2
2 2
21
2
1
2
= → + = +
h
h
u
h
2
1
1
2
1
2
1
2
1
1
= + −






η
Conservation of Energy )C.E.(
Field Equations
Constitutive Relations
p R T= ρIdeal Gas
( )
( )
( )
e e T C Tv= =
1 2
(1) Thermally Perfect Gas
)2( Calorically Perfect Gas
ργ
γ
ρρρ
γ
ρ
pp
C
C
C
C
p
R
C
TC
p
eh
v
p
vp C
C
v
p
v
p
CCR
p
TRp
p
11 −
=
−
===+=
≡−==
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2

180. 180
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
First Way
h
h
p
p
p
p
p
p
u
h
u
p
2
1
2
2
1
1
2
1
1
2
2
1
1
2
1
2
1
2
1
1
2
1
1
1
1
2
1
1
1
2
1
1
1
=
−
−
= = = + −





 = +
−
−






γ
γ ρ
γ
γ ρ
ρ
ρ η η γ
γ ρ
η
or
( )
p
p
u
p
u
p
C L M
2
1
1
2
1
1
1
2
1
1
2
1
1 1
1
1
2
1
1
1
η
ρ
η
η γ
γ ρ
η
= + −










= +
−
−






( . . .)
after further development we obtain
1 2
1
1
1
1
1
1
2
01
2
1
1
2
1
2
1
1
1
2
1
1
−
−





 − +










+ +
−










=
γ
γ
ρ
η
ρ
η
γ
γ
ρ
u
p
u
p
u
p
Solving for 1/η , we obtain
1
1 1 2
1
1
1
2
1
1
2
2
1
1
2
1
1
1
2
1
1
2
1
2
1
1
1
2
1
1
η
ρ
ρ
ρ ρ
γ
γ
ρ
γ
γ
ρ
γ
γ
= = =
+










− +










−
+
+
−










+
u
u
u
p
u
p
u
p
u
p
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2

181. 181
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
We obtain an other relation in the following way:
( )
p
p
u
p
p
p
u
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
2
1
1
2
1
1
2
2
1
1
2
1
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
1
1
1
2
1
1
1 1
1
1
1
1
2
1
1
1 1
2
1
2
1
1
2
1
1
2
1
2
1
2
1
2
η
γ
γ
ρ
η
ρ
η
η γ
γ η
η
γ
γ
γ
γ
γ
γ
η
γ
γ
γ
γ
γ
γ
γ
γ
− =
−
−






− = −








⇒
−
−
=
−
+






⇓
−
−
−
−




 = +
−
−






⇓
=
+
−
−
−
+
+
η
ρ
ρ
γ
γ
γ
γ
= = =
+
−
−
+
+
−
=2
1
1
2
2
1
2
1
2
1
1
2
1
1
1
1
1
u
u
p
p
p
p
p
p
T
T
or
Rankine-Hugoniot Equation
Rankine-Hugoniot Equation )1(
William John Macquorn
Rankine
(1820-1872)
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2
Pierre-Henri Hugoniot
(1851 – 1887)

182. 182
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
η
ρ
ρ
γ
γ
γ
γ
= = =
+
−
−
+
+
−
=2
1
1
2
2
1
2
1
2
1
1
2
1
1
1
1
1
u
u
p
p
p
p
p
p
T
T Rankine-Hugoniot Equation
Rankine-Hugoniot Equation )2(
p
p
2
1
2
1
2
1
1
1
1
1
1
=
+
−
−
+
−
−
γ
γ
ρ
ρ
γ
γ
ρ
ρ
T
T
p
p
p
p
p
p
p
p
p
p
p
p
2
1
2
1
1
2
2
1
2
1
2
1
2
1
2
1
2
1
2
1
1
2
2
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
= =
+
+
−
+
−
−
=
+
+
−
+
−
−
=
+
−
−
+
−
−
=
+
−
−
+
−
−
ρ
ρ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
ρ
ρ
γ
γ
ρ
ρ
ρ
ρ
γ
γ ρ
ρ
γ
γ
ρ
ρ
p2
p 1
ρ 2
ρ 1
NormalShockWave
Rankine-Hugoniot
Isentropic
γp2
p 1
ρ 2
ρ 1
( )=
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2

183. 183
Rankine-Hugoniot Equation )3(
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2
SOLO

184. 184
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Strong Shock Wave Definition:
p
p
u
u
T
T
p
p
R H R H
2
1
2
1
1
2
2
1
2
1
1
1
1
1
→ ∞ ⇒ = →
+
−
→
−
+
− −ρ
ρ
γ
γ
γ
γ
Weak Shock Wave Definition:
∆ p
p
p p
p1
2 1
1
1=
−
<<
ρ ρ ρ2 1
2 1
2 1
= +
= +
= +
∆
∆
∆
p p p
h h h
For weak shocks
u
p
1
2
=
∆
∆ρ
∆
∆
h u
ρ ρ
= 1
2
1
u u u u u u2
1
2
1
1
1
1
1
1 1
1
1
1
1
= =
+
=
+
≅ −
ρ
ρ
ρ
ρ ρ ρ
ρ
ρ
ρ∆ ∆
∆
)C.M.(
( ) ( )ρ ρ ρ
ρ
ρ
1 1
2
1 1 1 2 2 1 1 1
1
1 1u p u u p u u u p p+ = + = −





 + +
∆
∆)C.L.M.(

ordernd
uuuhhuuhhuhuh
2
4
1
2
1
2
1
2
1
2
1 2
1
2
1
2
1
1
2
11
2
1
1
11
2
22
2
11 




 ∆
+
∆
−+∆+=




 ∆
−+∆+=+=+
ρ
ρ
ρ
ρ
ρ
ρ)C.E.(
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2

185. 185
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Second Way
h h u h u0 1 1
2
2 2
21
2
1
2
≡ + = +Define







−
−
−
=→+
−
=
−
−
−
=→+
−
=
2
10
1
12
1
1
1
0
2
20
2
22
2
2
2
0
11
2
1
1
11
2
1
1
uh
p
u
p
h
uh
p
u
p
h
γ
γ
γ
γ
ρργ
γ
γ
γ
γ
γ
ρργ
γ
u u h1 2 0
2
1
1
=
−
+
γ
γ
Prandtl’s Relation
( )u h
u
u
u
p
p
u
p2 0
1
2 1
1
2
2
1
1
2
1
1
2
1
1
1
1 1=
−
+
→ = = → = + −
γ
γ
ρ ρ ρη
ρ
ηFrom this relation, we obtain:
Prandtl’s Relation
Ludwig Prandtl
(1875-1953)
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2
)C.M.(
)C.L.M.(
ργ
γ p
h
1−
=
and use
12
22
2
11
1
2211
2
2
221
2
11 11
uu
u
p
u
p
uu
pupu
−=−→



=
+=+
ρρρρ
ρρ
1221
21
0
2
1
2
1111
uuuu
uu
h −=
−
+
−
−





−
−
γ
γ
γ
γ
γ
γ
( ) 




 −
−−=
−−
γ
γ
γ
γ
2
1
1
1
12
21
12
0 uu
uu
uu
h

186. 186
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
)C.M.(
Hugoniot Equation
ρ ρ
ρ
ρ
1 1 2 2 2 1
1
2
u u u u= → =
( )ρ ρ ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ ρ
ρ ρ
ρ
ρ ρ ρ
ρ
ρ
ρ
ρ
ρ
ρ
1 1
2
1 2 2
2
2 2
1
2
2
1
2
2 2 1 1
2
1
1
2
2
1
2 1
2
2 1
1
2 2 1
2
2
2
2 2 1
2
1
2
2 1
1
2
2 1
1
2
u p u p u p p p u u
u
p p
u
p p
u u
u u
+ = + =





 + → − = −





 = − →
→ =
−
−





 → =
−
−














=
=
)C.L.M.(
( )( )
h u h u e
p p p
e
p p p
e e
p p p p p p p p
e e
p p
h e
p
1 1
2
2 2
2
1
1
1
2 1
2 1
2
2
2
2
2 1
2 1
1
2
2 1
2 1
2 1
2 1
2
1
1
2
2
2 1
2 1
2
2
1
2
1 2
1 2 2 1
2
2 1
2 1 1 2
1
2
1
2
1
2
1
2
1
2
+ = + → + +
−
−





 = + +
−
−





 →
→ − =
−
−
−





 + − =
−
−
−
+
−
→
→ − =
− +
= +
ρ
ρ ρ ρ
ρ
ρ ρ ρ ρ
ρ
ρ
ρ ρ
ρ
ρ
ρ
ρ ρ ρ ρ ρ
ρ ρ
ρ ρ
ρ ρ
ρρ
ρ ρ
( ) ( )
+ −
=
+ − − + −
→
→ − =
+ − +














2 2
2
2 2
2
2
1 2 2
1 2
2 2 2 1 2 1 1 1 2 2
1 2
2 1
2 1 2 1 1 2
1 2
p p p p p p p p
e e
p p p p
ρ ρ
ρ ρ
ρ ρ ρ ρ ρ ρ
ρ ρ
ρ ρ
ρ ρ
)C.E.(
e e
p p
2 1
1 2
2 1
2
1 1
− =
+
−






ρ ρ
Hugoniot Equation
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2

187. 187
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Fanno’s Line for a Perfect Gas )1(
( )1 1 1 2 2ρ ρu u
m
A
= =

( ) frictionpupu ++=+ 2
2
221
2
112 ρρ
( )3
1
2
1
2
1 1
2
2 2
2
C T u C T u h C Tp p p+ = + =
( )4 1 1 1 2 2 2
p R T p R T= =ρ ρ
( )5 2 1
2
1
2
1
s s C
T
T
R
p
p
p
− = −ln ln
(C.M.)
(C.L.M.)
(C.E.)
Ideal Gas
( )
p
p
T
T
u
u
h C T
h C T
p
p
T
T
h C T
h C T
s s C
T
T
R
T
T
h C T
h C T
p
p
p
p
p
p
p
2
1
4
2
1
2
1
2
1
1
1
2
3
0 1
0 2
2
1
2
1
0 1
0 2
2 1
2
1
2
1
0 1
0 2
5
=












= =
−
−







→ =
−
−
→
− = −
−
−
( )
( ) ( )
ln ln
ρ
ρ
ρ
ρ
Assume that all the conditions
of the model are satisfied except
the moment equation (2)
(a flow with friction)
Using , we obtainh C Tp=
s
s 1
s 2
s max
h 1
h 2
h
2
1
s s C
h
h
R
h
h
h h
h h
p2 1
2
1
2
1
0 1
0 2
− = −
−
−
ln ln
Fanno’s Line for a Perfect Gas
This is the Adiabatic, Constant Area Flow.
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2
Gino Girolamo Fanno
(1888 – 1962)

188. 188
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Fanno’s Line for a Perfect Gas )2(
s
s 1
s 2
s max
h 1
h 2
h
2
1
We have a point of maximum entropy. Let see the significance of this point
ρρ
dp
dh
dp
dhdsT =→=−= 0
max
Gibbs
u
dud
dudu −=→=+
ρ
ρ
ρρ 0)C.M.(
duudh
u
hd −=→=





+ 0
2
2
)C.E.(
Therefore
)4..(
0
.).(
00
0
EC
ds
MC
dsds
ds
u
du
d
dpd
d
dpdp
dh =





−





=





==
===
=
ρρ
ρ
ρρ
0
0
=
= 





=
ds
ds
d
dp
u
ρ
or
ds C
dT
T
R
dp
p
ds C
dT
T
R
d
C
C
dp
p
d
dp
d p
dp
d
p
R T
p
v
p
v
ds
ds
ds ds
p R T
= − =
= − =







→ ≡ = = → = ==
=
= =
=
max
max
0
0
0
0
0 0
ρ
ρ
γ
ρ
ρ
ρ
ρ
ρ
γ
ρ
γ
ρ
We have:
u
dp
d
R T a speed of soundds
ds
=
=
=





 = = =0
0
ρ
γ
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
1
1
1
1
1
2
2
2
2
2
1 2

189. 189
Ideal Gas
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Rayleigh’s Line for a Perfect Gas )1(
( )
A
m
uu

== 22111 ρρ
( )2 1 1
2
1 2 2
2
2ρ ρu p u p+ = +
( ) QhuTCuTC pp ++=+ 2
22
2
11
2
1
2
1
3
( )4 1 1 1 2 2 2
p R T p R T= =ρ ρ
( )5 2 1
2
1
2
1
s s C
T
T
R
p
p
p
− = −ln ln
(C.M.)
(C.L.M.)
(C.E.)
Assume that all the conditions
of the model are satisfied except
the energy equation (3)
(a flow with heating and cooling)
Let substitute in (5) , to obtainh C Tp=
Rayleigh’s Line for a Perfect Gas
This is the Frictionless, Constant Area Flow, with Cooling and Heating.
s max
s
s 1
s 2
h 1
h 2
h
M>1
M<1
Rayleigh2
1
Heating
Heating
Cooling
 m
A
R T
p
p
m
A
R T
p
p
x
p
1
1
1
2
2
2
1
+ = +
( )
2
1
12
1
1
1
2
12
11
1
2
12
&1
2
1
lnln5
p
R
A
m
c
p
TR
A
m
b
h
C
a
bbR
h
h
Css
p
p

=







+=








−+−=−
We want to find x
p
p
≡ 2
1
. Let multiply the result by
x
p1
x
m
A
R T
p
b
x
m
A
R
p
c
T2 1
1
2
1
1
2
1
21
2
0− +





 + =
 
   
or
x
p
p
b b a T= = + −2
1
1 1
2
1 2
The solution is:
John William
Strutt
Lord Rayleigh
)1842-1919(
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
Q
1
1
1
1
1
2
2
2
2
2
1 2

190. 190
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Rayleigh’s Line for a Perfect Gas )2(
We have a point of maximum entropy. Let see the significance of this point
u
dud
dudu −=→=+
ρ
ρ
ρρ 0)C.M.(
)C.L.M.(
A Normal Shock Wave must be on both Fanno and Rayleigh Lines, therefore
the end points of a Normal Shock Wave must be on the intersection of
Fanno and Rayleigh Lines
u
dp
d
R T a speed of soundds
ds
=
=
=





 = = =0
0
ρ
γ
d p u
dp
du
u+





 = → = −
1
2
02
ρ ρ
( )→ = = − −





 =
dp
d
dp
du
du
d
u
u
u
ρ ρ
ρ
ρ
2
s
s 1
s 2
h 1
h 2
h
M>1
M<1
Rayleigh
Fanno
2
1
SHOCK
According to the Second Law of Thermodynamics
the Entropy must increase. Therefore a Normal Shock
Wave from state (1) to state (2) must be such that
s2 > s1. (from supersonic to subsonic flow only)
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
Q
1
1
1
1
1
2
2
2
2
2
1 2

191. 191
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Mach Number Relations )1(
( )
( )
( )
 
C M u u
C L M u p u p
p
u
p
u
u u
C E
a
h
u
a
h
u
a a u
a a u
a
p
. .
. . .
. .
ρ ρ
ρ ρ ρ ρ
γ γ
γ γ
γ γ
γ
ρ
1 1 2 2
1 1
2
1 2 2
2
2
1
1 1
2
2 2
2 1
1
2
1
1
2 2
2
2
2
2
1
2 2
1
2
2
2 2
2
2
4
1
1
2 1
1
2
1
2
1
2
1
2
1
2
=
+ = +



→ − = − →
−
+ =
−
+ →
=
+
−
−
=
+
−
−














=
∗
∗



− = −
a
u
a
u
u u1
2
1
2
2
2
2 1
γ γ
Field Equations:
( )
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
+
−
−
−
+
+
−
= −
↓
+ −
+
−
− = − →
+
= −
−
=
+
↓
∗ ∗
∗
∗
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
1
2
1
2
2
1
1
2
2
2 2 1
2 1
1 2
2
2 1 2 1
2
1 2
a
u
u
a
u
u u u
u u
u u
a u u u u
a
u u
u u a1 2
2
= ∗
u
a
u
a
M M1 2
1 21 1∗ ∗
∗ ∗
= → =
Prandtl’s Relation
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
Q
1
1
1
1
1
2
2
2
2
2
1 2
Ludwig Prandtl
(1875-1953)

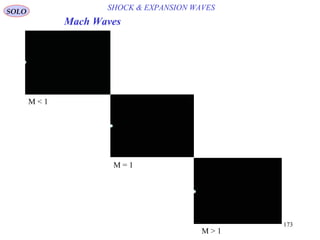
192. 192
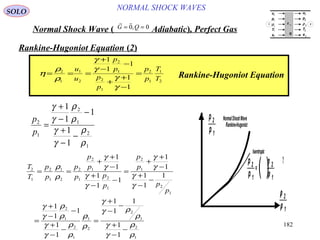
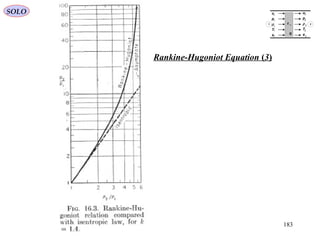
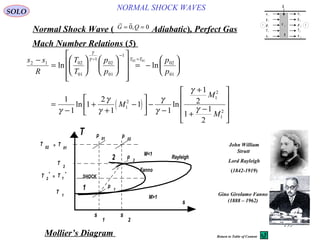
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Mach Number Relations )2(
( ) ( ) ( ) ( )
( )
( )
( )
( )
( )[ ]
( )( ) ( )
M
M
M
M
M
M
M
M
M
2
2
2
2
1
1
2
1
2
1
2
1
2
1
2
2
1
1
2
1 1
2
1
1
1 2
1
2 1 2
1 1 1 1 1
1
2
=
+
− −
=
+ − −
=
+
+
− +
− −
=
− +
+ / + − / / + − / + − −
∗
=
∗
∗
∗
γ
γ γ γ
γ
γ
γ
γ
γ
γ γ γ γ γ
or
( )
M
M
M
M
M
H H
A A
2
1
2
1
2
1
2
1
21 2
1 2
1
1
2
1
2
2
1
1
1
2
1
2
1
1
=
+
−
−
−
=
+
+
−
+
+
−
=
=
γ
γ
γ γ
γ
γ
γ
( )
( )
ρ
ρ
γ
γ
2
1
1
2
1
2
1 2
1
2
2 1
2 1
2
1
2
1 2 1
1 2
= = = = =
+
− +
=
∗
∗
A A u
u
u
u u
u
a
M
M
M
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
Q
1
1
1
1
1
2
2
2
2
2
1 2

193. 193
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Mach Number Relations )3(
( )
( )
( ) ( )
( )
p
p
u
p
u
u
u
a
M
M
M
M
M M
M
2
1
1
2
1
1
2
1
1
2
1
2
1
2
1
2 1
2
1
2 1
2 1
2
1
2
1
2
1 1 1 1
1 1
1 2
1
1
1 1 2
1
= + −





 = + −






= + −
− +
+





 = +
/ + − / − −
+
ρ
γ
ρ
ρ
γ
γ
γ
γ
γ γ
γ
or
)C.L.M.(
( )
p
p
M2
1
1
2
1
2
1
1= +
+
−
γ
γ
( )
( )
( )
h
h
T
T
p
p
M
M
M
a
a
h C T p RTp
2
1
2
1
2
1
1
2
1
2 1
2
1
2
2
1
1
2
1
1
1 2
1
= = = +
+
−






− +
+
=
= =ρ ρ
ρ
γ
γ
γ
γ
( )
( )
( )
s s
R
T
T
p
p
M
M
M
2 1 2
1
1
2
1
1
1
2
1
1
1
2
1
2
1
1
2
1
1
1 2
1
−
=






















= +
+
−






− +
+
















−
−
− −
ln ln
γ
γ
γ
γ
γ
γ
γ
γ
γ
γ
( )
( )
( )
( )
s s
R
M M
M
2 1
1 1
2 1
2 3
2
2 1
2 41
2
2
3 1
1
2
1
1
−
≈
+
− −
+
− +
− << γ
γ
γ
γ
K Shapiro p.125
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
Q
1
1
1
1
1
2
2
2
2
2
1 2

194. 194
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Mach Number Relations )4(
( )
p
p
p
p
p
p
p
p
M
M
M02
01
02
2
1
01
2
1
2
2
1
2
1
1
2
1
1
2
1
1
2
1
2
1
1= =
+
−
+
−










+
+
−






−γ
γ
γ
γ
γ
γ
( )
( )
1
1
2
1
1
2
1
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
1
1
2
1
2
1
1
2
2
1
2
1
2
1
2
2
1
2
1
2
1
2
1
2
+
−
= +
−
+
−
−
−
=
−
−
+
−
+
−





+
+
+
−






=
+
+
+
−
γ γ
γ
γ
γ
γ
γ γ γ
γ γ
γ
γ
γ
γ
M
M
M
M M
M
M
M
( )
( )
p
p
M
M
M02
01
1
2
1
2
1
1
2
1
1
1
2
1
2
1
1
1
2
1
1=
+
+
+
−












+
+
−






−
−
−
γ
γ
γ
γ
γ
γ
γ
γ
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
Q
1
1
1
1
1
2
2
2
2
2
1 2

195. 195
NORMAL SHOCK WAVESSOLO
Normal Shock Wave ) Adiabatic(, Perfect Gas
 
G Q= =0 0,
Mach Number Relations )5(
( )
s s
R
T
T
p
p
p
p
M
M
M
T T
2 1 02
01
1
02
01
1
02
01
1
2
1
2
1
2
02 01
1
1
1
2
1
1
1
1
2
1
1
2
−
=






















= −






=
−
+
+
−





 −
−
+
+
−










−
−
=
ln ln
ln ln
γ
γ
γ
γ
γ
γ
γ
γ
γ
s
s
1
s
2
T
M>1
M<1
Rayleigh
Fanno
2
1
SHOCK
T
2
T
1
T
02
T
01=
T 2
T 1=* *
p
2
p
1
p
01
p
02
Mollier’s Diagram
u
p
ρ
T
e
u
p
ρ
T
e
τ 11
q
Q
1
1
1
1
1
2
2
2
2
2
1 2
John William
Strutt
Lord Rayleigh
)1842-1919(
Gino Girolamo Fanno
(1888 – 1962)
Return to Table of Content

196. 196
OBLIQUE SHOCK & EXPANSION WAVESSOLO
→→
→→
+=
+=
twnuV
twnuV
11
11
222
111


Continuity Eq.: 2211 uu ρρ =
( ) ( ) ( )21222111 ppuuuu +−−=+− ρρ
Moment Eq. Tangential Component:
( ) ( ) 0222111 =+− wuwu ρρ
Moment Eq. Normal Component:
Energy Eq.: 22
2
2
2
2
211
2
1
2
1
1
22
u
wu
hu
wu
h ρρ 






 +
+=






 +
+
Continuity Eq.: 2211 uu ρρ =
Moment Eq.:
21 ww =
2
222
2
111 upup ρρ +=+
Energy Eq.:
22
2
2
2
2
1
1
u
h
u
h +=+
Summary
Calorically Perfect Gas:
Tch
TRp
p=
= ρ
6 Equations with 6 Unknowns
222222 ,,,,, hwuTpρ

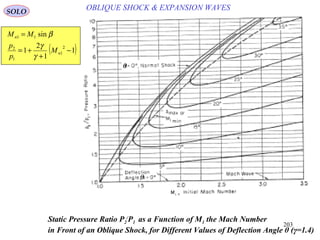
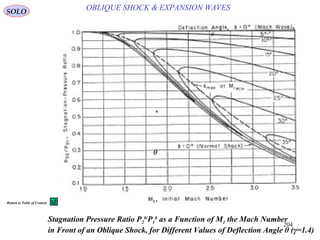
197. 197
OBLIQUE SHOCK & EXPANSION WAVESSOLO
For a calorically Perfect Gas
( )
( )
( )
( )[ ]
( )[ ]
2
1
1
2
1
2
2
1
2
12
2
2
1
1
2
2
1
2
1
1
2
11/2
1/2
1
1
2
1
21
1
ρ
ρ
γγ
γ
γ
γ
γ
γ
ρ
ρ
p
p
T
T
M
M
M
M
p
p
M
M
n
n
n
n
n
n
=
−−
−+
=
−
+
+=
+−
+
=
βsin11 MMn =
( )θβ −
=
sin
2
2
nM
M
Now we can compute
( )
( ) ( )
( )
( )
( )






⋅+
−
=
−
+
−+
===
−
⇒









=
=−
=
θββ
θβ
β
θβ
βγ
βγ
ρ
ρ
β
θβ
θβ
β
tantan1tan
tantan
tan
tan
sin1
sin12
tan
tan
tan
tan
22
1
22
1
2
1
1
2
12
2
2
1
1
M
M
u
u
ww
w
u
w
u

198. 198
OBLIQUE SHOCK & EXPANSION WAVESSOLO
( ) 





++
−
=
22cos
1sin
cot2tan 2
1
22
1
βγ
β
βθ
M
M
M,, βθ relation
12 <M
12 >M
.5max =Mforθ
β θ
1M 2M
Strong Shock
Weak Shock
θ
β

199. 199
OBLIQUE SHOCK & EXPANSION WAVESSOLO
1. For any given M1 there is a maximum deflection angle θmax
If the physical geometry is such that θ > θmax, then no solution
exists for straight oblique shock wave. Instead the shock will be
curved and detached.

200. 200
OBLIQUE SHOCK & EXPANSION WAVESSOLO
2. For any given θ < θmax, there are two values of β predicted by
the θ-β-M relation for a given Mach number.
WEAKβ
STRONGβ
( ) 





++
−
=
22cos
1sin
cot2tan 2
1
22
1
βγ
β
βθ
M
M
M,, βθ relation
- the large value of β is called the strong shock solution
In nature the weak shock solution usually occurs.
- the small value of β is called the weak shock solution
- in the strong shock solution M2 is subsonic (M2 < 1)
- in the weak shock M2 solution is supersonic (M2 > 1)

201. 201( ) 





++
−
=
22cos
1sin
cot2tan 2
1
22
1
βγ
β
βθ
M
M
M,, βθ relation
SOLO
OBLIQUE SHOCK & EXPANSION WAVES
θ
β
4.1=γ
θ
maxθ
θ

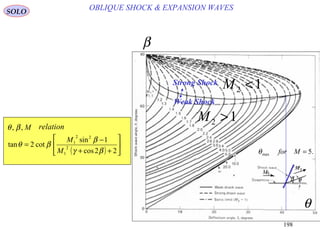
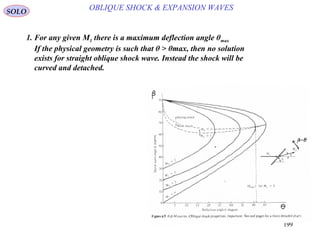
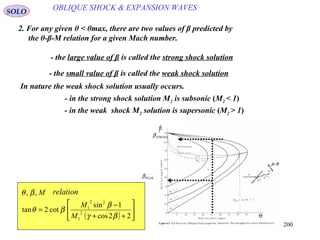
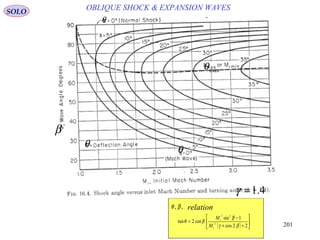
202. 202
( )[ ]
( )[ ]
( )θβ
γγ
γ
β
−
=
−−
−+
=
=
sin
11/2
1/2
sin
2
2
2
1
2
12
2
11
n
n
n
n
n
M
M
M
M
M
MM
SOLO
θ
maxθ
OBLIQUE SHOCK & EXPANSION WAVES
Mach Number in Back of Oblique Shock M2 as a Function of the Mach Number
in Front of the Shock M , for Different Values of Deflection Angle θ (γ=1.4)

203. 203
( )1
1
2
1
sin
2
1
1
2
11
−
+
+=
=
n
n
M
p
p
MM
γ
γ
β
SOLO
θ
θ
OBLIQUE SHOCK & EXPANSION WAVES
Static Pressure Ratio P2
/
P1 as a Function of M1 the Mach Number
in Front of an Oblique Shock, for Different Values of Deflection Angle θ (γ=1.4)

204. 204
SOLO
θ
θ
OBLIQUE SHOCK & EXPANSION WAVES
Stagnation Pressure Ratio P2
0/
P1
0
as a Function of M1 the Mach Number
in Front of an Oblique Shock, for Different Values of Deflection Angle θ (γ=1.4)
Return to Table of Content

205. 205
SOLO
OBLIQUE SHOCK & EXPANSION WAVES
Prandtl-Meyer Expansion Waves
Ludwig Prandtl
(1875 – 1953)
Theodor Meyer
(1882 – 1972)
The Expansion Fan depicted in Figure was
First analysed by Prandtl in 1907 and his
student Meyer in 1908.
Let start with an Infinitesimal Change across a
Mach Wave
M
ach
W
ave
θd
µ µ
π
−
2
θµ
π
d−−
2
V
VdV +
( )
( ) θµθµ
µ
θµπ
µπ
dddV
VdV
sinsincoscos
cos
2/sin
2/sin
−
=
−−
+
=
+
µ
θµθ
µθ tan
/
tan1
tan1
1
1
VVd
dd
dV
Vd
=⇒+≈
−
≈+
1
1
tan
1
sin
2
1
−
=⇒





= −
MM
µµ
V
Vd
Md 12
−=θ

206. 206
SOLO
OBLIQUE SHOCK & EXPANSION WAVES
Prandtl-Meyer Expansion Waves (continue-1)
M
ach
W
ave
θd
µ µ
π
−
2
θµ
π
d−−
2
V
VdV +
V
Vd
Md 12
−=θ
Integrating this equation gives
∫ −=
2
1
12
M
M
V
Vd
Mθ
Using the definition of Mach Number: V = M.
a
a
ad
M
Md
V
Vd
+=
For a Calorically Perfect Gas
20
2
0
2
1
1 M
T
T
a
a −
+==




 γ
MdMM
a
ad
1
2
2
1
1
2
1
−





 −
+
−
−=
γγ
M
Md
MV
Vd
2
2
1
1
1
−
+
=
γ ∫ −
+
−
=
2
1
2
2
2
1
1
1
M
M
M
Md
M
M
γ
θ

207. 207
SOLO
OBLIQUE SHOCK & EXPANSION WAVES
Prandtl-Meyer Expansion Waves (continue-2)
The integral
∫ −
+
−
=
2
1
2
2
2
1
1
1
M
M
M
Md
M
M
γ
θ
( ) ∫ −
+
−
=
M
Md
M
M
M
2
2
2
1
1
1
γ
ν
is called the Prandtl-Meyer Function and is
given the symbol ν. Performing the integration we obtain
( ) ( ) ( )1tan1
1
1
tan
1
1 2121
−−−
+
−
−
+
= −−
MMM
γ
γ
γ
γ
ν
Deflection Angle ν and Mach Angle μ as functions of Mach Number






= −
M
1
sin 1
µ
Finally
( ) ( )12 MM ννθ −=
Return to Table of Content

208. 208
Linearized Flow Equations
1. Irrotational Flow
SOLO
Assumptions
2. Homentropic
3. Thin bodies
( )0

=×∇ u






=
∂
∂
=∇ 0&0..;.
t
s
seieverywhereconsts
This implies also inviscid flow ( )~τ = 0
Changes in flow velocities due to body presence are small
were
- flow velocity as a function of position and time
- flow entropy as a function of position and time
( )tzyxu ,,,

( )tzyxs ,,,

209. 209
SOLO
(C.L.M)
For an inviscid flow conservation of linear momentum gives:( )~τ = 0
Assume that body forces are conservative and stationary
were
- flow pressure as a function of position and time( )tzyxp ,,,
- flow density as a function of position and time( )tzyx ,,,ρ
( ) Gpuuu
t
u
uu
t
u
tD
uD 



ρ
∂
∂
ρ
∂
∂
ρρ +−∇=





×∇×−





∇+=





∇⋅+= 2
2
1
or
( ) G
p
uuu
t
u 

+
∇
−=×∇×−





∇+
∂
∂
ρ
2
2
1 Euler’s Equation
0& =
∂
Ψ∂
Ψ−∇=
t
G

- Body forces as a function of position( )zyxG ,,

Leonhard Euler
1707-1783
Linearized Flow Equations

210. 210
SOLO
Let integrate the Euler’s Equation between two points (1) and (2)
( ) ( ) ( ) ∫∫∫∫∫∫ ⋅Ψ∇+
⋅∇
+×∇⋅×−⋅





∇+⋅
∂
∂
=⋅





Ψ∇+
∇
+×∇×−





∇+
∂
∂
=
2
1
2
1
2
1
2
1
2
2
1
2
1
2
2
1
2
1
0 rd
rdp
uurdrdurdu
t
rd
p
uuuu
t



υρ
We can chose the path of integration as follows:
- along a streamline ( and are collinear; i.e.: )rd

u

0

=×urd
- along any path, if the flow is irrotational ( )0

=×∇ u
to obtain:
( ) ( ) 0
2
1
=×∇⋅×∫ uurd

Assuming that the flow is irrotational we can define a potential ,
such that:
( )0

=×∇ u ( )tr ,

Φ
Φ∇=u

Let use the identity
to obtain:
( ) rdFtrFd constt

⋅∇==
,
( )
2
1
2
2
1
2
2
1
2
1
0








Ψ+++
∂
Φ∂
=





Ψ∇++





+Φ
∂
∂
= ∫∫
∞
p
p
pd
u
t
pd
udd
t ρρ
Bernoulli’s Equation
for Irrotational
and Inviscid Flow
Daniel Bernoulli
1700-1782
Linearized Flow Equations

211. 211
SOLO
For an isentropic ideal gas we have
2
2
11 a
ad
T
Tdd
p
pd
−
=
−
==
γ
γ
γ
γ
ρ
ρ
γ
where
ρ
γ
γ
ρρ
p
TR
d
pdp
a
s
===
∂
∂
=2
is the square of the speed of sound
In this case
2
2
2
1
1
1 2
ad
a
adppd
RTa
RTp
−
=
−
=
=
=
γργ
γ
ρ γ
ρ
and
[ ]222
1
1
1
1
2
2
∞−
−
=
−
= ∫∫
∞∞
aaad
pd
a
a
p
p
γγρ
Using the Bernoulli’s Equation we obtain
( ) ( ) ( ) ( )





Ψ−Ψ+−+
∂
Φ∂
−−=−=− ∞∞∞ ∫
∞
2222
2
1
11 Uu
t
dp
aa
p
p
γ
ρ
γ
( )
2
1
2
2
1
2
2
1
2
1
0








Ψ+++
∂
Φ∂
=





Ψ∇++





+Φ
∂
∂
= ∫∫
∞
p
p
pd
u
t
pd
udd
t ρρ
Bernoulli’s Equation
for Irrotational
and Inviscid Flow
Linearized Flow Equations

212. 212
SOLO
Let use the conservation of mass (C.M.) equation
(C.M.) 0=⋅∇+ u
tD
D 
ρ
ρ
or
tD
D
u
ρ
ρ
1
−=⋅∇

Let go back to Bernoulli’s Equation ( ) ( )





Ψ−Ψ+−+
∂
Φ∂
−= ∞∞∫
∞
22
2
1
Uu
t
pd
p
p
ρ
and use the Leibnitz rule of differentiation: ( ) ( )uxFdxuxF
xd
d
x
x
,,
0
=∫
to obtain
ρρ
1
=∫
∞
p
p
pd
pd
d
Now we can compute tD
Da
tD
D
d
pd
tD
pD
tD
pDpd
pd
dpd
tD
D
p
p
p
p
ρ
ρ
ρ
ρρρρρ
2
11
===








= ∫∫
∞∞
Therefore ( ) ( )





Ψ−Ψ+−+
∂
Φ∂
=−=−=⋅∇ ∞∞∫
∞
22
22
2
1111
Uu
ttD
D
a
pd
tD
D
atD
D
u
p
p
ρ
ρ
ρ

Since ( )[ ] 0=Ψ−Ψ= ∞∞
tD
D
u
tD
D
we have












∇⋅+
∂
∂
⋅+
∂
Φ∂
=











∇⋅+
∂
Φ∂
∇⋅+
∂
∂
⋅+
∂
Φ∂
=
=





+
∂
Φ∂






∇⋅+
∂
∂
=





+
∂
Φ∂
=⋅∇
Φ∇=
2
2
1
2
1
2
11
2
11
2
2
2
2
2
2
2
2
2
2
2
2
u
u
t
u
u
ta
u
u
t
u
t
u
u
ta
u
t
u
ta
u
ttD
D
a
u
u 






GOTTFRIED WILHELM
von LEIBNIZ
1646-1716
Linearized Flow Equations

213. 213
SOLO












∇⋅+
∂
∂
⋅+
∂
Φ∂
=











∇⋅+
∂
Φ∂
∇⋅+
∂
∂
⋅+
∂
Φ∂
=
=





+
∂
Φ∂






∇⋅+
∂
∂
=





+
∂
Φ∂
=⋅∇
Φ∇=
2
2
1
2
1
2
11
2
11
2
2
2
2
2
2
2
2
2
2
2
2
u
u
t
u
u
ta
u
u
t
u
t
u
u
ta
u
t
u
ta
u
ttD
D
a
u
u 






Let substitute Φ∇=u













Φ∇⋅Φ∇∇⋅Φ∇+Φ∇
∂
∂
⋅Φ∇+
∂
Φ∂
=Φ∇⋅∇
2
1
2
1
2
2
2
tta
( ) ( ) ( )





Ψ−Ψ+−Φ∇⋅Φ∇+
∂
Φ∂
−−= ∞∞∞
222
2
1
1 U
t
aa γ
Special cases
0≈Φ∇⋅∇ Laplace’s equation
∞∞ >>Ua (subsonic flow) we can approximate
the first equation by
1
2 ( ) ( ) 2
2
t
uu
t
uuu
∂
Φ∂
<⋅
∂
∂
+⋅∇⋅
 we can approximate
the first equation by
0
1
2
2
2
=
∂
Φ∂
−Φ∇⋅∇
ta
Wave equation
Pierre-Simon
Laplace
1749-1827
Linearized Flow Equations

214. 214
SOLO
Note
The equation






+
∂
Φ∂






∇⋅+
∂
∂
=⋅∇ 2
2
2
11
u
t
u
ta
u

can be written as
Φ=





Φ∇⋅+
∂
Φ∂






∇⋅+
∂
∂
=





+
∂
Φ∂






∇⋅+
∂
∂
=Φ∇ 2
2
22
2
2
2 11
2
11
tD
D
a
u
t
u
ta
u
t
u
ta
c
c

where the subscript c on and on is intended to indicate that the velocity is
treated as a constant during the second application of the operators and .
cu

2
2
tD
Dc
t∂∂/ ( )∇⋅u

This equation is similar to a wave equation.
End Note
Linearized Flow Equations

215. 215
SOLO
Let compute the local pressure coefficient: 2
2
1
:
∞∞
∞−
=
U
pp
C p
ρ
We have:










−







=










−







=










−





=





−=
−
∞∞
=−
∞
∞
∞
=
−
∞
∞
∞






=
=
∞
∞
∞
∞
∞∞∞
−
∞∞
∞∞∞
1
2
1
2
1
1
2
1
2
1
2
2
2
/1
2
2
2
2
1
22
2
1
γ
γ
γ
γ
γ
γ
γ
ρ
γ
γ
ρ γ
γ
a
a
Ma
a
a
U
T
T
U
TR
p
p
U
p
C
aUMTRa
T
T
p
p
TRp
p
Let use the equation
( ) ( ) ( )





Ψ−Ψ+−Φ∇⋅Φ∇+
∂
Φ∂
−−= ∞∞∞
222
2
1
1 U
t
aa γ
to compute
( ) ( ) ( )





Ψ−Ψ+−Φ∇⋅Φ∇+
∂
Φ∂−
−= ∞∞
∞∞
2
22
2
2
11
1 U
taa
a γ
Finally we obtain:
( ) ( ) ( )










−












Ψ−Ψ+−Φ∇⋅Φ∇+
∂
Φ∂−
−=
−
∞∞
∞∞
1
2
11
1
2 1
2
22
γ
γ
γ
γ
U
taM
Cp
Linearized Flow Equations

216. 216
SOLO
Assuming a stationary flow and neglecting the body forces :





=
∂
∂
0
t
( )0=Ψ












Φ∇⋅Φ∇∇⋅Φ∇=Φ∇⋅∇
2
11
2
a
( ) ( )222
2
1
∞∞ −Φ∇⋅Φ∇
−
−= Uaa
γ
( ) ( )










−






−Φ∇⋅Φ∇
−
−=
−
∞
∞∞
1
2
1
1
2 1
2
22
γ
γ
γ
γ
U
aM
Cp
Φ∇=u

Linearized Flow Equations

217. 217
SOLO
1
0
332211
323121
=⋅=⋅=⋅
=⋅=⋅=⋅
→→→→→→
→→→→→→
eeeeee
eeeeee
General Coordinates ( )321 ,, uuu
→→→
∂
Φ∂
+
∂
Φ∂
+
∂
Φ∂
=Φ∇ 3
33
2
22
1
11
111
e
uh
e
uh
e
uh
( ) ( ) ( )





∂
∂
+
∂
∂
+
∂
∂
=






++⋅∇=⋅∇
→→→
321
3
213
2
132
1321
332211
1
Ahh
u
Ahh
u
Ahh
uhhh
eAeAeAA

Using we obtainΦ∇=:A













∂
Φ∂
∂
∂
+





∂
Φ∂
∂
∂
+





∂
Φ∂
∂
∂
=
=Φ∇⋅∇=Φ∇
33
21
322
13
211
32
1321
2
1
uh
hh
uuh
hh
uuh
hh
uhhh
where
We have for ( ) ( )321321 ,,,,, uuuAuuu

Φ
Linearized Flow Equations

218. 218
SOLO
zzyyxx Φ+Φ+Φ=Φ∇=Φ∇⋅∇ 2






Φ+Φ+Φ∇⋅





Φ+Φ+Φ=





Φ∇⋅Φ∇∇⋅Φ∇
→→→
222
2
1
2
1
2
1
111
2
1
zyxzyx zyx
( ) ( )
( )=ΦΦ+ΦΦ+ΦΦΦ+
ΦΦ+ΦΦ+ΦΦΦ+ΦΦ+ΦΦ+ΦΦΦ=
zzzyzyxzxz
yzzyyyxyxyxzzxyyxxxx
yzzyxzzxxyyxzzzyyyxxx ΦΦΦ+ΦΦΦ+ΦΦΦ+ΦΦ+ΦΦ+ΦΦ= 222
22












Φ∇⋅Φ∇∇⋅Φ∇=Φ∇⋅∇
2
11
2
a
( ) ( )222
2
1
∞∞ −Φ∇⋅Φ∇
−
−= Uaa
γ
( ) 0
12
2
22111
222
222
2
2
2
2
2
=Φ−ΦΦ+ΦΦ+ΦΦ−Φ
ΦΦ
−
Φ
ΦΦ
−Φ
ΦΦ
−Φ






 Φ
−+Φ







 Φ
−+Φ






 Φ
−
ttztzytyxtxyz
zy
xz
zx
xy
yx
zz
z
yy
y
xx
x
aaa
aaaaa
( ) ( ) ( )





Ψ−Ψ+−Φ+Φ+Φ+
∂
Φ∂
−−= ∞∞∞
222222
2
1
1 U
t
aa zyxγ
We finally obtain
Cartesian Coordinates ( )zuyuxu === 321 ,,
Linearized Flow Equations
Return to Table of Content

219. 219
SOLO
Cylindrical Coordinates ( )θ=== 321 ,, uruxu
→→→→→→
++=++= zryrxxzzyyxxR 1sin1cos1111 θθ

→→→→→
+−=
∂
∂
+=
∂
∂
=
∂
∂
zryr
R
zy
r
R
x
x
R
1cos1sin&1sin1cos&1 θθ
θ
θθ

r
R
h
r
R
h
x
R
h =
∂
∂
==
∂
∂
==
∂
∂
=
θ

:&1:&1: 321
→→→→
→→→→→→
=+−=
∂
∂
∂
∂
=
=+=
∂
∂
∂
∂
==
∂
∂
∂
∂
=
θθθ
θ
θ
θθ
11cos1sin:
&11sin1cos:&1:
2
21
zy
R
R
e
rzy
r
R
r
R
ex
x
R
x
R
e






1
0
332211
323121
=⋅=⋅=⋅
=⋅=⋅=⋅
→→→→→→
→→→→→→
eeeeee
eeeeee
We have
Linearized Flow Equations

220. 220
SOLO
Cylindrical Coordinates (continue – 1) ( )θ=== 321 ,, uruxu
→→→→→→
Φ+Φ+Φ=
∂
Φ∂
+
∂
Φ∂
+
∂
Φ∂
=Φ∇ 321321
11
e
r
eee
r
e
r
e
x
rx θ
θ
2
2
22 1
θΦ+Φ+Φ=Φ∇⋅Φ∇
r
rx
→
→→






ΦΦ+ΦΦ+ΦΦ+






Φ−ΦΦ+ΦΦ+ΦΦ+





ΦΦ+ΦΦ+ΦΦ=






Φ+Φ+Φ∇=





Φ∇⋅Φ∇∇
322
2
2
3212
2
2
22
11
111
1
2
1
2
1
e
rr
e
rr
e
r
r
rrxx
rrrrxrxxrxrxxx
rx
θθθθθ
θθθθθ
θ
θθ
θ
θθ
Φ+Φ+Φ+Φ=
∂
Φ∂
+
∂
Φ∂
+
∂
Φ∂
+
∂
Φ∂
=












∂
Φ∂
∂
∂
+





∂
Φ∂
∂
∂
+





∂
Φ∂
∂
∂
=
=Φ∇⋅∇=Φ∇
22
2
22
2
2
2
2
1111
11
rrrrrrx
rr
r
rx
r
xr
rrrxx
Linearized Flow Equations

221. 221
SOLO
Cylindrical Coordinates (continue – 2) ( )θ=== 321 ,, uruxu
Then equation 











Φ∇⋅Φ∇∇⋅Φ∇+Φ∇
∂
∂
⋅Φ∇+
∂
Φ∂
=Φ∇⋅∇
2
1
2
1
2
2
2
tta
becomes
( ){












ΦΦ+ΦΦ+ΦΦ+






Φ−ΦΦ+ΦΦ+ΦΦ+









ΦΦ+ΦΦ+ΦΦ





Φ+Φ+Φ+
ΦΦ+ΦΦ+ΦΦ+Φ=Φ+Φ+Φ+Φ
→
→
→→→→
322
2
2
32
12321
22
11
11
11
2
111
e
rr
e
rr
e
r
e
r
ee
arr
rrxx
rrrrxrx
xrxrxxxrx
ztzytyxtxttrrrxx
θθθθθ
θθθ
θθθ
θθ
or
( ) 0
2
112
/
1
1/
1
1
11
22
222
2
22
2
22
22
2
2
2
=ΦΦ+ΦΦ+ΦΦ−
Φ
−






ΦΦΦ+ΦΦΦ+ΦΦΦ−







 Φ
+Φ+Φ






 Φ
−+Φ






 Φ
−+Φ






 Φ
−
ztzytyxtx
tt
rrxxrxrx
rrr
r
xx
x
aa
rra
a
r
ra
r
raa
θθθθ
θ
θθ
θ
Linearized Flow Equations

222. 222
SOLO
Cylindrical Coordinates (continue – 3) ( )θ=== 321 ,, uruxu
becomes
( ) ( ) ( )





Ψ−Ψ+−Φ∇⋅Φ∇+
∂
Φ∂
−−= ∞∞∞
222
2
1
1 u
t
aa γ
In cylindrical coordinates, equation
( ) ( )





Ψ−Ψ+





−Φ+Φ+Φ+Φ−−= ∞∞∞
22
2
2222 1
2
1
1 U
r
aa rxt θγ
Assuming a stationary flow and neglecting body forces





=
∂
∂
0
t
( )0=Ψ
0
112
/
1
1/
1
1
11
222
2
22
2
22
22
2
2
2
=





ΦΦΦ+ΦΦΦ+ΦΦΦ−







 Φ
+Φ+Φ






 Φ
−+Φ






 Φ
−+Φ






 Φ
−
rrxxrxrx
rrr
r
xx
x
rra
a
r
ra
r
raa
θθθθ
θ
θθ
θ
( )






−Φ+Φ+Φ
−
−= ∞∞
22
2
2222 1
2
1
U
r
aa rx θ
γ
Linearized Flow Equations
Return to Table of Content

223. 223
Linearized Flow EquationsSOLO
Boundary Conditions
1. Since the Small Perturbations are not
considering the Boundary Layer the
Flow must be parallel at the Wing
Surface.
The Wing Surface S is defined by
zU (x,y) – Upper Surface
zL (x,y) – Lower Surface
0

=⋅ S
un
n

- Normal at the Wing Surface
22
1/111 





∂
∂
+





∂
∂
+





+
∂
∂
−
∂
∂
−=
y
z
x
z
zy
y
z
x
x
z
n UUUU
U

( ) ( ) ( ) ( ) zwUyvxuUzwUyvxuUu 1'1'1'1'sin1'1'cos ++++≅++++= ∞∞∞∞ ααα

( ) ( ) 0,,''' =++
∂
∂
−
∂
∂
+− ∞∞ U
UU
zyxwU
x
z
v
x
z
uU α
For Upper Surface
( ) ( ) 





−
∂
∂
≅
∂
∂
+
∂
∂
+= ∞∞ α
x
z
U
x
z
v
x
z
uUzyxw U
onPerturbati
Small
UU
U '',,'
Therefore
( )
( )
( ) Sonyxallfor
x
z
Uzyxw
x
z
Uzyxw
L
L
U
U
,
,,'
,,'













−
∂
∂
≅






−
∂
∂
≅
∞
∞
α
α
Section AA
(enlarged)
Wake region

224. 224
Linearized Flow EquationsSOLO
Boundary Conditions (continue -1)
1. Flow must be parallel at the Wing Surface.
The Wing Surface S is defined by
zU (x,y) – Upper Surface
zL (x,y) – Lower Surface
Since the Small Perturbation gives
Linear Equation we can divide the
Airfoil in the Camber Distribution zC (x,y)
and the Thickness Distribution zt (x,y) by:
( )
( )
( ) Sonyxallfor
x
z
Uyxw
x
z
Uyxw
C
C
t
t
,
0,,'
0,,'













−
∂
∂
=
∂
∂
±=±
∞
∞
α
( ) ( ) ( )
( ) ( ) ( )
( ) ( ) ( )[ ]
( ) ( ) ( )[ ]


−=
+=
⇔



−=
+=
2/,,,
2/,,,
,,,
,,,
yxzyxzyxz
yxzyxzyxz
yxzyxzyxz
yxzyxzyxz
LUt
LUC
tCL
tCU
Because of the Linearity the complete solution can be obtained by summing the
Solutions for the following Boundary Conditions
Superposition of
• Angle of Attack
•Camber Distribution
•Thickness Distribution
Section AA
(enlarged)
Wake region
( ) ( ) ( )
( ) ( ) ( )
( ) Sonyxallfor
x
z
x
z
Uyxwyxwyxw
x
z
x
z
Uyxwyxwyxw
tC
tCL
tC
tCU
,
0,,'0,,'0,,'
0,,'0,,'0,,'













∂
∂
−−
∂
∂
=−+=±






∂
∂
+−
∂
∂
=++=±
∞
∞
α
α

225. 225
Linearized Flow EquationsSOLO
Boundary Conditions (continue -2)
2. Disturbances Produced by the Motion
must Die Out in all portion of the Field
remote from the Wing and its Wake
Normally this requirement is met by making
ϕ→0 when y→ ±0, z → ±0, x→-∞
Subsonic Leading
Edge Flow
Subsonic Trailing
Edge Flow
Supersonic Leading
Edge Flow
Supersonic Trailing
Edge Flow
3. Kutta Condition at the Trailing Edge of a
Steady Subsonic Flow
There cannot be an infinite change in velocity at the
Trailing Edge. If the Trailing Edge has a non-zero
angle, the flow velocity there must be zero. At a cusped
Trailing Edge, however, the velocity can be non-zero
although it must still be identical above and below the
airfoil. Another formulation is that the pressure must
be continuous at the Trailing Edge.
http://nylander.wordpress.com/category/engineering/
Kutta Condition does not apply to Supersonic
Flow since the shape and location of the
Trailing Edge exert no influence on the flow
ahead.

226. 226
SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
'2u
∞+Uu '1∞U
( )
( )
'
'
'2'
'
'0
''2'0
'
222
1
33
2
11
22
22
11
ρρρ
φ
+=
+=
+≈+=
+=Φ
+=
++=+=
+=
∞
∞
∞∞∞
∞
∞∞
∞
ppp
aaaaaa
xU
uu
uuUUuuu
uUu
O
Small Perturbation Assumptions:












∇⋅+
∂
∂
⋅+
∂
Φ∂
=⋅∇
2
2
1 2
2
2
2
u
u
t
u
u
ta
u



(C.M.) +(C.L.M)
(C.M.) +(C.L.M)
12
1
12
1
2
2
2
2
−
+=
−
++
∂
∂ ∞
∞
γγ
φ a
U
a
u
t
Bernoulli
121 −
∞
−
∞∞∞






=





=





=
γ
γ
γ
γ
γ
ρ
ρ
a
a
T
T
p
p
Isentropic Chain
Development of the Flow Equations:
Flow Equations:
( ) '' 2
1 φφ ∇=+∇⋅∇=⋅∇ ∞ xUu

( )
1
1
2
2
1
12
12
2
2
''
'
1
2
1
x
u
a
U
x
u
uU
a
u
u
a ∂
∂
≅+
∂
∂
+≅





∇⋅
∞
∞
∞
∞


( ) t
u
UuUU
tt
u
t
u
u
∂
∂
=+
∂
∂
≅
∂
∂
=
∂
∂
⋅ ∞∞∞
'
2'22 1
1
2
2

( )

∞
∞
∞
∞
∞
∞
∞∞
∞∞ ++
∂
∂
=⇒
−
+=
−
+
+++
∂
∂
ρ
γ
φ
γγ
φ
p
a
puU
t
a
U
aaa
uUU
t
2
1
2
2
2
1
2
''
'
0
12
1
1
'2
'2
2
1'
∞∞∞∞∞∞∞∞ −
=
−
==⇒
−
=
−
==
a
a
T
T
p
p
a
ad
T
Tdd
p
pd '
1
2'
1
''
1
2
1 γ
γ
γ
γ
ρ
ρ
γ
γ
γ
γ
γ
ρ
ρ
γ Isentropic Chain
Bernoulli
Linearized Flow Equations

227. 227
SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
'2u
∞+Uu '1∞U
Small Perturbation Flow Equations:
(C.M.) +(C.L.M) 52.1&8.00
''
2
'1
' 2
2
1
1
12
2
2
≤≤≤≤





∂
∂
+
∂
∂
+
∂
∂
=∇ ∞∞
∞
MM
tt
u
U
x
u
U
a
φ
φ
( )
''
,,,'' 321
φ
φφ
∇=
=
u
xxxt

Bernoulli 





+
∂
∂
−= ∞∞ '
'
' 1uU
t
p
φ
ρ
∞∞∞∞ −
=
−
==
a
a
T
T
p
p '
1
2'
1
''
γ
γ
γ
γ
ρ
ρ
γIsentropic Chain
Linearized Flow Equations

228. 228
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Three Dimensional Flow (Thin Wings at Small Angles of Attack)
α
U
Up
xd
ud
θ=
L
Low
xd
ud
θ−=
∞U
x
z
( ) 0
'''
1 2
2
2
2
2
2
2
=
∂
∂
+
∂
∂
+
∂
∂
− ∞
zyx
M
φφφ
(1)
( )zyx ,,'φ(2)
z
w
y
v
x
u
∂
∂
=
∂
∂
=
∂
∂
=
'
',
'
',
'
'
φφφ
(3)
α−=≅
+ ∞∞ S
xd
zd
U
w
uU
w '
'
'
(4)
x
UuUp
∂
∂
−=−= ∞∞∞∞
'
''
φ
ρρ(5)
'
2
1
1
''
1
2'
1
''
2
M
M
M
U
u
M
a
a
T
T
p
p
∞
∞
∞
∞
∞∞∞∞
−
+
−=−=
−
=
−
==
γ
γ
γ
γ
γ
γ
γ
ρ
ρ
γ(6)








∂
∂
+
∂∂
∂
+
∂
∂
=∇
∞∞∞
2
2
2
2
2
2
2
2 '1'2'1
'
tUxtUxM
φφφ
φ
( )
''
,,,''
φ
φφ
∇=
=
u
zyxt







+
∂
∂
−= ∞∞ '
'
' uU
t
p
φ
ρ
Steady Three Dimensional Flow Small Perturbation Flow Equations:
0
'
2
2
=
∂
∂
=
∂
∂
tt
52.1
8.00
≤≤
≤≤
∞
∞
M
M

229. 229
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Three Dimensional Flow (Thin Wings at Small Angles of Attack)
0
'''
2
2
2
2
2
2
2
=
∂
∂
+
∂
∂
+
∂
∂
zyx
φφφ
β(1)
Steady Three Dimensional Flow
Subsonic Flow M∞ < 1
01:
22
>−= ∞Mβ
( )
( )
( )
( )
α
ξ
α
φ
α
ξ
α
φ
−=−=
∂
∂
=
−=−=
∂
∂
=
∞∞
∞∞
LowerLower
Lower
UperUper
Upper
d
zd
xd
zd
zUU
w
d
zd
xd
zd
zUU
w
'1'
'1'
3
4
3
4
Transform of Coordinates
( ) ( )






=
=
=
=−= ∞
ςηξφφ
ς
η
ξβξ
,,,,'
1 2
zyx
z
y
Mx










∂
∂
=
∂
∂
⇒
∂
∂
=
∂
∂
∂
∂
=
∂
∂
⇒
∂
∂
=
∂
∂
∂
∂
=
∂
∂
⇒
∂
∂
=
∂
∂
2
2
2
2
2
2
2
2
2
2
22
2
''
''
1'1'
ς
φφ
ς
φφ
η
φφ
η
φφ
ξ
φ
β
φ
ξ
φ
β
φ
zz
yy
xx
( ) ( ) SMdcMydycS
bb
∞∞
−=−== ∫∫ 2
0
2
0
11 ηη
( ) ( )ηcMyc 2
1 ∞−=
∞∞
−
=
−
==
22
22
11 M
AR
SM
b
S
b
AR
22
1
2
1
12
∞∞∞∞ −
=
∂
∂
−
−=
∂
∂
−=
M
C
UMxU
C
p
p
ξ
φφ
Section AA
(enlarged)
Wake region
so 02
2
2
2
2
2
=
∂
∂
+
∂
∂
+
∂
∂
ς
φ
η
φ
ξ
φ
Laplace’s Equation like in Incompressible Flow
Similarity Rules

230. 230
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Three Dimensional Flow (Thin Airfoil at Small Angles of Attack)
incpC
M 2
1
1
∞−
incLC
M 2
1
1
∞−
22
1
2
1
1
∞∞ −
=





− Md
Cd
M inc
L α
α
incMC
M 2
1
1
∞−
inc0α
4
1
=





inc
N
c
x
incMC
M
02
1
1
∞−
incLsC
M 2
1
1
∞−
incsα
LsC
sα
0MC
c
xN
MC
0α
αd
Cd L
LC
pCPressure Distribution
Lift
Lift Slope
Zero-Lift Angle
Pitching Moment
Neutral-Point Position
Zero Moment
Angle of Smooth
Leading-Edge Flow
Lift Coefficient of Smooth
Leading-Edge Flow
Aerodynamic Coefficients of a Profile in Subsonic Incident Flow
Based on Subsonic Similarity Rules

231. 231
SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
α
U
Up
xd
ud
θ=
L
Low
xd
ud
θ−=
∞U
x
y
( ) 0
''
1 2
2
2
2
2
=
∂
∂
+
∂
∂
− ∞
yx
M
φφ(1)
( )yx,'φ(2)
y
v
x
u
∂
∂
=
∂
∂
=
'
',
'
'
φφ
(3)
α==≅
+ ∞∞ S
xd
yd
U
v
vU
v '
'
'
(4)
x
UuUp
∂
∂
−=−= ∞∞∞∞
'
''
φ
ρρ(5)
'
2
1
1
''
1
2'
1
''
2
M
M
M
U
u
M
a
a
T
T
p
p
∞
∞
∞
∞
∞∞∞∞
−
+
−=−=
−
=
−
==
γ
γ
γ
γ
γ
γ
γ
ρ
ρ
γ(6)






∂
∂
+
∂
∂
+
∂
∂
=∇ ∞∞
∞
2
2
1
1
12
2
2 ''
2
'1
'
tt
u
U
x
u
U
a
φ
φ
( )
''
,,,'' 321
φ
φφ
∇=
=
u
xxxt







+
∂
∂
−= ∞∞ '
'
' uU
t
p
φ
ρ
Steady Two Dimensional Flow Small Perturbation Flow Equations:
0
'
2
2
=
∂
∂
=
∂
∂
tt
52.1
8.00
≤≤
≤≤
M
M
Linearized Flow Equations

232. 232
SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
0
''
2
2
2
2
2
=
∂
∂
+
∂
∂
yx
φφ
β(1)
Steady Two Dimensional Flow
Subsonic Flow M∞ < 1
01:
22
>−= ∞Mβ
( )
( )
( )
( )
α
φ
α
φ
−=
∂
∂
=
−=
∂
∂
=
∞∞
∞∞
Lower
Lower
Uper
Upper
xd
yd
yUU
v
xd
yd
yUU
v
'1'
'1'
3
4
3
4
∞U
α
Transform of Coordinates
( ) ( )




=
=
=
yx
y
x
,', φβηξφ
βη
ξ











∂
∂
=
∂
∂
∂
∂
=
∂
∂
∂
∂
=





∂
∂
∂
∂
+
∂
∂
∂
∂
=
∂
∂
=
∂
∂
∂
∂
=





∂
∂
∂
∂
+
∂
∂
∂
∂
=
∂
∂
=
∂
∂
2
2
2
2
2
2
2
2
'
,
1'
11'
111'
η
φφ
ξ
φ
β
φ
η
φη
η
φξ
ξ
φ
β
φ
β
φ
ξ
φ
β
η
η
φξ
ξ
φ
β
φ
β
φ
yx
yyyy
xxxx
so 02
2
2
2
=
∂
∂
+
∂
∂
η
φ
ξ
φ
Laplace’s Equation like in Incompressible Flow
Linearized Flow Equations

233. 233
SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Steady Two Dimensional Flow
Subsonic Flow M∞ < 1 (continue)
The Airfoil is defined in (x,y) plane and by (ξ,η)
( ) ( )ξη gxfy AirfoilAirfoil =⇔=
The above Transformation relates the
Compressible Flow over an Airfoil
in (x,y) Space to the Incompressible Flow
in (ξ,η) over the same Airfoil.
α
η
φφ
−=
∂
∂
=
∂
∂
=
∞∞∞ Uper
Upper
xd
yd
UyUU
v 1'1'
α
η
φφ
−=
∂
∂
=
∂
∂
=
∞∞∞ Lower
Lower
xd
yd
UyUU
v 1'1'
( )yx,ρρ =
x
y η
ξ
∞= ρρ
Compressible Flow Incompressible Flow
α
η
φ
−=
∂
∂
=
∞∞ Uper
Upper
xd
fd
UU
v 1'
α
η
φ
−=
∂
∂
=
∞∞ Lower
Lower
xd
fd
UU
v 1'
Linearized Flow Equations

234. 234
SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
0
'1'
2
2
22
2
=
∂
∂
−
∂
∂
yx
φ
β
φ
(1)
( ) ( ) ( )
( ) ( ) ( ) yxGyxGyx
yxFyxFyx
Lower
Upper
βννβφ
βηηβφ
+==+=
−==−=
:,'
:,'(7)
(8)
Steady Two Dimensional Flow
Supersonic Flow M∞ > 1
01:
22
>−= ∞Mβ
α
U
Up
xd
yd
θ=
L
Low
xd
yd
θ−=
∞U
x
y
1
1
2
−
=
∞Mxd
yd
1
1
2
−
−=
∞Mxd
yd
Flow
Flow
( )
( )
( )
η
β
α
d
Fd
Uxd
yd
U
v
Uper
Upper
∞∞
−=−=
1
7
4'
( ) ( )
η
φ
d
Fd
xd
d
u Upper
73
'
' ==








−
−
−=
∞
∞
α
Upper
Upper
xd
yd
M
U
u
1
'
2
( )
( )
( )
ν
β
α
d
Gd
Uxd
yd
U
v
Lower
Lower
∞∞
=−=
3
8
4
'
( ) ( )
ν
φ
d
Gd
xd
d
u Lower
83
'
' ==








−
−
=
∞
∞
α
Lower
Lower
xd
yd
M
U
u
1
'
2








−
−
=−=
∞
∞∞
∞∞ α
ρ
ρ
Upper
UpperUpper
xd
yd
M
U
uUp
1
''
2
2








−
−
−=−=
∞
∞∞
∞∞ α
ρ
ρ
Lower
LowerLower
xd
yd
M
U
uUp
1
''
2
2
Linearized Flow Equations

235. 235
SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Drag (D) and Lift (L) Computations
( )∫ 







−−= ∞
S S
sd
xd
yd
ppD αsin
np
α−
Upper
xd
yd
∞U
Upper
xd
yd
∞p∞p α( )∫ 







−−−= ∞
S S
sd
xd
yd
ppL αcos
( )∫ 







−−≅ ∞
S S
sd
xd
yd
ppD α
( )

Γ
∞∞∞ ∫∫ =








−−−≅
SS S
sduUsd
xd
yd
ppL 'ρα
1<<−α
Uper
xd
yd
1<<−α
Uper
xd
yd
Kutta-Joukovsky
Define: 2
2
1
:
∞∞
∞−
=
U
pp
Cp
ρ
( )
( )
∫∫
∫∫








−−=








−
−
−≅








−=








−
−
≅
∞∞
∞∞
∞
∞∞
∞∞
∞∞
∞
∞∞
S S
p
S S
S S
p
S S
sd
xd
yd
CUsd
xd
yd
U
pp
UL
sd
xd
yd
CUsd
xd
yd
U
pp
UD
αρα
ρ
ρ
αρα
ρ
ρ
2
2
2
2
2
2
2
1
2
12
1
2
1
2
12
1
Linearized Flow Equations

236. 236
SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Drag (D) and Lift (L) Computations for Subsonic Flow (M∞ < 1)
np
α−
Upper
xd
yd
∞U
Upper
xd
yd
∞p∞p α
We found:
α−=
∞ xd
fd
U
v'
α
ξ
−=
∞ d
gd
U
v
( ) ( )











−=
−=
=
∞
∞
yxM
yM
x
,'1,
1
2
2
φηξφ
η
ξ
( ) 0
''
1 2
2
2
2
2
=
∂
∂
+
∂
∂
− ∞
yx
M
φφ 02
2
2
2
=
∂
∂
+
∂
∂
η
φ
ξ
φ
y
v
x
u
∂
∂
=
∂
∂
=
'
',
'
'
φφ
η
φ
ξ
φ
∂
∂
=
∂
∂
= vu ,
vv
M
u
u =
−
=
∞
',
1
'
2
'' uUp ∞∞−= ρ uUp ∞∞−= ρ
xUU
u
U
pp
Cp
∂
∂
−=−=
−
=
∞∞
∞∞
∞ '2'2
2
1
'
:
2
φ
ρ ξ
φ
ρ ∂
∂
−=−=
−
=
∞∞
∞∞
∞
UU
u
U
pp
Cp
22
2
1
:
2
0
2
1
'
∞−
=
M
p
p
2
1
0
∞−
=
M
C
C
p
p
Compressible: Incompressible:
Linearized Flow Equations

237. 237
SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Drag (D) and Lift (L) Computations for Subsonic Flow (M∞ < 1)
np
α−
Upper
xd
yd
∞U
Upper
xd
yd
∞p∞p α
The Relation:
∫∫
∫∫






−
−=













−−≅














−
−
=













−≅
∞
∞∞
∞∞
∞
∞∞
∞∞
S
p
S S
p
S S
p
S S
p
c
s
dC
M
U
c
s
d
xd
yd
CUL
c
s
d
xd
yd
C
M
U
c
s
d
xd
yd
CUD
0
0
2
2
2
2
2
2
1
2
1
2
1
1
2
1
2
1
ρ
αρ
α
ρ
αρ
2
1
0
∞−
=
M
C
C
p
p
Prandtl-Glauert
Compressibility Correction
As earlier in 1922, Prandtl is quoted as stating that the Lift
Coefficient increased according to (1-M∞
2
)-1/2
; he mentioned
this at a Lecture at Göttingen, but without a proof. This result was
mentioned 6 years later by Jacob Ackeret, again without proof.
The result was finally established by H. Glauert in 1928 based on
Linear Small Perturbation.
Ludwig Prandtl
(1875 – 1953)
Hermann Glauert
(1892-1934)
Linearized Flow Equations
Return to
Critical Mach Number

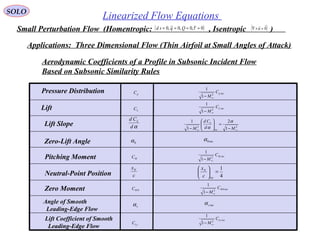
238. SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Several improved formulas where developed:
( )[ ] 2/11/1 0
0
222
p
p
p
CMMM
C
C
∞∞∞ −++−
= Karman-Tsien
Rule
Linearized Flow Equations
( ) 0
0
2222
12/
2
1
11 p
p
p
CMMMM
C
C






−




 −
++−
=
∞∞∞∞
γ
Laitone’s
Rule
Comparison of several compressibility corrections
compared with experimental results for NACA 4412
Airfoil at an angle of attack of α = 1◦
.
Return to Table of Content

239. 239
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
0
'1'
2
2
22
2
=
∂
∂
−
∂
∂
zx
φ
β
φ
(1)
( ) ( ) ( )
( ) ( ) ( ) zxFzxGzx
zxFzxFzx
Lower
Upper
βννβφ
βηηβφ
+==+=
−==−=
:,'
:,'(7)
(8)
Steady Two Dimensional Flow
Supersonic Flow M∞ > 1
01:
22
>−= ∞Mβ
α
U
Up
xd
zd
θ=
L
Low
xd
zd
θ−=
∞U
x
z
1
1
2
−
=
∞Mxd
zd
1
1
2
−
−=
∞Mxd
zd
Flow
Flow
( )
( )
( )
η
β
α
d
Fd
Uxd
zd
U
w
Upper
Upper
∞∞
−=−=
3
7
4'
( ) ( )
η
φ
d
Fd
xd
d
u Upper
73
'
' ==
( )
( )
( )
ν
β
α
d
Gd
Uxd
zd
U
w
Lower
Lower
∞∞
==−=
3
8
4
'
( ) ( )
ν
φ
d
Gd
xd
d
u Lower
83
'
' ==








−
−
−=
∞
∞
α
Upper
Upper
xd
zd
M
U
w
1
'
2








−
−
=
∞
∞
α
Lower
Lower
xd
zd
M
U
w
1
'
2








−
−
=−==−
∞
∞∞
∞∞∞ α
ρ
ρ
Upper
UpperUpperUpper
xd
zd
M
U
wUppp
1
''
2
2








−
−
−=−==−
∞
∞∞
∞∞∞ α
ρ
ρ
Lower
LowerLowerLower
xd
zd
M
U
wUppp
1
''
2
2
z
w
x
u
∂
∂
=
∂
∂
=
'
',
'
'
φφ
(3)
α−=≅
+ ∞∞ S
xd
zd
U
w
uU
w '
'
'
(4)

240. 240
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Steady Two Dimensional Flow
Supersonic Flow M∞ > 1
α
U
Up
xd
zd
θ=
L
Low
xd
zd
θ−=
∞U
x
z
1
1
2
−
=
∞Mxd
zd
1
1
2
−
−=
∞Mxd
zd
Flow
Flow
Pressure Distribution and Lift Coefficient








−+
−
=
−
=
∞∞∞
α
ρ
2
1
2
2/
''
22
LowerUpper
LowerUpper
p
xd
zd
xd
zd
MU
pp
C
1
4
2
−
=
∞M
cL
α
( ) ( ) ( ) ( )








−+−
−
−
−
=








+





−





−
−
=





+





−=
∞∞
∞
∫∫∫∫
    
00
22
1
0
1
02
1
0
1
0
00
1
2
1
4
2
1
2
LowerLowerUpperUpper
LowerUpper
ppL
zczzcz
MM
c
x
d
xd
zd
c
x
d
xd
zd
Mc
x
dC
c
x
dCc LowerUpper
α
α








−
−
=
∞
α
Upper
p
xd
zd
M
C Upper
1
2
2 







−
−
−=
∞
α
Lower
p
xd
zd
M
C Lower
1
2
2

241. 241
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Steady Two Dimensional Flow
Supersonic Flow M∞ > 1
α
U
Up
xd
zd
θ=
L
Low
xd
zd
θ−=
∞U
x
z
1
1
2
−
=
∞Mxd
zd
1
1
2
−
−=
∞Mxd
zd
Flow
Flow
Wave Drag Coefficient
























−+













−
−
=













−−













−= ∫∫∫∫
∞
1
0
2
1
0
2
2
1
0
1
0
1
2
c
x
d
xd
zd
c
x
d
xd
zd
Mc
x
d
xd
zd
C
c
x
d
xd
zd
Cc
UpperUpperLower
p
Upper
pD LowerUpperW
αααα








−
−
=
∞
α
Upper
p
xd
zd
M
C Upper
1
2
2 







−
−
−=
∞
α
Lower
p
xd
zd
M
C Lower
1
2
2
( ) ( ) ( ) ( ) 



























+





−+













+





−
−
= ∫∫∫∫
=−=−
∞
1
0
2
00
1
0
2
1
0
2
00
1
0
2
2
22
1
2
c
x
d
xd
zd
c
x
d
xd
zd
c
x
d
xd
zd
c
x
d
xd
zd
M Lower
zcz
LowerUpper
zcz
Upper
LowerLowerUpperUpper
    
αααα
( )22
22
2
1
2
1
4
LowerUpperD
MM
C W
εε
α
+
−
+
−
=
∞∞
∫
∫














=














=
1
0
2
2
1
0
2
2
:
:
c
x
d
xd
zd
c
x
d
xd
zd
Lower
Lower
Upper
Upper
ε
ε

242. 242
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Steady Two Dimensional Flow
Supersonic Flow M∞ > 1
Wave Drag Coefficient
Flat Plate 







== 0
LowerUpper
xd
zd
xd
zd
Double Wedge Airfoil
1
4
2
2
−
=
∞M
C WD
α
022
== LowerUpper εε
( )
( )
( )kkc
t
ck
c
t
k
ck
c
t
kc
LowerUpper
−
=






−
−
+==
14
1
1
14
1
4
11
2
2
2
2
22
2
2
22
εε
( ) ( )






<<
−
<<−
=







<<
−
−
<<
=
cxck
ck
t
ckx
ck
t
xd
zd
cxck
ck
t
ckx
ck
t
xd
zd
LowerUpper
12
0
2
12
0
2
( )
( )kk
ct
MM
C WD
−−
+
−
=
∞∞
1
/
1
1
1
4
2
22
2
α

243. 243
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Steady Two Dimensional Flow
Supersonic Flow M∞ > 1
Wave Drag Coefficient
Biconvex Airfoil
( ) ( )222
2/2/ ctRR +−=
The Biconvex Airfoil is obtained by intersection of two
Circular Arcs of radius R.
c – the chord
t – maximum thickness at x = c/2
( ) ( ) ( )tcttcR
tc
4/4/ 222
22
>>
≈+=
θθθθ −≈−=≈= tan,tan
LowerUpper
xd
zd
xd
zd
2
2
2/2
/2
3
2
1
0
2
1
0
2
2
3
2
34
11
: Lower
ct
ctUpperUpper
Upper
c
t
t
c
dR
c
xd
xd
zd
cc
x
d
xd
zd
ε
θ
θθε
δ
δ
==≈≈








=













=
+
−
+
−∫∫∫
c
t
R
c
xd
zd
MaxUpper
2
2/
, ≈≈≈








δδ
( ) 2
2
22
2
22
22
2
3
16
1
1
1
4
1
2
1
4
c
t
MMMM
C LowerUpperDW
−
+
−
=+
−
+
−
=
∞∞∞∞
α
εε
α

244. 02/04/15 244
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Steady Two Dimensional Flow
Supersonic Flow M∞ > 1
Wave Drag Coefficient
Parabolic ProfileDesignation Double Wedge Profile
Contour
Side View
Wave Drag
( )kk −13
1
2( )kk −1
1
( )
( ) xckck
xcxt
z
212 22
−+
−
±=
( )






<<
−
±
<<±
=
cxckx
ck
t
ckxx
ck
t
z
12
0
2

245. 245
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Steady Two Dimensional Flow
Supersonic Flow M∞ > 1
Wave Drag Coefficient
Wave Drag at Supersonic Incident Flow
versus Relative Thickness Position
for Double Wedge and Parabolic Profiles
k
( )kk −1
1
( )kk −13
1
2

246. 246
SOLO Wings in Compressible Flow
Double Wedge
Modified Double Wedge
Biconvex
τ
2
1
2
122
1
2
' 2
==






=
c
t
c
t
c
A
τ
3
2
3
2332
1
2
' 2
==
+





=
c
t
c
t
c
t
c
A

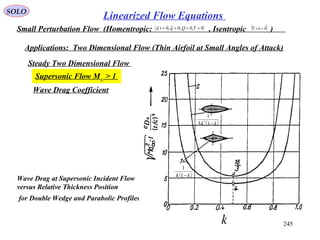
247. 247
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Steady Two Dimensional Flow
Supersonic Flow M∞ > 1
Pitching Moment Coefficient
The Pitching Moment Coefficient about the
Leading Edge for any Thin Airfoil is given by
xdx
xd
zd
xd
zd
Mcc
x
d
c
x
C
c
x
d
c
x
Cc
c
LowerUpper
ppM LowerUpperLE ∫∫∫ 















−+








−
−
−=











+











−=−
∞
022
1
0
1
0
1
2
αα
Thus




 +
−
+
−
−= ∫∫
∞∞
xdzxdz
McM
c
c
Lower
c
UpperM LE 00222
1
2
1
2α
( ) ( ) ( ) ( )[ ] xdzxdzczczcxdzzxxdzzxxdx
xd
zd
xd
zd c
Lower
c
UpperLowerUpper
c
Lower
cx
xLower
c
Upper
cx
xUpper
c
LowerUpper
∫∫∫∫∫ −−−=−+−=








+
=
=
=
= 00
0
00000   
Using integration by parts
Symmetric Airfoil zUpper = -zLower
1
2
2
−
−=
∞M
cM
α
The distance of the Airfoil Center of Pressure aft of the Leading Edge is given by
cc
M
M
c
c
c
c
x
L
MN
2
1
1/4
1/2
2
2
=⋅
−
−
=⋅−=
∞
∞
α
α
α
L
∞U
x
Return to Table of Content

248. 248
SOLO
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Drag (D) and Lift (L) Computations for Supersonic Flow (M∞ >1)






















−+








−
−
−=





−≅






















−+








−
−
=













−≅
∫∫
∫∫
∞
∞∞
∞∞
∞
∞∞
∞∞
c
x
d
xd
yd
xd
yd
M
U
c
s
dCUL
c
x
d
xd
yd
xd
yd
M
U
c
s
d
xd
yd
CUD
c
LowerUpperS
p
c
LowerUpperS S
p
0
2
2
2
0
22
2
2
2
2
1
2
1
2
1
2
1
2
1
2
1
αα
ρ
ρ
αα
ρ
αρ
α
U
Up
xd
yd
θ=
L
Low
xd
yd
θ−=
∞U
x
y
1
1
2
−
=
∞Mxd
yd
1
1
2
−
−=
∞Mxd
yd
Flow
Flow








−
−
==−
∞
∞∞
∞ α
ρ
Upper
UpperUpper
xd
yd
M
U
ppp
1
'
2
2








−
−
−==−
∞
∞∞
∞ α
ρ
Lower
LowerLower
xd
yd
M
U
ppp
1
'
2
2
1
2
1
2
2
2
−








−
−=
−








−
=
∞
∞
M
xd
yd
C
M
xd
yd
C
Lower
p
Upper
p
Lower
Upper
α
α
We found:
This relation was first derived by Jacob Ackeret in 1925, in a paper
“Luftkrafte auf Flugel, die mit groserer als Schall-geschwingigkeit bewegt werden”
(“Air Forces on Wings Moving at Supersonic Speeds”), that appeared in
Zeitschhrift fur Flugtechnik und Motorluftschiffahrt, vol. 16, 1925, p.72
Jakob Ackeret
(1898–1981)
Linearized Flow Equations

249. 249
AERODYNAMICS
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Drag (D) and Lift (L) Computations for Supersonic Flow (M∞ >1)
Supersonic Flow past a Symmetric Double-Edged Airfoil
1
2
3
4
SHOCK LINE
SHOCK LINE
SHOCK LINE
SHOCK LINE
EXPANSION
EXPANSION
Using Ackeret Theory we have
( ) ( )
( ) ( )
1
2
,
1
2
1
2
,
1
2
22
22
43
21
−
−
−=
−
+
−=
−
+
=
−
−
=
∞∞
∞∞
M
C
M
C
M
C
M
C
pp
pp
αδαδ
αδαδ
( ) ( )
1
4
2
1
1
4
2
1
1
4
222
1
2/1
2/1
0 3412
−
=
−
+
−
=






−+





−=





=
∞∞∞
∫∫∫
MMM
c
x
dCC
c
x
dCC
c
s
dCC pppp
S
pX
ααα
( ) ( )
( ) ( )
1
4
1
4
2
2
22 2
2/
2
0
2/
2/
0
3412
3412
−
=
−
×=−+−=






−+





−=





=
∞
=
∞
−∫∫∫
MMc
t
CC
c
t
CC
c
t
c
y
dCC
c
y
dCC
c
y
dCC
ct
pppp
ct
pp
ct
pp
S
pX
δδ δ
XYXYD
XYXYL
CCCCC
CCCCC
+≈+=
−≈−=
<<
<<
ααα
ααα
α
α
1
1
cossin
sincos
1
4
1
4
1
4
1
4
2
2
2
21
2
2
2
1
−
+
−
≈
−
−
−
≈
∞∞
<<
∞∞
<<
MM
C
MM
C
D
L
δα
αδα
α
α

250. 250
AERODYNAMICS
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Drag (D) and Lift (L) Computations for Supersonic Flow (M∞ >1)

251. 251
pc−
cx /
0.1
pc−
cx /
0.1
pc−
cx /
0.1
α
δα <
δ
∞M
δα >
∞M
∞M
δα =
α
∞M
Upper Surface
Lover Surface
Expansion
Shock
Shock
Expansion
Expansion
Shock
Expansion
Shock
Shock
Expansion
Expansion
Shock
Shock
Shock
Shock
∞M
∞M
( )
1
2
2
−
−
=
∞M
cp
αδ
( )
1
2
2
−
+
=
∞M
cp
αδ
( )
1
2
2
−
−
=
∞M
cp
αδ
( )
1
2
2
−
+
=
∞M
cp
αδ
1
4
2
−
=
∞M
cp
α
1
4
2
−
−
=
∞M
cp
α
( )
1
2
2
−
+
−=
∞M
cp
αδ
( )
1
2
2
−
−
−=
∞M
cp
αδ
( )
1
2
2
−
+
−=
∞M
cp
αδ
( )
1
2
2
−
−
−=
∞M
cp
αδ
Supersonic Flow past a Symmetric Biconvex Aerfoil
AERODYNAMICS
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Two Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Drag (D) and Lift (L) Computations for Supersonic Flow (M∞ >1)
2
2
2
2
2
2
2
4
1
1
3
16
3
16
1
4
LD
L
C
M
M
c
t
C
c
tD
L
Md
Cd
−
+
−






=






+
=
−
=
∞
∞
∞
α
α
α

252. 252
SOLO
Linearized Flow Equations
Small Perturbation Flow (Homentropic: , Isentropic )( )0~,0,0~,0 ==== τQqsd ( )0

=×∇ u
Applications: Three Dimensional Flow (Thin Airfoil at Small Angles of Attack)
Aerodynamic Coefficients of a Profile in Supersonic Incident Flow
Based on the Linear Theory Supersonic Rules






−
−
=
∞
Xd
Zd
M
α
1
1
2
1
4
2
−
=
∞M
2
1
=
0DC
0α
0MC
c
xN
αd
Cd L
pCPressure Distribution
Lift Slope
Neutral-Point Position
Zero Moment
Zero-Lift Angle 0=
( )
∫−
−=
∞
1
02
1
4
XdZ
M
S
Wave Drag
L
D
Cd
Cd 1
4
1 2
−−= ∞M
( ) ( )
∫ 













+





−
−=
∞
1
0
22
2
1
4
Xd
Xd
Zd
Xd
Zd
M
tS

253. 253
SOLO
• Up to point A the flow is Subsonic and it follows Prandtl-
Glauert Linear Subsonic Theory.
• At point B (M∞=0.81) the flow on the Upper Surface exceeds
the Sound Velocity and a Shock Wave occurs. On the Lower
Surface the Flow is everywhere Subsonic.
• At point C (M∞=0.89) the Flow velocity exceeds the Speed of
Sound also on the Lower Surface and a Shock Wave occurs.
• At point D (M∞=0.98) the two Shock Waves on the Upper
and Lower Surface (weaker than at point C) are located at
the Trailing Edge. The Lift is larger than at point C.
• At point E (M∞=1.4) pure Supersonic Flow on both
Surfaces.
Transonic Flow past Airfoils
Lift Coefficient of an Airfoil versus Mach Number.
Solid Line – Measurement. Dashed Lines - Theory
AERODYNAMICS
Transonic Flow over an Airfoil at various
Mach Numbers; Angle of Attack α=2°.
The points A,B, C, D,E correspond to the Lift
Coefficients.

254. 254
AERODYNAMICS
Return to Table of Content

255. 255
Brenda B. Kulfan, “Aerodynamic of Sonic Flight”, Boeing Commercial Airplane
SOLO AERODYNAMICS
Return to Table of Content

256. 256
SOLO
References
Air Breathing Jet Engines
William F. Hughes
“Schaum’s Outline of
Fluid Dynamics”,
McGraw Hill, 1999
Ascher H. Shapiro
“The Dynamics and Thermodynamics
of Compressible Fluid Flow”,
Wiley, 1953
John D. Anderson
“Modern Compressible Flow:
with Historical erspective”,
McGraw-Hill, 1982
John D. Anderson
“Computational Fluid Dynamics”,
1995
Irving Herman Shames
“Mechanics of Fluids”
McGraw-Hill, 4th
Ed,,
2003
D.Pnueli, C. Gutfinger
“Fluid Mechanics”
Cambridge University
Press, 1997
I.H. Abbott, A.E. von Doenhoff
“Theory of Wing Section”, Dover,
1949, 1959
Louis Melveille Milne-Thompson
“Theoretical Aerodynamics”,
Dover, 1988
Return to Table of Content

257. February 4, 2015 257
SOLO
Technion
Israeli Institute of Technology
1964–1968BSc EE
1968–1971MSc EE
Israeli Air Force
1970–1974
RAFAEL
Israeli Armament Development Authority
1974–2013
Stanford University
1983–1986PhD AA 2013-Retired