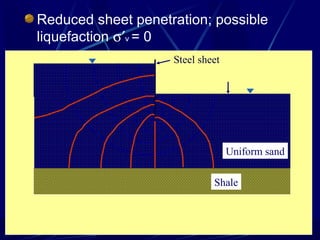
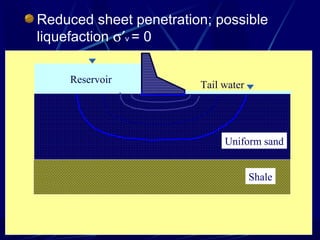
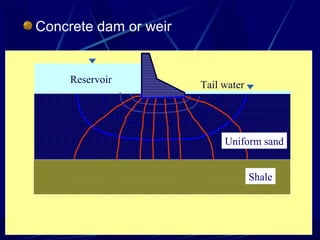
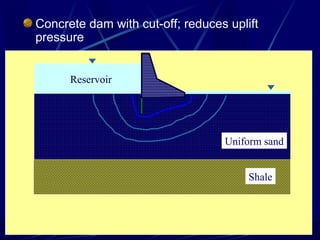
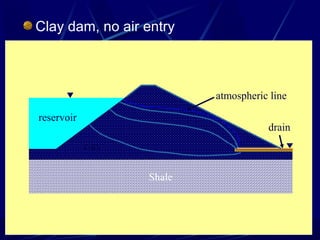
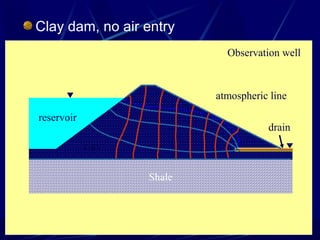
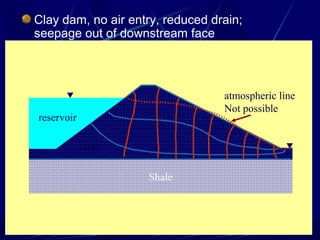
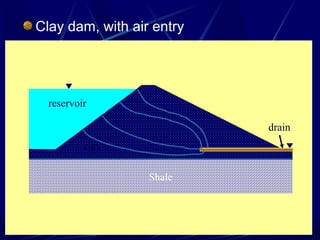
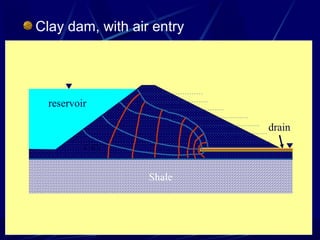
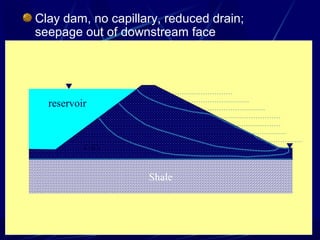
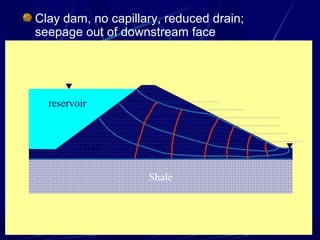
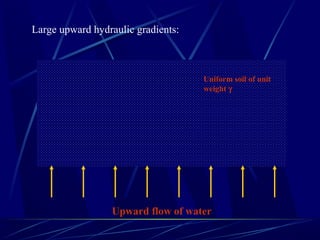
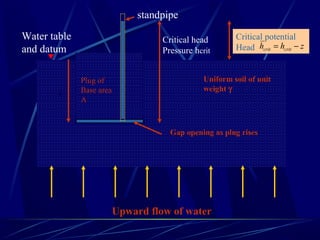
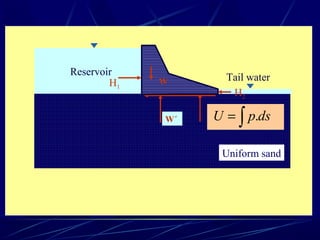
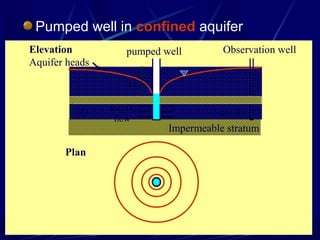
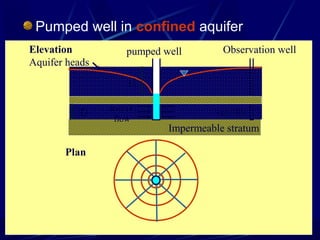
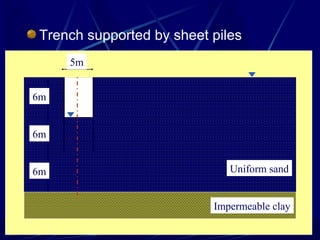
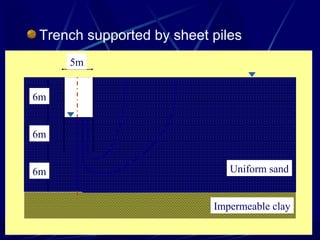
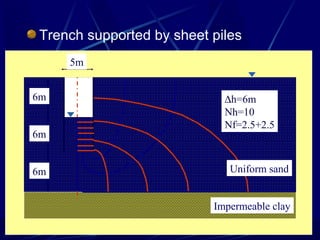
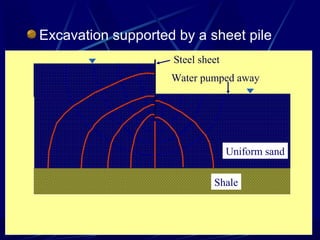
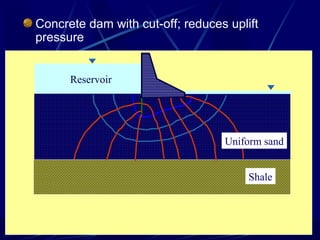
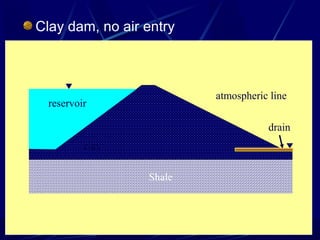
1. The document contains illustrations of various flow nets showing groundwater flow through soils and structures like dams and excavations. 2. Flow nets illustrate groundwater flow under steady state and unsteady state conditions, taking into account factors like soil permeability, capillarity, consolidation, and liquefaction potential. 3. Examples of flow nets show flow through dams made of clay, sand and concrete, as well as flow around excavations supported by sheet piles.

1. Illustrations of
flow nets
3D6 Environmental Engineering II
Dr Gopal Madabhushi

2. Trench supported by sheet piles
Impermeable clay
Uniform sand
5m
6m
6m
6m

3. Trench supported by sheet piles
Impermeable clay
Uniform sand
5m
6m
6m
6m

4. Trench supported by sheet piles
Impermeable clay
5m
6m
6m
6m
∆h=6m
Nh=10
Nf=2.5+2.5
Uniform sand

5. Excavation supported by a sheet pile
Shale
Uniform sand
Water pumped away
Steel sheet

6. Excavation supported by a sheet pile
Shale
Uniform sand
Water pumped away
Steel sheet

7. Reduced sheet penetration; possible
liquefaction σ′v = 0
Shale
Uniform sand
Steel sheet

8. Reduced sheet penetration; possible
liquefaction σ′v = 0
Uniform sand
Reservoir Tail water
Shale

9. Concrete dam or weir
Reservoir Tail water
Shale
Uniform sand

10. Concrete dam with cut-off; reduces uplift
pressure
Reservoir
Shale
Uniform sand

11. Concrete dam with cut-off; reduces uplift
pressure
Reservoir
Shale
Uniform sand

12. Pumped well in confined aquifer
Observation wellpumped wellElevation
Aquifer heads
H
D aquiferRadial
flow
Impermeable stratum
Plan

13. Pumped well in confined aquifer
Observation wellpumped wellElevation
Aquifer heads
H
D aquiferRadial
flow
Impermeable stratum
Plan

14. Clay dam, no air entry
Shale
clay
reservoir
atmospheric line
drain

15. Clay dam, no air entry
Shale
clay
atmospheric line
drain
reservoir

16. Clay dam, no air entry
Observation well
Shale
clay
atmospheric line
drain
reservoir

17. Clay dam, no air entry, reduced drain;
seepage out of downstream face
Shale
clay
atmospheric line
Not possible
reservoir

18. Clay dam, with air entry
Shale
clay
reservoir
drain

19. Clay dam, with air entry
Shale
clay
reservoir
drain

20. Clay dam, no capillary, reduced drain;
seepage out of downstream face
Shale
clay
reservoir

21. Clay dam, no capillary, reduced drain;
seepage out of downstream face
Shale
clay
reservoir

22. Flow of water in earth dams
The drain in a rolled clay dam will be
made of gravel, which has an effectively
infinite hydraulic conductivity compared
to that of the clay, so far a finite quantity
of flow in the drain and a finite area of
drain the hydraulic gradient is effectively
zero, i.e. the drain is an equipotential

23. The phreatic surface connects points at which
the pressure head is zero. Above the phreatic
surface the soil is in suction, so we can see
how much capillarity is needed for the
material to be saturated. If there is insufficient
capillarity, we might discard the solution and
try again. Alternatively: assume there is zero
capillarity, the top water boundary is now
atmospheric so along it and the flow
net has to be adjusted within an unknown top
boundary as the phreatic surface is a flow line
if there is no capillarity.
Flow of water in earth dams
yh =

24. If then in the flow net,
so once we have the phreatic surface
we can put on the starting points of the
equipotentials on the phreatic surface
directly
Flow of water in earth dams
yh = consyh == δδ

25. Unsteady flow effects
Consolidation of matrix
Change in pressure head within the soil due to
changes in the boundary water levels may
cause soil to deform, especially in
compressible clays. The soil may undergo
consolidation, a process in which the voids
ratio changes over time at a rate determined
by the pressure variation and the hydraulic
conductivity, which may in turn depend on the
voids ratio.

26. Liquefaction (tensile failure)
The total stress σ normal to a plane in the soil can be separated
into two components, the pore pressure p and the effective
inter-granular stress σ’:
By convention in soils compressive stresses are +ve.
Tensile failure occurs when the effective stress is less than the
fracture strength σ’fracture, and by definition for soil σ’fracture=0.
When the effective stress falls to zero the soil particles are no
longer in contact with each other and the soil acts like a heavy
liquid. This phenomenon is called liquefaction, and is
responsible to quick sands.
Breakdown of rigid matrix
p+′= σσ

27. Uniform soil of unit
weight γ
Upward flow of water
Large upward hydraulic gradients:

28. Uniform soil of unit
weight γ
Upward flow of water
Plug of
Base area
A
Water table
and datum
standpipe
Gap opening as plug rises
Critical head
Pressure hcrit
Critical potential
Head zhh critcrit −=
z

29. At the base of the rising plug, if there is no side friction:
wcrit
v
hp
z
γ
γσ
.
.
=
=
So if σv′=0 then σv = p and :
( ) wcritwcrit zhhz γγγ ... +==
w
wcrit
crit
z
h
i
γ
γγ −
== , icrit=0.8~1.0

30. where icrit is the critical hydraulic gradient for the quick sand
Condition. As γ ≅ 18~20 kN/m3
for many soils (especially sands
and silts) and γw ≅ 10 kN/m3
:
0.1
10
1020
=
−
==
z
h
i crit
crit

31. Frictional (shear failure)
Sliding failure of a gravity concrete dam due to
insufficient friction along the base:

32. Uniform sand
Reservoir
Tail waterWH1
H2
W´ ∫= dspU .

33. Limiting condition on shear force T is:
maxmax tan. φ′′= WT
where tanφ’max is the co-efficient of friction, so
considering the base of the dam we are looking for:
21max HHF −>
where W‘ = W-U is the effective weight of the dam, U is the
total uplift due to the pore pressure distribution p along the base
of the dam, and F = H1- H2 is the shear force along the
Dam base