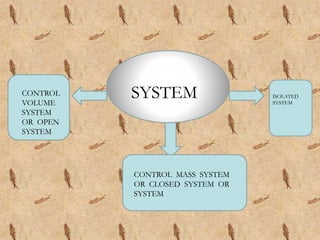
This document discusses Reynolds transport theorem and its application to conservation of mass in fluid flow using a control volume approach. It defines key terms like system, control mass system, control volume system, and isolated system. It also presents the continuity equation in differential and integral form for a control volume. The Reynolds transport theorem relates how the rate of change of an extensive property within a system equals the rate of change within a control volume plus the net rate of efflux from the control volume. As an example, it shows how the conservation of mass statement for a system and control volume are related using the Reynolds transport theorem.

1. BY- MOHIT MAYOOR KASHYAP
CUJ/I/2013/IWEM/007

2. INTRODUCTION
• Reynolds transport theorem is a theorem which is used to
relate statement of any physical law to a system to the
statement of that physical law to a control volume.

3. • Mathematically,
• Time rate of change of any extensive
property for a system = rate of change of
property within a control volume + net rate of
efflux of the property from the control volume
• N= property η = property/mass
• {DN/Dt}system = {δ/δt ∫ ∫ ∫ η ρdv }control volume +
{∫ ∫ η ρv.dA}control surface

4. IMPORTANT POINTS
• A particle is a differential concept of system.
• Any thing is defined with respect to system .
• Basic laws are first initiated with respect to system.
• But later on , it was much simplified by defining the basic
laws with respect to control volume.

6. • SYSTEM- some amount of mass and boundary.
• Mass and boundary are the important characteristics of
the system.
surroundingMass system
boundary

7. SYSTEM
CONTROL MASS SYSTEM
OR CLOSED SYSTEM OR
SYSTEM
CONTROL
VOLUME
SYSTEM
OR OPEN
SYSTEM
ISOLATED
SYSTEM

8. CONTROL MASS SYSTEM
• Mass transfer is not allowed.
• So identity remains constant
• Boundary may contract or expand as energy transfer is
allowed, so the boundary is flexible.
M closed
No mass
transfer

9. CONTROL VOLUME SYSTEM
• Also known as open system.
• In this kind of system mass and energy transfer both take
place , so identity is lost.
• Boundary is rigid.

10. ISOLATED SYSTEM
• No mass transfer and no energy transfer.
• It is isolated from the surrounding.

11. • Let us take an example of conservation of mass in fluid flow.
• e.g. for system :-{ dm/dt = 0 } rate of change of
mass within a system is zero i.e. mass remains
constant inside the system.
• For control volume- continuity equation states
that the net rate of increase in mass in the
control volume + net rate of mass efflux from
the control volume = 0

12. CONTINUITY EQUATION FOR
CONTROL VOLUME
• δρ/δt +δ(ρu)/δx + δ(ρv)/δy + δ(ρw)/δz = 0
• DIFFERENTIAL FORM
• δρ/δt + ∇. (ρV)
Where ∇ = i δ/ δx + j δ/ δy + k δ/ δz
V= iu + jv + kw

13. • CONTINUITY EQUATION IN
INTEGRAL FORM
• Net rate of mass efflux from c.v. = ∫ ∫ A ρV.ndA
• Net rate of increase of mass in cv = ∫ ∫ ∫v ρdv
CONTROL
VOLUME
dA

14. RTT APPLICATION
• CONSERVATION OF MASS
• Let N= mass= m Dm/Dt=0 {wrt system}
• η=1 {N/mass}
• Dm/Dt= δ/ δt∫ ∫ ∫cv ρdv + ∫ ∫ cs Ρv. dA
0

15. • CUJ/I/2103/IWEM/007
• THANKS