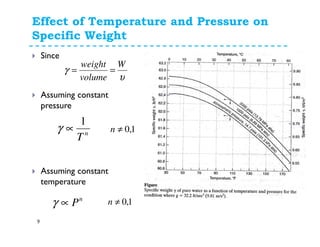
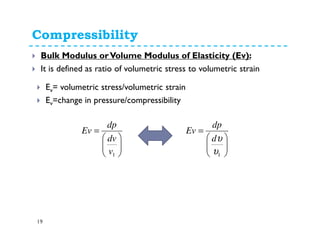
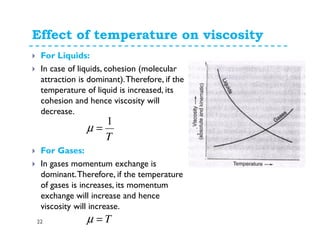
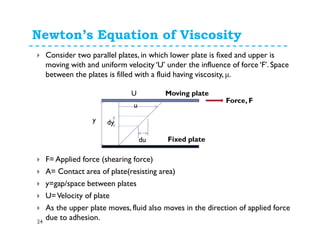
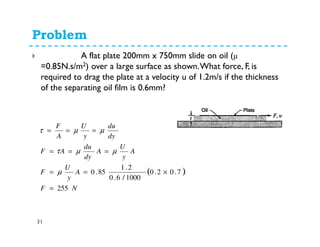
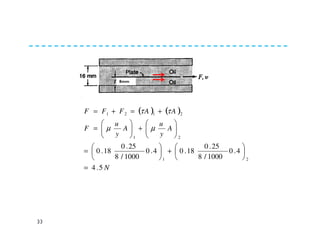
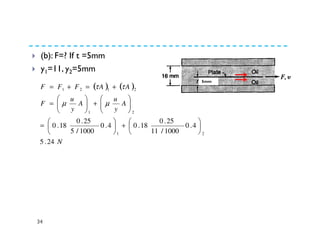
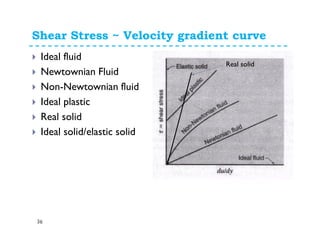
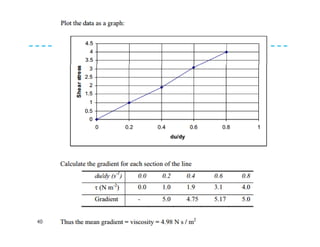
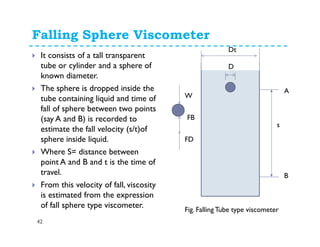
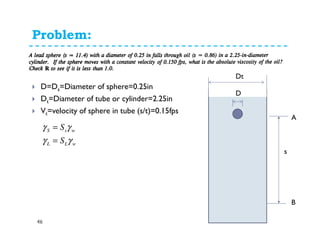
Fluid properties such as density, specific volume, specific weight, specific gravity, compressibility, viscosity, and surface tension are discussed. Density is defined as the mass of a substance per unit volume. Specific volume is defined as the volume of substance per unit mass. Specific weight is the weight of substance per unit volume. Specific gravity is the ratio of density of a substance to the density of water. Compressibility refers to the change in volume of a fluid with changes in pressure. Viscosity is a measure of a fluid's resistance to shear forces and depends on factors like cohesion and molecular momentum. The falling sphere viscometer is used to measure viscosity and involves dropping a sphere in a fluid and measuring its velocity over

1. Fluid Properties: Density, specific volume, specific
weight, specific gravity, compressibility, viscosity,
measurement of viscosity, Newton's equation of
viscosity, Surface tension, capillarity and pressure
Dr. Mohsin Siddique
Assistant Professor
1
Fluid Mechanics

2. Physical Properties of Fluids
2
Density
SpecificVolume
SpecificWeight
Specific Gravity
Compressibility
Viscosity
SurfaceTension
Pressure
Buoyancy

3. Density
3
It is also termed as specific mass or mass density.
It is the mass of substance per unit volume .i.e., mass of fluid per
unit volume.
It is designated with symbol of ρ (rho)
ρ =mass/volume
=M/L3
Fundamental Units=kg/m3, slug/m3, g/cm3
4
2
3
2
L
FT
L
M
L
FT
a
F
MMaF
==
==⇒=
ρ
Note: Density of water at 4oc=1000kg/m3, 1.938slug/ft3, 1g/cm3

4. Specific Volume
4
It is defined as volume of substance per unit mass.
It is designated with υ.
MLmassvolume // 3
==υ
MaF =
2
4
FT
L
=υ
Fundamental Units=m3/kg, m3/slug, cm3/g

5. Relationship Between Mass and Specific Volume
5
3
3
//
//
LMvolumemass
MLmassvolume
==
==
ρ
υ
υρ
ρυ
/1
/1
=
=

6. Specific Weight
6
It is the weight of substance per unit volume or say it is
the weight of fluid per unit volume.
It is designated by γ (gamma).
3
L
W
volume
weight
==γ 3
L
Mg
=γ MgW =Q
2223
TL
M
TL
ML
==γ 2
T
L
g =Q
Note: Specific weight of water at 4oc=9810N/m3, 62.4lb/ft3, 981dyne/cm3

7. Relation Between and
7
volume
weight
volume
Mass
== γρ &
γ ρ
gργ =
MgW =Q

8. Effect of Temperature and Pressure on
Specific Weight
8
As the equation of state for a
perfect gas is given by
Where
P=absolute pressure
υ=specific volume
T=absolute temperature
R=gas constant
For perfect gases
mR=8312N-m/(kg-k)
Where
m=molecular weight of gas
RTP =υ ρ
υ
1
=QRT
P
=
ρ
( )
RT
g
P
=
/γ g
γ
ρ =Q
RT
gP
=γ
T
P
constt=γ
R
g
constt =
T
P
1
& ∝∝ γγ
RTP =υ

9. Effect of Temperature and Pressure on
Specific Weight
9
Since
Assuming constant
pressure
Assuming constant
temperature
υ
γ
W
volume
weight
==
n
T
1
∝γ
n
P∝γ
1,0≠n
1,0≠n

10. Specific Gravity (Relative Density)
10
It is the ratio of density of a substance and density of water at 4oC.
It is the ratio of specific weight of substance and specific weight of
water at 4oC.
It is the ratio of weight of substance and weight of an equal volume
of water at 4oC.
water
fluid
water
fluid
water
fluid
W
W
S ===
γ
γ
ρ
ρ
Remember:
T
P
1
& ∝∝ γγ
CTatW
CTatW
CTat
CTat
CTat
CTat
S o
water
o
fluid
o
water
o
fluid
o
water
o
fluid
===
γ
γ
ρ
ρ
Note: Specific gravity of liquid is measure w.r.t. water while for
cases of gases it is measured w.r.t. standard gas (i.e., air)

11. PROBLEMS
11

12. PROBLEMS
12

13. PROBLEMS
13

14. 14

15. Compressibility
Compressible fluids
Incompressible fluids
In fluid mechanics we deal with both compressible and
incompressible fluids of either variable or constant density.
Although there is no such thing in reality as incompressible fluid, we
use this terms where the change in density with pressure is so small
as to be negligible.This is usually the case with liquids.
Ordinarily, we consider the liquids as incompressible.
We may consider the gases to be incompressible when the pressure
variation is small compared with absolute pressure.

16. Compressibility
16
Compressible fluids
Fluids which can be compressed.
Fluid in which there is a change in volume with change in pressure
P1
P2
v1
v2
12 PP >
12 vv <
As a result of change in volume,
density and specific weight of
fluid also changes. Hence, for
compressible fluids,
21
21
21
γγ
ρρ
≠
≠
≠ vv

17. Compressibility
17
Incompressible fluids
Fluids which can not be compressed.
Fluid in which there is no change in volume with change in pressure
P1 P2
v1
v2
12 PP >
12 vv =
As a result of change in volume,
density and specific weight of
fluid also changes. Hence, for
compressible fluids,
21
21
21
γγ
ρρ
=
=
= vv
v2

18. Compressibility (Volumetric Strain)
18
Volumetric Strain is the ratio of change in volume and original volume.
P1
P2
v1
v2
12 PP >
12 vv <
11
21
1
21
21
1
21
/
//
v
dv
v
vv
Mv
MvMv
v
=
−
=
−
=
>
−
= υυ
υυ
Q
Volumetric strain=change in specific volume/original specific volume.
1
21
1
21
υ
υ
υυ
υ
υυ
d
=
>
−
= Q

19. Compressibility
19
Bulk Modulus orVolume Modulus of Elasticity (Ev):
It is defined as ratio of volumetric stress to volumetric strain
Ev= volumetric stress/volumetric strain
Ev=change in pressure/compressibility






=
1v
dv
dp
Ev






=
1υ
υd
dp
Ev

20. Viscosity
20
The viscosity of a fluid is a measure of its resistance to shear or
angular deformation.
It is the property of a fluid by mixture of which it offers
resistance to deformation under the influence of shear forces.
It depends upon the cohesion and molecular momentum
exchange between fluid layers.
It can also be defined as internal resist offered by fluid to flow.
It is denoted by µ.
It is also termed as coefficient of viscosity or absolute viscosity or
dynamic viscosity or molecular viscosity.

21. Factor affecting viscosity
21
1. Cohesion
2. Molecular momentum
1. Cohesion: It is the attraction between molecules of fluid. More
the molecular attraction (cohesion) more is the viscosity (resistance
to flow) of fluid.
It is dominant in liquids.
2. Molecular momentum: Molecules in any fluid change their
position with time and is known as molecular activity. More the
molecular activity more will be viscosity of the fluid.
It is dominant in gases
A
B

22. Effect of temperature on viscosity
22
For Liquids:
In case of liquids, cohesion (molecular
attraction is dominant).Therefore, if the
temperature of liquid is increased, its
cohesion and hence viscosity will
decrease.
For Gases:
In gases momentum exchange is
dominant.Therefore, if the temperature
of gases is increases, its momentum
exchange will increase and hence
viscosity will increase.
T
1
=µ
T=µ

23. Kinematic Viscosity
23
It is ratio of absolute viscosity and density of fluid.
It is denoted by (nu)ν
ρ
µ
ν =

24. Newton’s Equation of Viscosity
24
Consider two parallel plates, in which lower plate is fixed and upper is
moving with and uniform velocity ‘U’ under the influence of force ‘F’. Space
between the plates is filled with a fluid having viscosity, µ.
F= Applied force (shearing force)
A= Contact area of plate(resisting area)
y=gap/space between plates
U=Velocity of plate
As the upper plate moves, fluid also moves in the direction of applied force
due to adhesion.
y
u
dy
du
U Moving plate
Fixed plate
Force, F

25. Newton’s Equation of Viscosity
25
Factor affecting Force, F
Hence,
Where, µ is coefficient of viscosity
Assuming linear velocity profile (as shown in figure)
y
FiiiUFiiAFi
1
)(;)(;)( ∝∝∝
y
AU
F ∝
y
AU
F µ=
dy
du
y
U
A
F
µµτ ===

26. Newton’s Equation of Viscosity
26
At boundaries the particles of fluid adhere to wall and so their velocities are
zero relative to wall.This so called non-slip condition occurs in viscous fluids

27. Newton’s Equation of Viscosity
27
The above equation is called as Newton’s equation of viscosity.
The equation shows that the shearing stress is directly proportional
to the velocity gradient and its is known as Netwon’s law of
velocity.
In the above equation
du/dy= velocity gradient or rate of change of deformation
µ = absolute viscosity
τ=shear stress
dy
du
µτ =

28. Dimensional Analysis of Viscosity
28
Viscosity
This expression is used to write
fundamental unit of viscosity
KinematicViscosity
2
2
)/(
L
FT
TLL
FL
U
y
A
F
=
==
µ
µ
T
L
L
M
LT
M
2
3
===
ρ
µ
ν
LT
M
MLTF
L
TMLT
=
== −
−
µ
µ 2
2
2
Q

29. Unit of Viscosity
29
Viscosity
Widely used unit is Poise =0.1N.s/m2
KinematicViscosity
Widely used unit is Stoke=10-4m2/s
LTM /=µ
TL /2
=ν
SI BG CGS
N-s/m2 Lb-s/ft2 Dyne-s/cm2
(Poise, P)
Kg/(m-s) Slug/(ft-s) g/(cm-s)
SI BG CGS
m2/s ft2/s cm2/s
(stoke)

30. Problem
30

31. Problem
31
Q. 2.11.4: A flat plate 200mm x 750mm slide on oil (µ
=0.85N.s/m2) over a large surface as shown.What force, F, is
required to drag the plate at a velocity u of 1.2m/s if the thickness
of the separating oil film is 0.6mm?
( )
NF
A
y
U
F
A
y
U
A
dy
du
AF
dy
du
y
U
A
F
255
7.02.0
1000/6.0
2.1
85.0
=
×==
===
===
µ
µµτ
µµτ

32. Problem
32
Q.2.11.8: A space 16mm wide between two large plane surfaces is
filled with SAE 30 Western lubricating oil at 35oC(Fig11.8).What
force is required to drag a very thin plate of 0.4m2 area between the
surfaces at a speed u=0.25m/s (a) if this plate is equally spaced
between the two surfaces? (b) if t=5mm?
Solution:
Y=16mm A=0.4m2 u=0.25m/s
T=35oC µ =0.18N.s/m2 (from figure A.1)
F=? If y=8mm
(a)
8mm
dy
du
y
U
A
F
µµτ ===
( ) ( )2121 AAFFF ττ +=+=

33. 33
8mm
( ) ( )
N
A
y
u
A
y
u
F
AAFFF
5.4
4.0
1000/8
25.0
18.04.0
1000/8
25.0
18.0
21
21
2121
=






+





=






+





=
+=+=
µµ
ττ

34. 34
(b): F=? If t =5mm
y1=11, y2=5mm
( ) ( )
N
A
y
u
A
y
u
F
AAFFF
24.5
4.0
1000/11
25.0
18.04.0
1000/5
25.0
18.0
21
21
2121






+





=






+





=
+=+=
µµ
ττ
5mm

35. 35

36. Shear Stress ~ Velocity gradient curve
36
Ideal fluid
Newtownian Fluid
Non-Newtownian fluid
Ideal plastic
Real solid
Ideal solid/elastic solid
Real solid

37. Shear Stress ~ Velocity gradient curve
37
Ideal Fluid: The fluid which does not offer resistance to flow
Newtownian Fluid: Fluid which obey Newtown’s law of viscosity
slope of curve ( )is constant
Non-Newtonian fluid: Fluid which does not obey Newtown’s Law
of viscosity
slope of curve ( )changing continuously
dy
du
∝τ
00 =⇒= τµ
dy
du
∝τ
dydu /~τ
dydu /~τ

38. Shear Stress ~ Velocity gradient curve
38
Ideal Solid: solid which can never be deformed under the action of
force
Real solid: solid which can be deformed under action of forces
Ideal Plastic: These are substances which offer resistance to shear
forces without deformation upon a certain extent but if the load is
further increased then they deform
Real Plastic: These are substances in which there is deformation
with the application of force and it increases with increase in applied
load.
0=
dy
du

39. Problem
39

40. 40

41. Measurement of Viscosity
41
The following devices are used for the measurement of viscosity
1.Tube type viscometer
2. Rotational type viscometer
3. Falling sphere type viscometer

42. Falling Sphere Viscometer
42
It consists of a tall transparent
tube or cylinder and a sphere of
known diameter.
The sphere is dropped inside the
tube containing liquid and time of
fall of sphere between two points
(say A and B) is recorded to
estimate the fall velocity (s/t)of
sphere inside liquid.
Where S= distance between
point A and B and t is the time of
travel.
From this velocity of fall, viscosity
is estimated from the expression
of fall sphere type viscometer.
s
A
B
Fig. Falling Tube type viscometer
W
FB
FD
Dt
D

43. Falling Sphere Viscometer
43
D=Ds=Diameter of sphere
Dt=Diameter of tube or cylinder
Vt=velocity of sphere in tube (s/t)
s=Distance between point s A and B
t=time taken by sphere to cover
distance, s
W=weight of sphere=γ(Vol)
= γs(πD3/6)
FB=Force of Buoyancy
= γL(πD3/6)
FD=Drag force
= (3πµVD)
Note: V is not equal to Vt
s
A
B
Fig. Falling Tube type viscometer
W
FB
FD
Dt
D
Stoke’s Law

44. Falling Sphere Viscometer
44
Bouyancy: It is the resultant upward thrust exerted by the fluid on a
sphere. It is the tendency of fluid to lift the body and it is equal to weight
of volume of fluid displaced by the body (Archimedes Principal).
Drag Force: It is a resisting force generated by the liquid on the moving
object which is acting in the opposite direction of movement .
Vt=velocity of sphere in tube with wall effect
V=velocity of sphere in tube without wall effect
V>Vt
...
4
9
4
9
1
2
+





+





+≈
ttt D
D
D
D
V
V
3
1
≤
tD
D
if






=+





=−+=∑
6
3
6
;0;0
33
D
VD
D
WFFF
SL
DBy
π
γπµ
π
γ

45. Falling Sphere Viscometer
45
The above equation is governing equation for falling sphere type
viscometer.
For a particular temperature, D, γs and γL are constant. So we can
write ;
Thus, velocity of fall is inversely proportional to viscosity and
is indicative of viscosity in falling sphere type viscometer.
Note: This method can only be used for transparent liquids
( )LS
LSLS
V
D
DD
V
DD
VD
γγµ
γγµ
π
γ
π
γπµ
−=






−





=⇒





−





=
18
66
3
66
3
2
2233
V
1
αµ

46. Problem: 11.1.10
46
D=Ds=Diameter of sphere=0.25in
Dt=Diameter of tube or cylinder=2.25in
Vt=velocity of sphere in tube (s/t)=0.15fps
wLL
wsS
S
S
γγ
γγ
=
=
s
A
B
Dt
D

47. Problem: 11.1.10
47
( ) 2
2
/.0806.0
18
ftslb
V
D
LS =−= γγµ
3
1
≤
tD
D
if
1
VD
Reno.Reynolds <==
µ
ρ
( ) fpsV
D
D
D
D
V
V
ttt
197.015.0313.1
313.1...
4
9
4
9
1
2
==
=+





+





+≈

48. Surface Tension
48
The tension force created at the imaginary
thin surface due to unbalanced-molecular
attraction is termed as surface tension.
v2 A
B
Molecule A in figure above is situated at a certain depth below the
surface. It is acted upon by equal force from all sides whereas
molecule B (situated at the surface ) is acted upon by unbalanced
forces from below.
Thus a tight skin/film/surface is formed at the surface due to inward
molecular pull.

49. Types of molecular attraction
49
Cohesion: It is the attraction force between the molecules of same
material
Adhesion: It is the attraction force between the molecules of
different materials
Surface tension depends upon the relative magnitude of cohesion
and adhesion but primarily it depend upon the cohesion.
With the increase in temperature cohesion reduces and hence
surface tension also reduces.
Concept of surface tension is used in capillarity action

50. Capillarity
50
It is the rise of fall of liquid in a small diameter (< 0.5”) tube due to
surface tension and adhesion between liquid and solid.
For capillary action diameter of tube is less than 0.5inch while for
large diameter tubes this phenomenon become negligible.
The curved surface that develops in tube is called meniscus
v2
h
σ
θ
D
v2
h
σ
θ
D
Water MercuryΘ<90 Θ>90

51. Capillarity
51
D= diameter of tube
γ=specific weight of liquid
h=capillary rise
θ=angle of contact or contact angle
σ=force of surface tension per unit length
v2
h
σ
θ
D
Derivation of expression for capillary rise/fall
Let’s take
Weight of column of liquid acting downward=
Vertical component of force of surface tension=
∑ = 0Fy
( ) 





= hDvol 2
4
π
γγ
( ) θπσ cosD

52. Capillarity
52
Equating both equations
The above equation is used to compute capillary rise/fall.
Note: Fall has –ve sign
( ) 





= hDD 2
4
cos
π
γθπσ
( )
D
hor
hD
hDD
γ
θσ
θ
γ
σ
π
γθπσ
cos4
cos4
4
cos 2
==






=

53. Problem. 2.29
53
Solution:
At 50oF
With θ=0o
True static height=6.78-1.174in=5.61in
( )
( )
inft
D
h
174.10979.0
12/04.041.62
00509.04cos4
==
==
γ
θσ
ftlbftlb /00509.0/41.62 3
== σγ

54. Vapor Pressure of liquids
54
Vapor Pressure: It is the pressure at which liquid transforms into
vapors or it is the pressure exerted by vapors of liquid.
All the liquids have tendency to
release their molecules in the space
above their surface.
If the liquid in container have limited
space above it, then the surface is filled
with the vapors.
These vapors when released from liquid exert pressure known as
vapor pressure.
It is the function of temperature. More the temperature more will
be vapor pressure.

55. Vapor Pressure of liquids
55
Saturated vapor pressure: It is the vapor pressure that
corresponds to the dynamic equilibrium conditions (saturation) i.e.,
when rate of evaporation becomes equal to rate of condensation
Boiling vapor pressure: The pressure at which vapor pressure
becomes equal to atmospheric pressure.

56. Sample MCQs
56
1.Specific gravity of a liquid is equal to
(a). Ratio of mass density of water to mass density of liquid
(b). inverse of mass density
(c). Ratio of specific weight of liquid to specific weight of water
(d). None of all
2.What happens to the viscosity of a liquid when its temperature is raised?
(a).The viscosity of the liquid increases
(b).The viscosity of the liquid stays the same
(c).The viscosity of the liquid decreases
(d).The temperature of a liquid does not rise
3.What happens to the specific weight of a liquid when its temperature is
raised?
(a). It increases
(b). It stays the same
(c). It decreases
(d).The temperature of a liquid does not rise

57. Sample MCQs
57
4. In a falling sphere viscometer, according to force balance we have
(a). Weight=Drag+Buoyancy
(b). Drag=Weight - Buoyancy
(c). Buoyancy=Weight +Drag
(d). None of all
5.The kinematic viscosity is
(a). Multiplication of dynamic viscosity and density
(b). division of dynamic viscosity by density
(c). Multiplication of dynamic viscosity and pressure
(d). None of the above
6.As a result of capillary action
(a) liquid rise in capillary tube
(b) liquid falls down in capillary tube
© Both (a) and (b)
(d) None of all

58. Thank you
Questions….
Feel free to contact:
58