Solo Hermelin, profile picture
Uploaded bySolo Hermelin
PPT, PDF13,852 views

6 computing gunsight, hud and hms

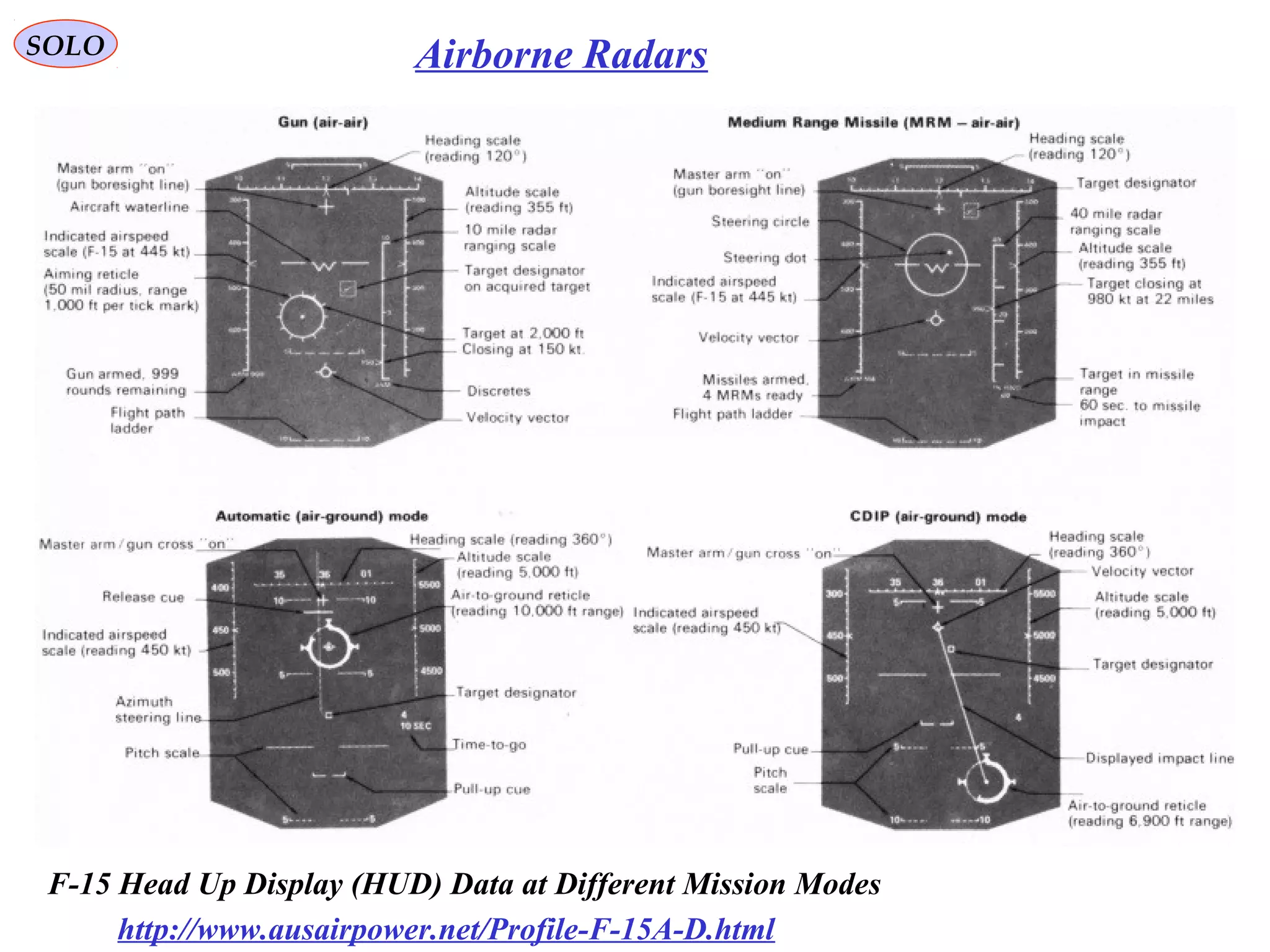
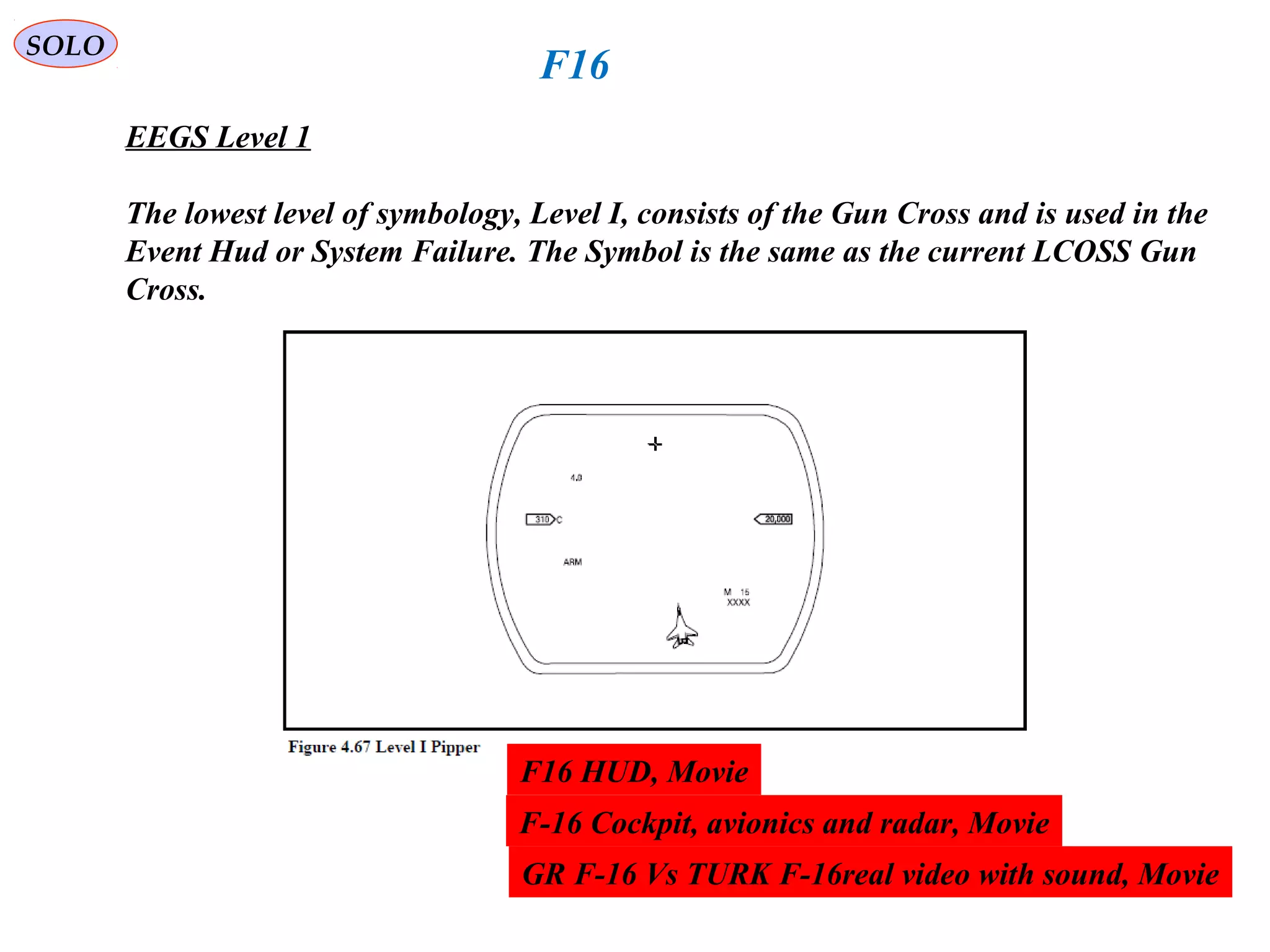
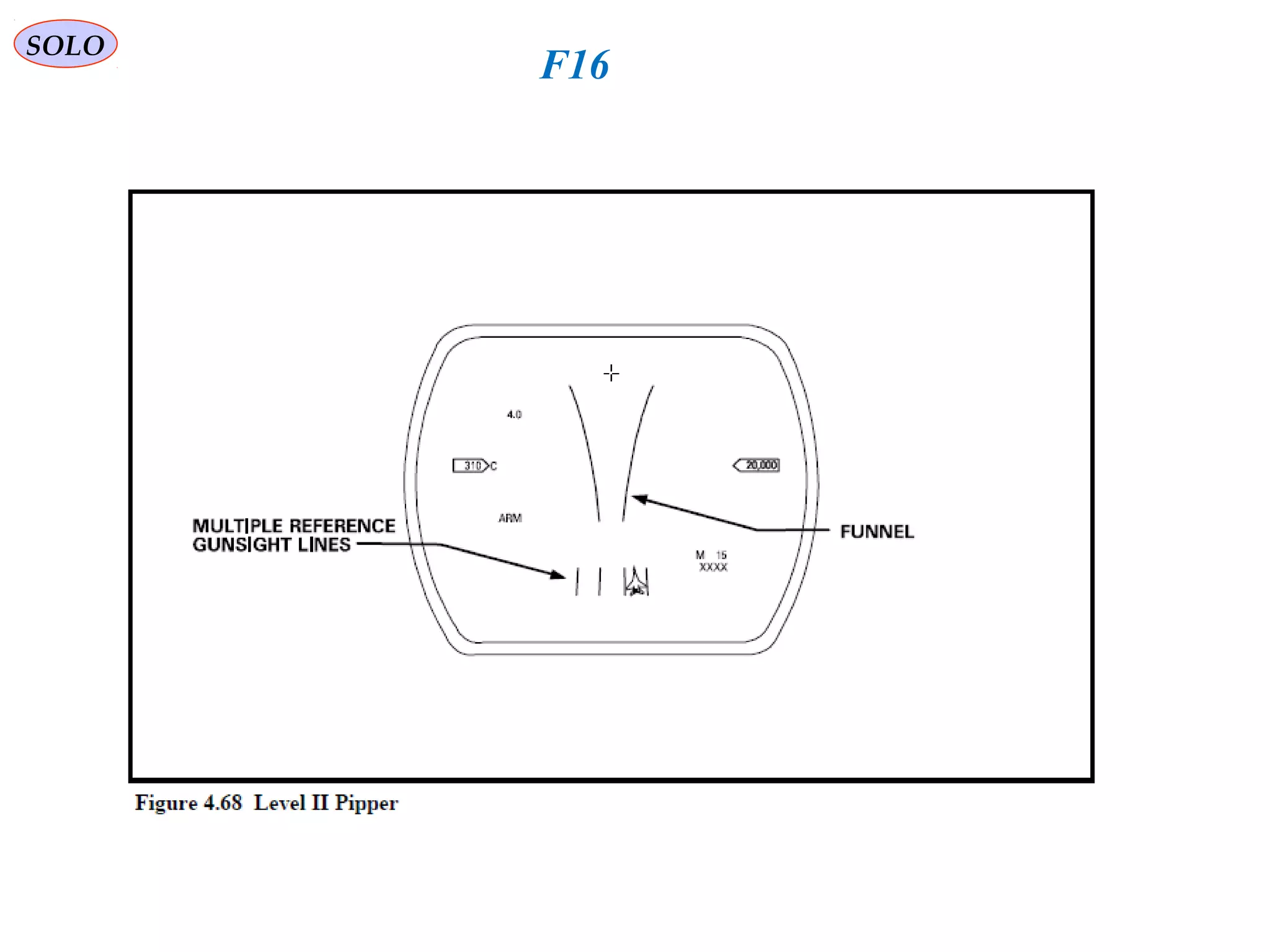
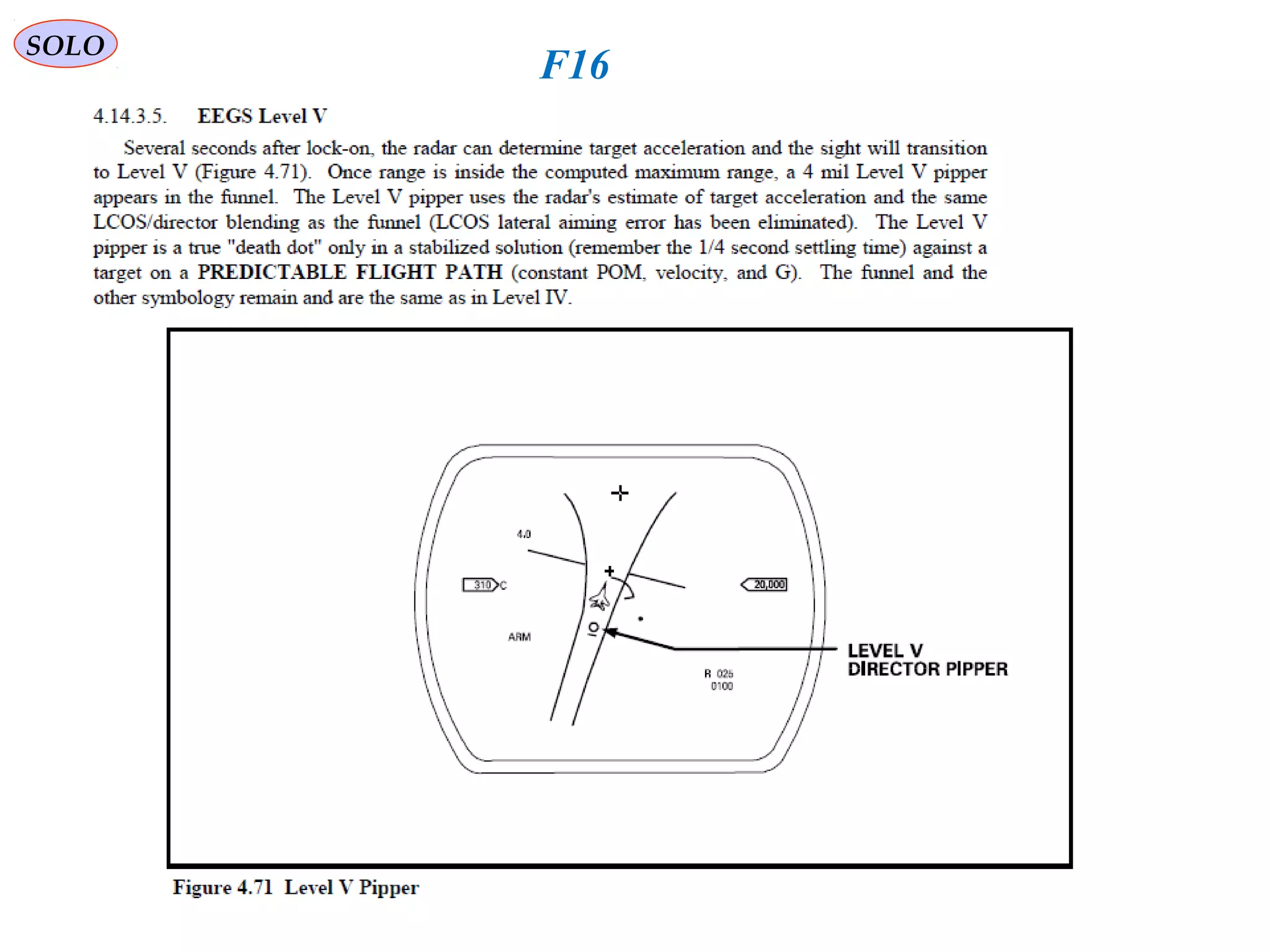
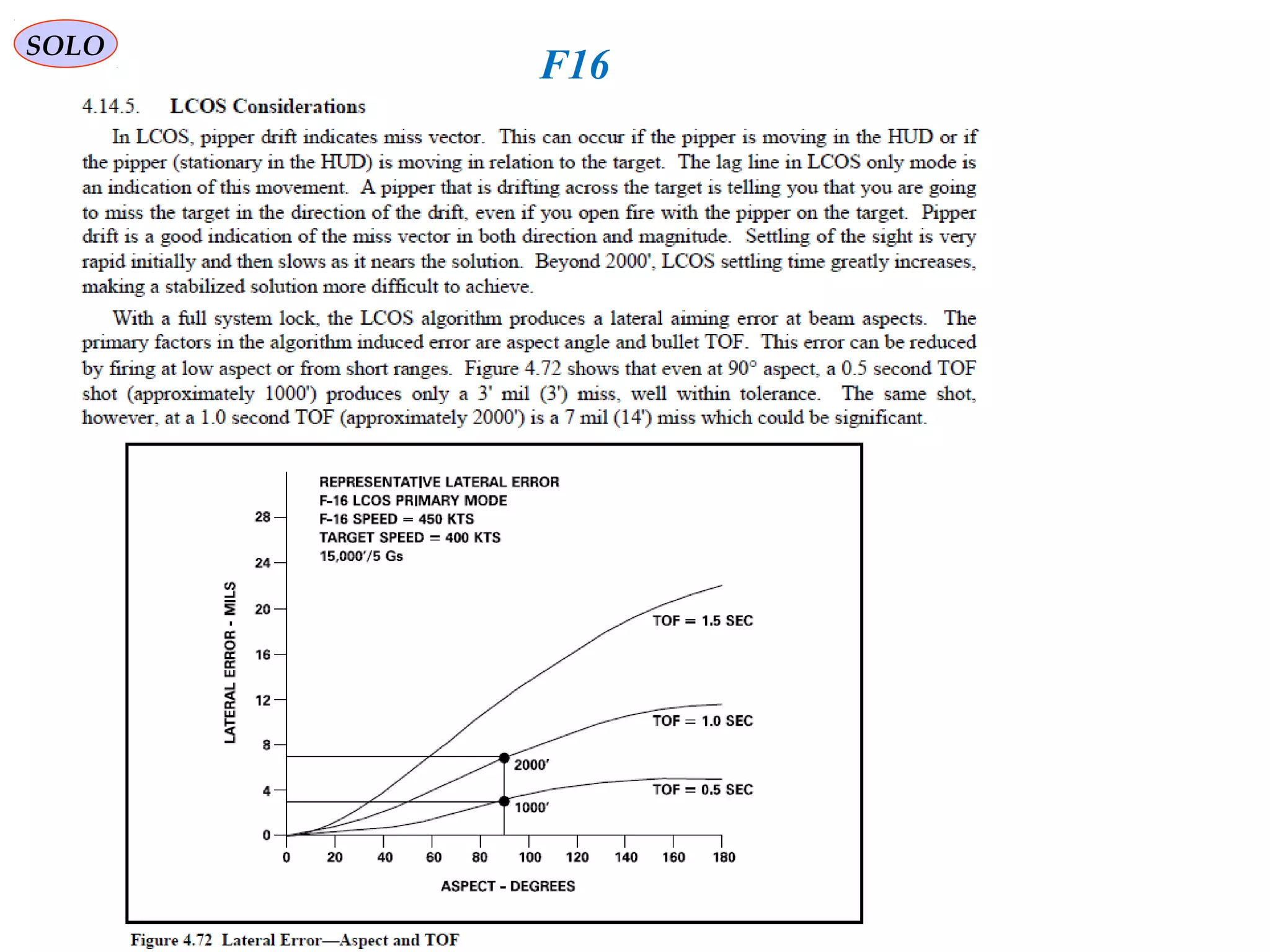
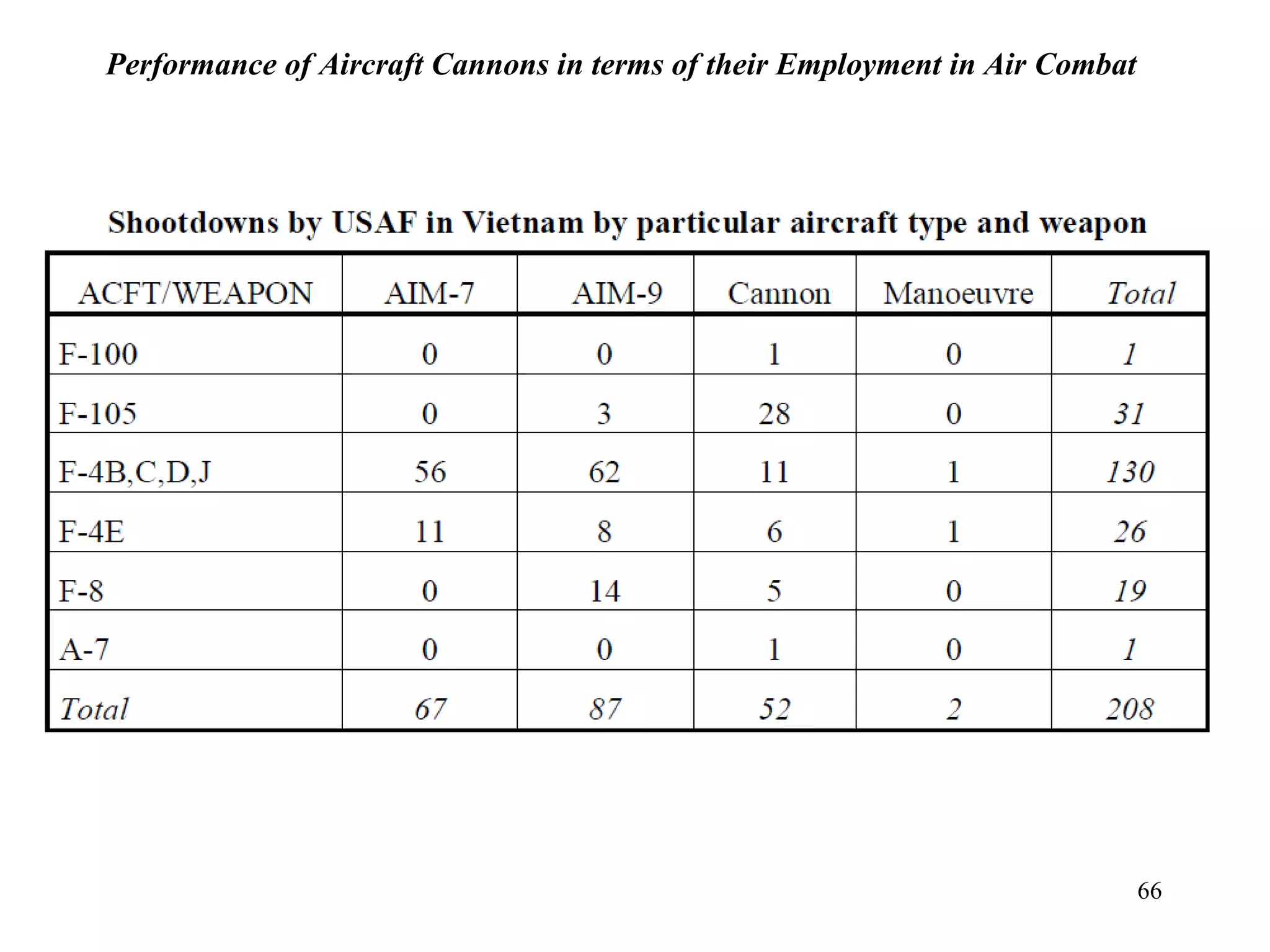
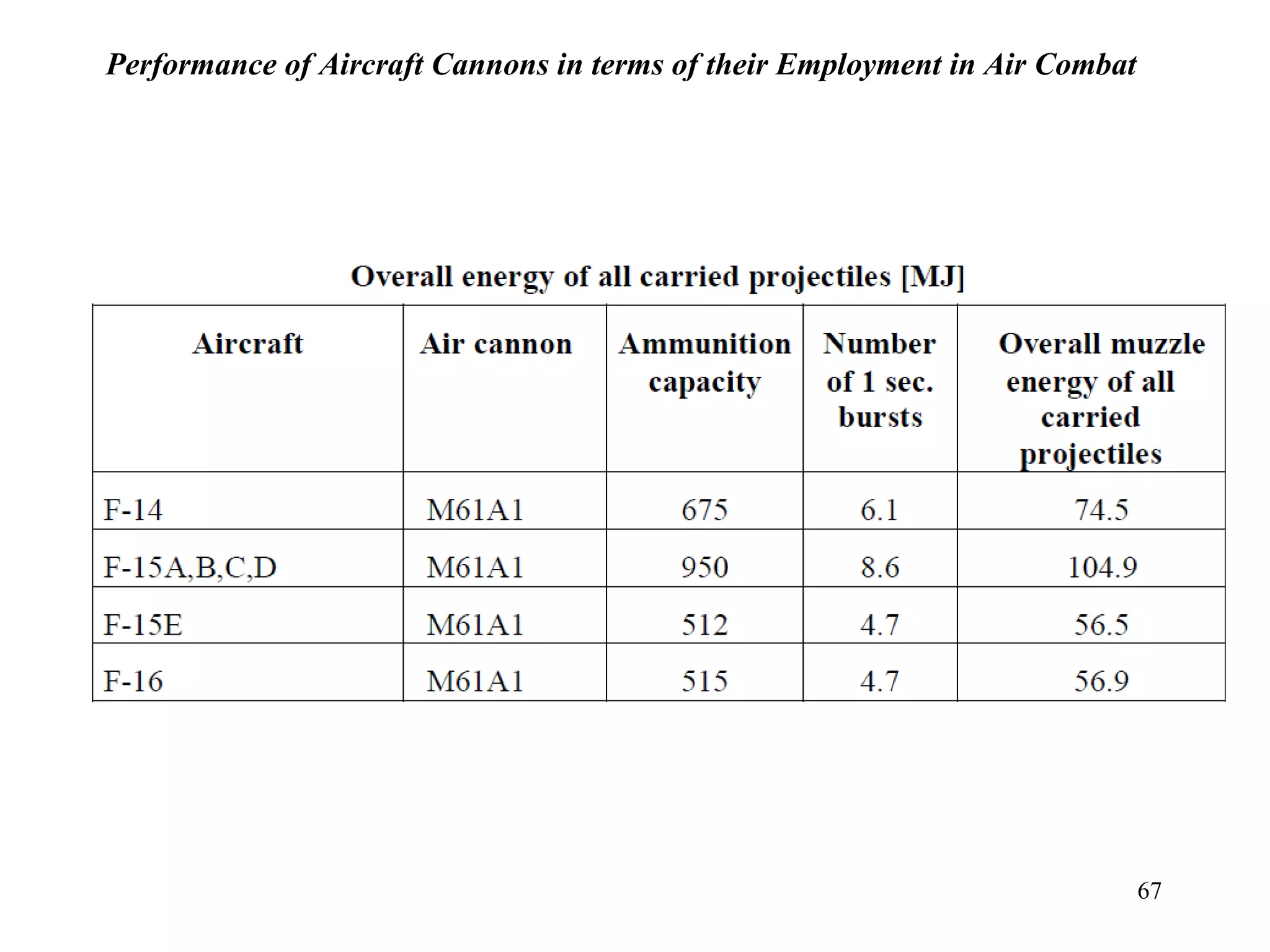
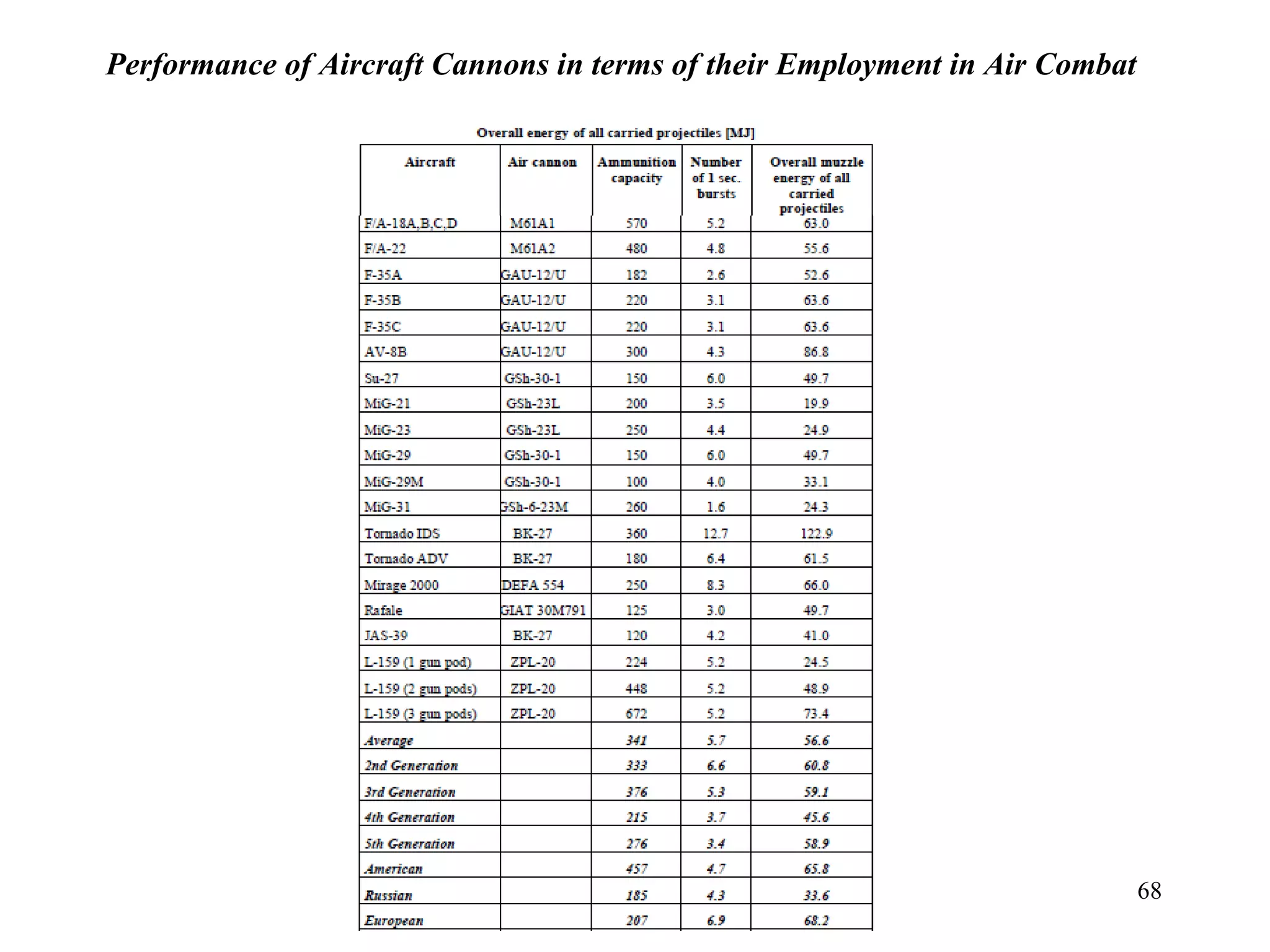
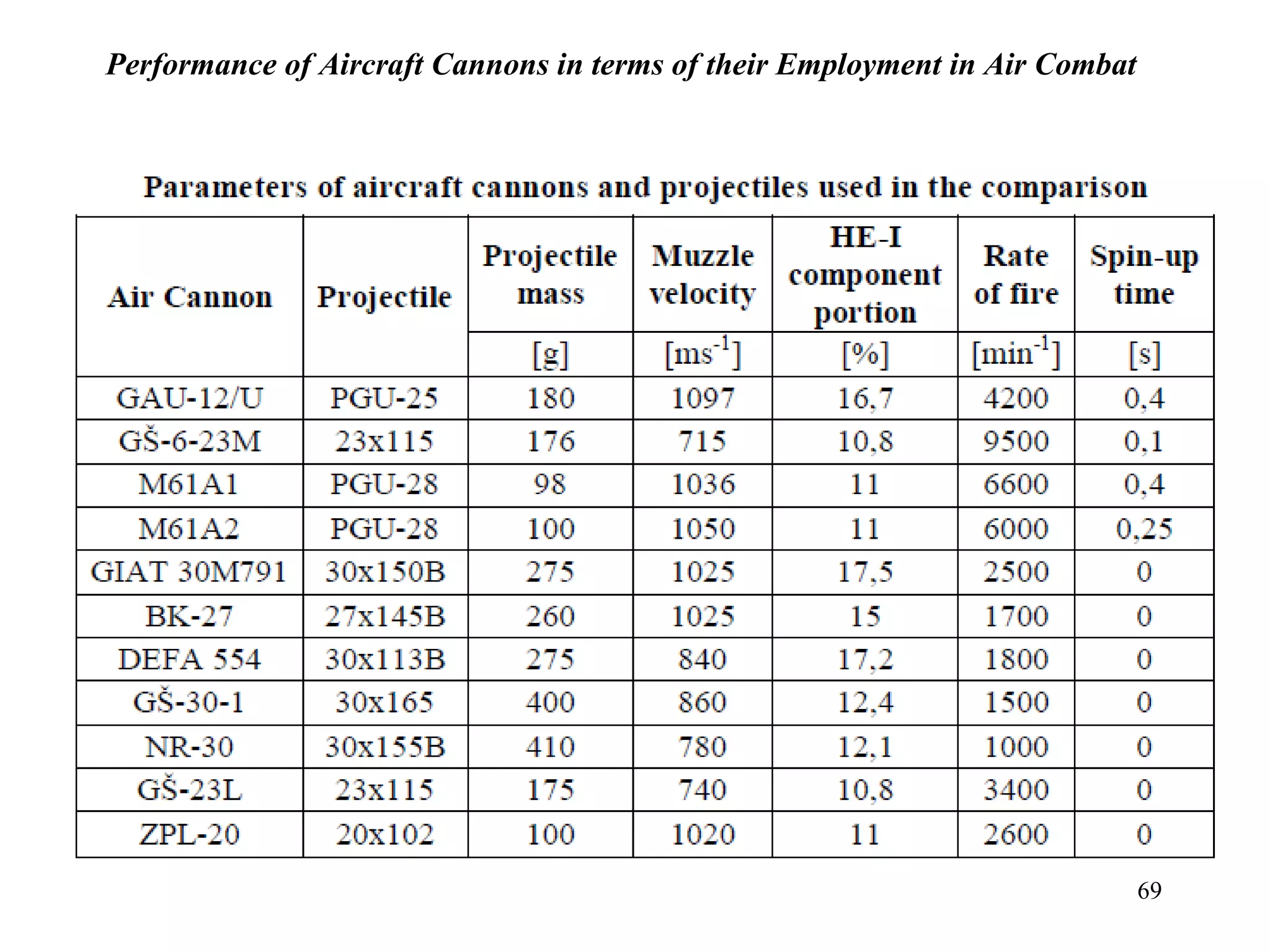
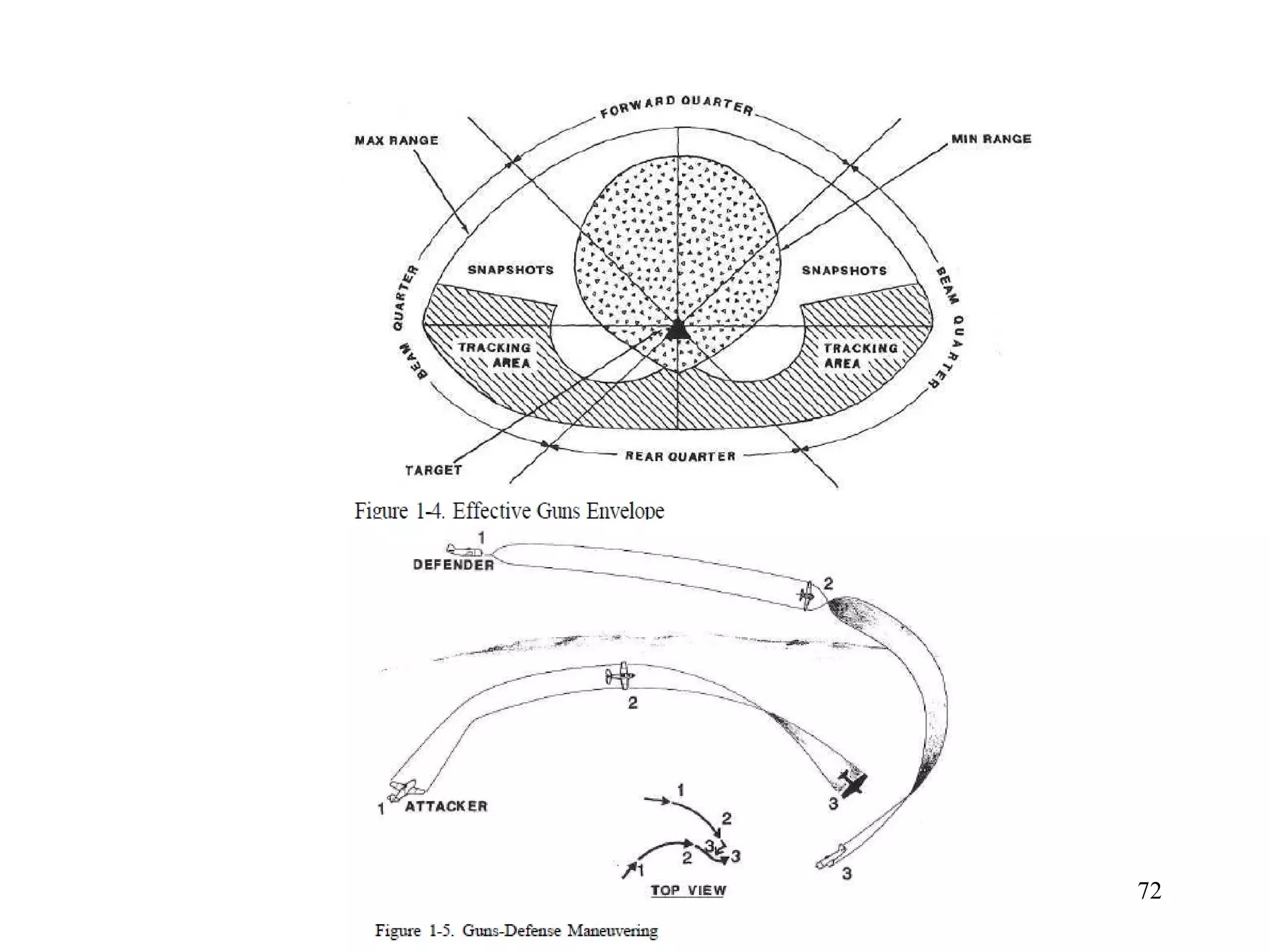
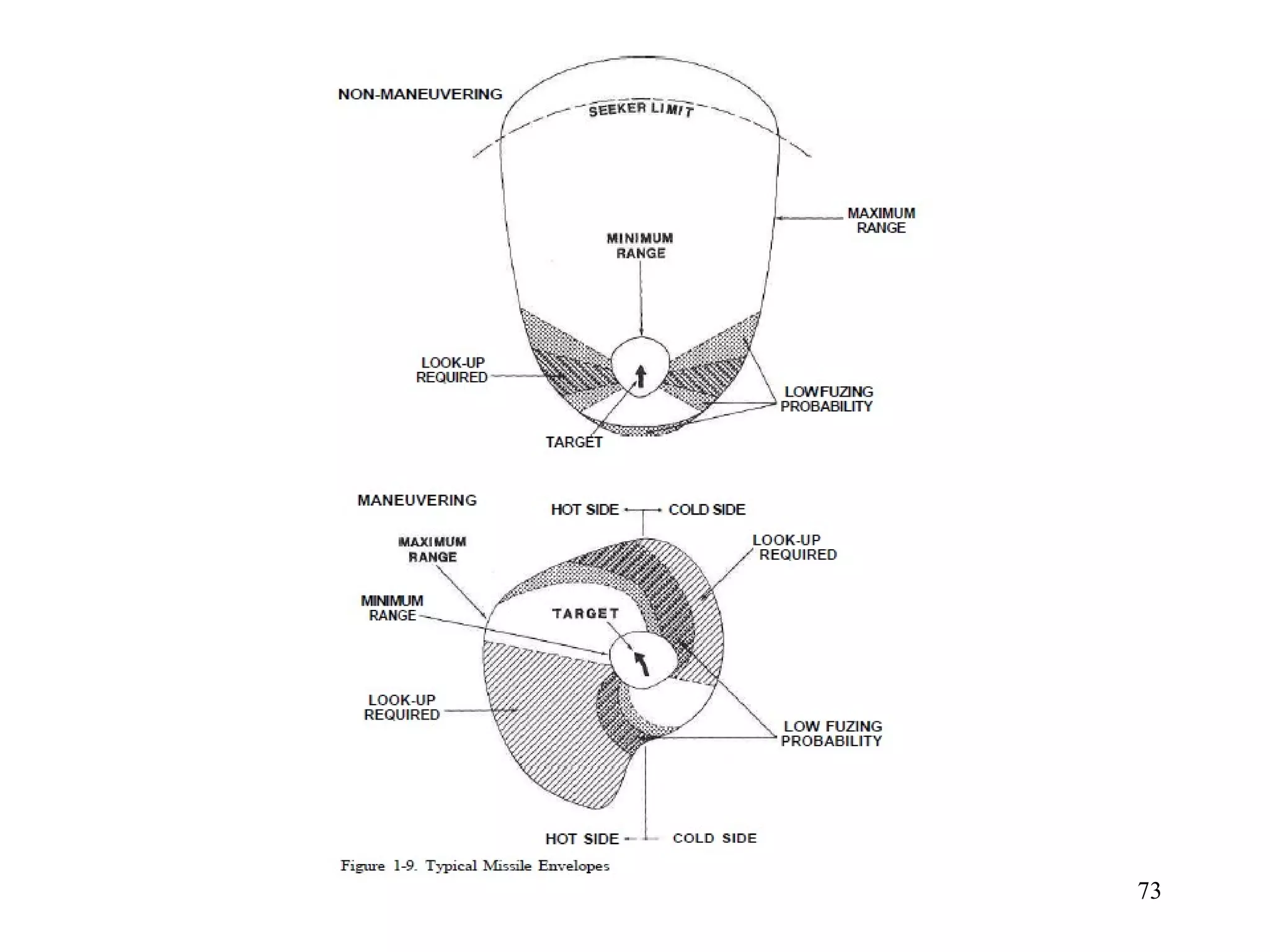
The document summarizes the history and development of gyro gunsights used in aircraft from World War 2 through the Cold War. Gyro gunsights automatically calculated the lead angle and bullet drop needed for a pilot to hit a moving target. The first operational gyro gunsight was the British Mark I in 1941. Improved models like the Mark II saw widespread use through the end of WWII. Germany developed the EZ 42 gyro sight but it did not see full deployment. The US developed the AN/ASG-26 for the F-4 Phantom, which provided targeting information via a head-up display.

Embed presentation

Downloaded 391 times
Computing Gunsight Head Up Displays& Head Mounted Displays SOLO HERMELIN Updated: 01.12.12 1
Table of Content SOLO 2 Computing Gunsight
Introduction SOLO 3 Computing Gunsight The basic material of this document was prepared between 1972 – 1973, when, as a part of my duty as an IAF Officer, was the Maintenance of Lead Computing Optical Sight Sensor (LCOSS) ASG-22, and ASG-26, Gyro Gunsight, of the F4 Phantom. The task of the LCOSS was to help the pilot to point the Aircraft Fixed Gun in such a way, that the fired projectiles will intercept the flying Target.
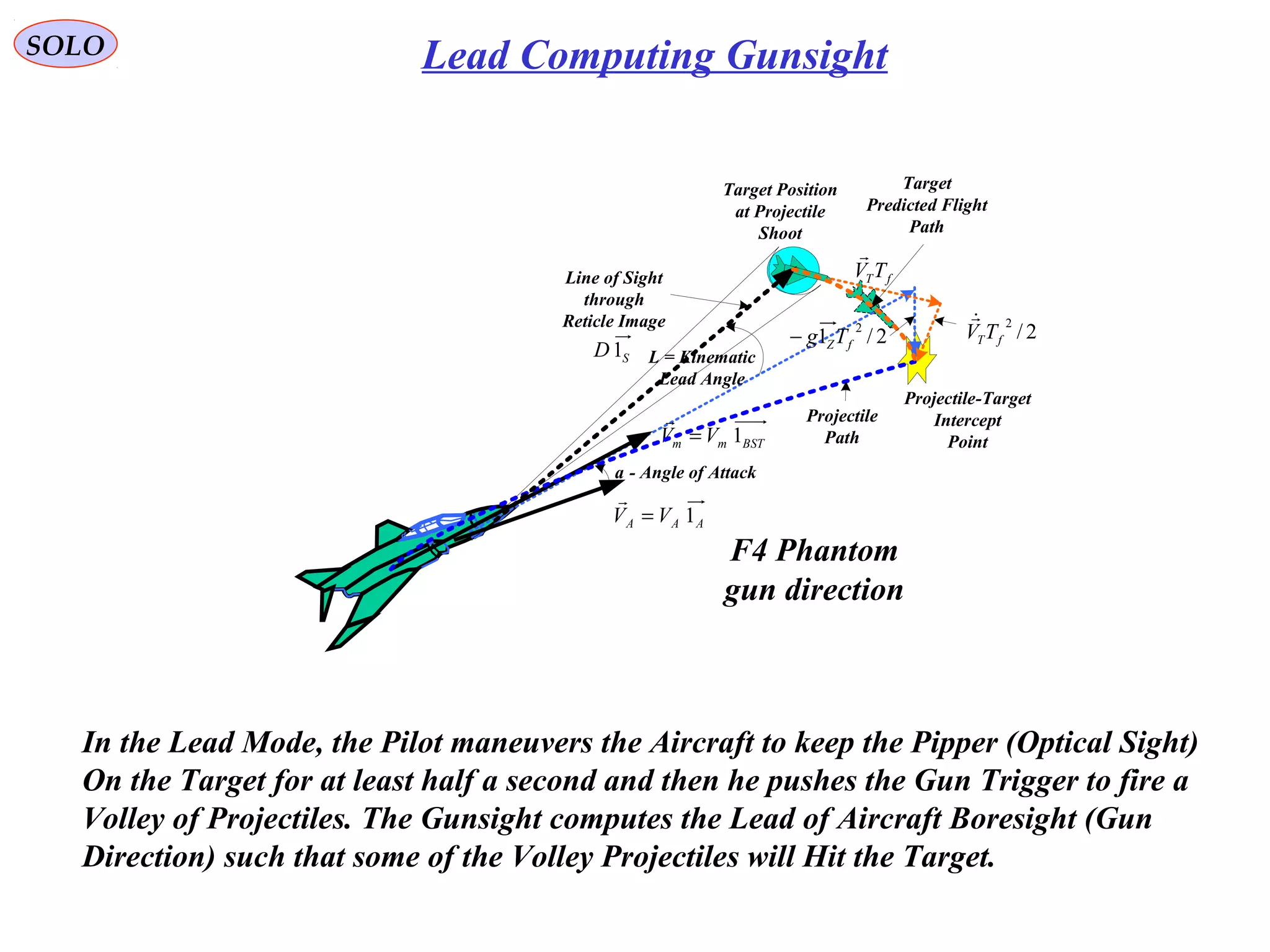
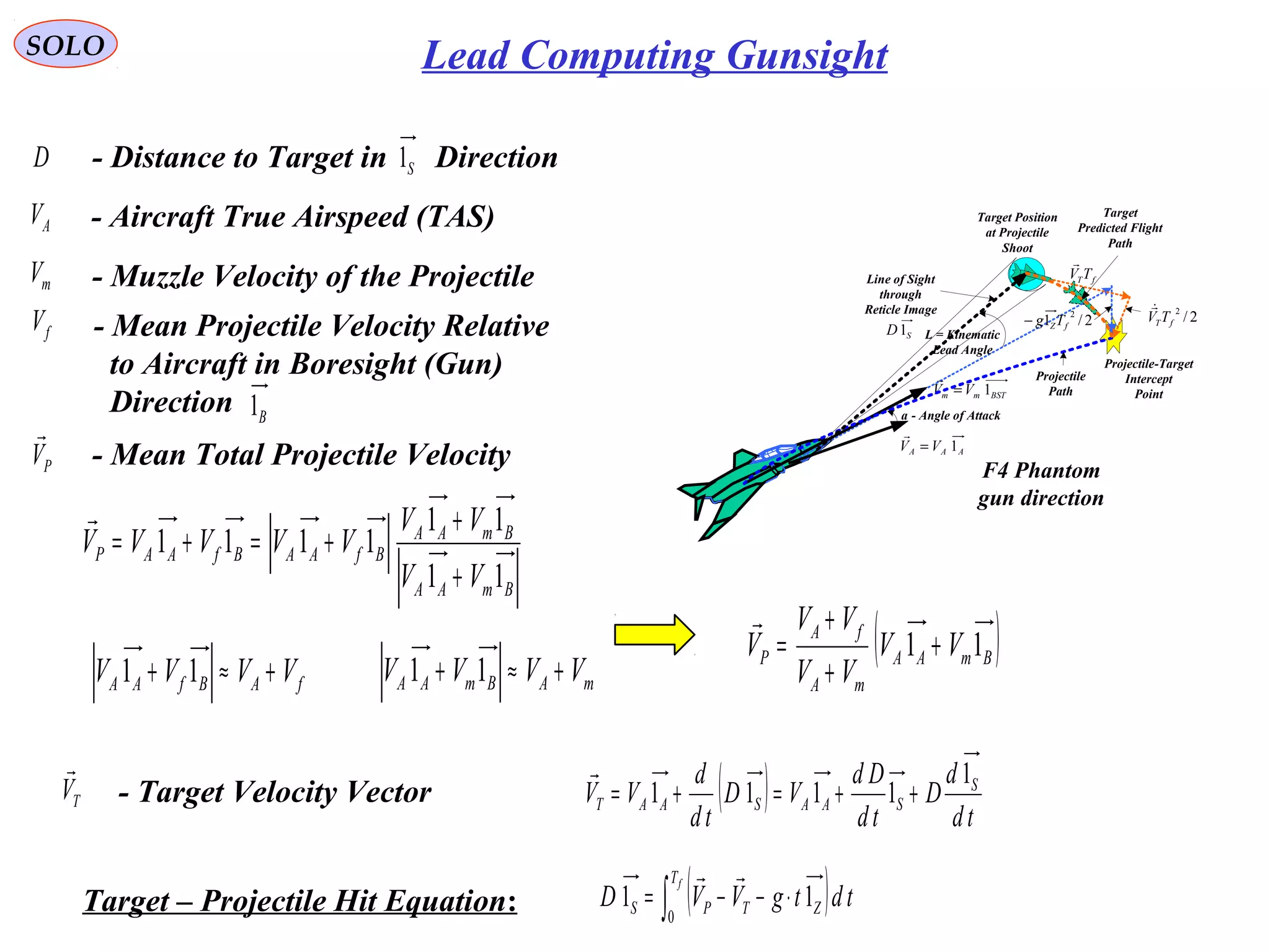
SOLO Lead Computing Gunsight A gyro gunsight (G.G.S.) is a modification of the non-magnifying reflector sight in which target lead (the amount of aim-off in front of a moving target) and bullet drop are allowed for automatically, the sight incorporating a gyroscopic mechanism that computes the necessary deflections required to ensure a hit on the target. The sight was developed just before the Second World War for aircraft use during aerial combat. Gyro Gunsight (G.G.S.) The Ferranti Gyro Sight Mk IIc Gyro gunsights were (for the most part) modifications of the reflector gunsight to aid pilots in hitting targets (other aircraft) that were turning rapidly in front of them. The reflector sight (first used on German fighters in 1918[1] and widely adopted on all kinds of fighter and bomber aircraft in the 1930s) was an optical device consisting of a 45 degree angle glass beam splitter that sat in front of the pilot and projected an illuminated image of an aiming reticule that appeared to sit out in front of the pilot's field of view at infinity and was perfectly aligned with the plane's guns ("boresighted" with the guns). The optical nature of the reflector sight meant it was possible to feed other information into field of view, such as modifications of the aiming point due to deflection determined by input from a gyroscope.[2] It is important to note that the information presented to the pilot was of his own aircraft, that is the deflection/lead calculated was based on his own bank-level, rate of turn, airspeed etc. The assumption was that the flight-path was following the flight-path of the target aircraft, as in a dogfight, therefore the input data was close-enough History Optical system of Gyro Sight
SOLO Lead Computing Gunsight Gyro Gunsight (G.G.S.) History (continue – 1) After tests with two experimental gyro gunsights which had begun in 1939, the first production gyro gunsight was the British Mark I Gyro Sight , developed at Farnborough in 1941. To save time in development the sight was based on the already existing type G prismatic sight, basically a telescopic gun sight folded into a shorter length by a series of prisms.[3] Prototypes were tested in a Supermarine Spitfire and the turret of a Boulton Paul Defiant in the early part of that year. With the successful conclusion of these tests the sight was put into production by Ferranti, the first limited-production versions being available by the spring of 1941, with the sights being first used operationally against Luftwaffe raids on Britain in July the same year. The Mark I sight had a number of drawbacks however, including a limited field of view, erratic behavior of the reticle, and requiring the pilot/gunner to put their eye up against an eyepiece during violent maneuvers. Production of the Mark I was postponed and work started on an improved sight. Changes involved incorporating the gyro adjusted reticle into a more standard reflector sight system. This new sight became the Mark II Gyro Sight, which was first tested in late 1943 with production examples becoming available later in the same year. In the Mark II the pilot had to set the wingspan of the target, and use a throttle mounted control to keep the target centered British Developments The Mark II was also subsequently produced in the US by Sperry as the K-14 (USAAF) and Mk18 (Navy) The radar-aimed AGLT Village Inn tail turret incorporated a Mark II Gyro Sight and this turret was fitted to some Lancaster bombers towards the end of World War II.
SOLO Lead Computing Gunsight Gyro Gunsight (G.G.S.) History (continue – 2) Mark II Gyro Sight demonstration on the Spitfire The Mark II Gyro Gunsight was the first gyroscopic gunsight to see widespread service with the RAF. It was first tested in late 1943 with production examples becoming available later in the same year. The Mark II was also subsequently produced in the United States as the K-14 (USAAF) and Mk18 (Navy). Spitfire Mk.IX gyro sight trial, Il-2 Sturmovik _46, Movie
SOLO Lead Computing Gunsight Gyro Gunsight (G.G.S.) History (continue – 3) German Developments Although since 1935 the relevant German companies offered the Reich Air Ministry (RLM) a new type of gyro- stabilized sight, the well-proven REVI (Reflexvisier, or reflector sight) remained in service for combat aircraft. The gyro-stabilized sights received an additional designation of EZ (Einheitszielvorrichtung, or Target Predictor Units), such as EZ/REVI-6a. The development of the EZ 40 gyro sight began in 1935 at the Carl Zeiss and Askania companies, but was of low priority. Not until the beginning of 1942, when a US P-47 Thunderbolt fighter equipped with a gyro-stabilised sight was captured, did the RLM speed up research. In the summer of 1941, the EZ 40, for which both the Carl Zeiss and Askania companies were submitting their developments, was rejected. Tested in a Bf 109 F, Askania's EZ 40 produced 50 to 100% higher hit probability compared to the then standard sight, the REVI C12c.[5] In the summer of 1943 an example of the EZ 41 developed by the Zeiss company was tested, but was refused because of too many faults. In the summer 1942, the Askania company began work on the EZ 42, which gunsight could be adjusted for the target's wingspan (in order to estimate distance to the target). Three examples of the first series of 33 pieces were delivered in July 1944. These were followed by further 770 units, the last being delivered by the beginning of March 1945. Each unit took 130 labour hours to produce. The EZ 42 was made up by two major parts, and lead computation was provided by two gyroscopes. The system, weighing 13.6 kg (30 lb) complete, of which the reflector sight was 3.2 kg, was ordered into mass production at the Steinheil company in Munich. Approximately 200 of the sights were installed into Fw 190 and Me 262 fighters for field testing. The pilots reported that attacks from 20 degrees deflection were possible, and that although the maximum range of the EZ 42 was stated as approximately 1,000 meters, several enemy aircraft were shot down from a combat distance of 1,500 meters.[6] The EZ 42 was compared with the Allied G.G.S. captured from in a P-47 Thunderbolt in September 1944 in Germany. Both sights were tested in the same Fw 190, and by the same pilot. The conclusion was critical of the moving graticule of the G.G.S., which could be obscured by the target. Compared to the EZ 42, the Allied sight's prediction angle was found on average to be 20% less accurate, and vary by 1% per degree. Tracking accuracy with the G.G.S. measured as the mean error of the best 50% of pictures was 20% worse than with the EZ 42 The German [HD], Movie
SOLO 8 Lead Computing Gunsight Lockheed Martin has developed from its earlier equipment an improved lead- computing optical sight that enables air-to-air combat to be conducted without the need for continuous target tracking. This capability is incorporated in the system for the US Air Force McDonnell Douglas F-4E.The AN/ASG-26A comprises a head-up display, two-axis lead-computing gyroscope, gyro mount and lead- computing amplifier. For airborne targets the system displays gun and missile fire- control information by means of a servoed aiming mark. Against ground targets the pilot adjusts the aiming mark manually to control gun, rocket and bombing displays.The aircraft's own manoeuvres generate rate and acceleration signals in the gyro lead-computer. Range to target is measured by radar, and angle of attack, air density and the airspeed needed for trajectory correction are supplied by the air data computer. With these parameters fed into the system, the aiming reference is displaced so as to produce the appropriate lead angle and gravity corrections. Analogues of roll angle and range are also projected onto the combining glass. In ground attack modes other sensors generate corrections for drift and offset bombing is also possible AN/ASG-26A Lead-computing optical sight (United States), FLIGHT/MISSION MANAGEMENT (FM/MM) AND DISPLAY SYSTEMS Operational status In service in the McDonnell Douglas F-4E, but no longer in production.
SOLO Lead Computing Gunsight F4 Phantom gun direction AAA VV 1=  BSTmm VV 1=  L = Kinematic Lead Angle Projectile Path Target Position at Projectile Shoot Target Predicted Flight Path Projectile-Target Intercept Point fTTV  a - Angle of Attack Line of Sight through Reticle Image SD1 2/ 2 fTTV  2/1 2 fZTg− In the Lead Mode, the Pilot maneuvers the Aircraft to keep the Pipper (Optical Sight) On the Target for at least half a second and then he pushes the Gun Trigger to fire a Volley of Projectiles. The Gunsight computes the Lead of Aircraft Boresight (Gun Direction) such that some of the Volley Projectiles will Hit the Target.
SOLO Lead Computing Gunsight AV - Aircraft True Airspeed (TAS) mV - Muzzle Velocity of the Projectile PV  - Mean Total Projectile Velocity BmAA BmAA BfAABfAAP VV VV VVVVV 11 11 1111 + + +=+=  fV - Mean Projectile Velocity Relative to Aircraft in Boresight (Gun) Direction B1 fABfAA VVVV +≈+ 11 mABmAA VVVV +≈+ 11 ( )BmAA mA fA P VV VV VV V 11 + + + =  - Distance to Target in DirectionD S1 - Target Velocity VectorTV  ( ) td d D td Dd VD td d VV S SAASAAT 1 1111 ++=+=  Target – Projectile Hit Equation: ( )∫ ⋅−−= fT ZTPS tdtgVVD 0 11  F4 Phantom gun direction AAA VV 1=  BSTmm VV 1=  L = Kinematic Lead Angle Projectile Path Target Position at Projectile Shoot Target Predicted Flight Path Projectile-Target Intercept Point fTTV  a - Angle of Attack Line of Sight through Reticle Image SD1 2/ 2 fTTV  2/1 2 fZTg−
SOLO Lead Computing Gunsight ( )BmAA Am Af P VV VV VV V 11 + + + =  - Target Velocity VectorTV  ( ) td d D td Dd VD td d VV S SAASAAT 1 1111 ++=+=  Target – Projectile Hit Equation: ( )∫ ⋅−−= fT ZTPS tdtgVVD 0 11  PV  - Mean Total Projectile Velocity ( ) ( ) ( )∫ ∫ ∫ ∫       ⋅−−−− + − +=       ⋅−−− + ⋅−⋅−⋅+⋅ +− + − =       ⋅−−− + + + + − −=       ⋅−−−−+ + + = f f f f T ZSSABA Am fm Bf T ZSSB Am fAmAmAmf ABA Am fm T ZSSBm Am Af AA Am fm T ZSSABmAA mA fA S tdtgDDV VV VV V tdtgDD VV VVVVVVVV V VV VV tdtgDDV VV VV V VV VV tdtgDDVVV VV VV D 0 0 0 0 111111 111111 11111 111111          Assuming that Tf is small and all the expressions in the integral are constant, we obtain: ( ) Z f SfSfABfA Am fm BffS T gTDTDTV VV VV TVD 1 2 111111 2 ⋅−−−− + − +=   F4 Phantom gun direction AAA VV 1=  BSTmm VV 1=  L = Kinematic Lead Angle Projectile Path Target Position at Projectile Shoot Target Predicted Flight Path Projectile-Target Intercept Point fTTV  a - Angle of Attack Line of Sight through Reticle Image SD1 2/ 2 fTTV  2/1 2 fZTg−
SOLO Lead Computing Gunsight Target – Projectile Hit Equation: ( ) Z f SfSfABfA Am fm BffS T gTDTDTV VV VV TVD 1 2 111111 2 ⋅−−−− + − +=   Let multiply this equation by (vector product)×S1 ( ) ZS f SSfSSfABSfA Am fm BSffSS T gTDTDTV VV VV TVD 11 2 11111111111 2 00 ×⋅−×−×−−× + − +×=×      Since defineLLSB ≈=× sin11 LSB  =× :11 Define the Line-of-Sight Rate.SS 11:  ×=Λ ( ) ( )( ) ( )( ) αα ≈−⋅≈−⋅−=−× ABSABSABABS 11,1sin11,1sin11111We have Define ( ) α  =−× :111 ABS ZS f ffA Am fm ff T gTDTV VV VV LTV 11 2 0 2 ×⋅−Λ− + − +−=  αWe obtain ZS f f f A Am fm f V Tg V V VV VV V D L 11 2 × ⋅ ⋅ −⋅ + − +Λ−= α  or F4 Phantom gun direction AAA VV 1=  BSTmm VV 1=  L = Kinematic Lead Angle Projectile Path Target Position at Projectile Shoot Target Predicted Flight Path Projectile-Target Intercept Point fTTV  a - Angle of Attack Line of Sight through Reticle Image SD1 2/ 2 fTTV  2/1 2 fZTg−
SOLO Lead Computing Gunsight Target – Projectile Hit Equation: ZS f f f A Am fm f V Tg V V VV VV V D L 11 2 × ⋅ ⋅ −⋅ + − +Λ−= α  Assume a Coordinated Turn of the Aircraft ay a constant True Airspeed Va: ZNtotal gaa 1−=  where is the acceleration normal (to Aircraft Wing Plan) Na  ( )  AAAAAAtot VVV td d a 111 0    +== ≈ ( ) NANSANAANtotalZ asVaVsaVsaassg  ×−Λ=     −×≈     −×=−×=×− 11111111 NAZ asVsg  ×−Λ≈×− 111 N f f f fA ZS f f as V T V TV V Tg  × ⋅ −Λ ⋅ ⋅ ≈× ⋅ ⋅ − 1 22 11 2 NS f f f A Am fmfA f a V T V V VV VV D TV V D L  × ⋅ −⋅ + − +Λ⋅      ⋅ ⋅ −⋅−= 1 22 1 α F4 Phantom gun direction AAA VV 1=  BSTmm VV 1=  L = Kinematic Lead Angle Projectile Path Target Position at Projectile Shoot Target Predicted Flight Path Projectile-Target Intercept Point fTTV  a - Angle of Attack Line of Sight through Reticle Image SD1 2/ 2 fTTV  2/1 2 fZTg−
SOLO Lead Computing Gunsight VR VC M S V D = ⋅ ⋅ −=   2 2 1 ρ Computation of Time of Flight Tf and Vf: Assume mP, mass of projectile, and CD , the drag coefficient, assumed constant from which VC M S Rd Vd D⋅ ⋅ −= ρ 2 1 RdC M S V Vd D⋅ ⋅ −= ρ 2 1 RC M S V V D I ⋅ ⋅ −= ρ 2 1 ln ( ) RC M S mA RC M S I DD eVVeVV ⋅ ⋅ −⋅ ⋅ − +== ρρ 2 1 2 1 ( ) ( ) DB DK fB mA DC m S fD mA D RC m S f mA D f avg C m S K e DK VV e DCS mVV Rde D VV RdV D V fB fDf Df ⋅= −⋅ ⋅⋅ + =        −⋅ ⋅⋅⋅ ⋅+⋅ = + == −⋅ ⋅ −⋅ ⋅ − ∫∫ 2 1 : 11 21 2 1 0 2 1 0 ρ ρρ ρρ ( ) ( ) ( ) fmABmAfBfB fB mA A DK fB mA Aavgf DVVKVVDKDK DK VV Ve DK VV VVV fB ⋅+⋅⋅⋅−≈−      +⋅⋅⋅−⋅⋅+−⋅ ⋅⋅ + ≈−−⋅ ⋅⋅ + =−= − ρρρ ρρ ρ 2 1 2 1 111: 2 
SOLO Lead Computing Gunsight Computation of Time of Flight Tf and Vf (continue – 1) ( ) fmABmAavgf DVVKVVVV ⋅+⋅⋅⋅−≈−= ρ 2 1 : ( ) ∫∫ +=+= ff T TS T Zf tdVDtdgVD 00 11  ( ) ffAfavg T f TVVTVtdVD f ⋅+=⋅=≈ ∫0  ( ) fA T SSA T TSf TDVDtdDDVDtdVDD ff ⋅++≈     +++≈+= ∫∫    00 111 ( ) ( ) ( ) 0=−⋅−⇒⋅++≈⋅+≈ DTDVTDVDTVVD fffAffAf  ( ) ( )[ ] 0 2 1 =−⋅           −⋅++⋅+⋅⋅⋅− DTDTDVDVVKV f D fAmABm f     ρ
SOLO Lead Computing Gunsight Computation of Time of Flight Tf and Vf (continue – 2) ( ) ( )[ ] 0 2 1 =−⋅               −⋅++⋅+⋅⋅⋅− DTDTDVDVVKV f V D fAmABm f f        ρ ( ) ( ) ( ) 0 2 1 2 1 2 =+⋅      +⋅⋅⋅−−⋅+⋅+⋅⋅⋅ DTVVKVTDVVVK f B mABmf A AmAB       ρρ A DABB Tf ⋅ ⋅⋅−− = 2 42 ff TDDV /+= 
SOLO Snap Shot Gunsight In the Lead Mode of Fire, the Pilot must keep the Pipper on the Target, for a small period of time, and then he starts firing the Gun. In the Snap Shoot Mode of Fire, the Pilot must bring the Pipper to cross the Target, but must start Firing at least Time of Flight (Tf ) (no more then a second), before Target Crossing. This Mode will work if the Pipper points on the Projectile Position Tf seconds after Firing, so the Projectile (fired Tf before), the Pipper and the Target coincide. The Tf is given as before by the three equations: ( ) ( ) ( )         =−⋅− ⋅++≈ ⋅+⋅⋅⋅−≈−= 0 2 1 : DTDV TDVDD DVVKVVVV ff fAf fmABmAavgf   ρ A DABB Tf ⋅ ⋅⋅−− = 2 42 ( ) ( ) ( ) 0 2 1 2 1 2 =+⋅      +⋅⋅⋅−−⋅+⋅+⋅⋅⋅ DTVVKVTDVVVK f B mABmf A AmAB       ρρ Tf is not a function of Target Data, therefore the Pipper doesn’t have to be on Target to
SOLO Snap Shot Gunsight In the Snap Shot Mode of Fire, the Pipper is pointed to the Projectile that was fired Tf seconds before. - unit vector given Pipper Direction at Fire.S1  fS1  - unit vector given Pipper Direction at Tf. ∫+= f f T SSS td 0 111  During Tf the Aircraft Position, relative to Projectile Firing is. ( )∫       + fT AAAA tdV td d tV 0 11  Snap Shoot Gunsight Equation is: ( ) ff fff SS T AAPZ TT P KtdV td d tVtdtgtdV 111 000  =      +−− ∫∫∫ ( )         +=      −−− ∫∫ f f f T SSS T AAZAP tdKtdV td d ttgVV 00 1111  or:
SOLO Snap Shot Gunsight In the Snap Shot Mode of Fire, the Pipper is pointed to the Projectile that was fired Tf seconds before (continue – 1). ( )         +=      −−− ∫∫ f f f T SSS T AAZAP tdKtdV td d ttgVV 00 1111  ( )  ZNAAAAAAtotal gaVVV td d a 1111 0 −=+== ≈    SS T SSNAP f f f KtdKatVV 11 0  =     −−−∫ As a First Order Assumption, all the vectors in the previous equation, we obtain: SSfSSfNAfAfP ff KTKTaTVTV 112/1 2  =−−− ( )BmAA mA fA P VV VV VV V 11 + + + =  SSfSSfNAA Am fm Bm Am Af ff KTKTaV VV VV V VV VV 112/11  =⋅      −− + − − + +
   SOLO Snap Shot Gunsight   In the Snap Shot Mode of Fire, the Pipper is pointed to the Projectile that was fired Tf seconds before (continue – 2). SSfSS f NAA Am fm Bm Am Af ff KTK T aV VV VV V VV VV 11 2 11  =⋅      −− + − − + + 01111 2 11111  =×=⋅      ×−×−× + − −× + + SSSfSSS f NSASA Am fm BSm Am Af ff KTK T aV VV VV V VV VV   Multiply (Vector Product) this equation by from the Left: S1    We defined: ( ) α α     −−=×⇒     =−× −=× Λ=× L L AS ABS BS SS 11 :111 :11 :11 ( ) 0 2 1  =Λ−×−−− + − − + + − fS f NSA Am fm m Am Af K T aLV VV VV LV VV VV α 0 2 1  =Λ−×− + − +− fS f NSA Am fm f K T aV VV VV LV α ×S1 
   SOLO Snap Shot Gunsight   In the Snap Shot Mode of Fire, the Pipper is pointed to the Projectile that was fired Tf seconds before (continue – 3). ( ) 01 2  =Λ−× ⋅ − + − = f S NS f f f A Am fm V K a V T V V VV VV L f α   Let compute            .fSK From the Figure ( )   N ff a Z f SSAfAfp ga T KTVTV 1 2 11 2 +++= fffff SfASSAfAN f SSAfAfpfp KTVKTVa T KTVTVTV +≈+≈++== 11 2 11 2  But we found also that ffAfp TVVTV += Therefore                                   andffS TVK f = ( )NS f f f A Am fm f a V T V V VV VV TL  ×− + − +Λ−= 1 2 α
   SOLO Computing Gunsight We obtained ( )NS f f f A Am fm f a V T V V VV VV TL  ×− + − +Λ−= 1 2 α NS f f f A Am fmfA f a V T V V VV VV D TV V D L  × ⋅ −⋅ + − +Λ⋅      ⋅ ⋅ −⋅−= 1 22 1 α Lead Computing Snap Shot Computing We can see that the two expression are different only in the first term, and we can write            ⋅ ⋅ −⋅ =× ⋅ −⋅ + − +Λ⋅−= ShootSnapT Lead D TV V D Ka V T V V VV VV KL f fA fNS f f f A Am fm 2 1 1 2  α Note: The Pilot can use a Snap Shot Gunsight in Lead Mode, since by keeping the Pipper on the Target and Firing for at leas Tf seconds (around a second) the Projectiles will Hit the Target.
   SOLO Lead Computing Gunsight Gyro Gunsight (G.G.S.)  A Gyro Gunsight (G.G.S.) is composed of a Gimbaled Dwo Degrees of Freedom  Gyro, that Rotation Axis points,  when the Aircraft isn’t move, in the Boresight Direction  (also Gun direction). •  The Optical Pipper of the Gunsight  is Slaved to     Gyro direction.  •  In front of the Gyro’s Rotor  is a Metallic Disc that     rotates with it. •  In front of the Metallic Rotating Disc is a Static    Electromagnet. The Electromagnetic Field is pointed     in the Boresight Direction. It’s Strength is defined    by a Current controlled by an Analog Lead Gunsight    Computer. • Due to Rotation of the Disc in an Electromagnetic Field, Eddie Currents are   induced in the Disc Metallic Surface. • When the Aicraft Maneuvers, the Boresight Direction will change and the     Eddie Currents will move, relative to Electromagnetic Field, causing an    Electromagnetic Force acting on the Disc, therefore a Moment on the    Gimbaled Gyro.  •  By applying Electromagnet’s Current to satisfy the Lead Angle Equation the Gyro will    point in the required direction, and so the Optical Pipper.            ⋅ ⋅ −⋅ =× ⋅ −⋅ + − +Λ⋅−= SnapShootT Lead D TV V D Ka V T V V VV VV KL f fA fNS f f f A Am fm 2 1 1 2  α
   SOLO Lead Computing Gunsight Gyro Gunsight (G.G.S.) 
   SOLO Lead Computing Gunsight Gyro Gunsight (G.G.S.)   Torque of the Eddie Currents The Gyro’s Metallic Disk rotates in front of the  Electromagnet Field. This produces Eddie Currents on the Disk Skin. As long as the Gyro Rotation Direction        is the same as Electromagnetic Field Direction          the Moment due to Eddie Currents in the Electromagnetic Field  B is zero. When the  Aircraft maneuvers ( and       relative to      ) the  Moment due to Eddie Currents is not zero, and this in turn, will change the Gyro direction        . We want to find the relation between the  Electromagnetic Field Intensity B, the position of        and       , and the Torque on the Gyro. S1 B1 B1 S1 S1 B1 S1
   SOLO Lead Computing Gunsight Gyro Gunsight (G.G.S.)   Suppose a small surface of the Rotating Disk (ω), at a distance R from the center of Gyro  Gimbal, moving at the velocity u.  The Electromagnetic Field Intensity Vector BEMB IkBB 11 −=−=  ( ) ( ) rSrS RRu 1111 ×−=×−= ωω   Because of the Electromagnetic Field B  the free electrons in the Metallic Disk will Move, and produce an Electric Field Intensity BuE  ×=  This will create a Current Intensity in the  Disk Skin BuEj  ×== ρρ 11  where ρ is the resistance mean value.  Torque of the Eddie Currents (continue – 1)
   SOLO Lead Computing Gunsight Gyro Gunsight (G.G.S.)  The Current in the skin surface dS is  The force acting on the Current of length dl  due to the Electromagnetic Field B is SkinSdBuSdjid  ×== ρ 1  Torque of the Eddie Currents (continue – 2) ( )   SkinVd Skin ldSdBBuldBidfd ××=×= ρ 1 ( ) ( ) 22 0 BuBuBuBBBu    −=−⋅=×× SkinVdu B fd  ρ 2 −= The Moment on the Gyro is computed by  considering the distance from the Center of Gyro  Gimbals. ( ) SkinrSr Skinrr VdR BR Vdu BR fdRTd 111 11 2 2 ×−×−= ×−=×= ω ρ ρ 
   SOLO Lead Computing Gunsight Gyro Gunsight (G.G.S.)   Torque of the Eddie Currents (continue – 3) ( ) SkinrSr Vd BR Td 111 22 ××= ρ ω ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )[ ] ( ) ( ) ( ) ( ) ( ) ( )rSSrSrSSrSr rSSrS rrSSrSrSSrSrS rSrSrS rSrSrSr 111111111111 11111 11111111111111 1111111 1111111 2 2 2 ××⋅+     ⋅−=×× ××⋅= −⋅⋅=     ⋅−−⋅− ⋅−=××⋅ ⋅−=××  Decompose this in the component in       direction  (that will be compensate by the Gyro Motor) and  that normal to it (that will cause the precession). S1 ( ) ( ) ( )        nSS Td SkinrSSrS Td SkinrSS Vd BR Vd BR Td 111111111 22222 ××⋅+     ⋅−= ρ ω ρ ω
   SOLO Computing Gunsight Gyro Gunsight (G.G.S.)   Torque of the Eddie Currents (continue – 4)  The Total Moment normal to Gyro Rotation Axis is ( ) ( ) ( )BSSCG V SkinrSSrSS IK Vd BR T Skin n 111 11111 2 22 ××= ××⋅= ∫ ω ρ ω
   SOLO Computing Gunsight Gyro Gunsight (G.G.S.)             ⋅ ⋅ −⋅ =× ⋅ ⋅−⋅ + − ⋅+−=Λ ΛΛ Λ SnapShootT Lead D TV V D Ka V T KV V VV VV K L K f fA fNS f f f A Am fm 2 1 1 2 111 32 1            α Implementation of  L K  1 1 −=Λ ( )SB K L K 11 11 1  ×−=−=Λ We want to find the Torque to be applied on the  Gyro to obtain this. In steady-state ( ) SSB G S G IH S K I L K I HHT G 11111111  ××=×=×Λ−=×Λ= = ωωω ( )BSSCGS IKT n 111 2 ××= ω  We found that the Moment on the Gyro due to Eddie Currents produce by the deflection of the  Gyro direction to        relative to Electromagnet is S1 B1 Since ( ) ( ) ( )BSSSBSSSB 111111111  ××=××−=×× Equalizing the two expressions we must have 2 CG G IK K I ω ω = K KI I GG C = Implementation of Lead Computation with Gyro Gunsight
   SOLO Computing Gunsight Gyro Gunsight (G.G.S.)             ⋅ ⋅ −⋅ =× ⋅ ⋅−⋅ + − ⋅+−=Λ ΛΛ Λ SnapShootT Lead D TV V D Ka V T KV V VV VV K L K f fA fNS f f f A Am fm 2 1 1 2 111 32 1            α Implementation of  We want to find the Torque to be applied on the  Gyro to obtain this.  ( )[ ] SABSGSG K K IIT 1111122  ×−×−=×Λ−= α ωω ( )ABS K f A Am fm K K V V VV VV K 111 1 :2    −×=⋅ + − ⋅=Λ α α α ( )[ ] ( ) αωω α α α K K I K K IT GSABSG ABS =×−×= ≈−      11,1sin 2 1111 ( )ABS 111:  −×=α f A Am fm V V VV VV K ⋅ + − =:α Implementation of Lead Computation with Gyro Gunsight (continue – 1)
   SOLO Computing Gunsight Gyro Gunsight (G.G.S.)             ⋅ ⋅ −⋅ =× ⋅ ⋅−⋅ + − ⋅+−=Λ ΛΛ Λ SnapShootT Lead D TV V D Ka V T KV V VV VV K L K f fA fNS f f f A Am fm 2 1 1 2 111 32 1            α Implementation of  We want to find the Torque to be applied on the  Gyro to obtain this.  ( ) SNS f f GSG a V T K IIT 11 2 1 133  ×× ⋅ ⋅=×Λ−= ωω NS f f a V T K  × ⋅ ⋅−=Λ 1 2 1 :3 ( ) ( ) f fN G aa SNS f f G V T K a Ia V T K IT NSN ⋅ ⋅=×× ⋅ ⋅= ≈ 2 11 2 1 1,1sin 3 ωω    Implementation of Lead Computation with Gyro Gunsight (continue – 2)
   SOLO Computing Gunsight Gyro Gunsight (G.G.S.)             ⋅ ⋅ −⋅ =× ⋅ ⋅−⋅ + − ⋅+−=Λ ΛΛ Λ SnapShootT Lead D TV V D Ka V T KV V VV VV K L K f fA fNS f f f A Am fm 2 1 1 2 111 32 1            α ( ) SNS f f GSG a V T K IIT 11 2 1 133  ×× ⋅ ⋅=×Λ−= ωω Implementation of Lead Computation with Gyro Gunsight (continue – 3) is perpendicular to         and in the plane defined by        and  S1  ( )AB 11  − S1  is perpendicular to         and in the plane defined by        and  S1  Na  S1  Since L and α are small angles, we may say  that          and            are collinear and in the Gyro zG direction, therefore 2T  3T  GGG Z f NfG ZZ V aT K K I TTT 1 2 132          ⋅ ⋅ +−=≈+ α ω α ( )[ ] SABSGSG K K IIT 1111122  ×−×−=×Λ−= α ωω
   SOLO Computing Gunsight Gyro Gunsight (G.G.S.)  Lead Angle Computing Loops
   SOLO Head-up Display (HUD)   A Head-Up Display or heads-up display—also known as a  HUD—is any transparent display that presents data without  requiring users to look away from their usual viewpoints. The  origin of the name stems from a pilot being able to view  information with the head positioned "up" and looking  forward, instead of angled down looking at lower instruments   A typical HUD contains three primary components: a  Projector Unit, a Combiner, and a Video Generation  Computer • The Projection Unit in a typical HUD is an optical collimator setup: a convex lens or concave  mirror with a Cathode Ray Tube, light emitting diode, or liquid crystal display at its focus. This  setup (a design that has been around since the invention of the reflector sight in 1900) produces  an image where the light is parallel i.e. perceived to be at infinity • The Combiner is typically an angled flat piece of glass (a beam splitter) located directly in front  of the viewer, that redirects the projected image from projector in such a way as to see the field of  view and the projected infinity image at the same time. Combiners may have special coatings that  reflect the monochromatic light projected onto it from the projector unit while allowing all other  wavelengths of light to pass through. In some optical layouts combiners may also have a curved  surface to refocus the image from the projector • The Computer provides the interface between the HUD (i.e. the projection unit) and the  systems/data to be displayed and generates the imagery and symbology to be displayed by the  projection unit 
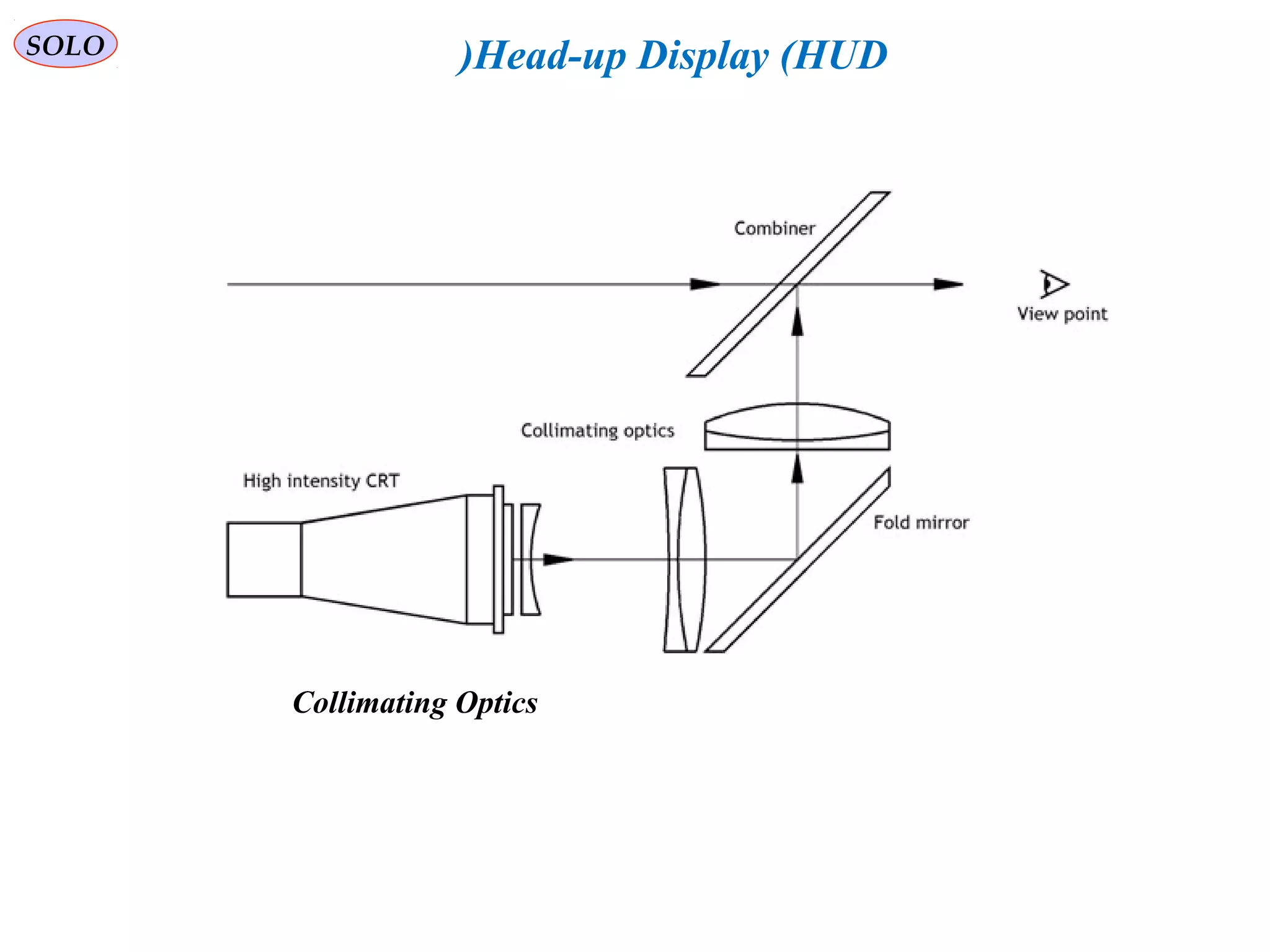
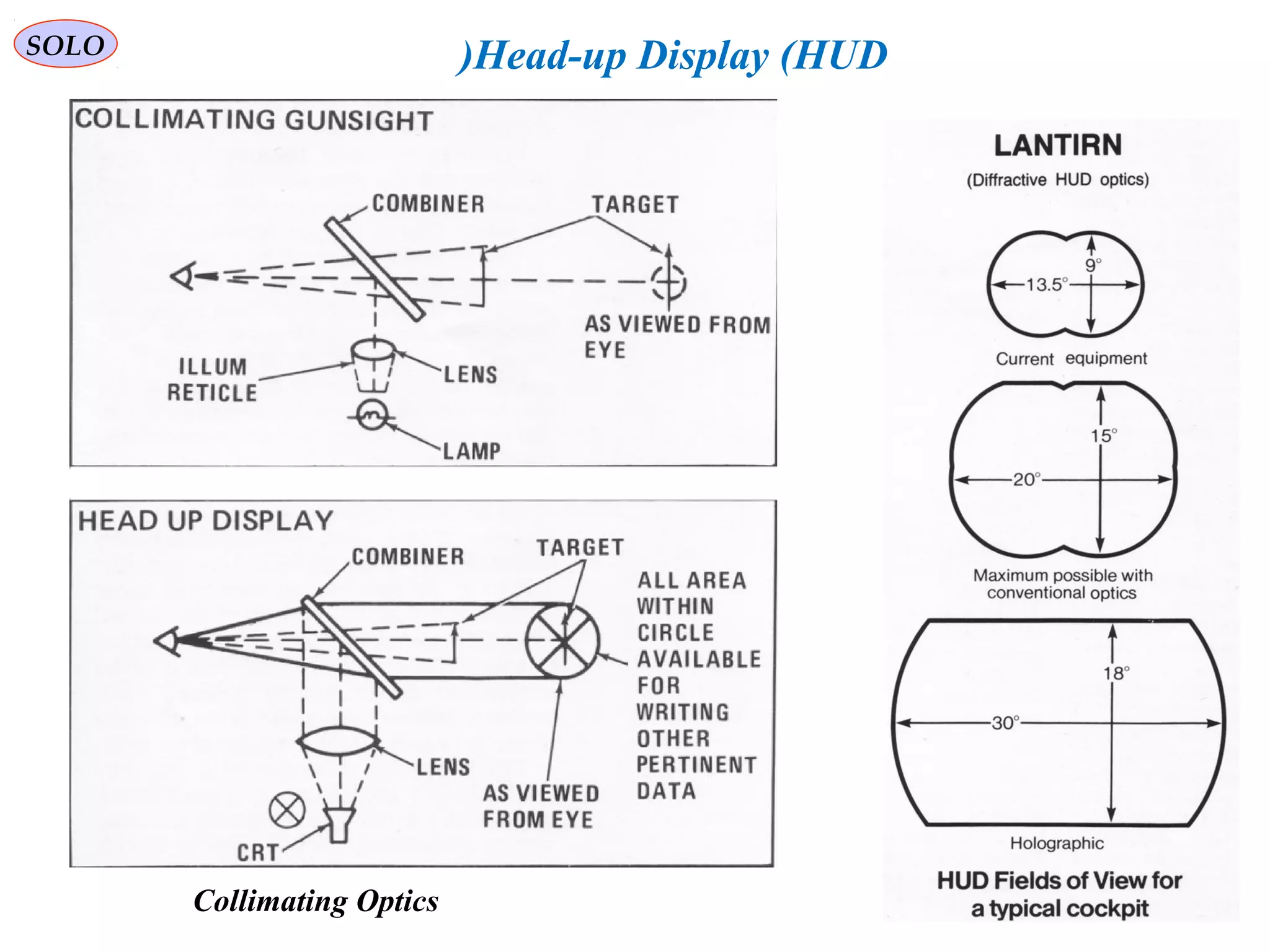
   SOLO Head-up Display (HUD) Collimating Optics
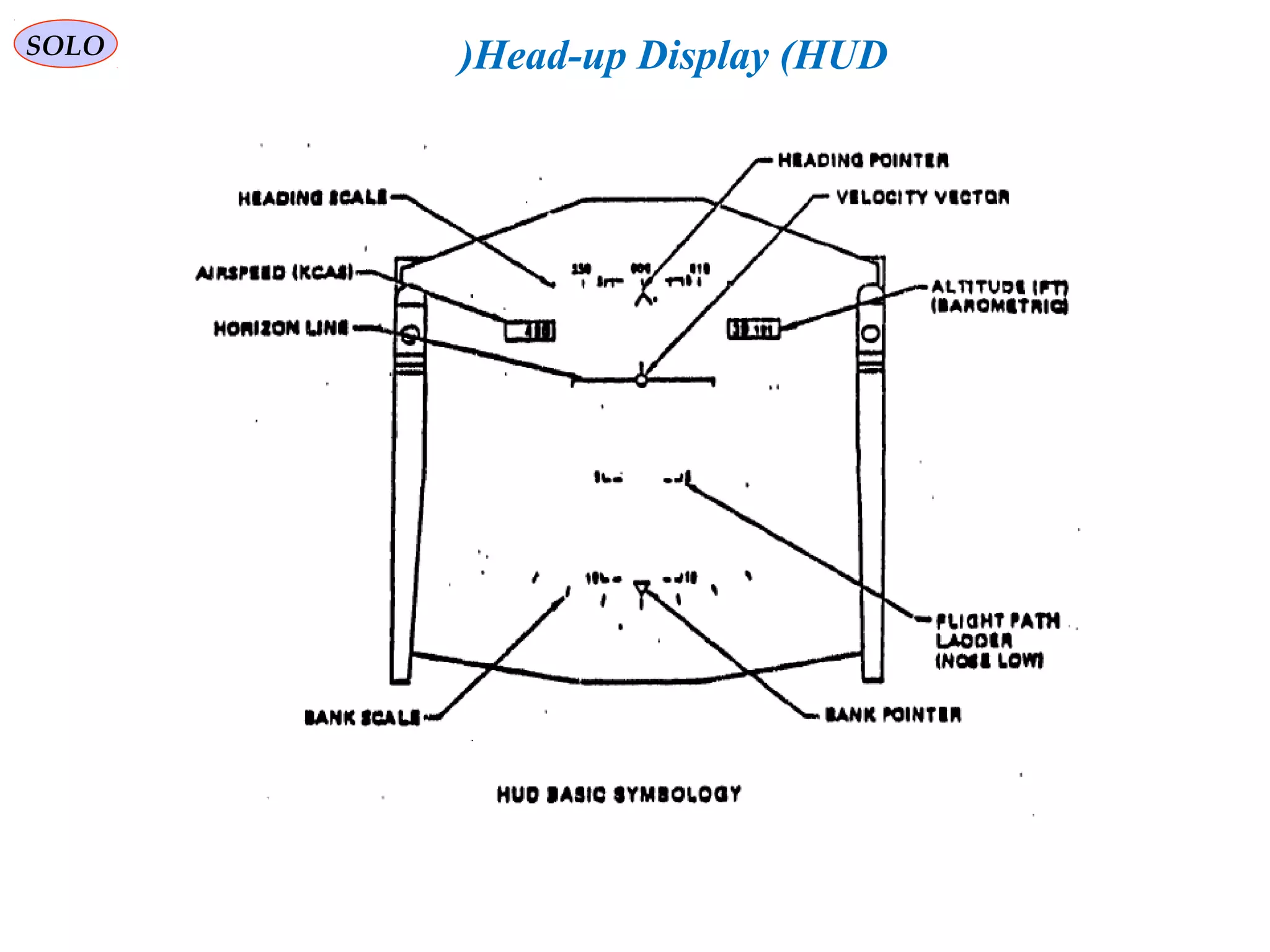
   SOLO Head-up Display (HUD) Collimating Optics
   SOLO Head-Mounted Display (HMD) Other than fixed mounted HUDs, there are also HMDs head-mounted displays.  Including Helmet Mounted Displays (both abbreviated HMD), forms of HUD that  features a display element that moves with the orientation of the users' heads. Many modern fighters (such as the F/A-18, F-16 and Eurofighter) use both a HUD  and HMD concurrently. The F-35 Lightning II was designed without a HUD, relying  solely on the HMD, making it the first modern military fighter not to have a fixed  HUD Types
   SOLO Head-up Display (HUD( HUDs are split into four generations reflecting the technology used to generate  the images. •  First Generation—Use a CRT to generate an image on a phosphor screen,  having the disadvantage of the phosphor screen coating degrading over time.  The majority of HUDs in operation today are of this type. •  Second Generation—Use a solid state light source, for example LED, which  is modulated by an LCD screen to display an image. These systems do not fade  or require the high voltages of first generation systems. These systems are on  commercial aircraft. •  Third Generation—Use optical waveguides to produce images directly in the  combiner rather than use a projection system. •  Fourth Generation—Use a scanning laser to display images and even video  imagery on a clear transparent medium. Newer micro-display imaging technologies are being introduced, including  liquid crystal display (LCD(, liquid crystal on silicon (LCoS(, digital micro- mirrors (DMD(, and organic light-emitting diode (OLED(.
   SOLO Head-up Display (HUD(
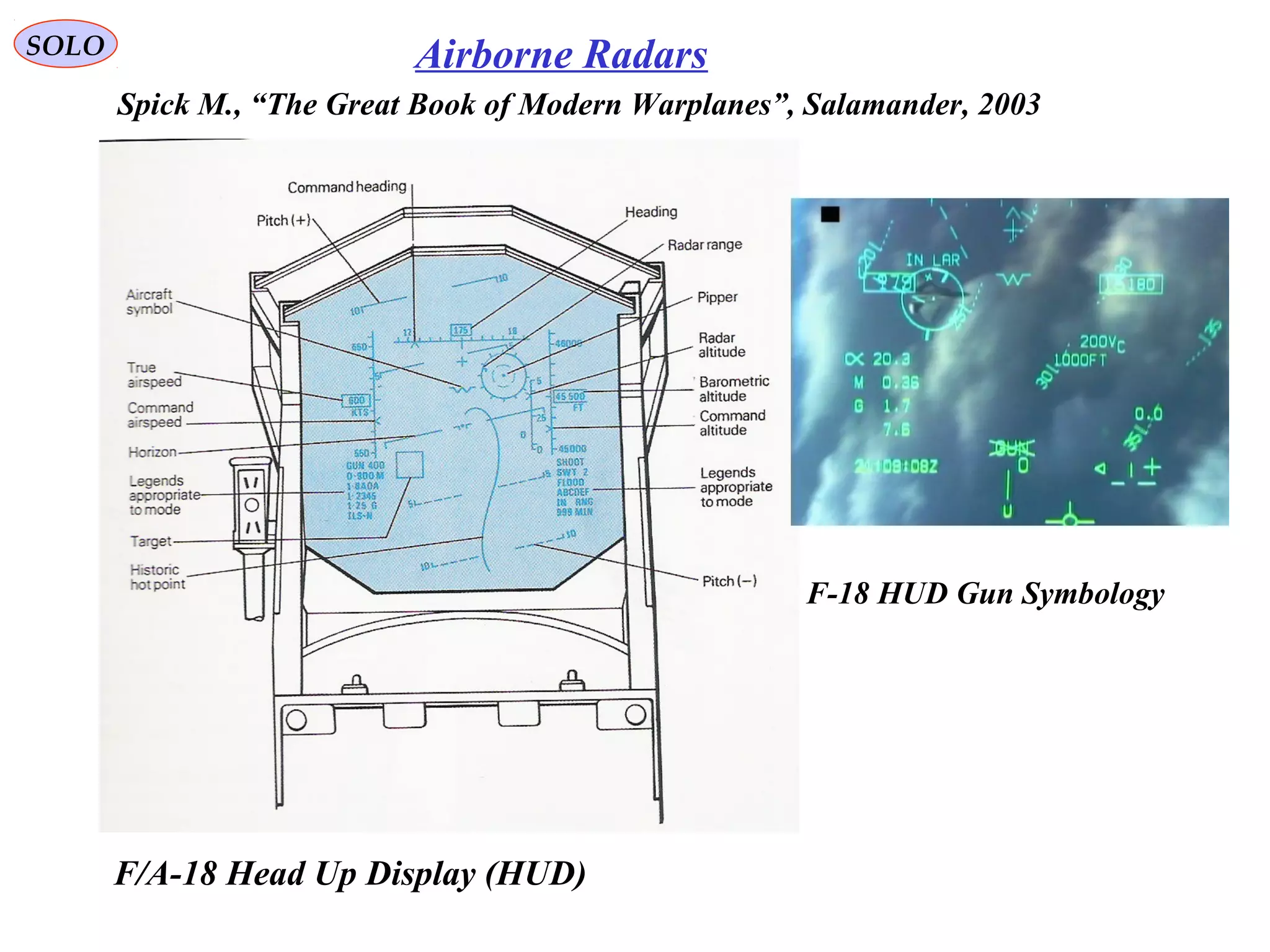
   SOLO Airborne Radars Spick M., “The Great Book of Modern Warplanes”, Salamander, 2003 F/A-18 Head Up Display (HUD( F-18 HUD Gun Symbology
42 SOLO Head-up Display (HUD(
   SOLO Head-up Display (HUD( Typical aircraft HUDs display data: Airspeed, Altitude, a Horizon Line, Heading,  Turn/Bank and Slip/Skid indicators. These instruments are the minimum required by  14 CFR Part 91. Other symbols and data are also available in some HUDs: •  Boresight or Waterline Symbol —is fixed on the display and shows where the nose  of the aircraft is actually pointing. •  Flight Path Vector (FPV( or Velocity Vector Symbol —shows where the aircraft is  actually going, the sum of all forces acting on the aircraft.]  For example, if the aircraft  is pitched up but is losing energy, then the FPV symbol will be below the horizon even  though the boresight symbol is above the horizon. During approach and landing, a  pilot can fly the approach by keeping the FPV symbol at the desired descent angle and  touchdown point on the runway. •  Acceleration Indicator or Energy Cue —typically to the left of the FPV symbol, it is  above it if the aircraft is accelerating, and below the FPV symbol if decelerating. •  Angle Of Attack indicator —shows the wing's angle relative to the airflow, often  displayed as "α". •  Navigation Data and Symbols —for approaches and landings, the flight guidance  systems can provide visual cues based on navigation aids such as an Instrument  Landing System (ILS(  or Augmented Global Positioning System such as the Wide  Area Augmentation System. Typically this is a circle which fits inside the flight path  vector symbol. Pilots can fly along the correct flight path by "flying to" the guidance  cue.
   SOLO Head-up Display (HUD( 1 Available Gs 10 Gun Cross 2 Current Gs 11 Waterline Symbol 3 Mach Ratio 12 Velocity Vector 4 True Airspeed 13 Barometric Altitude 5 Angle of Attack (AOA) 14 Radar Altitude 6 Indicated Airspeed 15 Horizon Line 7 Pitch Ladder 16 Ghost Velocity Vector 8 Command Heading Marker 17 Maximum Projected Area 9 Heading Scale F-15E  - Head-Up Display F-15C_ M61A1 Vulcan Cannon and AIM-9M Sidewinder
   SOLO Head-up Display (HUD( In addition to the generic information described above, military  applications include weapons system and sensor data such as: •  Target Designation (TD( indicator—places a cue over an air or ground  target (which is typically derived from radar or inertial navigation system  data(.  •  Vc—closing velocity with target.  •  Range—to target, waypoint, etc.  •  Launch Acceptability Region (LAR(—displays when an air-to-air or air- to-ground weapon can be successfully launched to reach a specified  target.  • Weapon Seeker or sensor line of sight—shows where a seeker or sensor  is pointing.  •  Weapon status—includes type and number of weapons selected,  available, arming, etc. Military aircraft specific applications
   SOLO Airborne Radars http://www.ausairpower.net/Profile-F-15A-D.html F-15 Head Up Display (HUD( Data at Different Mission Modes
   SOLO F16 F-16: Enhanced Envelope Gun Sight (EEGS(
   SOLO F16 F-16: Lead Computing Optical Sight (LCOS(
   SOLO F16 F-16: AIM-9 Missile Mode
   SOLO F16 F-16: AIM-120 AMRAAM Missile Mode
   SOLO F16 F16 Gunsight Four different sighting references are available for use: 1.Gun Cross 2.Lead Computing Optical Sight (LCOS( 3.Snap shot Sight (SS( 4.Enhanced Envelope Gunsight (EEGS( only for F16C and up. 1.   The Gun Cross is always available and easily used. The Pilot can effectively imagine  the Gun Cross as being where gun barrels are pointed. Proper Aim is achieved by       positioning the Gun Cross in the Target Plane of Motion (POM( with the proper  amount of Lead. The Gun Cross is a very good reference to use to initially establish  the Gun in the Target ‘s POM with some amount of lead. As Range decreases the  Pilot can refine the Lead Angle by using as reference the LCOS/EEGS Pippers  before firing. Without  EEGS the Gun Cross is the only usable reference during very  high dynamic, high aspect angle shot attempt. 2.    The LCOS Pipper represents a Sighting Reference for which the Gun is now  properly aimed.  With the Pipper. Pipper helps the Pilot to establish th proper Lead  Angle to kill  the Target. The key LCOS assumption is that the Pilot is tracking the  Target with the Pipper. In addition Target acceleration and shooter parameters  (Airspeed, Range, G and POM( remain constant during the Time of Flight (TOF(.
   SOLO F16 3.  The Snap Shot Display is a historic tracer Gunsight. The principle of the System is     to let the Pilot see where the projectiles would be once they have left the Gun.     The Snap Shot Algorithm functions completely independent of Target Parameters      except range, which is used the Pipper on the Continuously Computed Impact Line     (CCIL(.  The key is that the System is Historic and not Predictive in nature.     It is very hard to use it as an aiming reference and is not recommended because of     the TOF lag in the presentation and the difficulty in managing the sight. However,      it does provide an excellent shot evaluation capability. The accuracy of the sight is      within 4 – 5 mils at 2000’ range as long as the Pilot have not been doing any rapid     rolling maneuvers. LCOS and Snap Shot always be called up together when    employing the Gun, use LCOS to aim with and Snap Shot to evaluate the shot. 4.  The EEGS is a combination LCOS and Director Gunsight available in F16C.     It provides the capability to accurately employ the Gun at all aspects, with or without     a Radar Lock, against an evasive or predictable Target, and out to maximum Gun      Effective Range.      The EEGS consists of Five Levels of Displays, each providing an increasing level     of capability depending upon Radar knowledge of Target Parameters (Range,     Velocity and Acceleration(. As the Radar Locks on to the Target, the Sight Symbology    smoothly transitions from Level II to Level V, without any large transient motions    typical of LCOS mechanization.
   SOLO F16 F16 HUD, Movie F-16 Cockpit, avionics and radar, Movie GR F-16 Vs TURK F-16real video with sound, Movie EEGS Level 1 The lowest level of symbology, Level I, consists of the Gun Cross and is used in the  Event Hud or System Failure. The Symbol is the same as the current LCOSS Gun Cross.
   SOLO F16 Level II is the basic No-Lock Symbology. It consists of the funnel and the Multiple Reference Gunsight (MRGS( lines. In Level II and III, the dynamics of the funnel are based on a traditional LCOS system. Ranging can be obtained from wingspan   matching. The funnel is used in low aspect (up to 50 ͦ ( or high aspect (130 ͦ to  180 ͦ( shots to establish the Aircraft in the proper POM and to track the Target.  The top of the funnel is 600’ range and the bottom in the between 2500’ and 3000’,  depending upon altitude.   An accurate aiming solution exists when  (1(The Target is being tracked at the point in the funnel where the wingspan is         equal to the funnel width (assuming the proper wingspan is set in the DED( (2( The shooter rate of turn approaches that  of the LOS to the Target. The only assumption here is that the Target is turning into the attack. The Pilot is thereby provided a Sight with a good estimation of proper Lead Angle  out to approximately 1500’, where the width and slope of the funnel decreases to  the point where wingspan matching is no longer accurate. The MRGS lines are  used in high LOS rate attacks (such as Beam Aspect against a High Speed Target( To put the Airc raft in the Target POM with excess Lead. Finally, Level II  Symbology includes the Launch Envelopes Display System (LEDS(, simulated  rounds which are fired at a rate of five per second while the trigger is depressed  and  are displayed on the HUD as dot pairs. The dot pairs move downward across the  HUD in the same way that tracers would move had they been fired, and their width EEGS Level II
   SOLO F16
   SOLO F16
   SOLO F16
   SOLO F16
   SOLO F16
   SOLO F16
   SOLO F16
   SOLO F16
   SOLO F16
64 References Anthony L. Leatham, “A Digital Lead Computing Optical Sight Model”, AD-786464,  Air Force Academy, 1974 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996 http://en.wikipedia.org/wiki AD-A208651, “Evaluation of Head-Up Displays Format for the F/A-18 Hornet”,  Leah M. Roust, March 1989 Thesis, Naval Postgraduate School, Montery, CA,  USA
65 SOLO Technion Israeli Institute of Technology 1964 – 1968 BSc EE 1968 – 1971 MSc EE Israeli Air Force 1970 – 1974 RAFAEL Israeli Armament Development Authority 1974 – 2013 Stanford University 1983 – 1986 PhD AA
66 Performance of Aircraft Cannons in terms of their Employment in Air Combat
67 Performance of Aircraft Cannons in terms of their Employment in Air Combat
68 Performance of Aircraft Cannons in terms of their Employment in Air Combat
69 Performance of Aircraft Cannons in terms of their Employment in Air Combat
70
71
72
73

More Related Content

PPT
7 air-to-air combat
bySolo Hermelin
 
PPTX
Lockheed Martin F35 Lightning II(Aerodynamics Presentation)
bySYEDMOEEDHUSSAIN1
 
PPT
8 fighter aircraft avionics-part i
bySolo Hermelin
 
PPT
11 fighter aircraft avionics - part iv
bySolo Hermelin
 
PDF
BVR combat brief
byPicard578
 
PPT
3 modern aircraft cutaway
bySolo Hermelin
 
PPT
10 fighter aircraft avionics - part iii
bySolo Hermelin
 
PPT
Aerodynamics part i
bySolo Hermelin
 
7 air-to-air combat
bySolo Hermelin
 
Lockheed Martin F35 Lightning II(Aerodynamics Presentation)
bySYEDMOEEDHUSSAIN1
 
8 fighter aircraft avionics-part i
bySolo Hermelin
 
11 fighter aircraft avionics - part iv
bySolo Hermelin
 
BVR combat brief
byPicard578
 
3 modern aircraft cutaway
bySolo Hermelin
 
10 fighter aircraft avionics - part iii
bySolo Hermelin
 
Aerodynamics part i
bySolo Hermelin
 

What's hot

PDF
F 35 brief
byPicard578
 
PDF
F 35 Production
byandycosterton
 
PPTX
F-35, Stealth and Designing a 21st Century Fighter from the Ground Up
byICSA, LLC
 
PPTX
Combat Systems Fusion Engine for the F-35
byICSA, LLC
 
PDF
Air Dominance
byPhil "Filvis" Rechnitzer; MBA, MA
 
PPT
F 15 vs su-27
bymishanbgd
 
PDF
Naval Aircraft & Missiles Web
byLynn Seckinger
 
PPTX
Stealth technology in aircrafts
bySurender Singh
 
PPT
Anti ballistic missiles i
bySolo Hermelin
 
PPTX
F 35 and Current Weapons
byICSA, LLC
 
PDF
Air Force Association - F-22 Versus F-35 Comparison
byTommy Toy
 
PPTX
1 typhoon, rafale, gripen
byPaul Hodges
 
PPT
F-35 Multi-Role
byStephen Trimble
 
PPT
Anti ballistic missiles ii
bySolo Hermelin
 
PPTX
Design of fighter aircraft presentation
byDudekula Jamal
 
PDF
F 35 brochure
byamenendezam
 
PPTX
Lockheed Martin F35 Lightning II(Propulsion Presentation)
bySYEDMOEEDHUSSAIN1
 
PPTX
AIM-120, USA - Advanced Medium Range Air-to-Air Missile
byhindujudaic
 
PPT
guided missile
byArbaz Khan
 
PPTX
Guided missiles
byAvinash Kharche
 
F 35 brief
byPicard578
 
F 35 Production
byandycosterton
 
F-35, Stealth and Designing a 21st Century Fighter from the Ground Up
byICSA, LLC
 
Combat Systems Fusion Engine for the F-35
byICSA, LLC
 
Air Dominance
byPhil "Filvis" Rechnitzer; MBA, MA
 
F 15 vs su-27
bymishanbgd
 
Naval Aircraft & Missiles Web
byLynn Seckinger
 
Stealth technology in aircrafts
bySurender Singh
 
Anti ballistic missiles i
bySolo Hermelin
 
F 35 and Current Weapons
byICSA, LLC
 
Air Force Association - F-22 Versus F-35 Comparison
byTommy Toy
 
1 typhoon, rafale, gripen
byPaul Hodges
 
F-35 Multi-Role
byStephen Trimble
 
Anti ballistic missiles ii
bySolo Hermelin
 
Design of fighter aircraft presentation
byDudekula Jamal
 
F 35 brochure
byamenendezam
 
Lockheed Martin F35 Lightning II(Propulsion Presentation)
bySYEDMOEEDHUSSAIN1
 
AIM-120, USA - Advanced Medium Range Air-to-Air Missile
byhindujudaic
 
guided missile
byArbaz Khan
 
Guided missiles
byAvinash Kharche
 

Similar to 6 computing gunsight, hud and hms

PDF
Stevenson f 22 brief
byPicard578
 
PPTX
PPT ON GUIDED MISSILES
bySneha Jha
 
PPT
Guided Missiles2 2003
byRakesh Nair A
 
PPT
Innovation In Military Technology
byChristopher Chong
 
PPTX
Secret History of Silicon Valley - Master Slide Deck
byStanford University
 
PDF
Steve Blank's Secret History of Silicon Valley Computer History Museum 120708...
byStanford University
 
PPTX
505 Army Base Workshop
byAvnish Gaur
 
PPTX
pawan ppt
byPawan Pandey
 
PDF
Technical data PULSAR Digisight LRF Riflescopes | Optics Trade
byOptics-Trade
 
PPTX
How Military sector change the GIS world
byPRASANNA KUMAR
 
PDF
Design and implementation of a directional
byAlexander Decker
 
PPTX
Small Arms Lethality variables 1.6e DRAFT
byJA Larson
 
PDF
Make Tea Not War
bySecurity B-Sides
 
PDF
Bmds briefing12
byLsquirrel
 
PDF
3 Dec 2013 CDE enduring challenge competition briefings
byDefence and Security Accelerator
 
Stevenson f 22 brief
byPicard578
 
PPT ON GUIDED MISSILES
bySneha Jha
 
Guided Missiles2 2003
byRakesh Nair A
 
Innovation In Military Technology
byChristopher Chong
 
Secret History of Silicon Valley - Master Slide Deck
byStanford University
 
Steve Blank's Secret History of Silicon Valley Computer History Museum 120708...
byStanford University
 
505 Army Base Workshop
byAvnish Gaur
 
pawan ppt
byPawan Pandey
 
Technical data PULSAR Digisight LRF Riflescopes | Optics Trade
byOptics-Trade
 
How Military sector change the GIS world
byPRASANNA KUMAR
 
Design and implementation of a directional
byAlexander Decker
 
Small Arms Lethality variables 1.6e DRAFT
byJA Larson
 
Make Tea Not War
bySecurity B-Sides
 
Bmds briefing12
byLsquirrel
 
3 Dec 2013 CDE enduring challenge competition briefings
byDefence and Security Accelerator
 

More from Solo Hermelin

PPT
9 fighter aircraft avionics-part ii
bySolo Hermelin
 
PPT
13 fixed wing fighter aircraft- flight performance - i
bySolo Hermelin
 
PPT
2 aircraft flight instruments
bySolo Hermelin
 
PPT
14 fixed wing fighter aircraft- flight performance - ii
bySolo Hermelin
 
PPT
15 sky cars
bySolo Hermelin
 
PPT
2Anti-aircraft Warhead
bySolo Hermelin
 
PPT
1 susceptibility vulnerability
bySolo Hermelin
 
PPT
Analytic dynamics
bySolo Hermelin
 
PPT
Keplerian trajectories
bySolo Hermelin
 
PPT
Inner outer and spectral factorizations
bySolo Hermelin
 
PPT
3 earth atmosphere
bySolo Hermelin
 
PPT
Calculus of variation problems
bySolo Hermelin
 
PPT
12 performance of an aircraft with parabolic polar
bySolo Hermelin
 
PPT
Stabilization of linear time invariant systems, Factorization Approach
bySolo Hermelin
 
PPT
4 navigation systems
bySolo Hermelin
 
PPT
5 introduction to quantum mechanics
bySolo Hermelin
 
PPT
Reduced order observers
bySolo Hermelin
 
PPT
Slide Mode Control (S.M.C.)
bySolo Hermelin
 
PPT
Calculus of variations
bySolo Hermelin
 
PPT
Sliding Mode Observers
bySolo Hermelin
 
9 fighter aircraft avionics-part ii
bySolo Hermelin
 
13 fixed wing fighter aircraft- flight performance - i
bySolo Hermelin
 
2 aircraft flight instruments
bySolo Hermelin
 
14 fixed wing fighter aircraft- flight performance - ii
bySolo Hermelin
 
15 sky cars
bySolo Hermelin
 
2Anti-aircraft Warhead
bySolo Hermelin
 
1 susceptibility vulnerability
bySolo Hermelin
 
Analytic dynamics
bySolo Hermelin
 
Keplerian trajectories
bySolo Hermelin
 
Inner outer and spectral factorizations
bySolo Hermelin
 
3 earth atmosphere
bySolo Hermelin
 
Calculus of variation problems
bySolo Hermelin
 
12 performance of an aircraft with parabolic polar
bySolo Hermelin
 
Stabilization of linear time invariant systems, Factorization Approach
bySolo Hermelin
 
4 navigation systems
bySolo Hermelin
 
5 introduction to quantum mechanics
bySolo Hermelin
 
Reduced order observers
bySolo Hermelin
 
Slide Mode Control (S.M.C.)
bySolo Hermelin
 
Calculus of variations
bySolo Hermelin
 
Sliding Mode Observers
bySolo Hermelin
 

Recently uploaded

PDF
Child Development 9th Edition PDF Textbook
bywosarix923
 
PPTX
Lateral Thinking in - Managerial Skills
bycscprabh
 
PDF
Campbell Biology 12th Edition PDF Textbook
bywosarix923
 
PDF
Biopsychology 10th Edition PDF by John P. J. Pinel
bykonivon907
 
PPT
LIPIDS, LIPOPROTEINS AND DISORDERS-2.ppt
byikofrank15
 
PDF
Cellular Communication: Signal Transduction Pathway
byNistarini College, Purulia (W.B) India
 
PDF
Introduction of bioinformatics in hindi ( जैव सूचना विज्ञान का परिचय ) @irfan...
byWorld of Wisdom
 
PPTX
Biodiversity-Chapter-5-Topic-1-Diversity-Indices.pptx
byannep5208
 
PDF
glyoproteins and its types n o gpi linked pdf.pdf
byrutikbait012
 
PDF
Cognitive Architectures: Information Compression, Meaning-Making, and Drift i...
byCognitive Drift Institute
 
PPTX
Inter-process Communication in operating systems
bycscprabh
 
PPTX
Determination of Permanent Wilting Point (PWP) by Sunflower pot culture techn...
bySaurabh Upadhyay
 
PPTX
What is Blockchain Security is managed in order to protect some vital informa...
bycscprabh
 
PPTX
Epigenetics (Protein translation, Genetic Code, Steps involved in Translation...
byRashmiMG2
 
PPTX
CLASSIFICATION OF LIVING ORGANISMS: THE THREE DOMAINS OF LIFE
byHOME
 
PDF
Cosmic-Ray Bath in a Past Supernova Gives Birth to Earth-Like Planets
bySérgio Sacani
 
PDF
Ch3-phys701-Maram optics for 1234566.pdf
byssuserd90459
 
PDF
Cloud microphysical processes: graduate lecture slides on Cloud Physics UNR C...
byDDM
 
PDF
MultispacecraftMeasurementsof theEvolvingGeometryof theSolarAlfvénSurface ove...
bySérgio Sacani
 
PDF
Gaussian Multiplicative Chaos: Theory, Structure, and Applications
byBob Marcus
 
Child Development 9th Edition PDF Textbook
bywosarix923
 
Lateral Thinking in - Managerial Skills
bycscprabh
 
Campbell Biology 12th Edition PDF Textbook
bywosarix923
 
Biopsychology 10th Edition PDF by John P. J. Pinel
bykonivon907
 
LIPIDS, LIPOPROTEINS AND DISORDERS-2.ppt
byikofrank15
 
Cellular Communication: Signal Transduction Pathway
byNistarini College, Purulia (W.B) India
 
Introduction of bioinformatics in hindi ( जैव सूचना विज्ञान का परिचय ) @irfan...
byWorld of Wisdom
 
Biodiversity-Chapter-5-Topic-1-Diversity-Indices.pptx
byannep5208
 
glyoproteins and its types n o gpi linked pdf.pdf
byrutikbait012
 
Cognitive Architectures: Information Compression, Meaning-Making, and Drift i...
byCognitive Drift Institute
 
Inter-process Communication in operating systems
bycscprabh
 
Determination of Permanent Wilting Point (PWP) by Sunflower pot culture techn...
bySaurabh Upadhyay
 
What is Blockchain Security is managed in order to protect some vital informa...
bycscprabh
 
Epigenetics (Protein translation, Genetic Code, Steps involved in Translation...
byRashmiMG2
 
CLASSIFICATION OF LIVING ORGANISMS: THE THREE DOMAINS OF LIFE
byHOME
 
Cosmic-Ray Bath in a Past Supernova Gives Birth to Earth-Like Planets
bySérgio Sacani
 
Ch3-phys701-Maram optics for 1234566.pdf
byssuserd90459
 
Cloud microphysical processes: graduate lecture slides on Cloud Physics UNR C...
byDDM
 
MultispacecraftMeasurementsof theEvolvingGeometryof theSolarAlfvénSurface ove...
bySérgio Sacani
 
Gaussian Multiplicative Chaos: Theory, Structure, and Applications
byBob Marcus
 

6 computing gunsight, hud and hms

Editor's Notes

  • #5 http://en.wikipedia.org/wiki/Gyro_gunsight
  • #6 http://en.wikipedia.org/wiki/Gyro_gunsight
  • #7 http://spitfiresite.com/2007/11/mark-ii-gyro-gunsight.html http://www.youtube.com/watch?v=0SBE1hRVdQY
  • #8 http://en.wikipedia.org/wiki/Gyro_gunsight http://www.youtube.com/watch?v=36eLp9XGNjs
  • #9 http://articles.janes.com/articles/Janes-Avionics/AN-ASG-26A-Lead-computing-optical-sight-United-States.html
  • #36 http://en.wikipedia.org/wiki/Head-up_display
  • #37 http://en.wikipedia.org/wiki/Head-up_display
  • #38 http://www.ausairpower.net/TE-Fighter-Cockpits.html
  • #39 http://en.wikipedia.org/wiki/Head-up_display
  • #40 http://en.wikipedia.org/wiki/Head-up_display
  • #41 AD-A208651, “Evaluation of Head-Up Displays Format for the F/A-18 Hornet”, Leah M. Roust, March 1989 Thesis, Naval Postgraduate School, Montery, CA, USA
  • #44 http://en.wikipedia.org/wiki/Head-up_display
  • #45 F-15E_info Strike Eagle reference and resources - F-15E_info - Head-Up Display.mht
  • #46 http://en.wikipedia.org/wiki/Head-up_display
  • #52 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #53 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #54 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996 http://www.youtube.com/watch?v=BHx-OWdHqf8 http://www.youtube.com/watch?v=Aq5HXTGUHGI http://www.youtube.com/watch?v=gv1S1w2upkM
  • #55 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #56 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #57 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #58 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #59 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #60 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #61 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #62 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #63 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #64 “Multi-Command Handbook 11-F16” Volume 5, Effective Date: 10 May 1996
  • #67 M. Janošek, A. Svoboda, “Performance of Aircraft Cannons in terms of their Employment in Air Combat” , Advanced in MT, 2007 http://aimt.unob.cz/articles/07_02/07_02%20(3).pdf
  • #68 M. Janošek, A. Svoboda, “Performance of Aircraft Cannons in terms of their Employment in Air Combat” , Advanced in MT, 2007 http://aimt.unob.cz/articles/07_02/07_02%20(3).pdf
  • #69 M. Janošek, A. Svoboda, “Performance of Aircraft Cannons in terms of their Employment in Air Combat” , Advanced in MT, 2007 http://aimt.unob.cz/articles/07_02/07_02%20(3).pdf
  • #70 M. Janošek, A. Svoboda, “Performance of Aircraft Cannons in terms of their Employment in Air Combat” , Advanced in MT, 2007 http://aimt.unob.cz/articles/07_02/07_02%20(3).pdf
  • #71 http://greekmilitary.net/GreekF16.htm
  • #72 http://greekmilitary.net/GreekF16.htm
  • #73 Shaw, “Fighter Combats, Tactics and Maneuvering”, Naval Institute Press, 1985 , Internet
  • #74 Shaw, “Fighter Combats, Tactics and Maneuvering”, Naval Institute Press, 1985 , Internet