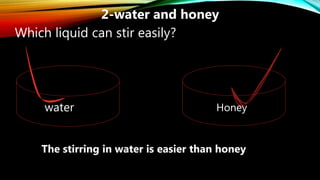
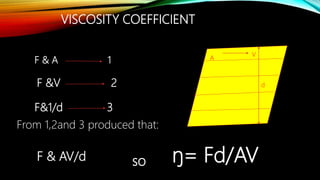
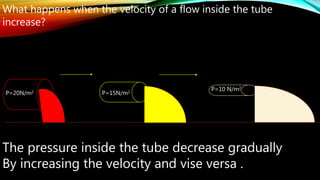
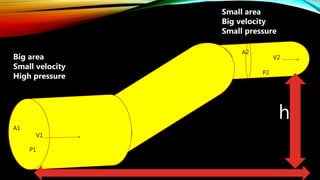
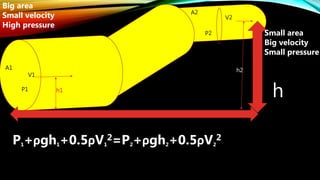
This document discusses key concepts in fluid dynamics, including: 1. Fluid flow, viscosity, and Bernoulli's equation are the main properties of fluid dynamics. Fluid flow is the movement of a fluid and can be steady or turbulent. Viscosity is the resistance of fluid layers sliding past one another. 2. Bernoulli's equation relates pressure, velocity, and elevation in fluid systems. It states that the total mechanical energy (pressure + potential + kinetic energy) remains constant in fluid flow. Higher velocities correspond to lower pressures. 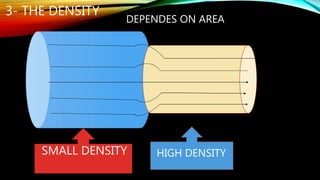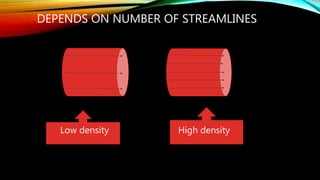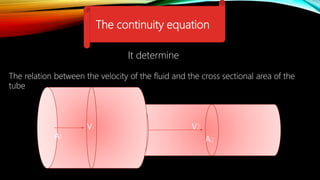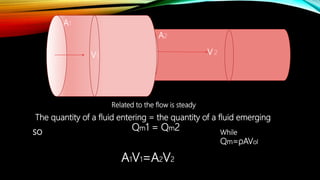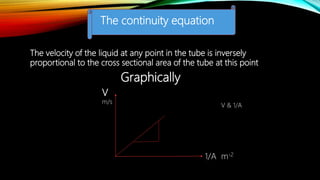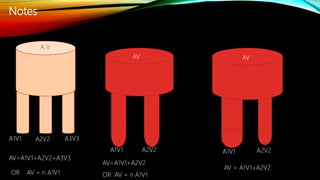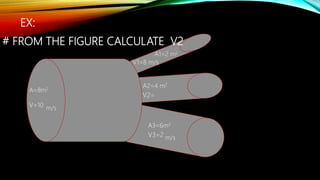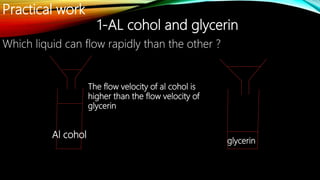3. Other topics covered include streamlines, continuity equation, rate of flow, factors affecting viscosity, and examples applying Bernoulli's equation. The goal is to analyze pressure and velocity in various

1. FLUID DYNAMICS

2. GOAL
Apply principle of fluid dynamics to determine pressure and
velocity in a variety of typical fluid systems

3. THE PROPERTIES OF FLUID DYNAMICS
1-The flow
2-Viscosity
3- Bernoulli's equation

4. At first the flow
What is the flow?
It is the movement of a fluid in a certain direction

5. Notes
1-THE layers

6. 2- LINES
( STREAMELNE)
UN REAL lines

7. 3- THE DENSITY
DEPENDES ON AREA
SMALL DENSITY HIGH DENSITY

8. High densityLow density
DEPENDS ON NUMBER OF STREAMLINES

9. THE DENSITY OF
STREAMLINES
IT IS THE NUMBER OF STREAMLINES THAT PASSING
PERPENDICULAR TO A UNIT AREA AT A CERTAIN
POINT.

10. STREAMLINES
It is un real lines that determine the path for each part of a liquid
during the flow inside the tube by steady flow

11. PROPERTIES OF STREAMLINES
1- un real lines , not intersect each other.
2 - The number of streamlines not change by changing the
area , but the density of streamlines change.
3 – In high velocity the streamlines becomes near
to each other, and
In low velocity the streamlines becomes far to
each other.
4 – The tangent for any point at the streamline
determine the direction of instantaneous
velocity for each small amount of liquid

12. There are two types of flow
Steady ( Laminar ) flow Turbulent flow

13. THE FLOW
1-Is the movement of a fluid
by velocity smaller than the
critical velocity
1-Is the movement of a fluid by
velocity greater than the critical
velocity
Steady flow Turbulent flow
3-Layers of a liquid slide
with respect to each other
smoothly
2-Particles of the liquid
flow IN A continuous path
called streamlines 3-When gas transferred
from small space to a
large space OR When gas
transferred from high
pressure to low pressure
2-It distinguish by
presence of eddy

14. THE CONDITIONS OF A STEADY FLOW
1- THE LIQUID MUST FILLED THE TUBE COMPLETELY.
•
2 – THE APSENCE OF AN EDDIES.
3 – THE APSENCE OF FRICTION FORCE BETWEEN
THE LAYER OF A LIQUID.

15. 4 - THE VELOCITY OF A FLUID NOT INCREASE
THAN THE CRITICAL VELOCITY.
5 - THE QUANTITY OF A FLUID WHICH INTERING FROM ONE
END OF THE TUBE EQUALS THE QUANTITY OF A FLUID
WHICH EMERGING FROM THE OTHER END.

16. THE RATE OF FLOW
• IT IS THE QUANTITY OF A LIQUID WHICH IS FLOW IN A UNIT OF TIME.
There are two types of rate of flow
Mass rate of flow Volume rate of flow

17. Mass rate of the flow Volume rate of the flowFace of comparing
DIFINITION
IT IS THE MASS OF A FLUID
WHICH FLOW IN A UNIT OF
TIME
IT IS THE VOLUME OF THE
FLUID WHICH FLOW IN A UNIT
OF TIME
Qm=m/t
=pvol/t
=PAx/t
=PAV
Qvol=Vol/t
=AX/t
=AV
kg/s m3/s
law
unit

18. The continuity equation
The relation between the velocity of the fluid and the cross sectional area of the
tube
It determine
A1
V1
A2
V2

19. A1
V1
A2
V 2
Related to the flow is steady
The quantity of a fluid entering = the quantity of a fluid emerging
so Qm1 = Qm2 While
Qm=ρAVol
A1V1=A2V2

20. The continuity equation
The velocity of the liquid at any point in the tube is inversely
proportional to the cross sectional area of the tube at this point
Graphically
V
m/s
1/A m-2
V & 1/A

21. Notes
A V
A1V1 A2V2 A3V3
AV=A1V1+A2V2+A3V3
A1V1
AV
A2V2
AV=A1V1+A2V2
OR AV = n A1V1 OR AV = n A1V1
A1V1
AV
A2V2
AV = A1V1+A2V2

22. EX:
# FROM THE FIGURE CALCULATE V2
A=8m2
V=10 m/s
A1=2 m2
V1=8 m/s
A2=4 m2
V2=
A3=6m2
V3=2 m/s

23. The Answer

24. VISCOSITY

25. Practical work
1-AL cohol and glycerin
Al cohol
glycerin
The flow velocity of al cohol is
higher than the flow velocity of
glycerin
Which liquid can flow rapidly than the other ?

26. Honey
2-water and honey
water
Which liquid can stir easily?
The stirring in water is easier than honey

27. 3-water and glycerin
water glycerin
Which ball record a short time ?
The time taken in water is a
smaller than the time taken
in glycerin

28. From the previous experiments
We can found that
Some liquids as ( water and al cohol ) have high flow and
less resistance to allow object to move inside it
This means that they are low viscosity
Some liquids as ( honey and glycerin ) have low flow and
high resistance to allow object to move inside it
This means that they are low viscosity

29. viscosity
It is the property which is responsible for the resistance or friction
between the liquid layers and prevents sliding of layers above each
other

30. Explaining the viscosity
1- friction force
2- force similar to the friction force

31. VISCOSITY COEFFICIENT
V
A
d
F & A 1
F &V 2
F&1/d 3
From 1,2and 3 produced that:
F & AV/d so ŋ= Fd/AV

32. VISCOSITY COEFFICIENT
It is the tangential force acting on a unit area to
perpendicular a unit change in velocity between two layers
at unit distance apart from each other.
ŋ= Fd/AV
THE UNIT IS N.S/m2

33. Factors affecting viscosity
1-Velocity
2- Area
3-Distance
4- viscosity coefficient

34. Bernoulli's Equation

35. 1-Conservation law of energy
It is the relation which explain:
2- the relation between velocity and pressure
OR
Explain the relation between pressure, potential
and kinetic energy

36. Notes FOR APPLYING Bernoulli's EQUATION
1-THE KINETIC ENERGY MUSTNOT CHANGE TO HEAT ENERGY
Or any other form of energy DURING THE FLOW TO KEEP THE
MECHANICAL ENERGY CONESTANT
3- BERNOULLIS CONSTANT CHANGE FROM ONE TUBE TO
OTHER TUBE
2- we apply this equation in the same streameline inside
the tube

37. What happens when the velocity of a flow inside the tube
increase?
The pressure inside the tube decrease gradually
By increasing the velocity and vise versa .
P=20N/m2 P=15N/m2
P=10 N/m2

38. so

39. Bernoulli's determine the relation between the
pressure, kinetic energy and potential energy
function

40. Bernoulli'sprinciple
The sum of pressure ,velocity and stored potential
energy in a unit volume from the fluid equals constant
value

41. A1
V1
P1
h
Big area
Small velocity
High pressure
Small area
Big velocity
Small pressure

42. A1
V1
P1
h
Big area
Small velocity
High pressure
Small area
Big velocity
Small pressure
P1+ρgh1+0.5ρV1
2=P2+ρgh2+0.5ρV2
2
h1
h2

43. In a static liquid
P1-P2=pg(h2-h1)=pgh
But (pgh) is a potential
energy
because if we divide the law
of potential energy by unit
volume the result is pgh
PE/Vol=mgh/Vol=pgh m/Vol =ρ
There for
Related to the liquid is moving so it
should have a Kinetic energy
KE/Vol=1/2mV2/Vol =1/2 ρV2
KE =1/2mV2
If we apply now the law of
conservation energy we can found
that The sum of pressure
,potential energy and kinetic
energy equals constantIn other meaning
Energy at point 1 = energy at
point 2
how
PE=mgh

44. PRESSURE1+POTENTIAL1+KINETIC1=
PRESSURE2+POTENTIAL2+KINETIC2
P1+PE1+KE1=P2+PE2+KE2

45. FORMS OF BERNOULLI.S EQUATION
2
1
P+ρgh+1/2ρv2= P+ρgh+1/2ρv2
P/ρ+gh+1/2v1
2= P/ρ + gh+1/2v2
2
P/ρg+h+1/2v1
2/g= P/ρg +h+1/2v2
2/g
3

46. Ex:
P1=20N/m2
V1=5m/s
P2=
V2=10m/s
Ans:
P1+ρgh1+0.5ρV1
2=P2+ρgh2+0.5ρV2
2
20+0.5X1000X25=P2+0.5X1000X100
12520=P2+10000
P2=