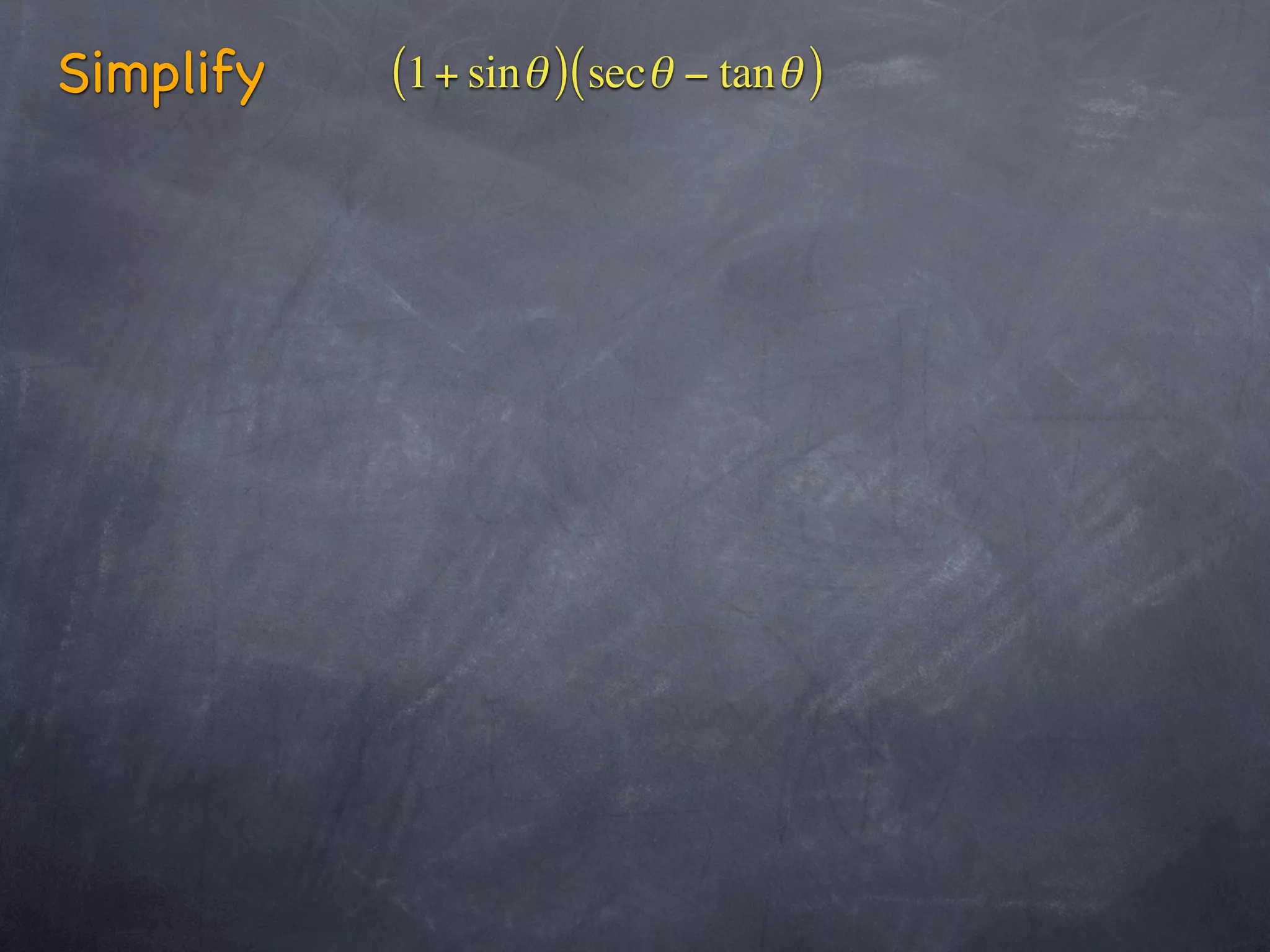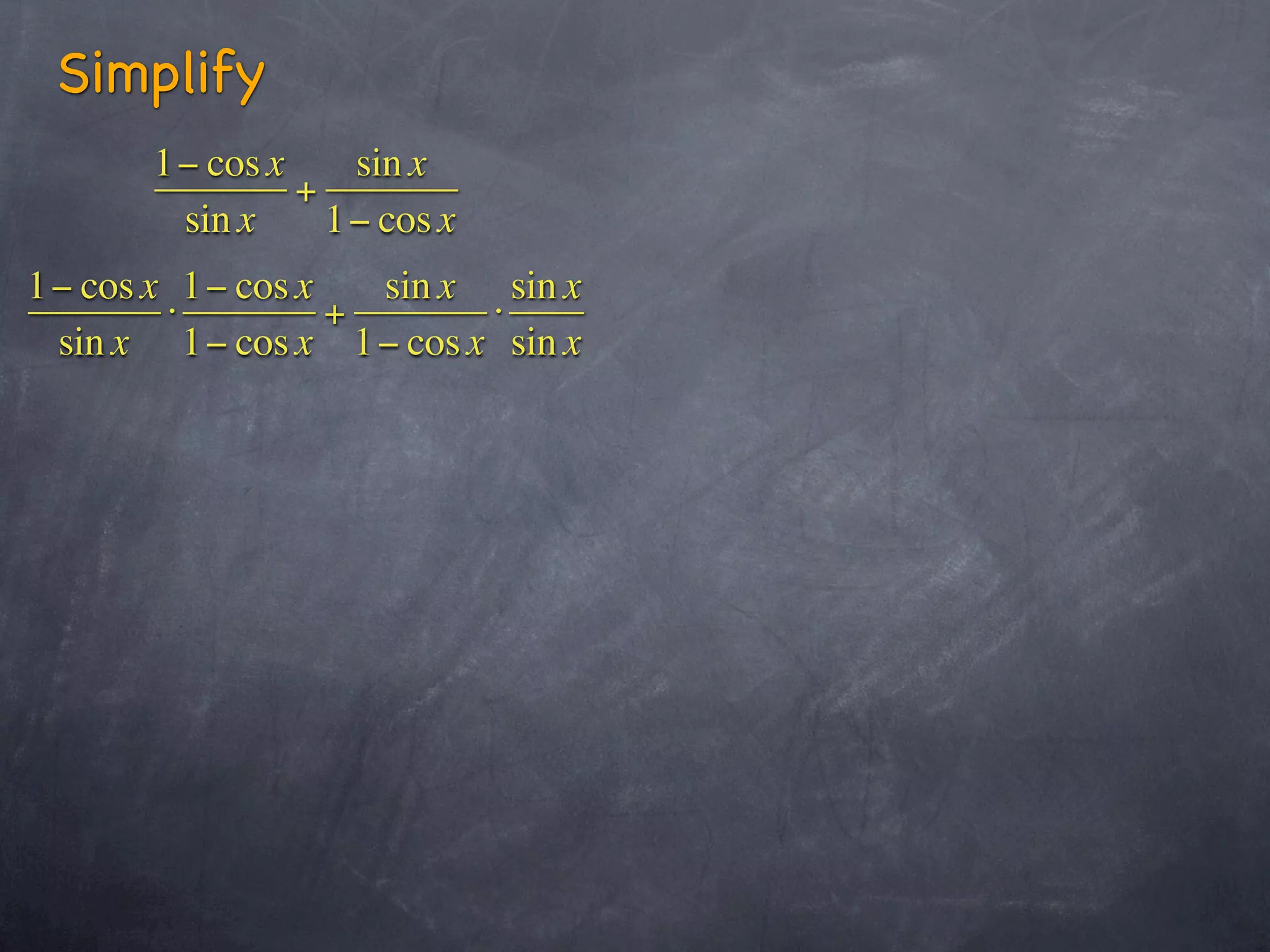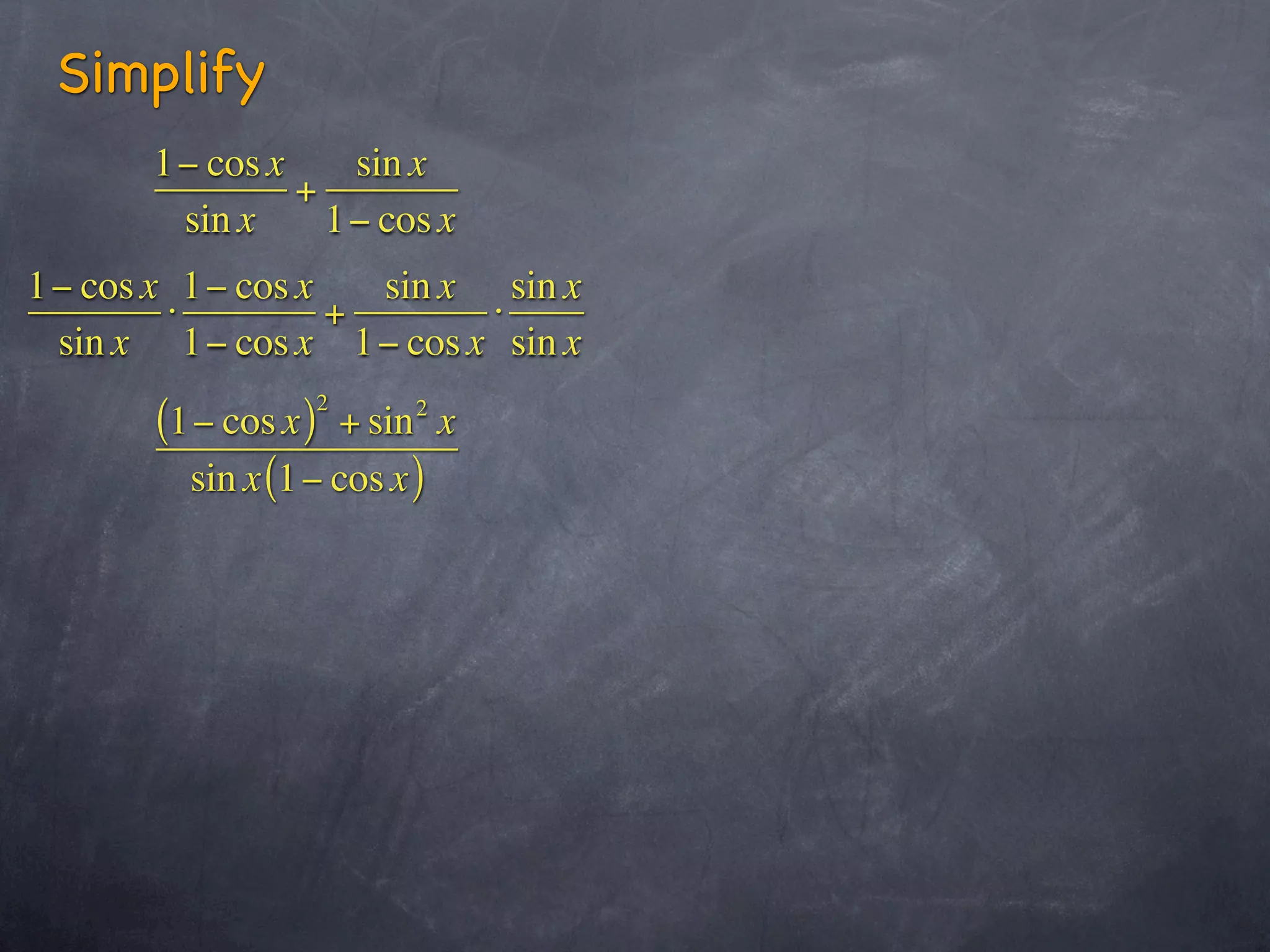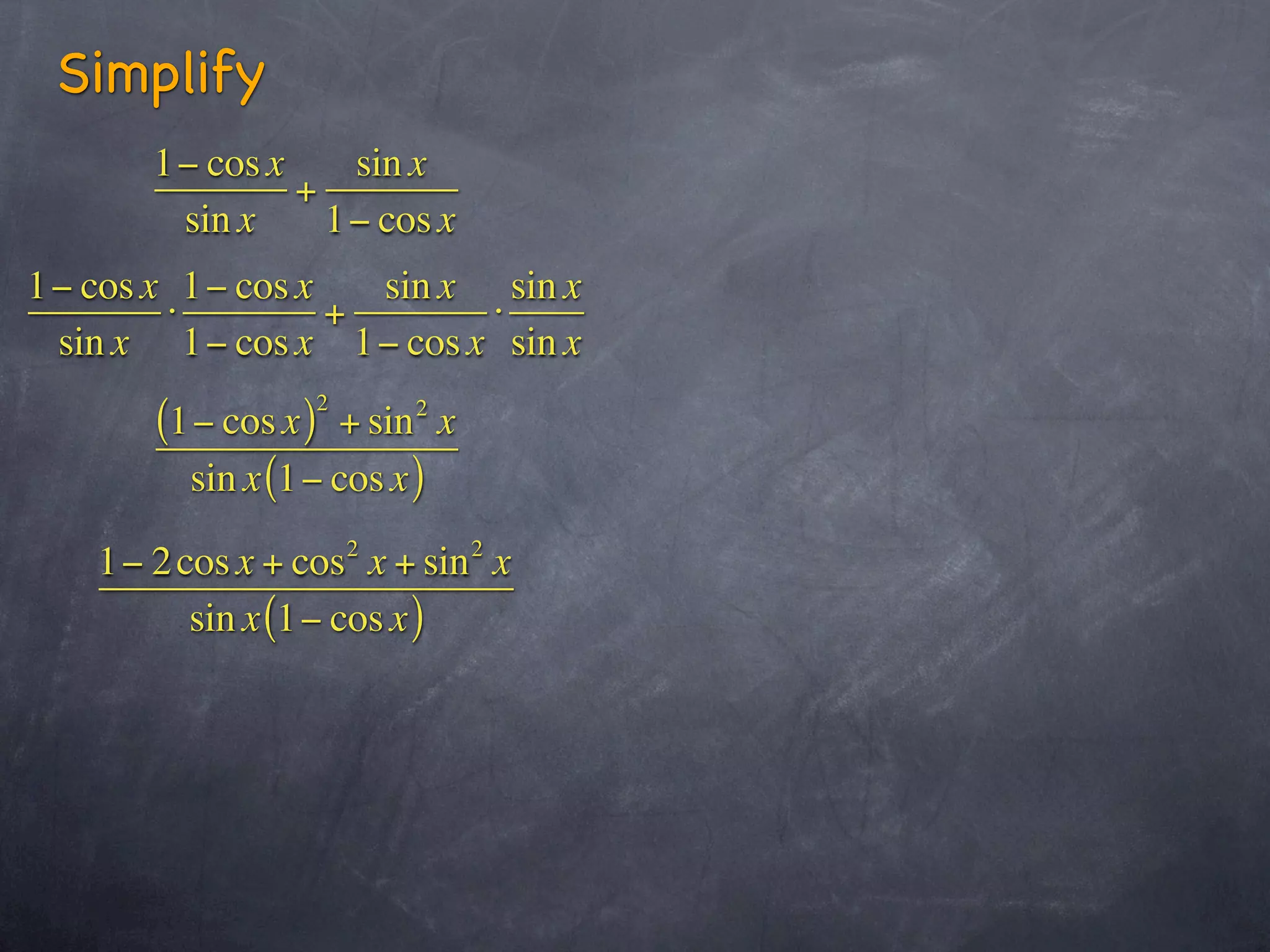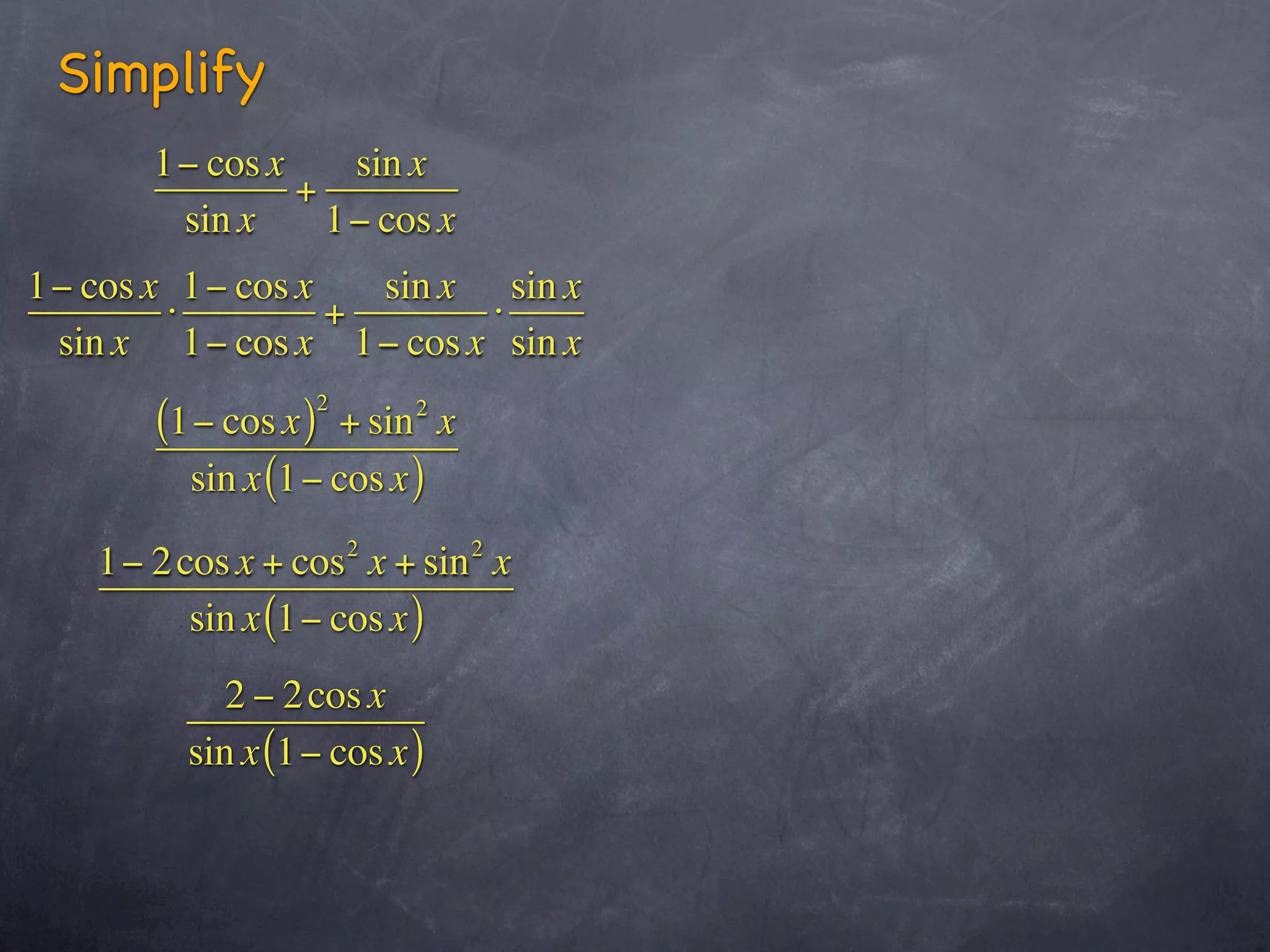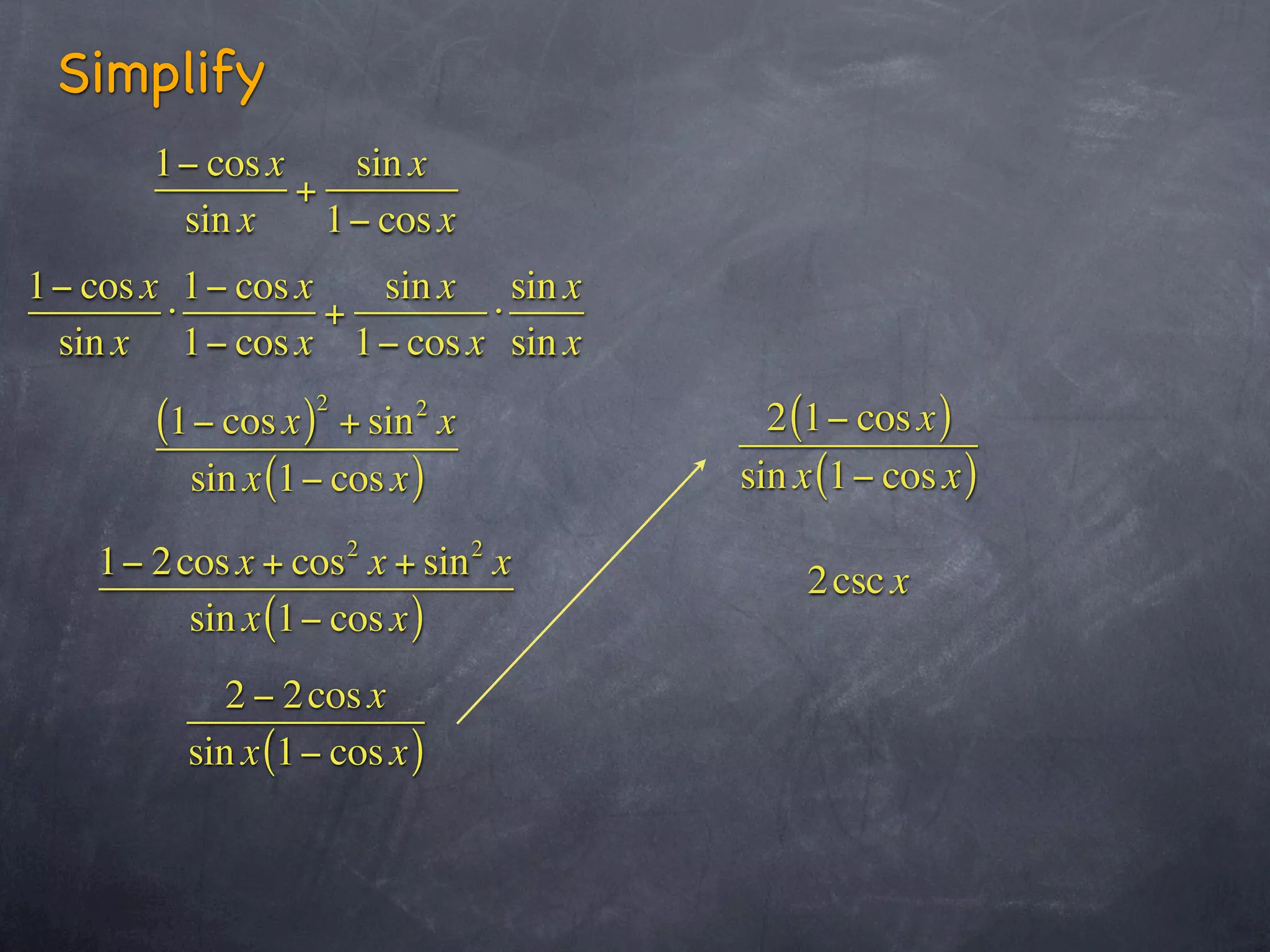This document contains sections from a trigonometry textbook chapter on analytic trigonometry and trigonometric identities. It includes explanations of trigonometric identities and examples of simplifying trigonometric expressions using identities. It also contains a biblical verse and encourages students to study examples, do their homework, and ask questions in class.

1. Chapter 7
Analytic Trigonometry
Matthew 19:25-26
When the disciples heard this, they were greatly
astonished and asked, "Who then can be saved?"
Jesus looked at them and said, "With man this is
impossible, but with God all things are possible."

2. Chapter 7
Analytic Trigonometry
Much of this chapter will be new topics for you.
Read your textbook! Study the examples!!
Keep current with your homework!!!
Matthew 19:25-26
When the disciples heard this, they were greatly
astonished and asked, "Who then can be saved?"
Jesus looked at them and said, "With man this is
impossible, but with God all things are possible."

3. 7.1 Trigonometric Identities

4. 7.1 Trigonometric Identities
An identity is an equation that is true for all values
of the variable in the domain.

5. 7.1 Trigonometric Identities
An identity is an equation that is true for all values
of the variable in the domain.
An equation will be true for one or more, but not
all, values of the variable in the domain.

6. 7.1 Trigonometric Identities
An identity is an equation that is true for all values
of the variable in the domain.
An equation will be true for one or more, but not
all, values of the variable in the domain.
Equation : 4x − 3 = 5

7. 7.1 Trigonometric Identities
An identity is an equation that is true for all values
of the variable in the domain.
An equation will be true for one or more, but not
all, values of the variable in the domain.
Equation : 4x − 3 = 5
2x + 14
Identity : x+7=
2

8. Fundamental Trig Identities
(open books to page 528 ... look at the box)

9. Fundamental Trig Identities
(open books to page 528 ... look at the box)
Reciprocal: you already know these

10. Fundamental Trig Identities
(open books to page 528 ... look at the box)
Reciprocal: you already know these
Pythagorean: hexagon on your Unit Circle

11. Fundamental Trig Identities
(open books to page 528 ... look at the box)
Reciprocal: you already know these
Pythagorean: hexagon on your Unit Circle
Even-Odd: on your help sheet

12. Fundamental Trig Identities
(open books to page 528 ... look at the box)
Reciprocal: you already know these
Pythagorean: hexagon on your Unit Circle
Even-Odd: on your help sheet
Cofunction: on your help sheet

13. Simplifying Trig Expressions

14. Simplifying Trig Expressions
Use identities and other math operations to rewrite
a trig expression

15. Simplifying Trig Expressions
Use identities and other math operations to rewrite
a trig expression
We use this technique a lot when proving trig
identities

16. Simplify (1+ sinθ )(secθ − tanθ )

17. Simplify (1+ sinθ )(secθ − tanθ )
a good tactic is to rewrite everything using sine & cosine

18. Simplify (1+ sinθ )(secθ − tanθ )
a good tactic is to rewrite everything using sine & cosine
⎛ 1 sin θ ⎞
(1+ sinθ ) ⎜ −
⎝ cosθ cosθ ⎟⎠

19. Simplify (1+ sinθ )(secθ − tanθ )
a good tactic is to rewrite everything using sine & cosine
⎛ 1 sin θ ⎞
(1+ sinθ ) ⎜ −
⎝ cosθ cosθ ⎟⎠
⎛ 1− sin θ ⎞
(1+ sinθ ) ⎜
⎝ cosθ ⎠ ⎟

20. Simplify (1+ sinθ )(secθ − tanθ )
a good tactic is to rewrite everything using sine & cosine
⎛ 1 sin θ ⎞
(1+ sinθ ) ⎜ −
⎝ cosθ cosθ ⎟⎠
⎛ 1− sin θ ⎞
(1+ sinθ ) ⎜
⎝ cosθ ⎠ ⎟
2
1− sin θ
cosθ

21. Simplify (1+ sinθ )(secθ − tanθ )
a good tactic is to rewrite everything using sine & cosine
⎛ 1 sin θ ⎞
(1+ sinθ ) ⎜ −
⎝ cosθ cosθ ⎟⎠
⎛ 1− sin θ ⎞
(1+ sinθ ) ⎜
⎝ cosθ ⎠ ⎟
2
1− sin θ
cosθ
2
cos θ
cosθ

22. Simplify (1+ sinθ )(secθ − tanθ )
a good tactic is to rewrite everything using sine & cosine
⎛ 1 sin θ ⎞
(1+ sinθ ) ⎜ −
⎝ cosθ cosθ ⎟⎠
⎛ 1− sin θ ⎞
(1+ sinθ ) ⎜
⎝ cosθ ⎠ ⎟
2
1− sin θ
cosθ
2
cos θ
cosθ
cosθ

23. Simplify
1− cos x sin x
+
sin x 1− cos x

24. Simplify
1− cos x sin x
+
sin x 1− cos x
1− cos x 1− cos x sin x sin x
⋅ + ⋅
sin x 1− cos x 1− cos x sin x

25. Simplify
1− cos x sin x
+
sin x 1− cos x
1− cos x 1− cos x sin x sin x
⋅ + ⋅
sin x 1− cos x 1− cos x sin x
2 2
(1− cos x ) + sin x
sin x (1− cos x )

26. Simplify
1− cos x sin x
+
sin x 1− cos x
1− cos x 1− cos x sin x sin x
⋅ + ⋅
sin x 1− cos x 1− cos x sin x
2 2
(1− cos x ) + sin x
sin x (1− cos x )
1− 2 cos x + cos 2 x + sin 2 x
sin x (1− cos x )

27. Simplify
1− cos x sin x
+
sin x 1− cos x
1− cos x 1− cos x sin x sin x
⋅ + ⋅
sin x 1− cos x 1− cos x sin x
2 2
(1− cos x ) + sin x
sin x (1− cos x )
1− 2 cos x + cos 2 x + sin 2 x
sin x (1− cos x )
2 − 2 cos x
sin x (1− cos x )

28. Simplify
1− cos x sin x
+
sin x 1− cos x
1− cos x 1− cos x sin x sin x
⋅ + ⋅
sin x 1− cos x 1− cos x sin x
2
(1− cos x ) + sin x2
2 (1− cos x )
sin x (1− cos x ) sin x (1− cos x )
1− 2 cos x + cos 2 x + sin 2 x
sin x (1− cos x )
2 − 2 cos x
sin x (1− cos x )

29. Simplify
1− cos x sin x
+
sin x 1− cos x
1− cos x 1− cos x sin x sin x
⋅ + ⋅
sin x 1− cos x 1− cos x sin x
2
(1− cos x ) + sin x2
2 (1− cos x )
sin x (1− cos x ) sin x (1− cos x )
1− 2 cos x + cos 2 x + sin 2 x 2 csc x
sin x (1− cos x )
2 − 2 cos x
sin x (1− cos x )

30. Simplify
csc x cot x
−
sin x tan x

31. Simplify
csc x cot x
−
sin x tan x
1 cos x
sin x − sin x
sin x sin x
1 cos x

32. Simplify
csc x cot x
−
sin x tan x
1 cos x
sin x − sin x
sin x sin x
1 cos x
1 cos 2 x
2
− 2
sin x sin x

33. Simplify
csc x cot x
−
sin x tan x 1− cos 2 x
2
1 cos x sin x
sin x − sin x
sin x sin x
1 cos x
1 cos 2 x
2
− 2
sin x sin x

34. Simplify
csc x cot x
−
sin x tan x 1− cos 2 x
2
1 cos x sin x
sin x − sin x 2
sin x
sin x sin x 2
sin x
1 cos x
1 cos 2 x
2
− 2
sin x sin x

35. Simplify
csc x cot x
−
sin x tan x 1− cos 2 x
2
1 cos x sin x
sin x − sin x 2
sin x
sin x sin x 2
sin x
1 cos x
2 1
1 cos x
2
− 2
sin x sin x

36. For the next few days ... I’ll draw names “out of
the hat”. Those people will be chosen to put a
homework problem on the board. When I draw a
name, it will be for a particular problem ...

37. HW #1
For every pass I caught in a game, I caught a
thousand in practice.
Don Hutson