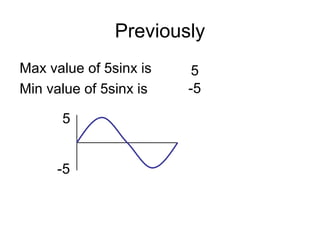
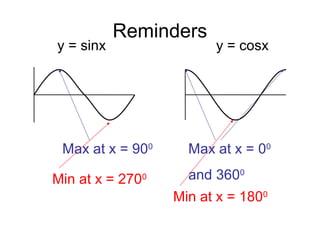
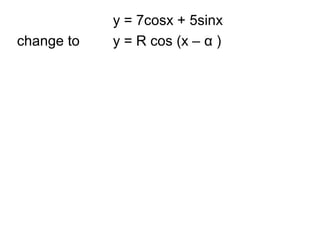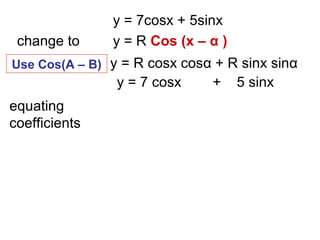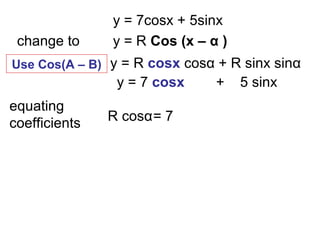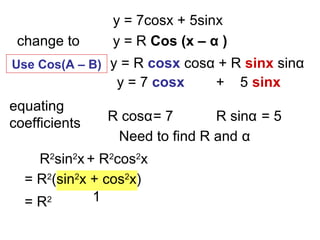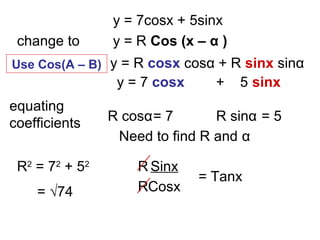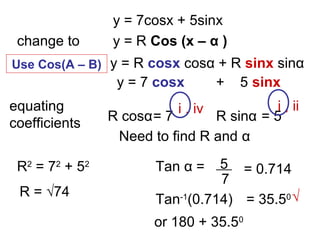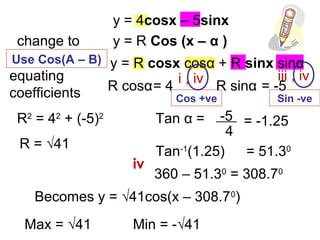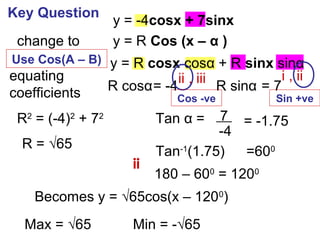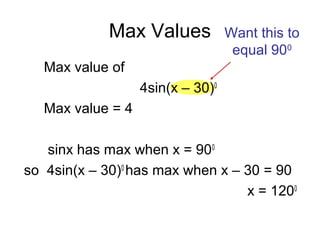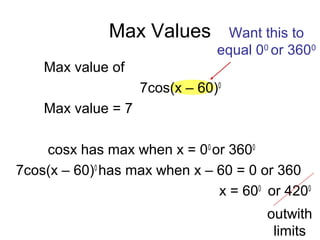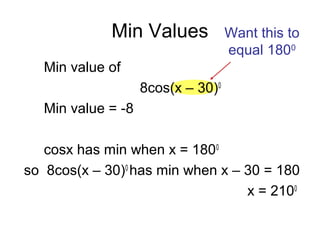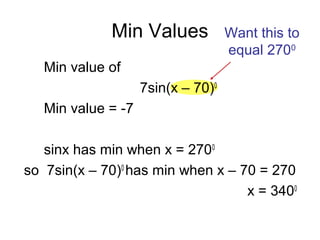The document discusses rewriting trigonometric functions containing both sine and cosine terms in the form Rcos(x-α). It provides examples of rewriting functions such as 7cosx + 5sinx as √74cos(x-35.5). The process involves expanding using the cosine of the difference formula, equating coefficients to find R and α, and checking that R2 equals the sum of the squared coefficients. Max/min values and phase shifts are also discussed. Solving trigonometric equations is demonstrated by rewriting them in the Rcos(x-α) form.

1. Block 2
The Wave Function

2. What is to be learned?
• How the wave function tactic sorts out
functions containing sine and cosine

3. Previously
Max value of 5sinx is
Min value of 5sinx is
5
-5
5
-5

4. How about 7cosx + 5sinx
Need to rewrite with just sine or cosine
y = 7cosx + 5sinx
change to y = R cos (x – α )
Need to find R and α
angle
sin max at x = 900
cos max at x = 00


5. y = 7cosx + 5sinx
change to y = R cos (x – α )

6. y = 7cosx + 5sinx
change to y = R Cos (x – α )
y = 7 cosx + 5 sinx
y = R cosx cosα + R sinx sinα
equating
coefficients
Use Cos(A – B)

7. y = 7cosx + 5sinx
change to y = R Cos (x – α )
y = 7 cosx + 5 sinx
y = R cosx cosα + R sinx sinα
equating
coefficients R cosα= 7
Use Cos(A – B)

8. y = 7cosx + 5sinx
change to y = R Cos (x – α )
y = 7 cosx + 5 sinx
y = R cosx cosα + R sinx sinα
equating
coefficients R cosα= 7 R sinα = 5
Need to find R and α
R2
sin2
x + R2
cos2
x
= R2
Use Cos(A – B)
= R2
(sin2
x + cos2
x)
1

9. y = 7cosx + 5sinx
change to y = R Cos (x – α )
y = 7 cosx + 5 sinx
y = R cosx cosα + R sinx sinα
equating
coefficients R cosα= 7 R sinα = 5
Need to find R and α
R2
= 72
+ 52
Sinx
Cosx
= Tanx
R
R= √74
Use Cos(A – B)

10. y = 7cosx + 5sinx
change to y = R Cos (x – α )
y = 7 cosx + 5 sinx
y = R cosx cosα + R sinx sinα
equating
coefficients R cosα= 7 R sinα = 5
Need to find R and α
R2
= 72
+ 52
Tan α = 5
7
= 0.714
Tan-1
(0.714) = 35.50
or 180 + 35.50
i , iv i , ii
√R = √74
Use Cos(A – B)

11. 7cosx + 5sinx
= √74 cos(x – 35.50
)
Max = √74
Min = -√74
Phase Angle 35.50
Graph moves 35.50
to the right

12. The Wave Function
Rewriting functions containing sine and
cosine in form
R cos( x – α )
Expand using cos (A – B)
Equate Coefficients
R2
= (R cos α)2
+ (R sin α)2
Tan α = R sin α
or similar!
(formula sheet)
R cos α
There can be
only one α

13. y = 4cosx – 5sinx
change to y = R Cos (x – α )
y = R cosx cosα + R sinx sinα
equating
coefficients R cosα= 4 R sinα = -5
R2
= 42
+ (-5)2
Tan α = -5
4
= -1.25
Tan-1
(1.25) = 51.30
360 – 51.30
= 308.70
i , iv iii , iv
iv
R = √41
Min = -√41Max = √41
Becomes y = √41cos(x – 308.70
)
Use Cos(A – B)
Cos +ve Sin -ve

14. y = -4cosx + 7sinx
change to y = R Cos (x – α )
y = R cosx cosα + R sinx sinα
equating
coefficients R cosα= -4 R sinα = 7
R2
= (-4)2
+ 72
Tan α = 7
-4
= -1.75
Tan-1
(1.75) =600
180 – 600
= 1200
ii , iii i , ii
ii
R = √65
Min = -√65Max = √65
Becomes y = √65cos(x – 1200
)
Use Cos(A – B)
Cos -ve Sin +ve
Key Question

15. 5cosx – 7sinx
change to Rsin(x – α ) = Rsinx cosα – Rcosx sinα
- 7sinx + 5cosxEquating
Coefficients

16. 5cosx – 7sinx
change to Rsin(x – α ) = Rsinx cosα – Rcosx sinα
- 7sinx + 5cosxEquating
Coefficients
Rcos α = -7

17. 5cosx – 7sinx
change to Rsin(x – α ) = Rsinx cosα – Rcosx sinα
- 7sinx + 5cosxEquating
Coefficients
Rcos α = -7 Rsin α = 5–
Rsin α = -5

18. Reminders
y = sinx y = cosx
Max at x = 900
Min at x = 2700
Max at x = 00
and 3600
Min at x = 1800

19. Max Values
Max value of
4sin(x – 30)0
Max value = 4
sinx has max when x = 900
so 4sin(x – 30)0
has max when x – 30 = 90
x = 1200
Want this to
equal 900

20. Max Values
Max value of
7cos(x – 60)0
Max value = 7
cosx has max when x = 00
or 3600
7cos(x – 60)0
has max when x – 60 = 0 or 360
x = 600
or 4200
Want this to
equal 00
or 3600
outwith
limits

21. Min Values
Min value of
8cos(x – 30)0
Min value = -8
cosx has min when x = 1800
so 8cos(x – 30)0
has min when x – 30 = 180
x = 2100
Want this to
equal 1800

22. Min Values
Min value of
7sin(x – 70)0
Min value = -7
sinx has min when x = 2700
so 7sin(x – 70)0
has min when x – 70 = 270
x = 3400
Want this to
equal 2700

23. Solve 4cosx + 3sinx = 2
Rcos(x – α) = R cosx cosα + R sinx sinα
Rcosα = 4 Rsinα = 3
R2
= 32
+ 42
Tanα = ¾
R = 5 α = Tan-1
(¾) = 370
Equation becomes 5cos(x – 37) = 2
cos(x – 37) = 0.4
cosA = 0.4 where A = x – 37
cos-1
(0.4) = 660
A = 660
or 2940
x – 37 = 66 or 294
x = 1030
or 3310
Change to form Rcos (x – α)
Ignore for moment
i , iv i , ii


24. Uses of the Wave Function
Gets max and min values.
Helps us sketch the graph
and
Good format to solve Trig Equations
May not tell you to use wave function
- look for mix of sin and cos
If you are not told which expansion to use
– you get to choose!
Rcos(x – α) – very popular!

25. Solve 4cosx – 5sinx = 4
Change to
Gives √41cos(x – 308.70
) = 4
Then √41cos A = 4, where A = x – 308.70
cos A = 4
/√41
etc.
form Rcos(x – α)