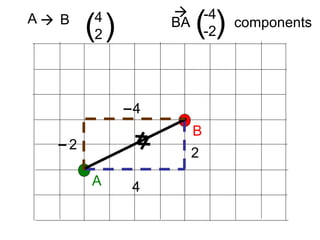
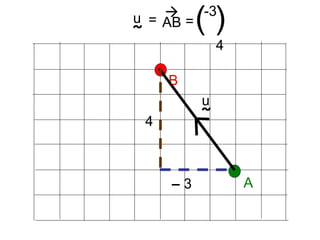
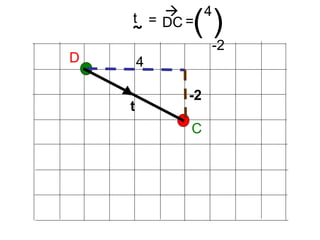
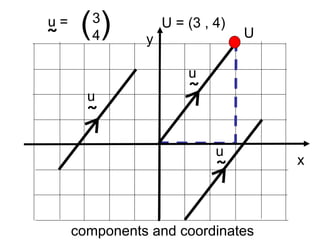
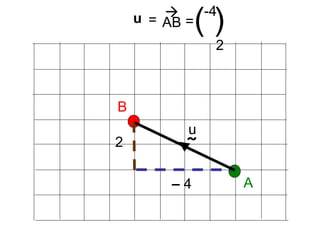
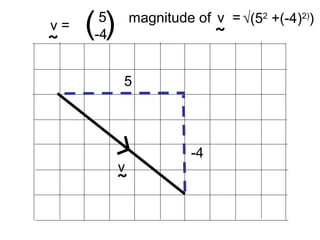
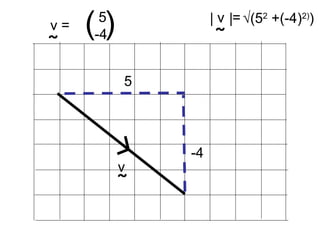
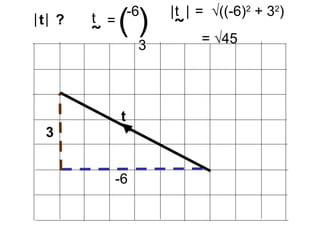
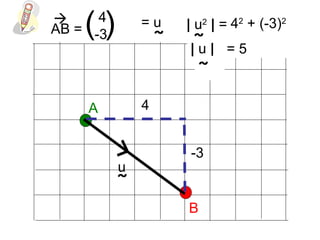
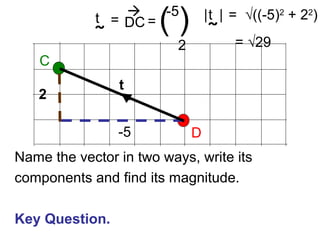
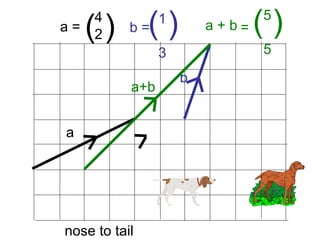
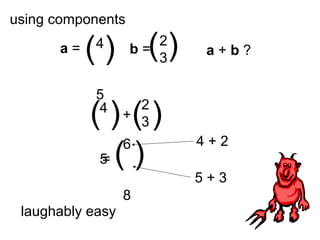
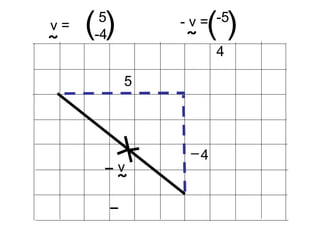
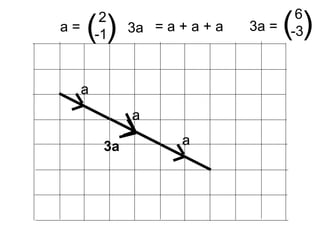
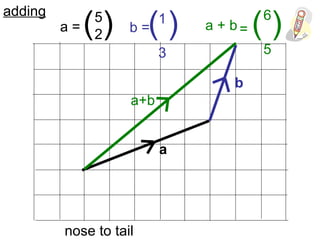
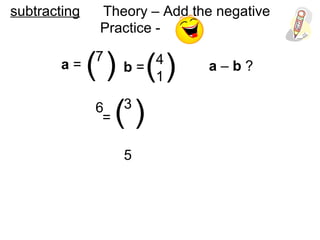
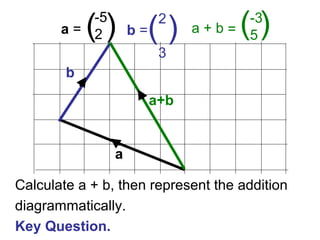
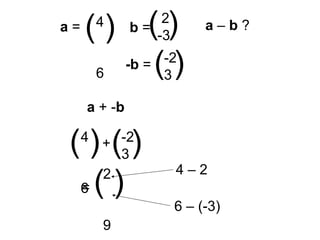Vectors can represent journeys with distance and direction. They have components that work like coordinates and magnitude that is calculated using Pythagoras. Vectors can be added by placing them nose to tail and adding corresponding components, subtracted by adding the negative vector, and multiplied by a scalar by multiplying each component.

1. Block 3
Vectors Introduction

2. What is to be learned?
• What a vector is
• Some other bits and pieces about vectors

3. A vector is
Like a journey
Need
Distance
Direction
- magnitude

4. A
B
A
4
2
4
2( )B BA

4–
2–
-4
-2( ) components

5. A
B
– 3
AB

4
-3
4
( )
u
˜
u
˜
= =

6. C
D
-2
DC

4
4
-2
( )
t
t
˜
= =

7. 3
4( )u =
˜
U = (3 , 4)
x
y U
u
˜
u
˜
u
˜
components and coordinates

8. A
B
– 4
AB

2
-4
2
( )
u
˜
u = =

9. Magnitude of a Vector

10. 5
-4
5
-4( )
v
˜
v =
˜
magnitude of v =
˜
√(52
+(-4)2)
)

11. 5
-4
5
-4( )
v
˜
v =
˜
v =
˜
√(52
+(-4)2)
)| |

12. 3
-6
-6
3
( )
t
t
˜
=
=
t ?| |
t
˜
| | √((-6)2
+ 32
)
= √45

13. Vectors
• Describe a “journey”
– Distance
– Direction
• Numbers work like coordinates
– Called components
• The magnitude of vector is calculated using
pythagoras
 magnitude
a
b
( )u =
˜
| u2
| =
˜
a2
+ b2

14. A
B
4
-3
4
-3( )AB =

u
˜
= u
˜
| u2
| =
˜
42
+ (-3)2
| u |
˜
= 5

15. C
D
2
DC

-5
-5
2
( )
t
t
˜
= = =t
˜
| | √((-5)2
+ 22
)
= √29
Name the vector in two ways, write its
components and find its magnitude.
Key Question.

16. What is to be learned?
• How to add and “subtract” vectors.
• How to multiply a vector by a scalar.

17. Vector Addition

18. a + b
4
2( )a = b =
a+b
nose to tail
1
3
( )
a
b
5
5
= ( )

19. a + b ?( )a = b =( )
= ( )
4
5
2
3
( )4
5
( )2
3+
6
8
4 + 2
5 + 3
using components
laughably easy

20. Vector Subtraction

21. vector subtraction does not exist!
(or does it?)
9 – 7
= 9 + (-7)
we add the negative of the vector

22. 5
–
5
-4( )
v
˜
v =
˜
- v =
˜
–
–
4
-5
4
( )

23. a – b ?( )a = b =( )
= ( )
4
6
2
-3
-b = ( )-2
3
a + -b
( )4
6
( )-2
3
+
2
9
4 – 2
6 – (-3)

24. Multiplying by a scalar

25. 2
-1( )a = 3a
a
= a + a + a
a
a
3a =
6
-3( )
3a

26. Addition, Subtraction and
Multiplication (by a Scalar)
Normal Number

27. a + b
5
2( )a = b =
a+b
nose to tail
1
3
( )
a
b
6
5
= ( )
adding

28. a – b ?( )a = b =( )
= ( )
7
6
4
1
3
5
subtracting Theory – Add the negative
Practice -

29. Scalar Multiplication
( )a =
1
2
3a?
3a = ( )3
6

30. a + b
-5
2( )a = b =
a+b
2
3
( )
a
b
-3
5= ( )
Calculate a + b, then represent the addition
diagrammatically.
Key Question.