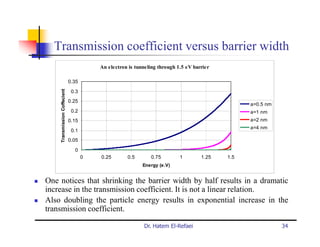
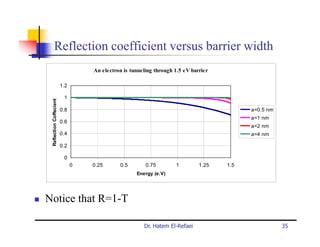
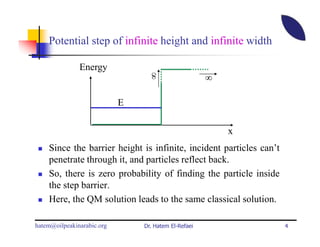
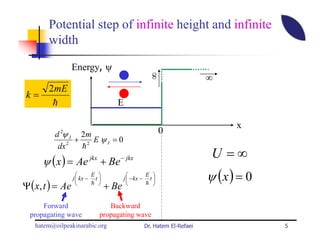
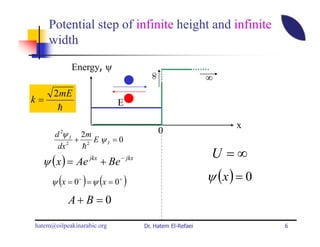
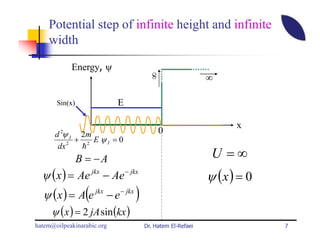
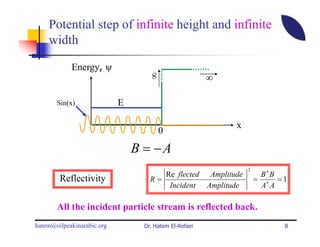
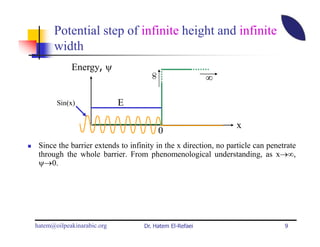
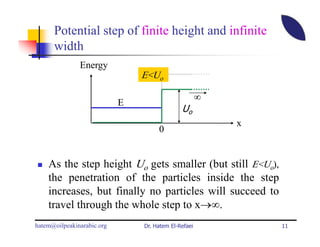
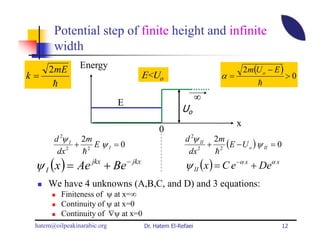
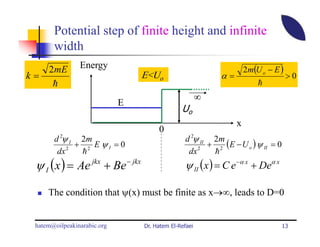
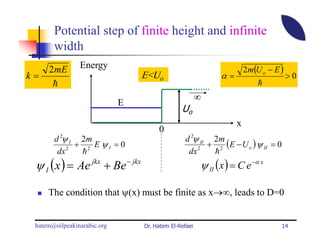
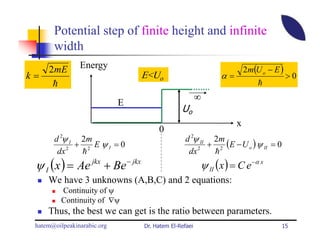
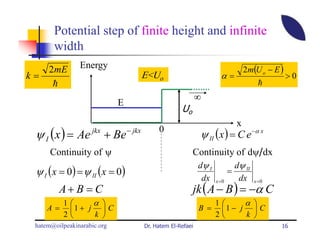
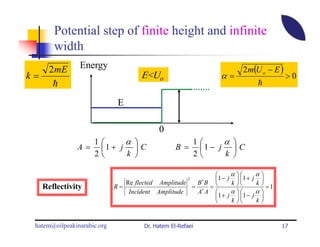
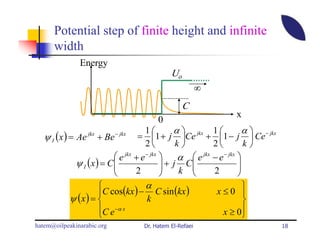
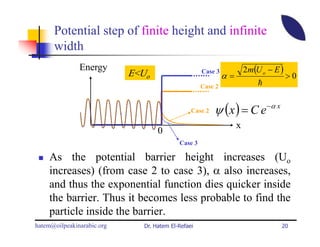
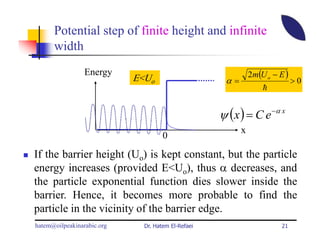
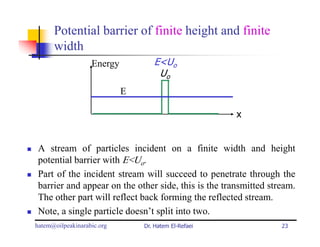
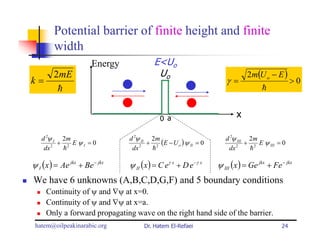
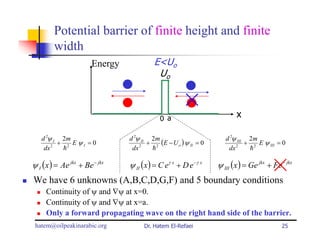
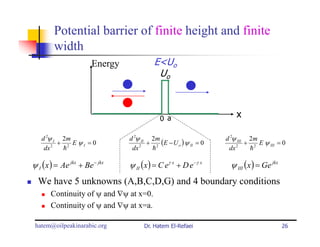
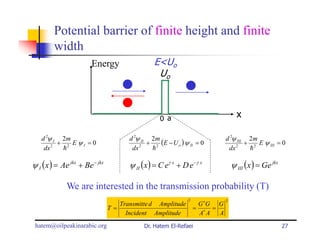
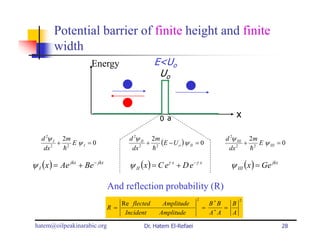
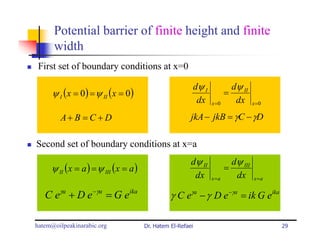
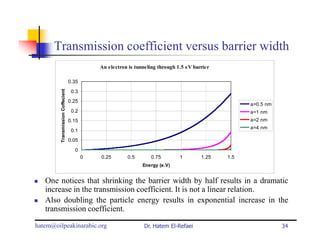
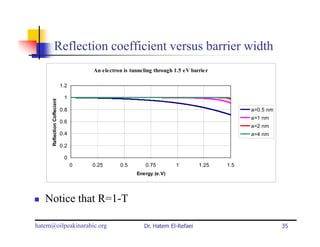
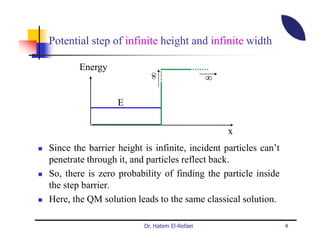
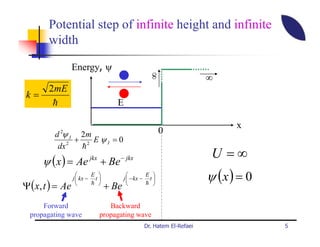
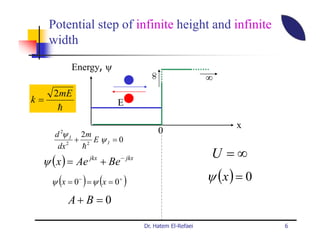
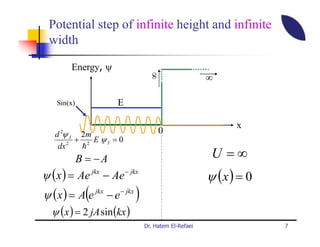
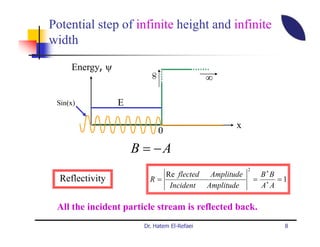
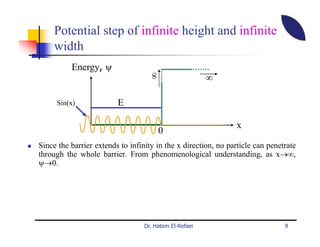
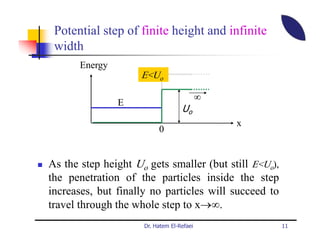
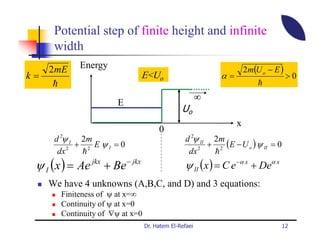
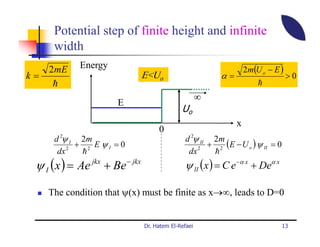
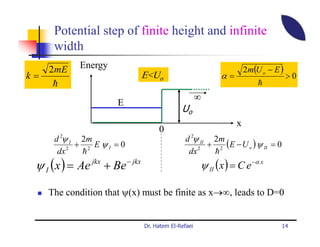
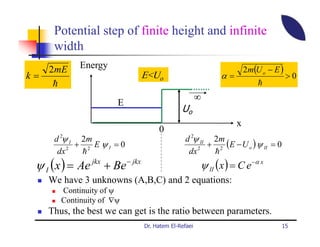
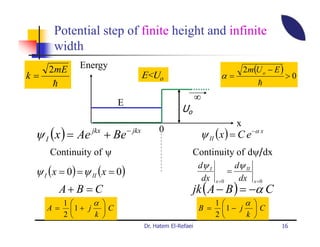
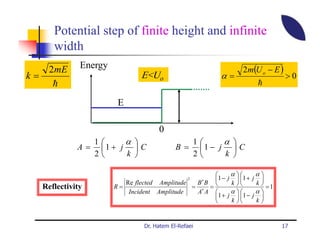
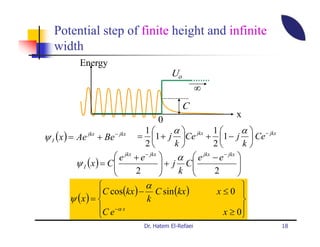
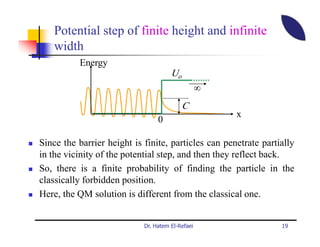
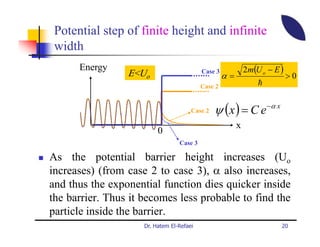
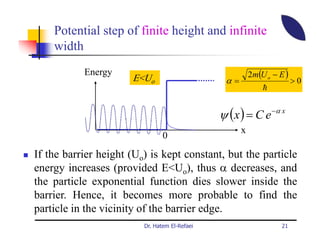
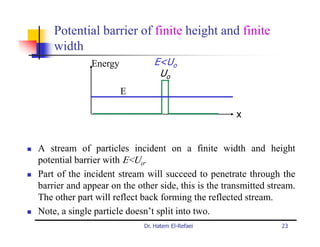
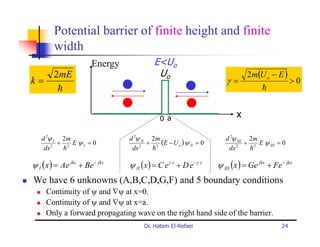
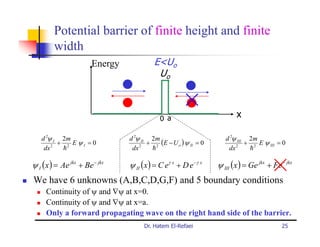
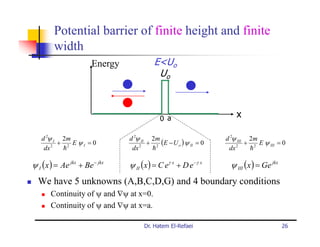
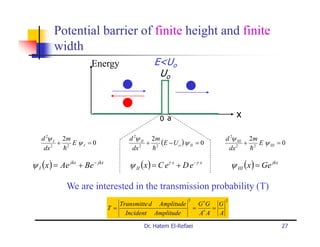
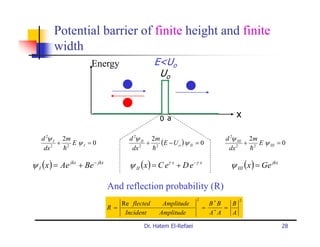
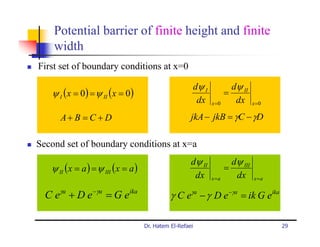
This document summarizes a lecture on modern physics and quantum mechanics. It discusses infinite potential barriers, finite potential barriers, and quantum tunneling. For an infinite barrier, particles reflect completely. For a finite barrier, particles can partially penetrate the barrier due to quantum tunneling, with probability of penetration decreasing as the barrier height or width increases.







![Potential barrier of finite height and finite
width
A+ B = C + D (1)
jkA − jkB = γC − γD (2)
γa −γa (3)
C e +De =Ge ika
γ C eγa − γ D e −γa = ik G eika (4)
Eq. (1) × jk + Eq. (2) to eliminate B
2 jkA = ( jk + γ )C + ( jk − γ ) D (7)
Substitute from eq. (5) and (6) into (7), we get an equation of A
and G only.
2 jkA =
1
2γ
[ ]
(γ + jk )2 e( jk −γ )a − (γ − jk )2 e( jk +γ )a G (8)
hatem@oilpeakinarabic.org Dr. Hatem El-Refaei 31](https://image.slidesharecdn.com/physics-barriersandtunneling-121210083719-phpapp02/85/Physics-barriers-and-tunneling-32-320.jpg)











![Potential barrier of finite height and finite
width
A+ B = C + D (1)
jkA − jkB = γC − γD (2)
γa −γa (3)
C e +De =Ge ika
γa − γa
γ C e − γ D e = ik G e ika (4)
Eq. (1) × jk + Eq. (2) to eliminate B
2 jkA = ( jk + γ )C + ( jk − γ ) D (7)
Substitute from eq. (5) and (6) into (7), we get an equation of A
and G only.
2 jkA =
1
2γ
[ ]
(γ + jk )2 e( jk −γ )a − (γ − jk )2 e( jk +γ )a G (8)
Dr. Hatem El-Refaei 31](https://image.slidesharecdn.com/physics-barriersandtunneling-121210083719-phpapp02/85/Physics-barriers-and-tunneling-71-320.jpg)