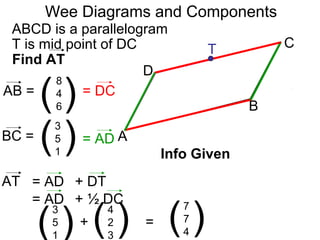
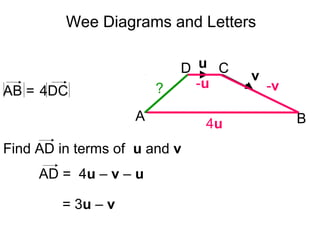
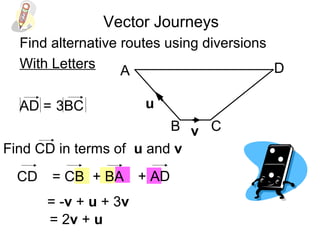
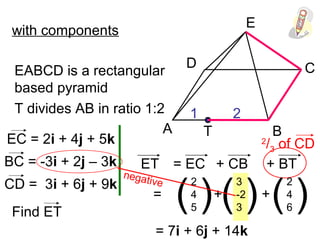
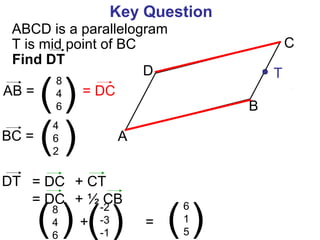
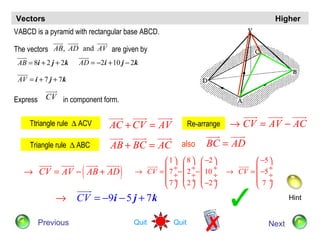
The document discusses vectors and their components. It provides examples of finding the components of vectors using other known vectors, such as finding the components of vector AC given the components of vectors AB and BC. It also discusses using the triangle rule to find unknown vectors. Diagrams are included to illustrate different vector problems and solutions.

1. Block 3
Vector Journeys

2. What is to be learned?
• How to get components of a vector using
other vectors

3. Useful (Indeed Vital!) To Know
Parallel vectors with the same magnitude will
have the same…………………
If vector AB has components ai + bj + ck,
then BA will have components……………...
components
-ai – bj – ck

4. Diversions
Sometimes need
alternative route!
A
B
C
D
E
AE = AB + BC + CD + DE

5. Diversions
Sometimes need
alternative route!
A
B
C
D
E
AE = AB + BC + CD + DE

6. Diversions
Sometimes need
alternative route!
A
B
C
D
E
AE = AB + BC + CD + DE

7. Diversions
Sometimes need
alternative route!
A
B
C
D
E
AE = AB + BC + CD + DE

8. Using Components
AB = 2i + 4j + 5k and BC = 5i + 8j + 3k
AC
= 7i + 12j + 8k
DE = 6i + 5j + k and FE = -3i + 4j + 5k
DF
= 9i + j – 4k
= AB + BC
= DE + EF
= 3i – 4j – 5k
EF

9. Wee Diagrams and Components
A
B
C
D
ABCD is a parallelogram
TT is mid point of DC
AB =
8
4
6( )
BC =
3
5
1
( )
AT
Info Given
= DC
= AD
= AD + DT
= AD + ½ DC
3
5
1( )
4
2
3
( )+
7
7
4
( )=
Find AT

10. Wee Diagrams and Letters
A B
CD
AB = 4DC
u
v
Find AD in terms of u and v
?
4u
-v-u
AD = 4u – v – u
= 3u – v

11. Vector Journeys
Find alternative routes using diversions
With Letters A
B C
D
u
v
AD = 3BC
Find CD in terms of u and v
CD = CB + BA + AD
= -v + u + 3v
= 2v + u

12. with components
A B
CD
E
EABCD is a rectangular
based pyramid
T
T divides AB in ratio 1:2
EC = 2i + 4j + 5k
BC = -3i + 2j – 3k
CD = 3i + 6j + 9k
Find ET
ET = EC + CB + BT
2
/3 of CD
1 2
2
4
5( )=
3
-2
3( )+ +
negative 2
4
6( )
= 7i + 6j + 14k

13. Key Question
A
B
C
D
ABCD is a parallelogram
T
T is mid point of BC
AB =
8
4
6( )
BC =
4
6
2
( )
DT
= DC
= DC + CT
= DC + ½ CB
8
4
6
( )
-2
-3
-1( )+
6
1
5( )=
Find DT

14. Questions
Cunningly Acquired!

17. Hint
QuitQuit
Vectors Higher
Previous Next
VABCD is a pyramid with rectangular base ABCD.
The vectors are given by
Express in component form.
, andAB AD AV
uuur uuur uuur
8 2 2AB = + +
uuur
i j k 2 10 2AD = − + −
uuur
i j k
7 7AV = + +
uuur
i j k
CV
uuur
AC CV AV+ =
uuur uuur uuur
CV AV AC→ = −
uuur uuur uuur
BC AD=
uuur uuur
AB BC AC+ =
uuur uuur uuur
Ttriangle rule ∆ ACV Re-arrange
Triangle rule ∆ ABC also
( )CV AV AB AD→ = − +
uuur uuur uuur uuur 1 8 2
7 2 10
7 2 2
CV
−     
 ÷  ÷  ÷
→ = − − ÷  ÷  ÷
 ÷  ÷  ÷−     
uuur
5
5
7
CV
− 
 ÷
→ = − ÷
 ÷
 
uuur
9 5 7CV = − +→ −
uuur
i j k

18. VECTORS: Question 3
Go to full solution
Go to Marker’s Comments
Go to Vectors Menu
Reveal answer only
EXIT
P
Q
R
S
T
U V
W
A
B
PQRSTUVW is a cuboid in which
PQ , PS & PW are represented by the
vectors
→ → →
[ ],
4
2
0
[ ]and
-2
4
0
[ ]resp.
0
0
9
A is 1
/3 of the way up ST & B is the
midpoint of UV.
ie SA:AT = 1:2 & VB:BU = 1:1.
Find the components of PA & PB and hence the size of angle APB.
→ →

19. VECTORS: Question 3
Go to full solution
Go to Marker’s Comments
Go to Vectors Menu
Reveal answer only
EXIT
P
Q
R
S
T
U V
W
A
B
PQRSTUVW is a cuboid in which
PQ , PS & PW are represented by the
vectors
→ → →
[ ],
4
2
0
[ ]and
-2
4
0
[ ]resp.
0
0
9
A is 1
/3 of the way up ST & B is the
midpoint of UV.
ie SA:AT = 1:2 & VB:BU = 1:1.
Find the components of PA & PB and hence the size of angle APB.
→ →
|PA|
→
= √29
|PB|
→
= √106
= 48.1°APB

20. Markers Comments
Begin Solution
Continue Solution
Question 3
Vectors Menu
Back to Home
PA =
→
PS + SA =
→ →
PS + 1
/3ST
→→
PS + 1
/3PW
→→
=
[ ]
-2
4
0
[ ] =
0
0
3
+ [ ]
-2
4
3
=
PB =
→
PQ + QV + VB
→ → →
PQ + PW + 1
/2PS
→ → →
=
[ ]
4
2
0
[ ]+
0
0
9
+ [ ]=
-1
2
0
[ ]
3
4
9
=
PQRSTUVW is a cuboid in which
PQ , PS & PW are represented by
vectors
→ → →
[ ],
4
2
0
[ ]and
-2
4
0
[ ]resp.
0
0
9
A is 1
/3 of the way up ST & B is the
midpoint of UV.
ie SA:AT = 1:2 & VB:BU = 1:1.
Find the components of PA & PB
and hence the size of angle APB.
→ →

21. Markers Comments
Begin Solution
Continue Solution
Question 3
Vectors Menu
Back to Home
PA =
→
[ ]
-2
4
3
PB =
→
[ ]
3
4
9PQRSTUVW is a cuboid in which
PQ , PS & PW are represented by
vectors
→ → →
[ ],
4
2
0
[ ]and
-2
4
0
[ ]resp.
0
0
9
A is 1
/3 of the way up ST & B is the
midpoint of UV.
ie SA:AT = 1:2 & VB:BU = 1:1.
Find the components of PA & PB
and hence the size of angle APB.
→ →
(b) Let angle APB = θ
θ
A
P
B
ie
PA .
→
PB =
→
[ ]
-2
4
3
[ ]
3
4
9
.
= (-2 X 3) + (4 X 4) + (3 X 9)
= -6 + 16 + 27
= 37

22. Markers Comments
Begin Solution
Continue Solution
Question 3
Vectors Menu
Back to Home
PQRSTUVW is a cuboid in which
PQ , PS & PW are represented by
vectors
→ → →
[ ],
4
2
0
[ ]and
-2
4
0
[ ]resp.
0
0
9
A is 1
/3 of the way up ST & B is the
midpoint of UV.
ie SA:AT = 1:2 & VB:BU = 1:1.
Find the components of PA & PB
and hence the size of angle APB.
→ →
PA .
→
PB =
→
37
|PA| = √((-2)2
+ 42
+ 32
)
→
= √29
|PB| = √(32
+ 42
+ 92
)
→
= √106
Given that PA.PB = |PA||PB|cosθ
→ →
then cosθ =
PA.PB
→ →
|PA||PB|
=
37
√29 √106
so θ = cos-1
(37 ÷ √29 ÷ √106)
= 48.1°

23. Ex
Suppose that AB = ( )3
-1 and BC = ( ) .5
8
Find the components of AC .
AC = AB + BC =
********
( ) + ( )3
-1
5
8 = ( ) .8
7
Ex
Simplify PQ - RQ
********
PQ - RQ = PQ + QR = PR