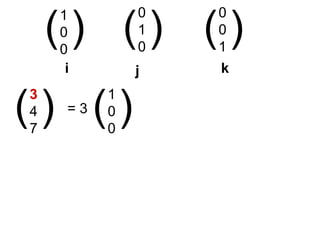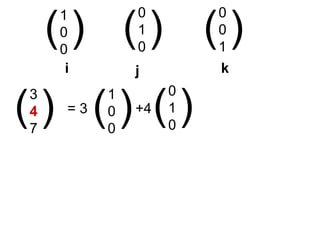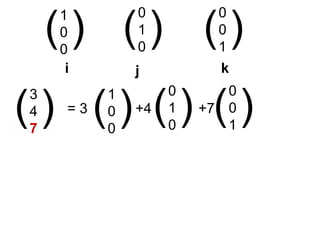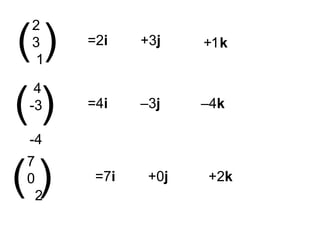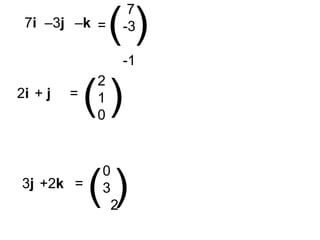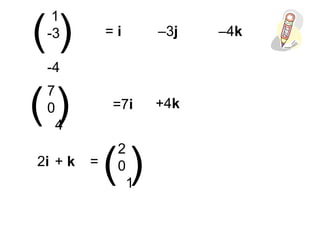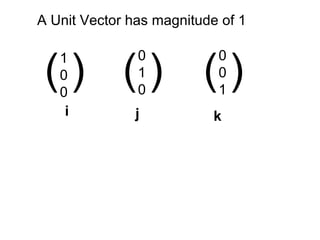
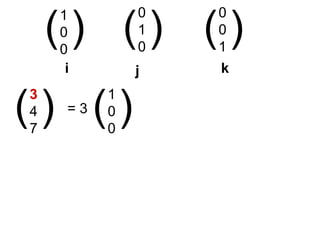
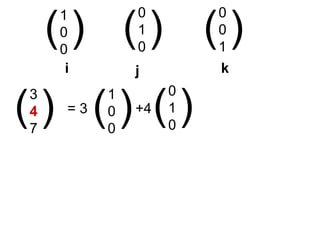
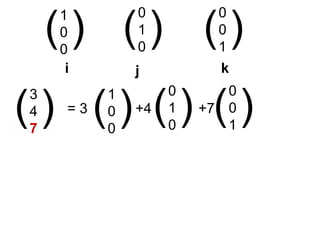
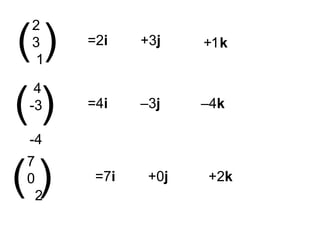
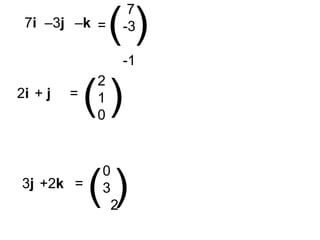
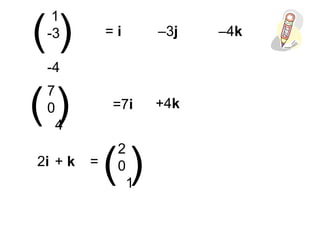
This document introduces unit vectors and how they can be used to write the components of a vector. It defines a unit vector as having a magnitude of 1 and lists the standard unit vectors i, j, k. It then shows how any vector can be written as the sum of its components in the direction of each unit vector, using examples like 3i + 4j + 7k. Finally, it provides additional examples of writing vectors in component form using unit vectors and calculating the sum of two vectors.

1. Block 3
Unit Vectors
and Components

2. What is to be learned?
• What a unit vector is
• How to use unit vectors to write
components

3. A Unit Vector has magnitude of 1
1
0
0
0
1
0
0
0
1
( )
i j k
( ) ( )

4. 1
0
0
0
1
0
0
0
1
( )
i j k
( ) ( )
3
4
7
( ) 1
0
0
( )= 3

5. 1
0
0
0
1
0
0
0
1
( )
i j k
( ) ( )
3
4
7
( ) 1
0
0
( )= 3
0
1
0
( )+4

6. 1
0
0
0
1
0
0
0
1
( )
i j k
( ) ( )
3
4
7
( ) 1
0
0
( )= 3
0
1
0
( )+4
0
0
1
( )+7

7. 1
0
0
0
1
0
0
0
1
( )
i j k
( ) ( )
3
4
7
( ) 1
0
0
( )= 3
0
1
0
( )+4
0
0
1
( )+7
3i +4j +7k

8. 2
3
1
( ) =2i +3j + k
4
-3
-4
( ) =4i –3j –4k
7
0
2
( )
1
=7i +0j +2k

9. 7
-3
-1
( )7i –3j –k
0
3
2
( )3j +2k
=
=
2
1
0
( )2i + j =

10. Unit Vectors and Components
Gives us another way to write components
Unit Vectors have a magnitude of 1
1
0
0
0
1
0
0
0
1
( )
i j k
( ) ( )

11. 1
-3
-4
( ) = i –3j –4k
7
0
4
( ) =7i +4k
2
0
1
( )2i + k =

12. If a = 3i – 4j + k , write a in component form,
then calculate 2a
3
-4
1
a =
( )
6
-8
2
2a =
( )
2a = √(62
+ (-8)2
+ 22
)
= √104
Key Question